基于BBM非飽和土本構模型的高填路堤沉降特性

關振長，毛順飛，張淑寶，徐惠明

(1.福州大學 土木工程學院，福建 福州 350116; 2.漳州廈蓉高速擴建工程有限公司, 福建 漳州 363000)

0 引言

隨著我國高速公路建設向山嶺重丘地區發展，高填路堤因其建設成本低、施工難度小，且能有效利用挖方棄土等優點，而被廣泛運用。而控制高填路堤的沉降量、保證高填路堤的穩定性，是保證其工程建設質量與安全的關鍵所在。

許多學者采用數值模擬方法對高填路堤沉降特性展開了相關研究。楊靜[1]依托新疆某高速公路工程，在ABAQUS數值平臺上采用MC本構模型分析了路基拓寬對其沉降的影響，結果表明拓寬后最大豎向位移呈倒鐘形分布，主要出現在新路基一側。鄭建斌[2]在Geostudio平臺上采用MC本構模型對軟土地區路基沉降進行數值模擬研究，結果表明地基回彈模量對路基沉降有很大的影響，路基頂面沉降值隨地基回彈模量的增大而減小。李自強[3]在ABAQUS數值平臺上采用MCC本構模型對深厚軟土區的沉降問題展開研究，結果表明由于防護堤沉降量過大，將會影響其上部建構筑物安全，建議在防護堤施工前進行地基處理。占鑫杰[4]依托連云港淤泥地基工程實例，在FLAC3D數值平臺上采用MCC本構模型分析了不同涂抹效應參數對地基表面沉降的影響，結果表明當涂抹區滲透系數減小，涂抹半徑增大時，地基固結沉降速率變緩。

綜上所述，目前基于數值模擬的路堤沉降特性分析，大多采用MC,MCC等常規本構模型[5-7]，僅能考慮完全飽和或完全干燥的情況。但實際上高填路堤所用填料多為非飽和土，常規本構模型未考慮非飽和土中基質吸力的影響，其計算分析結果不夠準確。因此，以廈蓉高速公路漳州段高填路堤工程為背景，基于BBM非飽和土本構模型，在FLAC3D數值平臺上分析其沉降變形，并與常規MCC本構模型的計算結果相比照，為高填路堤沉降特性的研究提供參考。

1 MCC本構模型

英國劍橋大學Roscoe和Schofield[8]于20世紀中葉，在對正常固結黏土和弱超固結黏土進行大量三軸試驗的基礎上，提出了一種等向硬化的彈塑性本構模型，稱之為修正劍橋(MCC)本構模型。其核心是提出了臨界狀態線和狀態邊界面的概念。該模型通過等向三軸壓縮試驗和常規三軸壓縮試驗，采用相關聯流動法則建立起屈服函數f(σ)和勢函數g(σ)的數學方程式。20世紀60年代末，Burland教授進一步引入彈性偏應變不為0的修正，并使其屈服函數得以完善，在p-q坐標系中其屈服面呈橢圓狀，在主應力空間中則為橢球狀體。

由各向等壓固結試驗(即q=0情況)可得到孔隙比e與平均應力p之間的關系。以比體積v為縱坐標，lnp為橫坐標，繪制如圖1所示固結曲線。該曲線稱之為正常固結線，簡稱NCL，其中AB為壓縮固結曲線，CD為回彈再壓縮曲線，λ,κ分別為加載、卸載曲線的斜率。

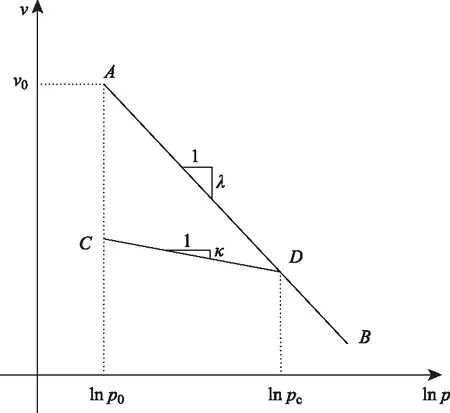
圖1 v-ln p固結曲線Fig.1 v-ln p consolidation curve

Roscoe通過常規三軸壓縮試驗證明，無論是排水剪切、不排水剪切或其他任何應力路徑試驗都具有相同的破壞軌跡(即臨界破壞線CSL)，在p-q平面上是一條過原點的直線，如圖2所示。臨界破壞線CSL的表達式為q=Mp，其中M為該直線的斜率，也稱為臨界狀態有效應力比。橢圓型屈服曲線為土體從開始受剪直到破壞的屈服軌跡，每一個確定的p值對應一條屈服軌跡；其最大屈服軌跡的水平半軸為pc/2，豎向半軸為Mpc/2，橢圓中心在(pc/2，0)位置。

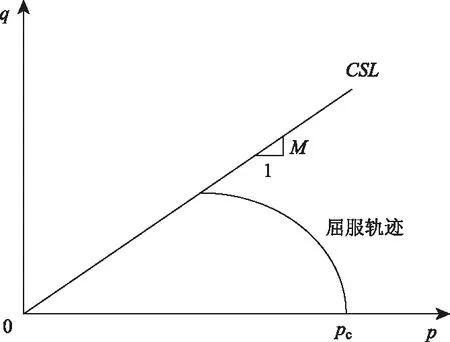
圖2 p-q平面上的屈服軌跡Fig.2 Yield trajectory in p-q plane

進一步地，以p，v，q為坐標建立三維空間，將土體三軸試驗破壞時的p-q-v對應關系描繪在三維空間中，該關系唯一且表示為一條空間曲線，其在p-q面上的投影即為CSL線，該曲線稱之為空間臨界狀態線。由空間臨界狀態線，v-p平面NCL線，p-q平面屈服軌跡以及v軸所圍成的空間曲面既表示土體狀態邊界面。該曲面以下為彈性區，以上不可達到，故可根據p-q-v關系所處位置作為判別是否屈服的標準，并由此建立相應的屈服準則。

MCC本構模型是目前巖土工程界廣泛應用的彈塑性本構模型之一，其參數λ，κ，pc，M，μ，G,p0和v0都具有明確的物理意義，且容易由常規土工試驗獲取，詳見表1。

2 BBM非飽和本構模型

基于臨界狀態理論建立的MCC本構模型標志著現代土力學理論的發端，被廣泛應用于各類土工計算中。但該本構主要是針對飽和土而建立的，而實際工程中遇到的土體大多處于非飽和狀態，黃土、膨脹土、殘積土、人工填土以及地下水位以上的土，都是典型的非飽和土。基質吸力s的存在是非飽和土區別于飽和土的重要原因，因此如何考慮基質吸力的影響，是建立非飽和土本構模型的關鍵所在。

表1 MCC本構模型參數Tab.1 Parameters for MCC constitutive model

2.1 BBM本構模型及其參數

Alonso[9]等基于試驗結果提出不同吸力下非飽和土體積變化與應力的關系，并將此變化融入到修正劍橋模型中，于20世紀90年代建立了BBM非飽和土本構模型[10]。與其他彈塑性本構模型一樣，BBM本構模型也將土體變形分為彈性變形和塑性變形，采用平均凈應力p，偏應力q，基質吸力s這3種應力變量，在應力空間中以屈服面(SI，LC，CSL)來劃分彈性空間與塑性空間。

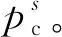
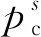
(1)

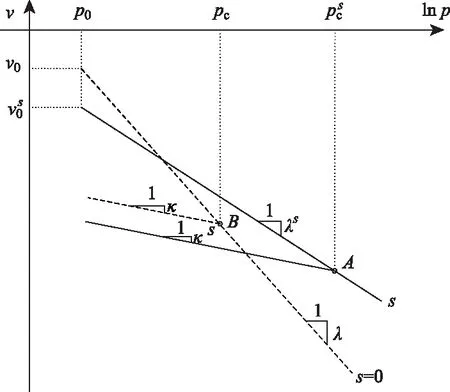
圖3 飽和與非飽和土的壓縮曲線Fig.3 Compression curves of saturated and unsaturated soils

式中λs隨基質吸力s變化的經驗公式為：

λs=λ[(1-r)exp(-βs)+r],

(2)

式中,r為與土體最大剛度有關的常數;β為控制土體剛度λ隨基質吸力s增長速率的參數。

當吸力ssc時，土體將產生塑性變形。sc為屈服與否的分界點，其實際意義與最大先期固結應力相似，為土體應力歷史上的最大吸力值。將其繪在p-s平面內，為一條水平線，稱之為SI(suction-increase)屈服曲線，相應的屈服函數為：

s=sc。

(3)

LC和SI屈服曲線在p-s平面上如圖4所示。

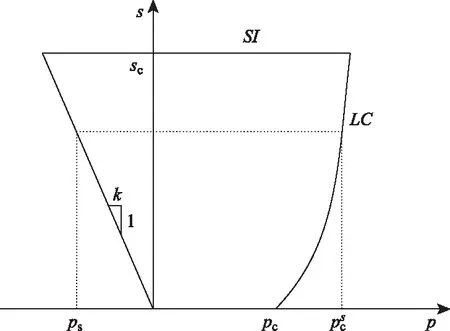
圖4 p-s平面上的屈服線Fig.4 Yield curve on p-s plane

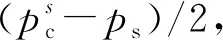
圖5 空間屈服面在p-q平面上的投影Fig.5 Projection of spatial yield surface on p-q plane

BBM模型基于飽和土臨界狀態概念和增量塑性理論，能較好地反映非飽和土的主要應力-應變特征，其所需參數及物理意義如表2所示。

表2 BBM本構模型參數Tab.2 Parameters for BBM constitutive model

2.2 基質吸力的成因及確定方法

非飽和土與飽和土的主要區別在于土中存在第三相，即氣相[12]。嚴格來說非飽和土中的水與氣體的分界面，由于其性質的特殊性應被視為另一獨立的相，稱為收縮膜。正是由于收縮膜的存在，土中水可以有不同的應力值。與大氣接觸處的水壓為0，而與收縮膜彎液面接觸處的水壓小于氣接觸處，即土中孔隙水壓力uw為負值，說明土中水是處于承受拉應力的狀態。彎液面兩邊孔隙氣壓力ua大于孔隙水壓力uw，一般情況下孔隙氣壓力等于大氣壓，而ua與uw的差值稱為基質吸力s[13]。

基質吸力反映以土的結構、土粒成分、孔隙分布形態等土的基質對土中水的吸持作用。基質吸力隨土中含水量增加而降低，飽和土體所有孔隙已被水占據而沒有吸水能力，即基質吸力為零。基質吸力是描述非飽和土力學性質的重要參數，亦是研究BBM本構模型的關鍵所在。常見基質吸力的測試方法包括為直接法和間接法兩大類：其中直接測試方法有壓力板儀法、張力計法、軸平移法；間接測試方法有濕度計法、濾紙法等。土體吸力與含水率間的關系曲線稱之為土水特征曲線(SWCC)，它能夠反映非飽和土的強度、滲透性及持水能力等的基本性質，是研究非飽和土的重要紐帶[14]。

另一方面，基質吸力也可通過理論計算得到，可根據彎液面表面內外差的Young-Laplace公式和彎液面表面蒸氣壓的Kelvin公式，推導出基質吸力的理論計算公式如下[15]：

(4)

式中,ρw為水的密度;T為絕對溫度;pm為T溫度下彎液面的蒸氣壓;p0為T溫度下平液面的蒸氣壓。由式(4)可見，基質吸力與非飽和土中水-氣體系的溫度、孔隙水的密度和孔隙氣的相對濕度有關。

2.3 BBM本構模型數值平臺上的實現

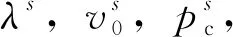
(5)

(6)

(7)

3 高填路堤施工過程的數值模擬

根據BBM非飽和本構模型，在FLAC3D數值平臺上對廈蓉高速公路漳州段高填路堤填筑全過程展開數值模擬，以分析其沉降變形特性。

3.1 工程背景

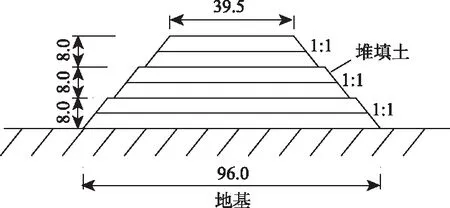
圖6 高填路堤典型設計橫斷面示意圖(單位：m)Tab.6 Schematic diagram of typical designed cross-section of high-filled embankment (unit: m)

廈蓉高速公路漳州段，其線位呈南東-北西向展布，設計速度為80 km/h；雙向8車道，整體式路基寬度39.5 m，單側分離整幅4車道寬度為19.75 m。線路穿越地形起伏、地勢條件復雜、相對高差較大的地段，為解決局部地區棄方量大，達到平衡填挖，沿線設有多處高填路堤段。其典型設計橫斷面示意圖如圖6所示。堆填體高度共24 m，分為3階，每階堆填坡度均為1∶1；每階又分為4層堆填并碾壓密實，每層堆高為2 m。

3.2 數值模型

根據上述典型設計斷面，考慮對稱性，取右半側高填路堤，建立相應的數值模型如圖7所示。原地基及上部堆填體均為六面體實體單元，共計 68 200個單元，67 365個節點。其中原地基橫向邊界取3～5倍路基凈寬，則X方向共計100 m；下部邊界取3～5倍路堤沉降影響范圍，則Z方向共計44 m；Y方向選取目標斷面前后各20 m范圍，共計40 m。邊界條件為：頂面取自由邊界，側面與底面為法向位移約束邊界。

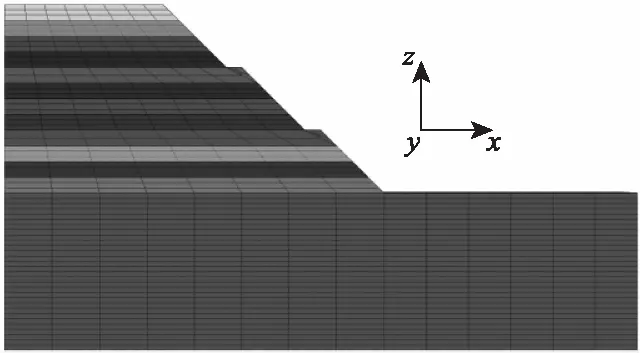
圖7 數值模型網格劃分示意圖Fig.7 Schematic diagram of meshing in numerical model

原地基采用常規摩爾-庫倫(MC)本構模型，堆填體則分別采用BBM或MCC本構模型。依據《工程地質手冊》[18]及廈蓉高速公路(漳州段)設計文件，其本構參數具體取值如表3所示。

3.3 工況與測點

根據高填路堤的施工過程，沿填土高度每2 m堆填并壓實一層，堆填總高度24 m，共計12個工況,如表4所示。同時，在路堤中部沿填土高度每隔4 m布置一個沉降監測點，共計6個監測點，觀察其分層沉降隨施工步的變化規律。

4 高填路堤的沉降特性分析

原地基采用MC本構，堆填體采用BBM非飽和土本構模型，根據數值模擬結果，繪制高填路堤分層沉降隨施工步的變化規律，如圖8所示。

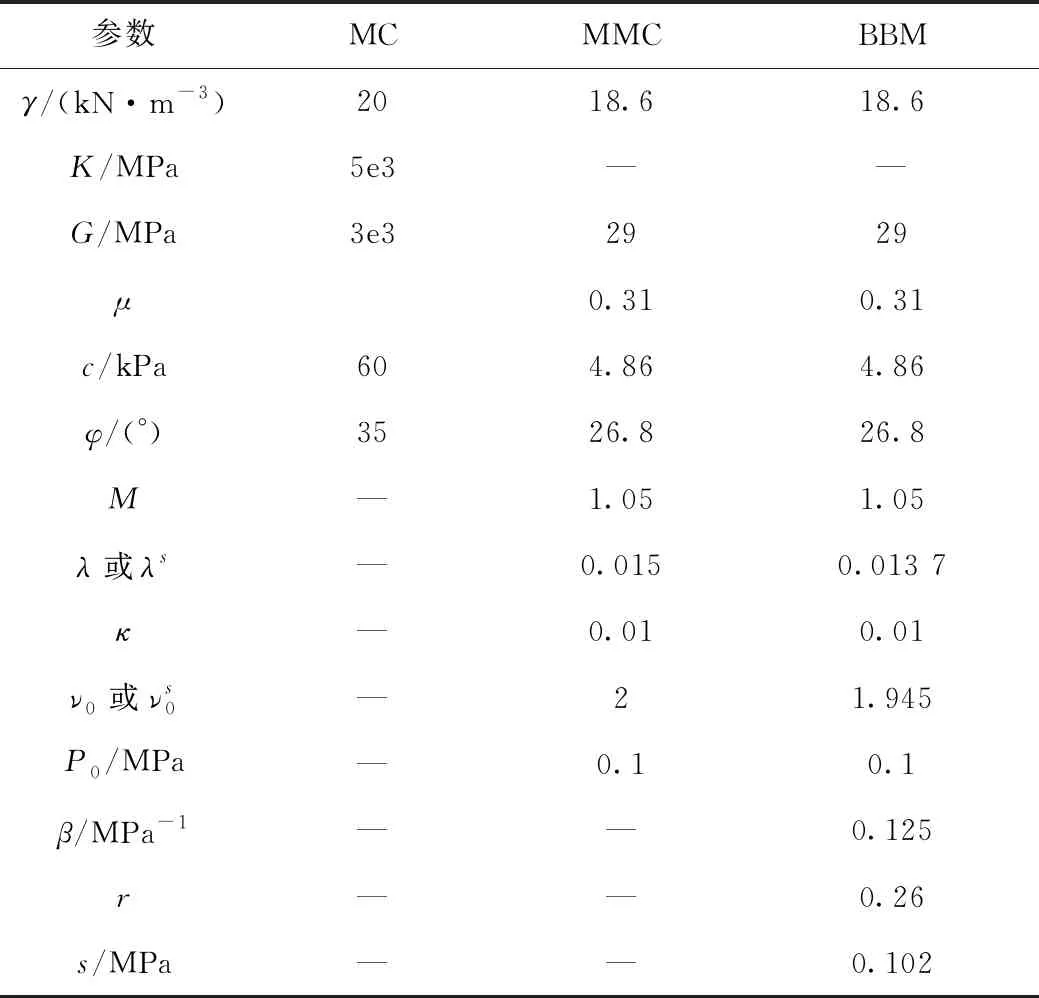
表3 地基與路堤填料的物性參數Tab.3 Physical parameters of foundation and embankment filler

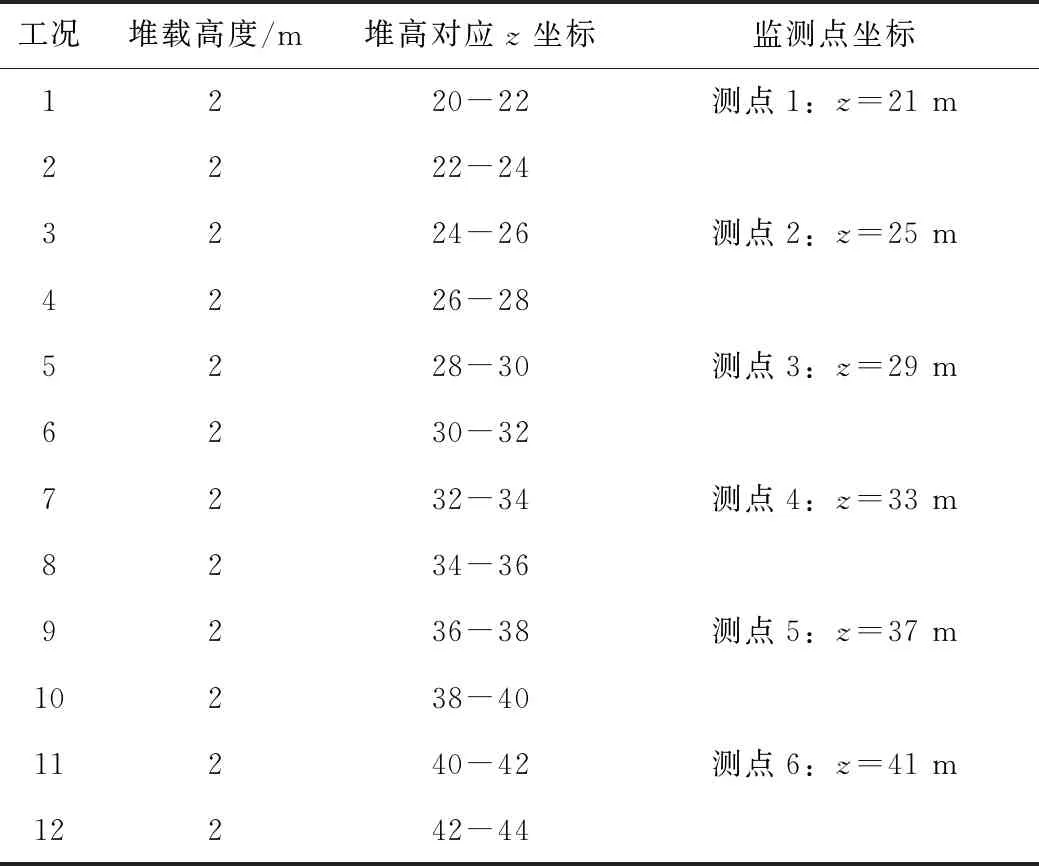
表4 工況及測點位置表Tab.4 Working conditions and measuring point positions

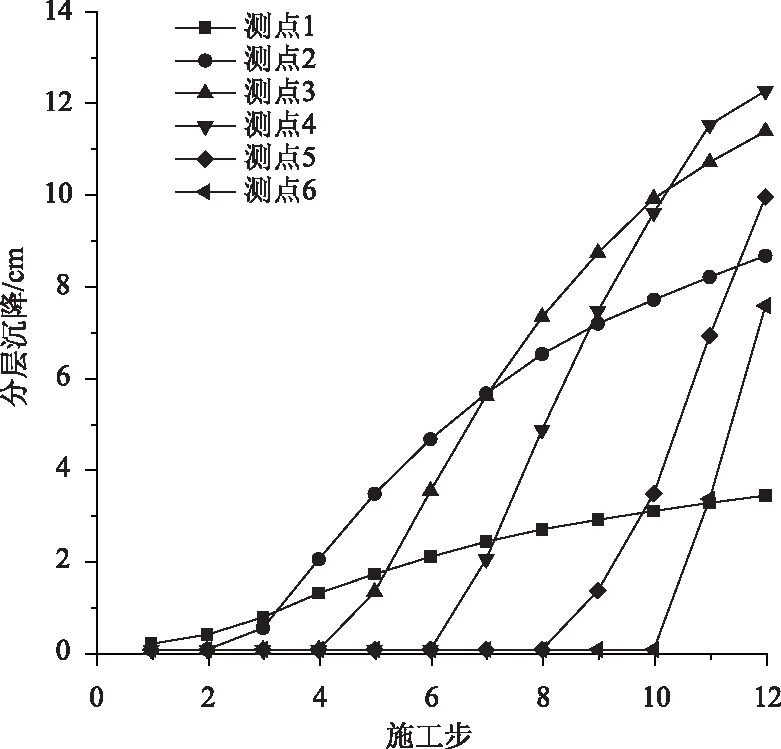
圖8 分層沉降隨施工步的變化規律(BBM本構模型)Fig.8 Stratified settlement varying with construction steps (BBM constitutive model)

首先比較各分層測點沉降的變化率，其變化率從底部(測點1)到頂部(測點6)呈現逐步增大的規律。這說明在相同荷載增量作用下，堆填體分層沉降的變化率與下伏可壓縮層(堆填體自身)的厚度有關，其下伏層越厚，分層沉降變化率越大。

再比較各分層測點的最終沉降量，路堤底部所承受的上覆荷載最大，但其下伏可壓縮層很薄，因此路堤底部(測點1)的分層沉降最小，僅為3.4 cm。同理，路堤頂部雖然下伏可壓縮層較厚，但其承擔的上覆荷載較小，故路堤頂部(測點6)的分層沉降也不大，約為6.9 cm。而路堤中部既承受了較大的上覆荷載，下伏也有較厚的可壓縮層，因此最大分層沉降發生在路堤中部(測點4)，達到12.3 cm。

進一步地繪制各分層測點沉降量沿填土高度的分布規律，如圖9所示。各分層測點的沉降量在高程上呈中間大、兩頭小的規律，且隨著施工步的進行，該規律愈發明顯。上述結論與分層沉降結果相一致，也與李占鋒[19]等的相關研究成果一致。

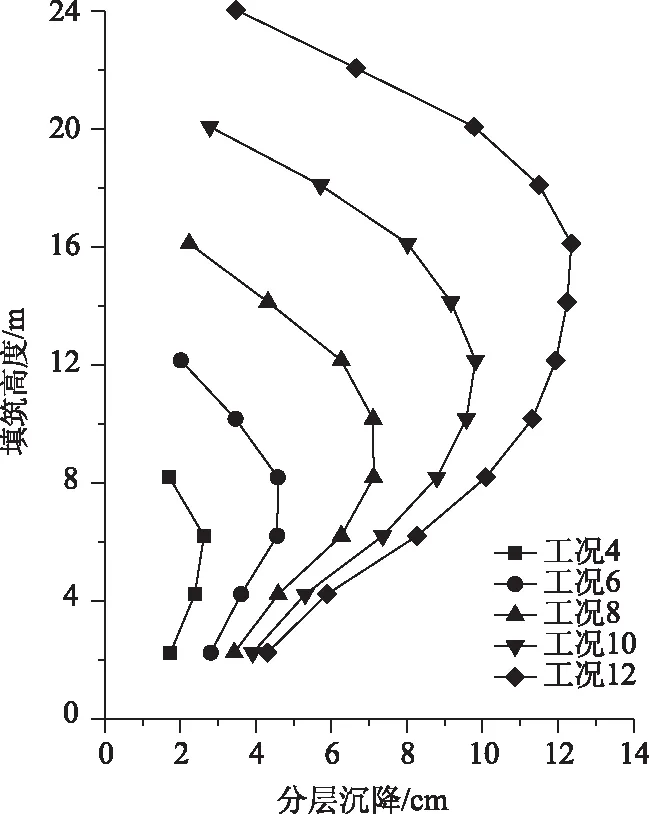
圖9 分層沉降沿高程的分布規律(BBM本構模型)Fig.9 Distribution of stratified settlement along elevation (BBM constitutive model)

5 與MCC模型的對比

原地基仍采用MC本構，堆填體采用MCC飽和土本構模型，根據數值模擬結果，繪制高填路堤分層沉降隨施工步的變化規律，如圖10所示。為了更好體現與前述BBM本構計算結果的區別，圖中僅列出測點1，3，5的分層沉降。

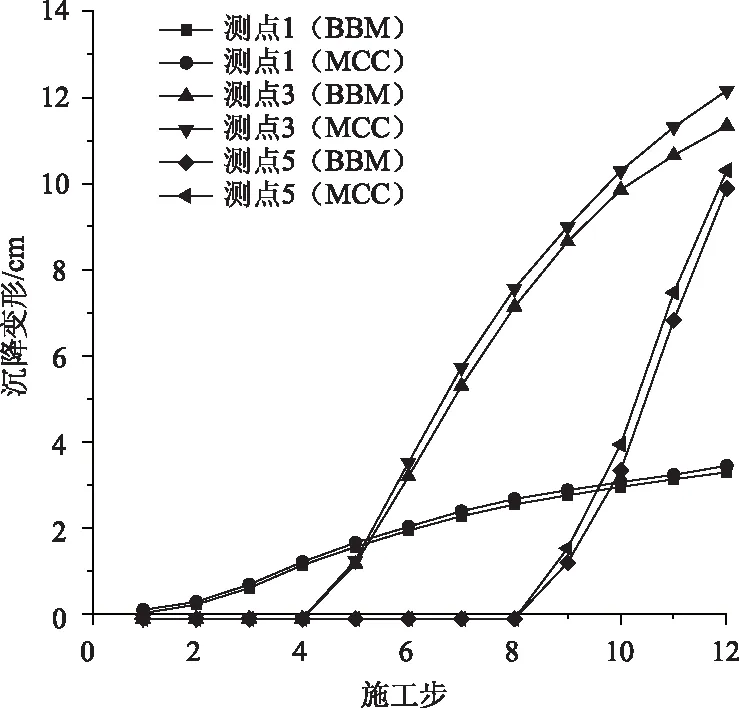
圖10 分層沉降隨施工步的變化規律(MCC與BBM對比)Fig.10 Stratified settlement varying with construction steps (comparison between MCC and BBM)

由圖10可知，采用兩種本構計算所得各測點分層沉降變化規律基本一致。但采用MCC本構計算所得的路堤分層沉降略大，以路堤中部測點3為例，其最終沉降量達到12.1 cm，比采用BBM本構的計算結果(11.2 cm)略大8%。

同樣地，繪制各分層測點沉降量沿填土高度的分布規律，如圖11所示。為了便于與前述BBM本構計算結果進行對比，圖中僅列出工況10和工況12的情形。

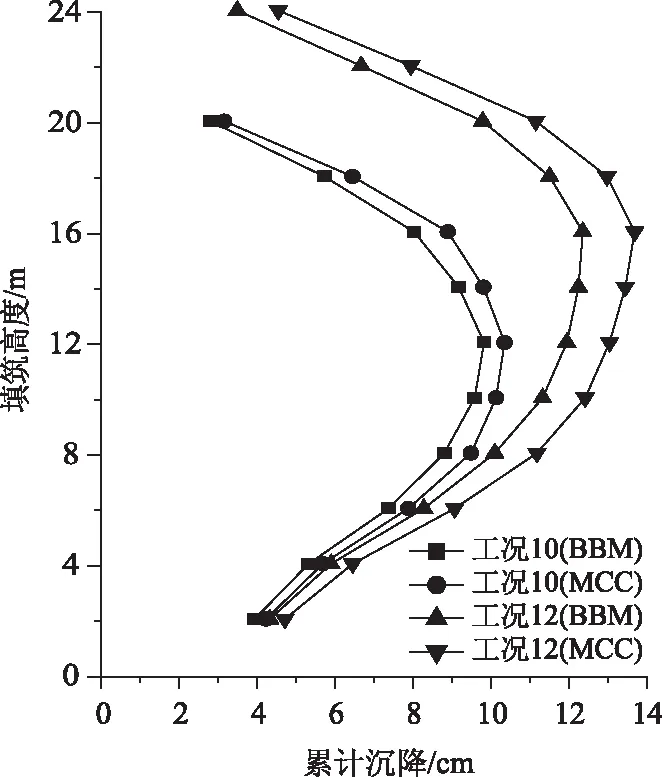
圖11 分層沉降沿高程的分布規律(MCC與BBM對比)Fig.11 Distribution of stratified settlement along elevation (comparison between MCC and BBM)

由上圖可知，采用兩種本構模型計算所得的分層沉降沿填土高度分布規律基本一致，呈現出中間大、兩頭小的規律。但采用MCC本構計算所得的路堤分層沉降整體上均大于前者，以工況12為例，其路堤中部測點4的最終沉降量達到13.7 mm，比采用BBM本構的計算結果(12.3 mm)略大11.4%。

究其原因，BBM本構模型考慮了非飽和土基質吸力s的影響，并通過基質吸力s對飽和土MCC本構中的一些參數(λ，v0，pc)進行修正，使其沉降計算量與分布規律更符合工程實際。上述結果與前人采用飽和與非飽和彈黏塑性本構模型，對高填路堤填筑過程展開數值模擬的結論相一致[20]。

6 結論

以廈蓉高速公路漳州段高填路堤工程為背景，基于BBM非飽和土本構模型，在FLAC3D數值平臺分析了路堤堆填體自身的分層沉降特性。同時與常規MCC飽和土本構模型的計算結果相比照，得到主要結論如下：

(1)無論采用BBM非飽和土本構模型或是MCC飽和土本構模型，其計算所得路堤自身的分層沉降量，均沿填土高度呈現出中間大、兩頭小的分布形態。與底部及上部相比，路堤中部既承受了較大的上覆荷載，也下伏有較厚的可壓縮層，因此最大分層沉降發生在路堤中部。

(2)BBM本構充分考慮了非飽和土基質吸力的影響，并通過基質吸力對MCC本構中的一些參數進行修正，其計算所得沉降量整體上略小于MCC本構的計算結果，其沉降計算量與分布規律更符合工程實際。