基于子空間約束Huber范數的深度域地震子波提取
張 杰 陳學華* 蔣 偉 但志偉 肖 為
(①成都理工大學油氣藏地質及開發工程國家重點實驗室,四川成都 610059; ②成都理工大學地球勘探與信息技術教育部重點實驗室,四川成都 610059; ③中海油田服務公司物探事業部特普公司,廣東湛江 524057)
0 引言
相較于時間域地震資料,深度域地震資料在地質構造復雜的區域能提供更準確的構造信息[1-3]。直接利用深度域地震資料進行屬性分析和反演有助于提高儲層預測和含油氣性檢測精度[4-8],其中準確提取地震子波是關鍵,在很大程度上影響最終反演結果的可靠性。然而,深度域地震波場不滿足“線性時不變”系統的條件,地震子波在不同速度的介質中傳播時,除了受地下介質的衰減、頻散影響,還受介質速度的影響,其波形和延續度均不斷發生變化。因此,如何提取深度域地震子波非常重要。
何惺華[9]利用理論模型和實際資料說明地震子波、褶積和Fourier變換等概念同樣適用于深度域數據。林伯香等[10]指出,深度域中的地震子波是介質速度的函數,其在地下介質的傳播過程不滿足“線性時不變”系統的條件,必須對深度域速度函數進行適當變換,使其滿足由褶積方法計算合成地震記錄的條件。Hu等[11]給出了速度變換的具體方法,為提取深度域地震子波提供了一種思路。所謂速度變換,就是給定一個標準速度,將深度域中各采樣點的速度都調整到該速度,同時深度域中的采樣間隔也要做相應的調整,即等間隔的采樣厚度被相應地“擠壓”或“拉伸”,以保證旅行時不變。速度變換后,將原深度域變為常速度深度域,其采樣間隔不再相等,故還需對常速度深度域的數據進行等間隔的重采樣。在常速度深度域,可以引入褶積模型[11]。因此,可用時間域地震子波提取方法提取常速度深度域地震子波。時間域地震子波提取方法主要有兩類,一是利用地震數據本身的統計信息提取地震子波[12-17],二是利用測井信息和地震數據提取地震子波[18-23],本文主要涉及后者。
在時間域,提取地震子波的時窗長度通常約為子波長度的5~10倍[24]。然而,在常速度深度域,只有數百米深度范圍的可用測井信息,相當于常速度深度域子波長度的2~5倍。因此,在常速度深度域中從“短數據”中提取可靠的地震子波難度較大。此外,還需要考慮數據的截斷效應[16]以提高子波提取精度。為此,本文提出了一種基于子空間約束Huber范數的深度域地震子波提取方法。正演模型測試和實際數據應用結果表明,該方法從有限深度范圍內的數據中提取的地震子波更可靠。
1 方法原理
常速度深度域中的地震記錄為地震子波與反射系數的褶積和噪聲相加的結果,其矩陣形式為
s=Rw+n
(1)
式中:s為包含N個采樣點的地震記錄向量;R為反射系數構建的N×N階矩陣;w為地震子波向量;n為噪聲向量。對于式(1),基于L2范數的求解w的最小二乘法目標函數為
(2)
式(2)的解析解為
(3)
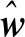
(4)
式中P為N×N階的投影對角矩陣,其結構為
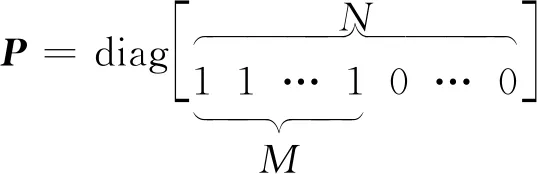
(5)
且P2=P,PT=P。式(4)的解析解為
(6)
實際上,RP的第M+1至第N列元素均為零。因此可用N×M階矩陣Rp替換RP,則式(6)變為
(7)
通過上述子空間約束,不但改善了過擬合現象,還提高了計算效率。然而,由于Rp不是方陣,在矩陣求逆時會出現不穩定現象,可以通過嶺回歸方法
(8)
改善。式中:λ>0為正則化參數,可以通過廣義交叉驗證(generalized cross-validation,GCV)函數確定λ;I為單位矩陣。
由于截斷效應的影響,當計算目標函數時,在數據兩端很容易出現異常值,上述方法易受異常值的影響[25]。此外,確定式(8)的λ也并非易事。一個更穩健的方案是采用基于L1范數的目標函數,但求得的解可能是稀疏的,不適合子波提取。對此,可以考慮結合L1和L2范數——Huber范數的方案[26]。子空間約束Huber范數的目標函數定義為
(9)
其中
(10)
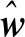
(11)
式中ΦHuber為權重對角矩陣,其對角元素φi定義為
(12)
圖1為L2范數、Huber范數的損失函數和權重函數。由圖可見:當殘差的絕對值大于給定閾值(ε=1)時,Huber范數相當于L1范數;當殘差的絕對值小于給定閾值時,Huber范數相當于L2范數。因此,Huber范數主要對大于閾值的異常值使用小權重處理,以得到更穩健的結果。
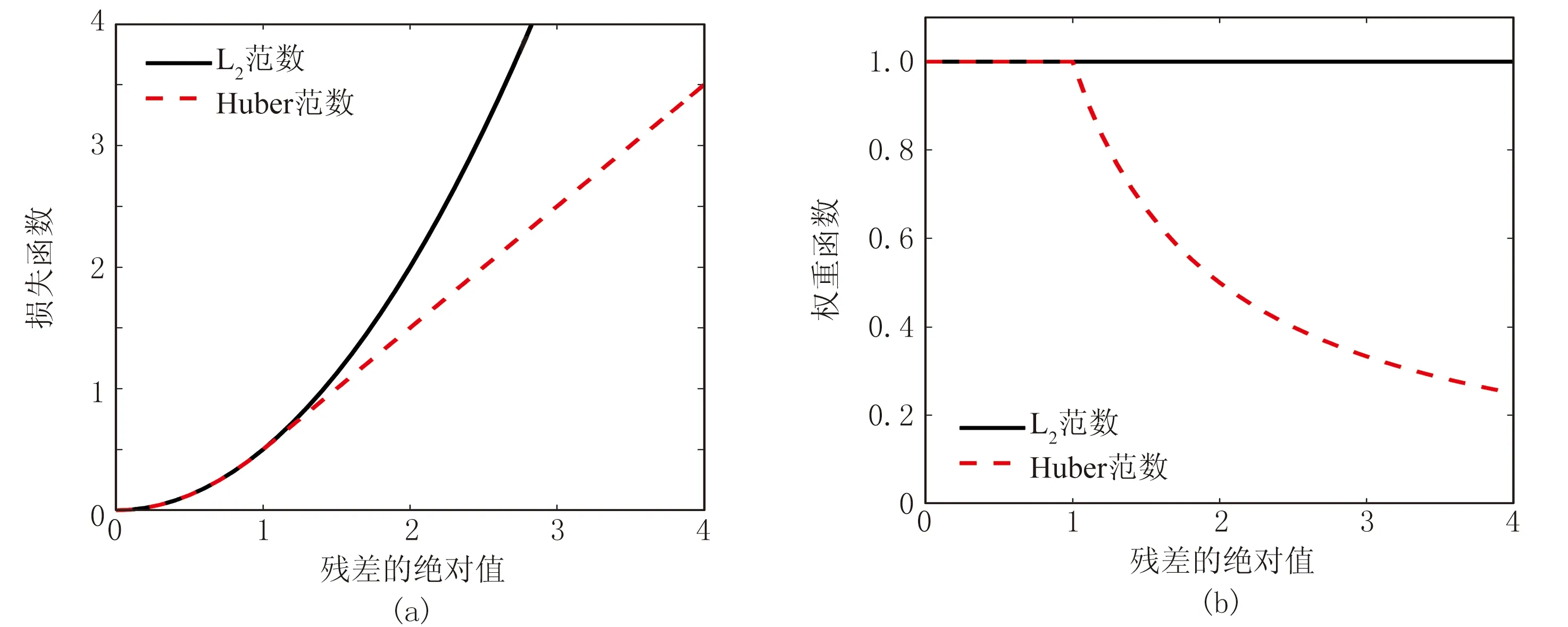
圖1 L2范數與Huber范數的損失函數(a)和權重函數(b)
在使用IRLS求解子空間約束Huber范數的目標函數時,需要給定初始子波和閾值。實際上對初始子波的要求并不高,可以給定一組隨機值或使用最小二乘法的結果。此外,閾值也容易給定,一般取0.0001或0.00001。求解子空間約束Huber范數的目標函數的IRLS算法流程如圖2所示。
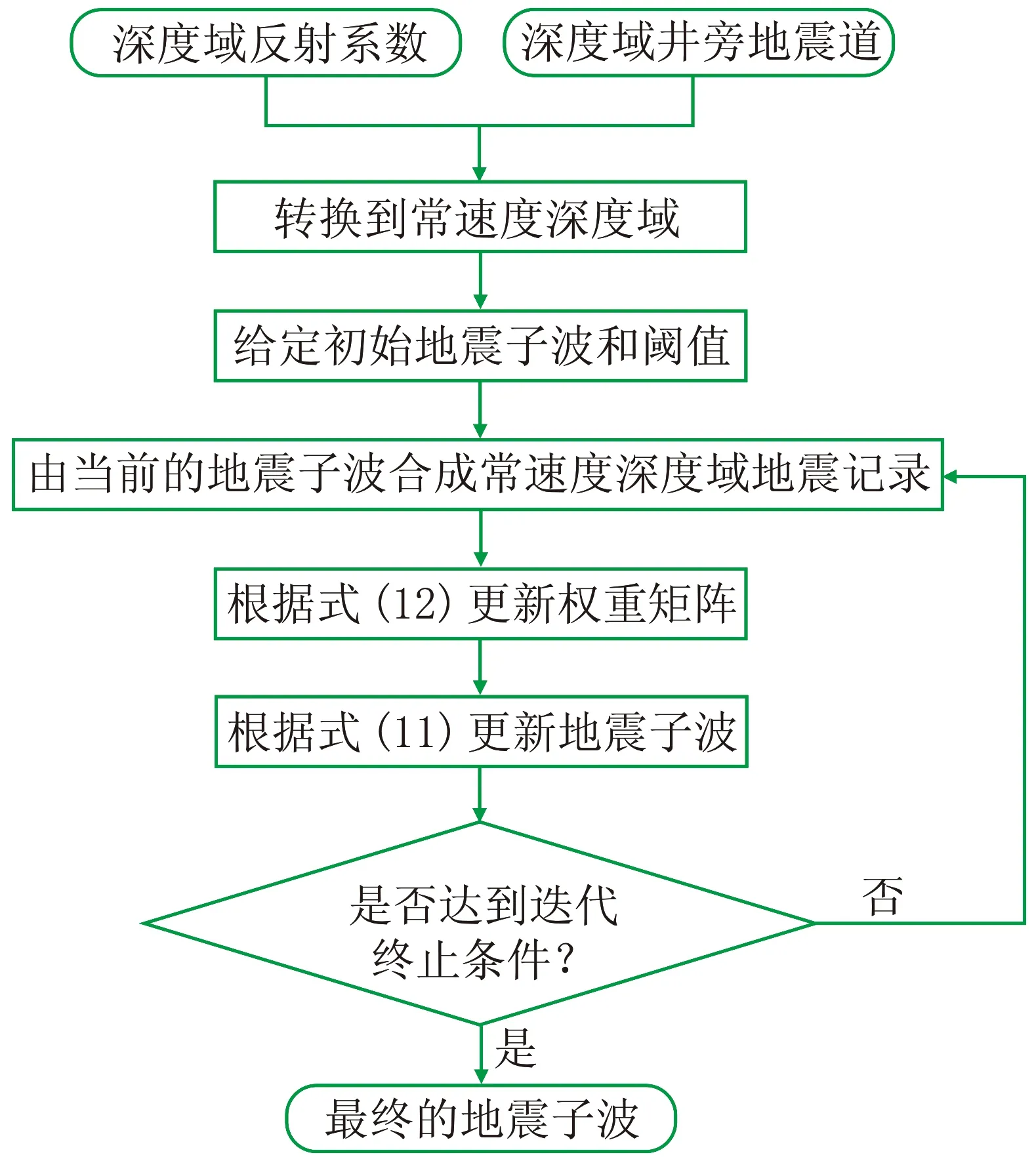
圖2 求解子空間約束Huber范數的目標函數的IRLS算法流程
2 從合成數據中提取地震子波
正演模型(圖3)由實際測井數據和給定的常速度深度域Ricker子波合成。可見:由于給定的常速度小于最大測井速度(圖3b),故對應常速度的深度小于真深度,因此相對于深度域反射系數(圖3c),常速度深度域數據(圖3d、圖3e)被“壓縮”,同樣的現象也出現在實際數據中;常速度深度域Ricker子波含有681個采樣點,對應一個43Hz主頻的時間域Ricker子波(圖3f)。
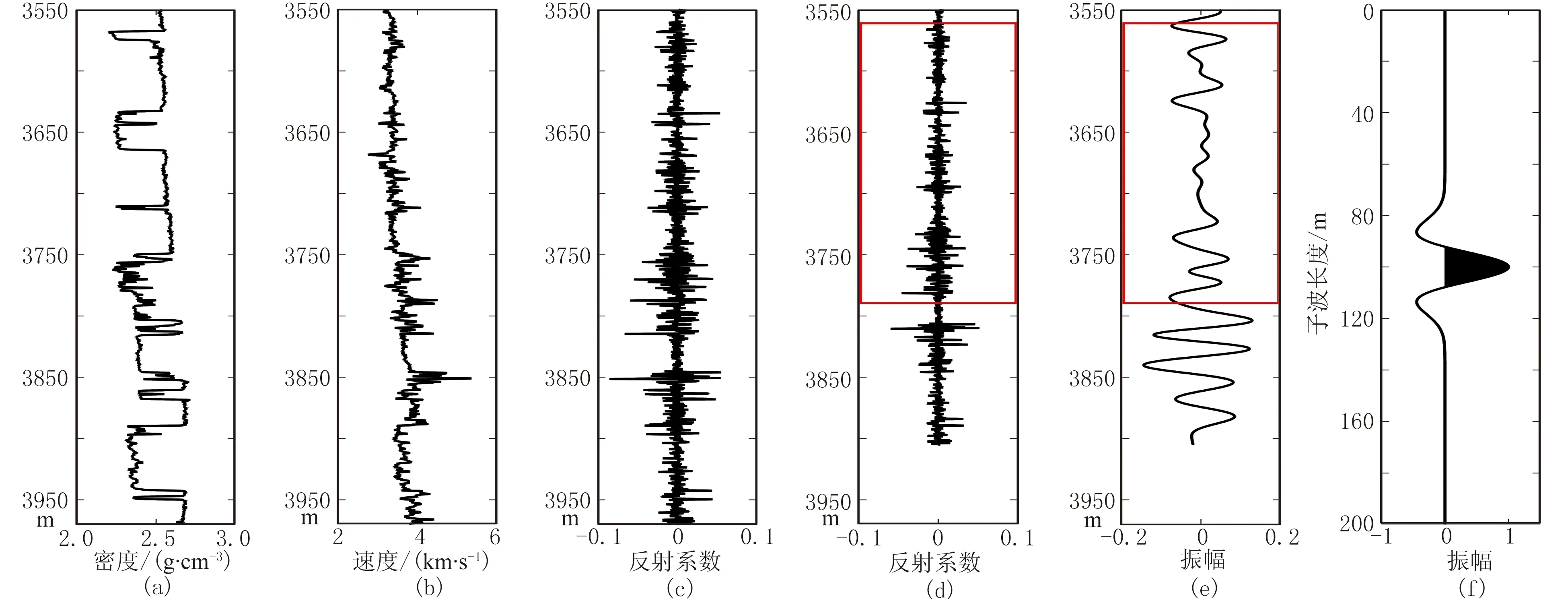
圖3 正演模型
為了測試數據長度對子波提取的影響,分別對不同長度的數據使用本文方法提取地震子波。正演測試中,使用一組隨機數據作為初始子波,設置閾值為0.00001。對不同長度的數據分別進行500次實驗,每次實驗隨機在不同深度位置截取數據并提取子波,由歸一化相關系數(normalized correlation coefficient)NCC和重構質量(reconstruction quality)RQ[29]評價子波提取結果(圖4)。可見,當截取的常速度深度域數據長度與子波長度的比值C≥3時,由本文方法得到的結果較可靠。鑒于此,隨機截取C=3的數據(圖3d、圖3e紅色矩形框中的數據),分別用最小二乘法(least-squares,LS)、子空間約束最小二乘法(subspace-constrained LS,SCLS)、子空間約束嶺回歸方法(subspace-constrained ridge regression,SCRR)和子空間約束Huber范數方法(subspace-constrained Huber norm,SCHN)從該段數據中提取地震子波(圖5),表1為幾種方法的計算時間和評價指標。此外,對每一種方法也分別進行500次隨機實驗,每次實驗在不同深度位置截取C=3的數據提取子波并評價結果(圖6)。需要指出的是,使用子空間約束后,矩陣R的大小由3176×3176減小到2044×681。由圖5、圖6和表1可見,本文方法從較短的數據中提取的地震子波更可靠。因此,若實際數據長度合適,利用該方法還可以提取深變地震子波。

圖4 不同數據長度對地震子波提取的影響
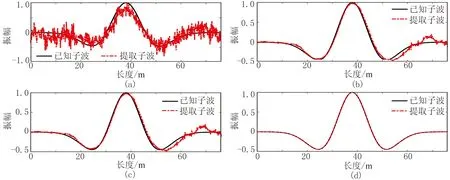
圖5 對同一段數據使用四種方法提取子波的結果
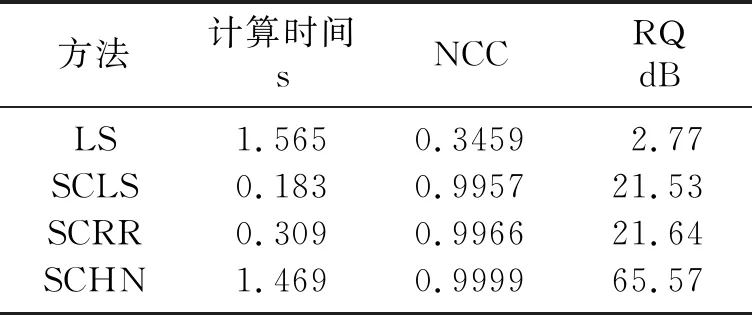
表1 幾種方法的計算時間和評價指標
3 從實際數據中提取地震子波
利用W區的A井、B井的測井數據以及疊前深度偏移地震數據驗證本文方法的有效性。利用不同常速度分別對A井、B井的數據進行速度變換,考慮到數據長度、信噪比、前期數據處理流程等因素,截取C=4的數據提取子波。通過SCLS確定了A井、B井的地震子波長度。將初始子波設定為一組隨機數據,設置閾值為0.0001。圖7、圖8分別為A井、B井測井數據及地震子波提取結果。由圖可見:由提取的地震子波(圖7e、圖8e)合成的深度域地震記錄(圖7b、圖8b中的紅色地震道)與A井、B井的井旁地震道(圖7b、圖8b中的藍色地震道)的相關性很好。
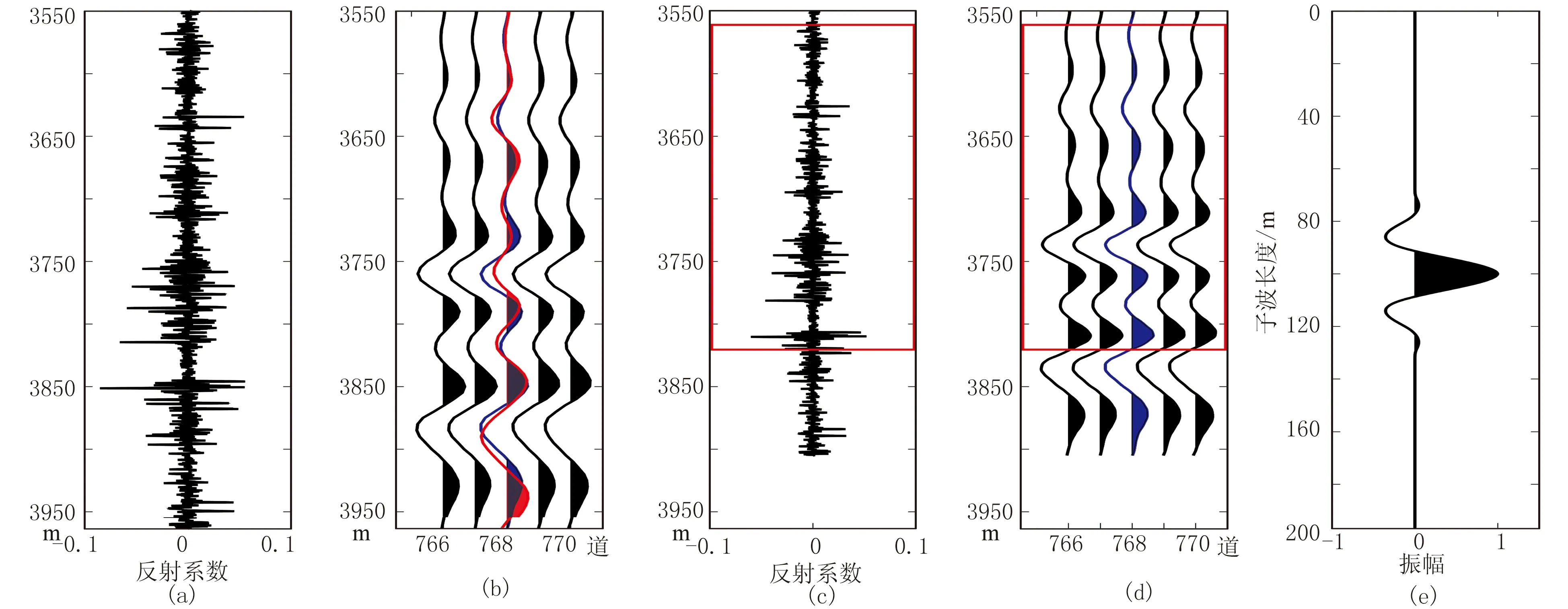
圖7 A井測井數據及地震子波提取結果
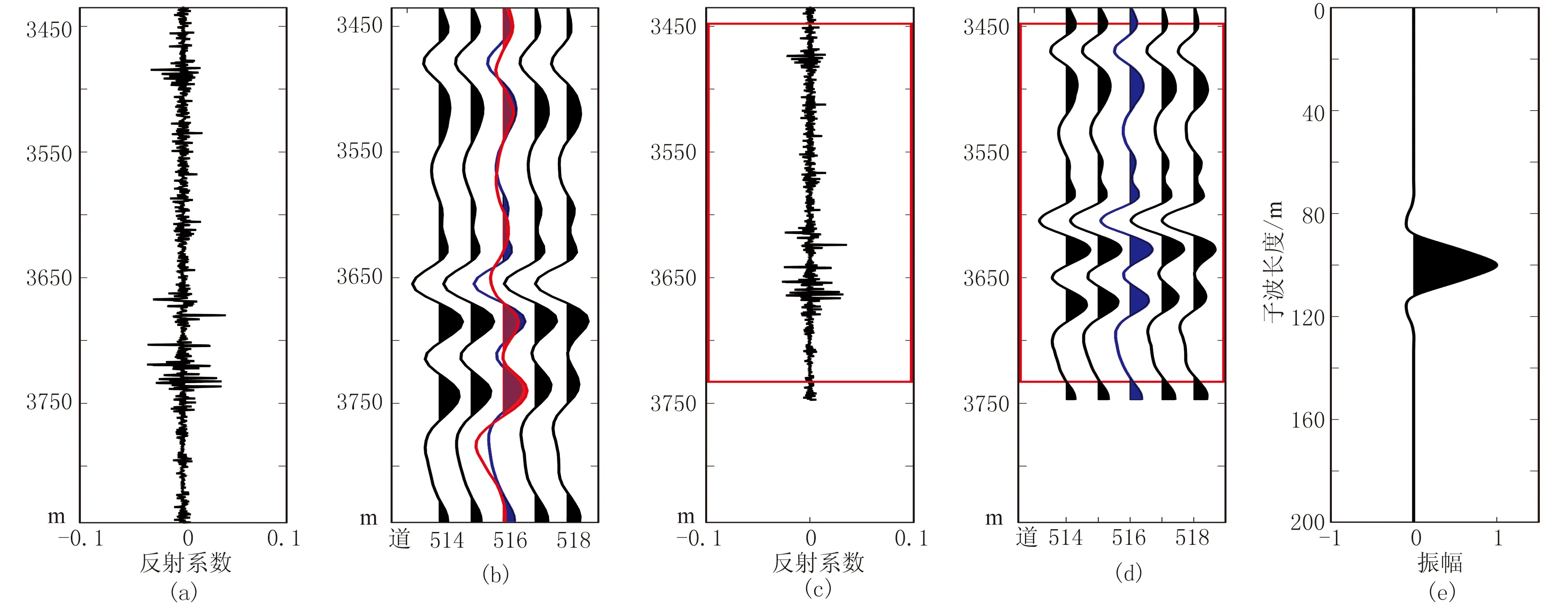
圖8 B井測井數據及地震子波提取結果
4 結束語
本文提出了基于子空間約束Huber范數的深度域地震子波提取方法,該方法不涉及正則化參數,且容易給定初始地震子波和閾值。雖然該方法使用了迭代求解方案,但相較于其在精度和可靠性上的顯著提升,計算量的少許增加是能夠接受的。更為重要的是,與一些常規方法相比,本文方法從較短的深度域數據中提取的地震子波更可靠,這對于反映深度域地震子波隨深度變化的特征,并根據需要提取深變地震子波具有重要意義。

