懸掛式單軌交通系統連續軌道梁橋靜力分析與截面參數比較研究

邱靖權,鄭凱鋒,熊籽躒

(西南交通大學土木工程學院,成都 610031)

引言

隨著我國經濟的迅猛發展以及城市化水平的不斷提高，城市擁堵以及汽車排放污染等問題逐漸凸顯，而城市軌道交通的出現，有效地緩解了這些問題。懸掛式單軌交通系統作為新型城市軌道交通，起步雖然晚于地鐵和跨座式軌道交通，但憑借其地形適應能力強，能耗低、運輸量適中和環境友好型[1-3]等一系列優點，在中等城市中具有廣闊的發展前景[4-6]。目前，我國多座城市已開始規劃和布局相應交通線路。

與傳統的軌道梁不同，懸掛式單軌系統橋梁的軌道梁是實現其跨越能力的關鍵構件，軌道梁截面形式為下部開口箱梁，呈Π形。編組列車的走行輪及轉向輪均在梁內，走行輪行走于底板上，列車的轉向依靠腹板及與其接觸的轉向輪實現，因此軌道梁的設計、制造以及安裝的精度均有非常嚴格的要求[7]；同時線路的電纜、管道等也均放置于軌道梁內，降低了相應養護維修成本[8-9]。

目前，德國與日本的懸掛式單軌系統技術已經相當成熟，并且已經應用于多條軌道線路[10-14]。而國內引進懸掛式軌道交通系統時間較短，缺乏系統性研究以及設計經驗，并且尚未統一設計標準，故目前已有的設計方案均相對保守[15-18]。為保證懸掛式單軌交通系統設計的經濟性與合理性，并為我國相關設計人員提供參考，結合一座懸掛式連續鋼軌道梁橋設計，分析計算其在各個荷載組合下的應力與變形，研究各截面參數對結構強度、剛度以及用鋼量的影響，最后以用鋼量最少為目標進行適當參數削減，提出新方案，并建立新方案下的有限元模型進行強度和剛度檢算。

1 方案設計

本文分析采用的懸掛式單軌交通系統連續軌道梁橋為(40+60+40) m鋼結構軌道梁，兩線軌道梁之間采用鋼橫梁連接，全橋鋼梁采用Q345qD，總體布置如圖1所示。

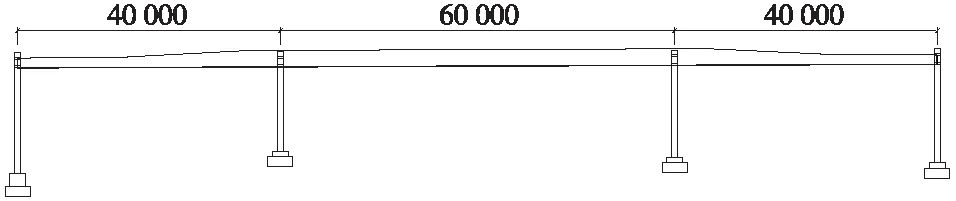
圖1 總體布置(單位：mm)

懸掛式軌道梁橋的橋墩形式主要分為單線的倒L形和雙線的門形、T形以及球拍形橋墩[19]。本橋的橋墩為門形墩，如圖2所示，與傳統門形墩不同，懸掛式單軌系統軌道梁并不是放置在門形墩的蓋梁頂部，而是從蓋梁下伸出兩塊吊梁，吊梁水平伸出牛角以放置支座并承受軌道梁傳遞的荷載。

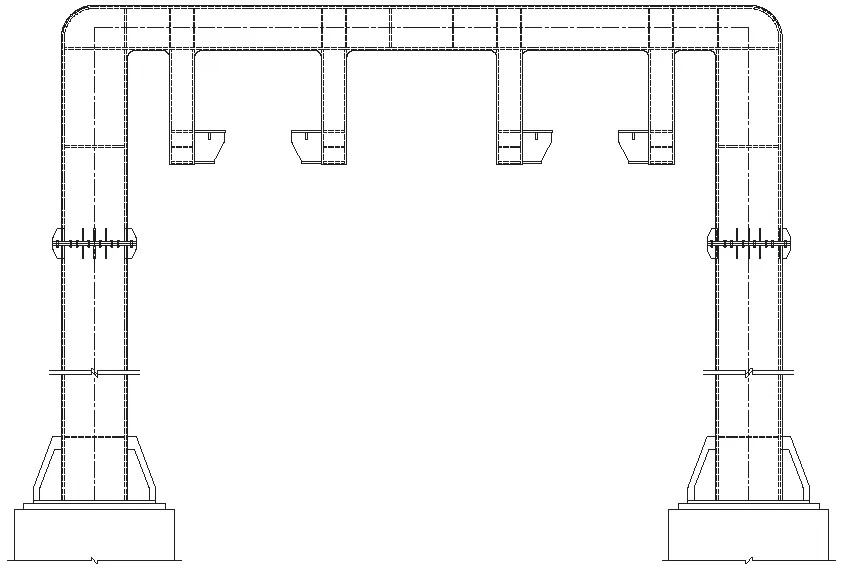
圖2 門形墩構造形式

軌道梁采用Π形截面，且為變截面，截面在中跨梁高最大且為2.5 m，在邊跨靠近支座處梁高最小且為1.5 m，軌道梁截面形式如圖3所示。此外，支座處的軌道梁頂板寬為1.372 m，在其余處頂板寬為1.172 m；頂板厚度為36 mm，頂板加勁肋厚度為30 mm，沿縱向每1 m布置1道頂板加勁肋，在支座處加密。腹板厚度為36 mm，腹板加勁肋厚度為30 mm，沿縱向每1 m布置1道腹板加勁肋，并在支座處加密。局部加勁底板的最薄處厚度為32 mm，底板加勁肋厚度為30 mm，沿縱向每1 m布置1道底板加勁肋，并在支座處進行加密。兩線軌道梁之間除支座處不布置橫梁外，其余位置每隔5 m設置1道橫梁。

圖3 軌道梁截面形式(單位：mm)

2 連續軌道梁橋靜力分析

2.1 有限元模型

運用MIDAS/CIVIL建立全橋梁單元模型，雙線鋼軌道梁分開建模。軌道梁的每段梁單元長度為1 m并在支座處加密，每片橫梁分為3段；橋梁的支座為球形鋼支座，采用彈性連接模擬鋼軌道梁與橋墩之間的連接，并且由于橫向支座中心間距小于4 m，故將每個支座都進行橫向約束；橋墩蓋梁在橫橋向均勻分段，并在吊板處適當加密；墩底采用固結約束。全橋模型共有659個節點，609個單元，全橋空間梁單元模型整體結構如圖4所示。

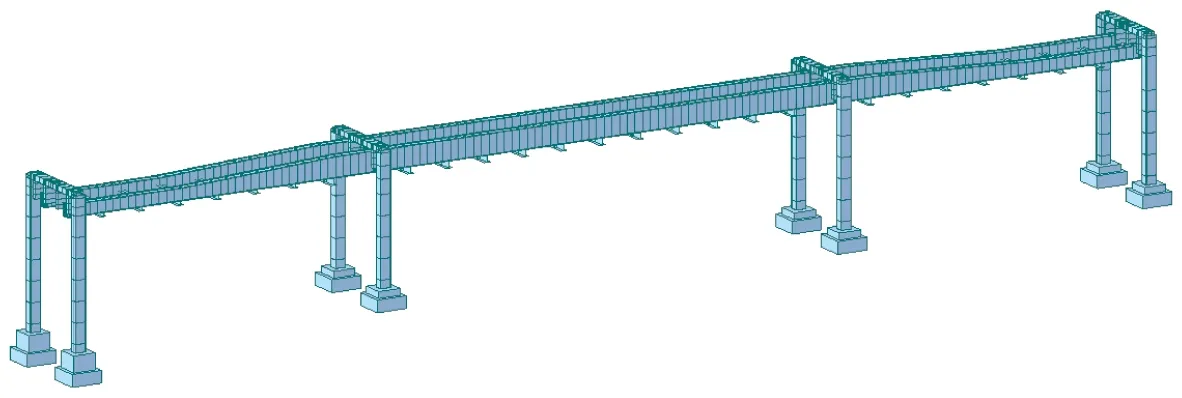
圖4 全橋梁單元模型

2.2 荷載類型及其組合

由于國內暫無懸掛式單軌系統的統一規范，本文依照專門編寫的《四川省懸掛式單軌設計規范》中條文提出的要求在靜力計算中考慮以下荷載：(1)結構自重與附屬設備及附屬建筑自重；(2)列車豎向靜活載；(3)列車豎向動力作用；(4)列車橫向搖擺力；(5)列車制動力；(6)風力；(7)溫度影響力。

根據規范要求，列車豎向靜活載采用最大軸重為4.5 t的兩輛編組列車，每輛編組列車各有6對車軸，4個重軸軸重4.5 t，中間兩個輕軸軸重0.75 t；兩輛編組列車之間的軸距為2.1 m，相鄰重軸間距為1.6 m，相鄰輕軸間距為3.6 m，重軸與輕軸間距為0.95 m，列車各軸重布置如圖5所示。

圖5 列車靜活載軸重布置(單位：m)

根據不同荷載組合，將材料基本容許應力和地基容許承載力乘以不同的提高系數，提高系數按表1選取，以此計算分析橋梁運營階段下各最不利工況的內力、應力及變形。

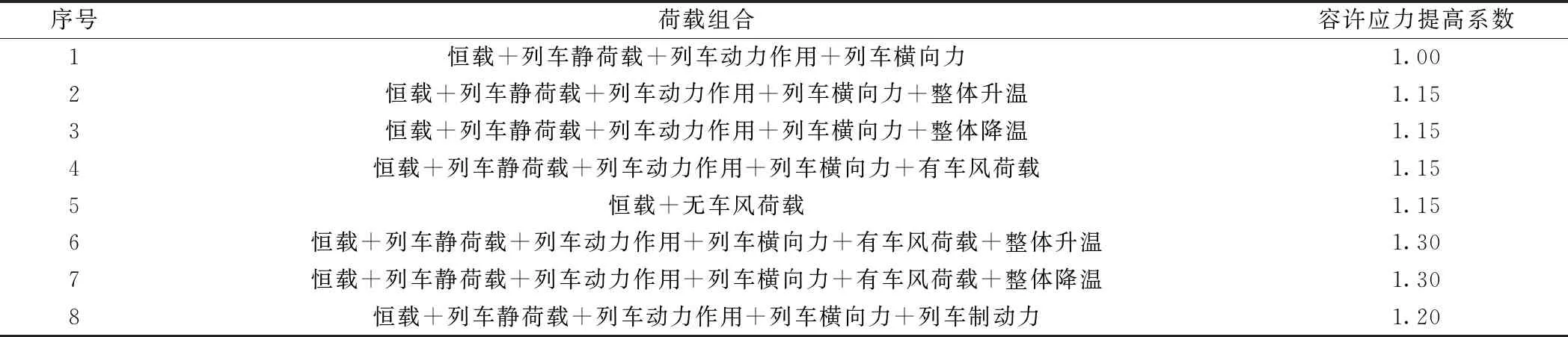
表1 荷載組合及容許應力提高系數

2.3 計算分析

計算得到軌道梁主梁在列車豎向靜活載作用+0.5倍溫度影響力下產生的最大撓度值為23.72 mm，小于《四川省懸掛式單軌設計規范》規定的限值66.00 mm，如圖6所示；而列車靜活載作用下軌道梁橋由于撓度產生的梁端轉角為1.73‰，小于規范規定的3.00‰，如圖7所示。各個荷載組合作用下的應力計算匯總如表2所示。

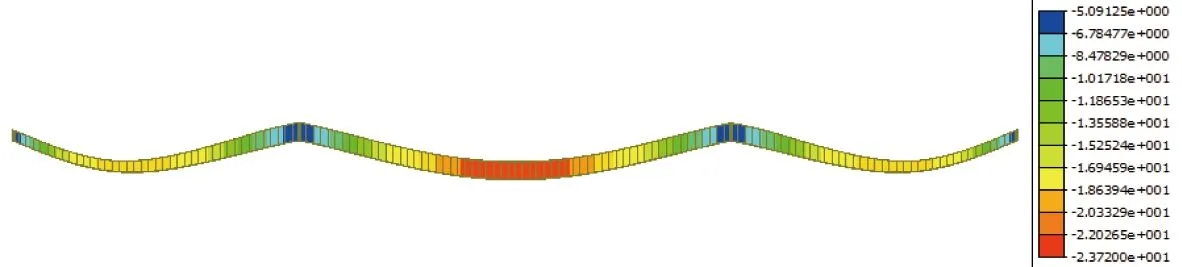
圖6 列車豎向靜活載+0.5倍溫度作用下的撓度(單位：mm)

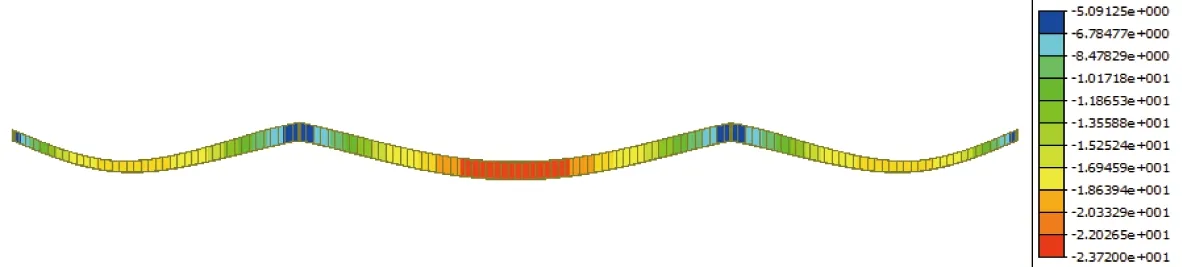
圖7 列車靜活載作用下的梁端轉角(單位：rad)

計算結果表明，在組合3(恒載+列車活載+列車橫向搖擺力+整體降溫)作用下，鋼主梁上緣產生最大組合應力80.0 MPa，并在下緣產生最小組合應力-81.0 MPa；而在組合6(恒載+列車活載+列車橫向搖擺力+有車風荷載+整體升溫)作用下，鋼主梁上緣產生最小組合應力-55.0 MPa，并在下緣產生最大應力58.6 MPa；并且在組合7作用下，橫梁產生最大組合應力和最小組合應力，其中最大組合應力為37.0 MPa，最小組合應力為-28.7 MPa。軌道梁各個部件在各個荷載組合下的組合應力極值均遠小于相關設計規范條文所規定限值要求。

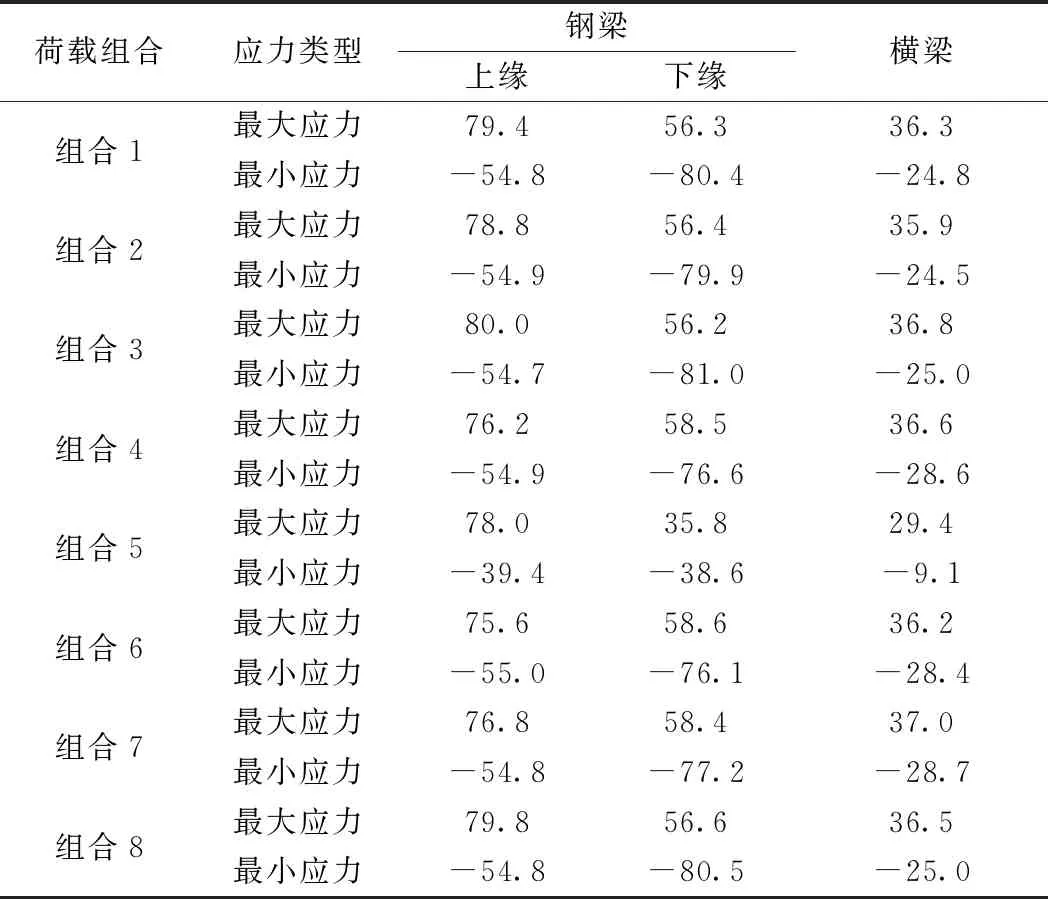
表2 軌道梁應力計算匯總 MPa

3 軌道梁截面參數比較分析

根據計算分析，本橋在各個荷載組合下的頂板、底板和腹板的最大應力以及變形等均遠小于規范限值，鋼材性能并未得到充分利用，不僅增加了工廠制造成本，也增加了現場施工的難度[20]。基于以上原因，利用MIDAS/CIVIL軟件分別對軌道梁變截面高度、頂板厚度、腹板厚度和底板厚度等進行參數影響分析。根據參數分析結果進行適當的參數削減，以達到減少用鋼量，降低成本，使設計更為合理的目的。

由各荷載組合下結構應力計算結果可知，各荷載組合下的軌道梁最大和最小組合應力差異并不大。取最不利的荷載組合3(恒載+列車靜荷載+列車動力作用+列車橫向力+整體降溫)對不同參數條件下的結構應力和變形進行對比分析，各截面參數如圖8所示。

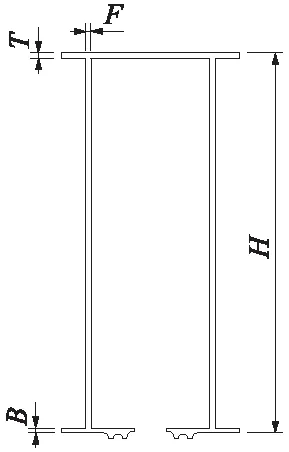
圖8 截面參數

3.1 變截面高度影響分析

梁高是影響橋梁剛度的重要因素之一，軌道梁的高度越高，則其剛度越大，但與此同時其自身的重力也會相應增加，因此梁高越高并不一定越有利于受力和變形。本橋邊跨支點處截面高1.5 m，中跨支點處截面高為2.5 m，在滿足軌道梁剛度和強度以及其他參數不變的條件下，分別取中支點處截面高度H為2.3，2.1，1.9，1.7 m和1.5 m，采用中跨等截面邊跨變截面設計，其中H=1.5 m時為等截面設計。

對以上幾組參數分別建立有限元模型進行分析，并與原方案結果(最大梁高為2.5 m)進行對比，計算得到各最大梁高下的軌道梁應力、豎向撓度以及梁端轉角如表3所示。

表3 不同最大梁高下的軌道梁應力與變形

3.2 頂板厚度影響分析

頂板厚度對于結構的強度與剛度也有一定的影響，在滿足軌道梁剛度和強度以及其他參數不變的條件下，逐漸減小頂板厚度以分析其對結構受力與變形的影響。分別取頂板厚度T為32，28，24，20 mm和16 mm分別建立有限元模型進行分析，并與原結果(頂板厚度為36 mm)進行對比。計算得到各頂板厚度下的軌道梁應力、豎向撓度以及梁端轉角如表4所示。

表4 不同頂板厚度下的軌道梁應力與變形

3.3 腹板厚度影響分析

在滿足軌道梁剛度和強度以及其他參數不變的條件下，逐漸減小腹板厚度以分析其對結構受力與變形的影響。分別取腹板厚度F為32，28，24，20 mm和16 mm分別建立有限元模型進行分析，并與原結果(腹板厚度為36 mm)進行對比。計算得到各腹板厚度下的軌道梁應力、豎向撓度以及梁端轉角如表5所示。

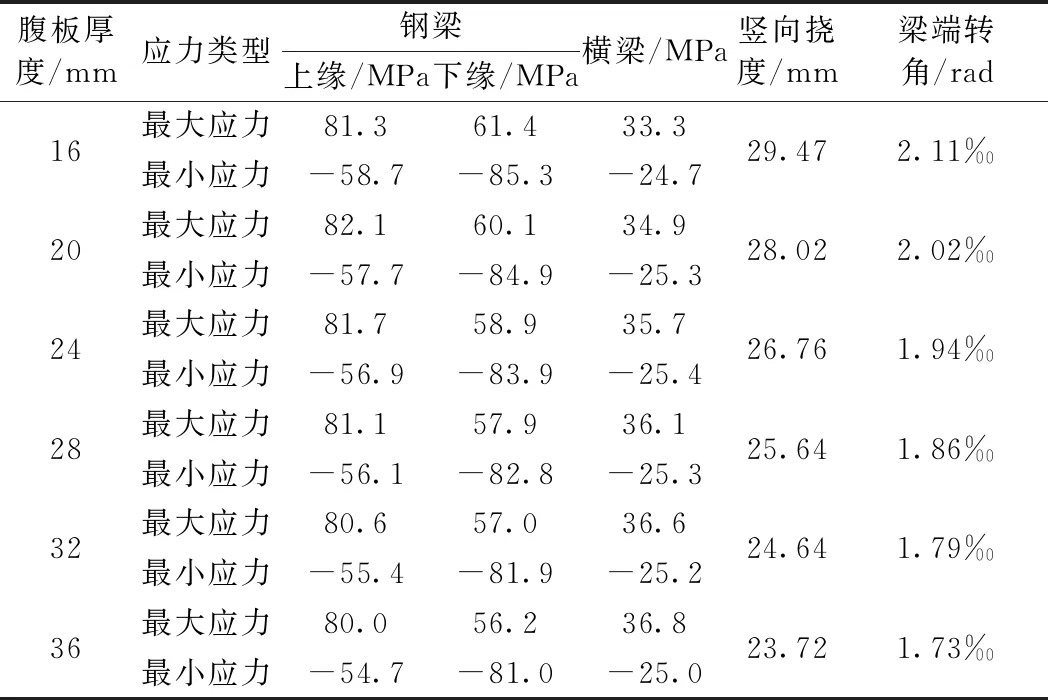
表5 不同腹板厚度下的軌道梁應力與變形

3.4 底板厚度影響分析

在滿足軌道梁剛度和強度以及其他參數不變的條件下，逐漸減小底板厚度B以分析其對結構受力與變形的影響。由于底板內側最薄處只有20 mm，故只能分別取底板外側最厚處厚度B為28，24 mm和20 mm分別建立有限元模型進行分析，并與原結果(底板最厚處厚度為32 mm)進行對比。計算得到各底板厚度下的軌道梁應力、豎向撓度以及梁端轉角如表6所示。

3.5 軌道梁截面參數比較分析

梁高為1.5 m的軌道梁總長30 m，變截面軌道梁總長40 m，最大梁高H的軌道梁總長70 m，因此可得到頂板、腹板、底板所用鋼材體積V1(m3)、V2(m3)和V3(m3)分別為

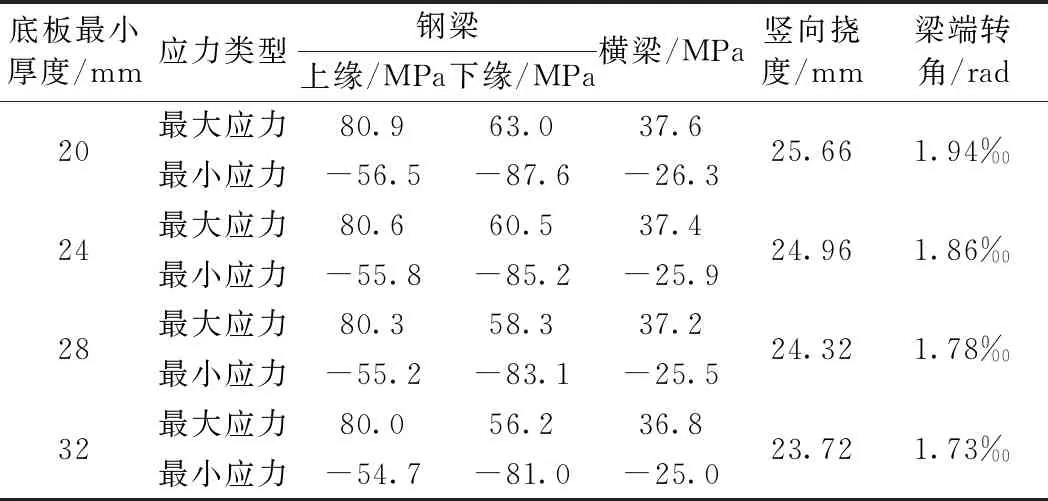
表6 不同底板厚度下的軌道梁應力與變形

V1=

(1)

V2=

0.09HF+0.075F

(2)

(3)

軌道梁的總用鋼體積V=V1+V2+V3，當頂板厚T在16～40 mm，腹板厚F在16～36 mm，底板厚B在20～32 mm，最大梁高H在1.5～2.5 m范圍內時，將式(1)到式(3)相加得到總用鋼體積V(m3)后，分別對T、H、F、B求偏微分，可以得到各偏微分值的范圍如表7所示。

表7 總用鋼體積V對各截面參數偏微分值范圍

由表7可以得到，對于總用鋼體積(總用鋼量)而言，各參數影響程度從大到小依次是最大梁高H，腹板厚度F，頂板厚度T，底板厚度B。

綜合軌道梁變截面高度、頂板厚度、腹板厚度和底板厚度對其豎向撓度、梁端轉角與應力的影響，可以看出：(1) 對于豎向撓度，影響程度從大到小依次是最大梁高H，腹板厚度F，頂板厚度T，底板厚度B；(2) 對于梁端轉角，影響程度從大到小依次是最大梁高H，頂板厚度T，底板厚度B，腹板厚度F；(3) 對于鋼梁最大應力，影響程度從大到小依次是最大梁高H，頂板厚度T，腹板厚度F，底板厚度B；(4) 對于鋼梁最小應力，影響程度從大到小依次是最大梁高H，底板厚度B，腹板厚度F，頂板厚度T。因此，各項軌道梁截面參數對鋼梁應力、變形以及用鋼量的影響如表8所示。

表8 各截面參數對軌道梁應力、變形及用鋼量影響程度

由于各條件下的鋼梁應力均遠小于規范規定的容許應力，因此以豎向撓度和梁端轉角滿足規范要求為條件，以用鋼量最小為目標，提出截面材料最省方案，最后再建模對強度進行檢驗。

根據得出的各截面參數與豎向撓度和梁端轉角的關系，可以推出保持最大梁高H為最小值1.5 m，腹板厚度F與底板厚度B保持最初設計值不變，適當增加頂板厚度T，可在滿足剛度要求的情況下，達到用鋼量最小的目的。最終得到在用鋼量最省的情況下的各截面參數值分別為：最大梁高H為1.5 m，腹板厚度F為36 mm，底板最厚處厚度B為32 mm，頂板厚度T為40 mm。建立梁單元模型，進行分析計算之后得到鋼梁應力、變形以及與原設計結果的對比如表9所示。

表9 新舊方案軌道梁應力與變形對比

根據表9可知，在保證軌道梁剛度的情況下，以減小用鋼量為目標得到的新方案下軌道梁強度依然滿足要求，并且用鋼量減少16.4%，約39.827 t；同時，變截面連續軌道梁變為了等截面連續軌道梁，也減少了工廠加工成本以及現場施工難度。

4 結論

結合(40+60+40) m懸掛式連續鋼軌道梁橋設計，通過MIDAS/CIVIL軟件建立全橋梁單元模型，計算各荷載組合下結構的應力與變形，并分析各截面參數對結構應力、變形以及用鋼量的影響，最后以用鋼量最省為目標提出新方案，并進行強度、剛度驗算，得到結論如下。

(1) 原設計方案在最不利荷載組合作用下的變形與應力均滿足規范要求，且變形與應力幅值均遠未達到規范容許限值。

(2) 提出的新方案結構強度與剛度均滿足規范要求，并且用鋼量較原設計方案減少了16.4%，約38.827 t；同時變截面連續梁變為等截面連續梁，降低了工程成本及現場施工難度。