基于SVD分解的二階離散時變線性系統穩定性分析

付 波 張行星 范秀香 趙熙臨 何 莉

(湖北工業大學太陽能高效利用及儲能運行控制湖北省重點實驗室 湖北 武漢 430068)

0 引 言

離散線性時不變系統的漸進穩定性可以通過判定系統狀態矩陣的特征值是否位于復平面單位圓內來判斷[1]，但是時不變系統的穩定性判據并不適用于離散時變線性系統。凍結法利用線性時不變系統的穩定性判據判斷特定條件下線性時變系統的穩定性，但其理論不夠嚴密。

控制系統可以分為離散線性系統和連續線性系統，連續系統的研究相對于離散系統更為完善,但離散系統也起重要作用，很多離散系統可通過連續系統離散化得到，目前已有Euler、Runge-Kutta等離散化方法[2-3]。但連續系統離散化得到的離散系統是否具有原連續系統的穩定性相關性質，依舊是需要繼續研究的問題。控制系統穩定性判斷[4]方法通常分為兩類，一類主要研究系統方程需要滿足的條件，另一類是尋求李雅普諾夫函數。對于離散線性系統的研究[5]，主要集中在差分方程和微分方程的改造。

齊春子等[6]研究了多變量全系數黃金分割反饋控制系統的穩定性問題，得到了此類閉環系統時變參數變化速度的約束條件。張振國等[7]通過構造L函數，分析了二階離散時變線性系穩定性的充分條件。關軼峰等[8-9]基于李雅普諾夫理論，提出了離散時變線性系統的充分條件。

本文在這些研究的基礎上，對線性離散時變系統的經典狀態矩陣做SVD分解，從而得到新的等效狀態方程，從李雅普諾夫定理的思路進行思考，經過推導和驗證，得到了兩個判定線性離散時變系統的穩定性判據和兩個不穩定判據。

1 二階離散時變線性系統及其穩定性

1.1 正交多項式三相遞歸式穩定性分析

若f(x)，g(x)∈C[a,b]，ρ(x)為[a,b]上的權函數，且：

(1)

則稱f(x)與g(x)在[a,b]上帶權ρ(x)正交。只要給定[a,b]上的權函數ρ(x)，由{1,x,…，xn，…}利用逐個正交化手續得到正價多項式序列:

(2)

并且滿足遞推關系:

ρn+1(x)=(x-αn)ρn(x)-βnρn-1(x)n=0,1,…

(3)

其中：

ρ0(x)=1ρ-1(x)=0

(4)

式中：(x-αn)和βn為遞歸式的系數。

把式(3)的階數n作為一個離散變量進行思考，則式(3)便可以看成一個離散時變線性系統進行分析。

1.2 李雅普諾夫穩定性定理

定義1說明，對于每一個球域S(ε)，若存在一個球域S(δ)，當t→∞時，從S(δ)球域出發的軌跡不離開S(ε)球域，則系統的平衡狀態在李雅普諾夫意義下是穩定的，如圖1(a)所示。

(a)穩定

漸進穩定性是個局部穩定的概念，圖1(b)中的球域S(δ)是漸進穩定的范圍。

定義3如果從S(δ)球域出發的軌跡，無論S(δ)球域選得多么小，至少有一條軌跡脫離S(ε)球域，則稱平衡狀態xe為不穩定的。如圖1(c)中的軌跡曲線(2)所示。

1.3 SVD穩定性分析

定義二階離散線性時變系統：

X(k)=G(k)X(k-1)

(5)

式中：2×2狀態矩陣G(k)∈C2×2，rankG(k)=2(2>0)。一般采用李雅普諾夫第二法分析系統的穩定性，但是李雅普諾夫函數不易構造。即使構造出該函數，在判定能量增量正定性(或負定性)的過程中，也可能因不等式運算而大大縮小系統穩定或不穩定區間。

對狀態矩陣G(k)作SVD分解，存在二階酉矩陣U(k)和V(k)，使得：

G(k)=U(k)S(k)V(k)T

(6)

式中：S(k)=diag(σ1(k),σ2(k))由G(k)唯一確定，σ1(k)≥σ2(k)>0，σi(k)(i=1,2)為G(k)正奇異值；U(k)、V(k)是非唯一酉矩陣。把U(k)、V(k)作為單位旋轉矩陣進行討論，式(5)表示為：

X(k)=U(k)S(k)V(k)TX(k-1)

(7)

將式(7)展開得:

X(k)=U(k)S(k)V(k)T…U(1)S(1)V(1)TX(0)

(8)

重定義R(k)=U(k)，R(k-1)=V(k)TU(k-1)，Y(0)=V(1)TX(0)，Y(k)=X(k)，得：

Y(k)=R(k)S(k)R(k-1)S(k-1)…R(1)S(1)Y(0)

(9)

易得單位旋轉矩陣R(k)：

(10)

令D(k)=R(k)S(k),對于D(k)序列，雖然第k項D(k)的表達式與其他序列不同，但它不影響式(7)的狀態穩定性,那么有以下RS系統：

Y(k)=D(k)Y(k-1)

(11)

可見，對二維離散時變線性系統的分析可以等價于對式(11)進行分析，式(5)的穩定性分析也可以等價于對式(11)進行分析。

式(5)中每一個狀態矩陣G(k)可以轉化成式(9)的兩個矩陣R(k)與S(k)，圖2為矩陣R(k)與矩陣S(k)的作用效果。R(k)可以使向量i逆時針單位旋轉θ(k)，但并不會改變i的幅值。考慮到σ1(k)>σ2(k)，則矩陣S(k)會讓向量i在一、三象限進行角度為ω′(k)的順時針方向旋轉(在二、四象限進行同樣角度的逆時針旋轉)，并且改變向量模值的大小。

(a)旋轉效果R(k)

2 RS系統穩定性分析

2.1 單象限運動穩定性分析

定理1如圖3所示，討論一類RS系統，Y(k)=D(k)Y(k-1),k=2,3,…,在二維相平面y1-y2內，其狀態軌跡最終保持在第一或第三象限。

圖3 穩定性運動軌跡的模型

已知σ1(k)>σ2(k)，σ2(k)<1，當滿足:

0<θ(k)≤θmax(k)

(12)

0<κ2(k)<κ′(k)

(13)

和

(14)

式(11)穩定。

式中：

2.2 單象限運動不穩定性分析

定理2如圖4所示，討論一類RS系統，Y(k)=D(k)Y(k-1),k=2,3,…,在二維相平面y1-y2內，其狀態軌跡最終保持在第一或第三象限。

圖4 RS系統單象限不穩定情況

已知σ1(k)>σ2(k)，σ2(k)<1，當滿足：

0<θ(k)≤θmax(k)

(15)

0<κ2(k)<κ′(k)

(16)

和

(17)

式(11)不穩定。

式中：

2.3 二四對象限對向運動穩定性分析

如圖5所示，討論一個RS系統，其狀態軌跡保持在第二與第四象限對向運動。

圖5 RS系統兩象限穩定情況

定理3對于式(11)，在二維相平面y1-y2內，已知σ1(k)>σ2(k)，σ2(k)<1，當滿足：

θmin(k)≤θ(k)<π

(18)

0>κ2(k)>κ′(k)

(19)

和

(20)

式(11)穩定。

式中：

2.4 一三對象限對向運動不穩定性分析

如圖6所示，討論一個RS系統，其狀態軌跡保持在第一與第三象限對向運動。

圖6 RS系統兩象限不穩定情況

定理4對于式(11)，在二維相平面y1-y2內，已知σ1(k)>σ2(k)，σ2(k)<1，當滿足：

(21)

0<κ′(k)<κ*(k)

(22)

和

(23)

式(11)不穩定。

3 實驗分析

3.1 單象限運動穩定性實驗

Krawtchouk多項式構成的離散時變系統迭代公式如下：

(24)

式中：x=100，p=0.6，N=400。pk(x)初值為(1,1)。

圖7為旋轉角度θ(k)與極限角度θmax(k)、G(k)的奇異值σ1(k)和σ2(k)、RS變換前后相量模值比H(k)、臨界斜率κ2(k)和κ′(k)。圖7(c)和(e)顯示，當k>1，有0<θ(k)<θmax(k),且0<θ(k)<π/2, 0<κ2(k)<κ′(k)，滿足式(12)和式(13)；圖7(d)顯示σ1(k)>σ2(k)>0；圖7(a)中，當k>5時，有H(k)<1，符合式(14)。由定理1可知，Krawtchouk多項式的三項遞歸計算在點x=100處穩定。

(a)模值比函數H(k)

Krawtchouk多項式在點x=100遞歸計算的絕對誤差和相對誤差分別記錄在圖8(a)和圖8(b)。由圖8(a)可知，當045時，絕對誤差開始減小并趨于穩定；由圖8(b)可得相對誤差在極小的區間先增大然后減小并趨于穩定，絕對誤差與相對誤差的趨勢都符合定理1。所以Krawtchouk多項式在x=100具有遞歸數值穩定的性質，而以Krawtchouk多項式作為核函數的Krawtchouk矩也具有相同的穩定性性質。

(a)絕對誤差

3.2 單象限運動不穩定性實驗

某離散時變系統多項式迭代公式如下：

(25)

式中：x=390，N=400，p=0.9。

圖9為旋轉角度θ(k)與極限角度θmax(k)、G(k)的奇異值σ1(k)和σ2(k)、RS變換前后相量模值比H(k)、臨界斜率κ2(k)和κ′(k)。圖9(c)和(e)顯示，當k>1，有0<θ(k)<θmax(k),且0<θ(k)<π/2,0<κ2(k)σ2(k)>0；圖9(a)中，當k>28時，有H(k)>1，符合式(17)。由定理2可知，該離散系統多項式的三項遞歸計算在點x=390處穩定。

(a)模值比函數H(k)

該離散系統的多項式在點x=390遞歸計算的絕對誤差和相對誤差分別記錄在圖10(a)和圖10(b)。由圖10(a)可知，當k>0時，絕對誤差和相對誤差均一直增大，相對誤差增長趨勢較絕對誤差增長趨勢稍緩，但都發散，與定理2的結論一致。因此該離散系統的多項式至少存在一點x=390具有遞歸數值不穩定。

(a)絕對誤差

3.3 二四對象限穩定性實驗

Krawtchouk多項式構成的離散時變系統迭代公式如下：

(26)

式中：x=390,p=0.6,N=400。pk(x)的初值為(1,-1)。

圖11記錄了旋轉角度θ(k)與極限角度θmin(k)、G(k)的奇異值σ1(k)和σ2(k)、RS變換前后相量模值比H(k)、臨界斜率κ2(k)和κ′(k)。圖7(c)和(e)顯示，當k>1，有0<θ(k)<θmax(k)且π/2<θ(k)<π, 0<κ′(k)<κ2(k)，滿足式(18)和式(19)；圖11(d)顯示σ1(k)>σ2(k)>0；圖11(a)中，當k>6時，有H(k)<1，符合式(20)。由定理3可知，Krawtchouk多項式的三項遞歸計算在點x=390處穩定。

(a)模值比函數H(k)

Krawtchouk多項式在點x=390遞歸計算的絕對誤差和相對誤差分別記錄在圖12(a)和圖12(b)中。由圖12(a)可見當0190時絕對誤差和相對誤差都減小并趨于穩定。絕對誤差與相對誤差都符合定理3。因此Krawtchouk多項式至少存在一點，該點在x=390時，多項式具有數值穩定性的性質，以x=390具有遞歸數值穩定，使Krawtchouk多項式作為核函數的矩也具有相同的穩定性。

(a)絕對誤差

3.4 一三對象限不穩定性實驗

某離散時變系統多項式迭代公式如下：

(27)

式中：x=390，p=0.9，N=400。pk(x)初值為(1，1)。

圖13為旋轉角度θ(k)與極限角度θmin(k)、G(k)的奇異值σ1(k)和σ2(k)、RS變換前后相量模值比H(k)、臨界斜率κ*(k)和κ′(k)。圖13(c)和(e)顯示，當k>50，有0<θmin(k)<θ(k)且π<θ(k)<3π/2,0<κ*(k)<κ′(k)，滿足式(21)和式(22)；圖13(d)顯示σ1(k)>σ2(k)>0；圖13(a)中，當k>25時，有H(k)>1，符合式(23)。由定理4可知，該離散系統多項式的三項遞歸計算在點x=390處不穩定。

(a)模值比函數H(k)

該離散系統多項式在點x=390遞歸計算的絕對誤差和相對誤差分別記錄在圖14(a)和圖14(b)中。由圖14(a)可得當098時絕對誤差又開始增大并趨于發散；由圖14(b)可得當0150時相對誤差又開始增大并趨于發散。由此可得絕對誤差與相對誤差都與定理4的結論一致，該離散系統多項式至少存在一點x=390具有遞歸數值不穩定。

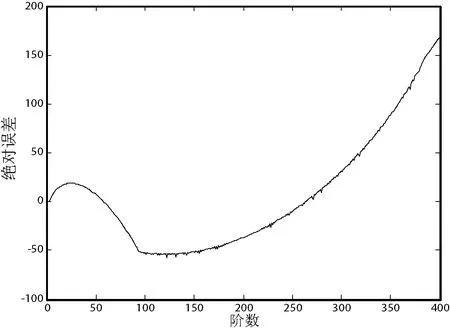
(a)絕對誤差

4 結 語

本文通過SVD分解建立新的離散線性時變系統RS模型，基于李雅普諾夫定理提出關于二階離散時變線性系統的兩個穩定性判斷充分條件和兩個不穩定性判斷充分條件。實驗結果驗證了所提出的離散線性時變系統穩定性與不穩定性判斷條件的有效性。