對2020年全國卷Ⅰ理科第20題的多視角探究

◇ 江西 李樹森 孫 強

直線與圓錐曲線的綜合問題是高考的重點、熱點問題,此類問題往往運算量大.解決此類問題常常需要將題干中的幾何條件轉化為坐標形式,其關系式中需要含有x1＋x2和x1x2,并運用根與系數的關系求解,但是有一類問題其坐標形式中不會出現x1＋x2和x1x2,解決此類問題就需要抓住x1與x2或y1與y2的系數不相等(非對稱),借助曲線方程、代數變形、和與積關系的轉換等手段,調整為對稱.本文以2020年全國卷Ⅰ理科第20題為例,從五種不同的視角探究這一類問題的解題策略.

1 試題呈現

題目(2020年全國卷Ⅰ理科第20題)已知A,B分別為橢圓的左、右頂點,G為E的上頂點為直線x＝6上的動點,PA與E的另一交點為C,PB與E的另一交點為D.

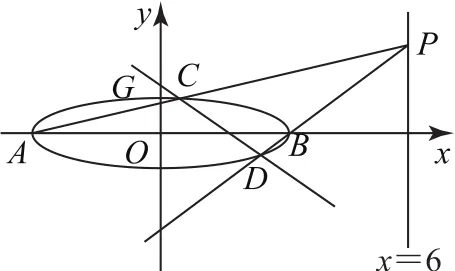
圖1

(1)求E的方程;

(2)證明:直線CD過定點.

2 命題背景

1)極點、極線定義:已知圓錐曲線Γ:Ax2＋By2＋Cx＋Dy＋F＝0,則稱點P(x0,y0)和直線l:別是圓錐曲線Γ的一對極點和極線.

2)定理(配極原則):點P關于圓錐曲線Γ的極線p經過點Q?點Q關于圓錐曲線Γ的極線q經過點P?直線q關于圓錐曲線Γ的極點Q在直線p上.由此定理可知,共線點的極線必共點,共點線的極點必共線.

3 試題分析

本題是一道典型的直線與圓錐曲線綜合問題,涉及的直線多、點多,是一道關系錯綜復雜的動態問題.同時在本題中出現了一對關于原點的對稱點,具有很多重要的性質.涉及多線與多點的問題,常常需要我們選擇主動線、主動點來處理,如何巧設變量、建立關系更值得我們深思.問題中直線CD與兩個不同點關聯,因此利用幾何關系得出來的x1與x2或y1與y2的關系,一般會出現不對稱,直接利用根與系數的關系處理比較困難,如何突破化簡運算更是一個重要的環節.下面從設點和設線兩種方向處理,圍繞著如何突破運算,深入探究本題第(2)問的解法.

4 解法探究

視角1選擇P為主動點,設單參數并表示直線CD的直線方程.

解法1因為A(－3,0),B(3,0),設P(6,d),則直線PA,PB的方程分別為

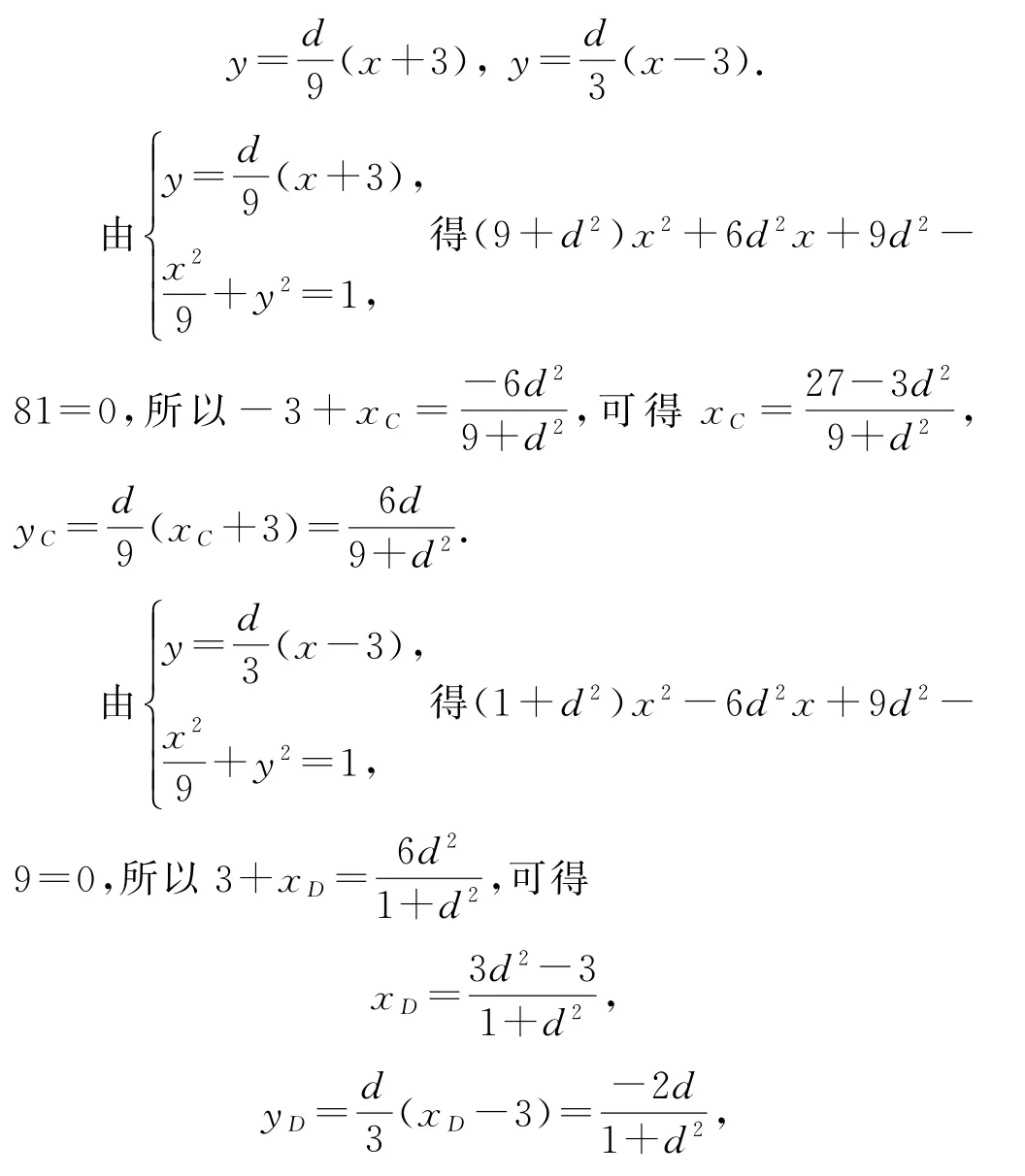
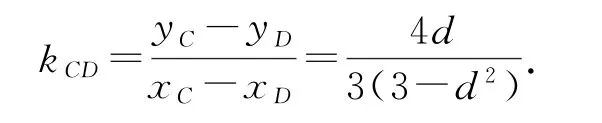
直線CD的方程為

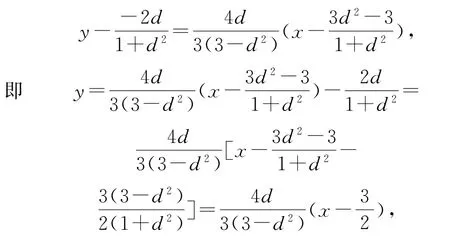
故得直線CD過定點.

點評

此方法處理過程中視動點P為主動點,設點P(6,d),并通過聯立直線PA,PB與橢圓方程,利用根與系數的關系直接求解出C,D的坐標,并求出直線CD的方程,對直線方程適當變形得到直線CD過定點這種方法很常見,但是運算量大,對代數的變形能力要求高.

視角2通過直線CD的特殊位置猜想其定點,并設點轉化為共線向量證明其結論成立.

解法2由對稱性可知,直線CD必經過x軸的定點,且CD⊥x軸.

設C(x0,y0),D(x0,－y0),得A(－3,0),B(3,0),設P(6,d),則即kPB＝3kPA.

因為C,H,D三點共線,則設C(x1,y1),D(x2,y2),則

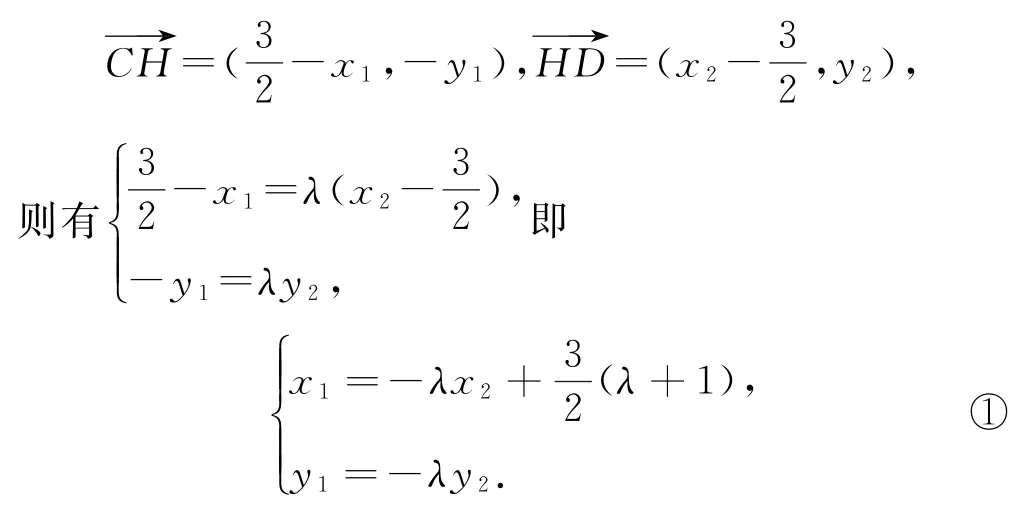
因為C(x1,y1),D(x2,y2)為橢圓上的點,則有

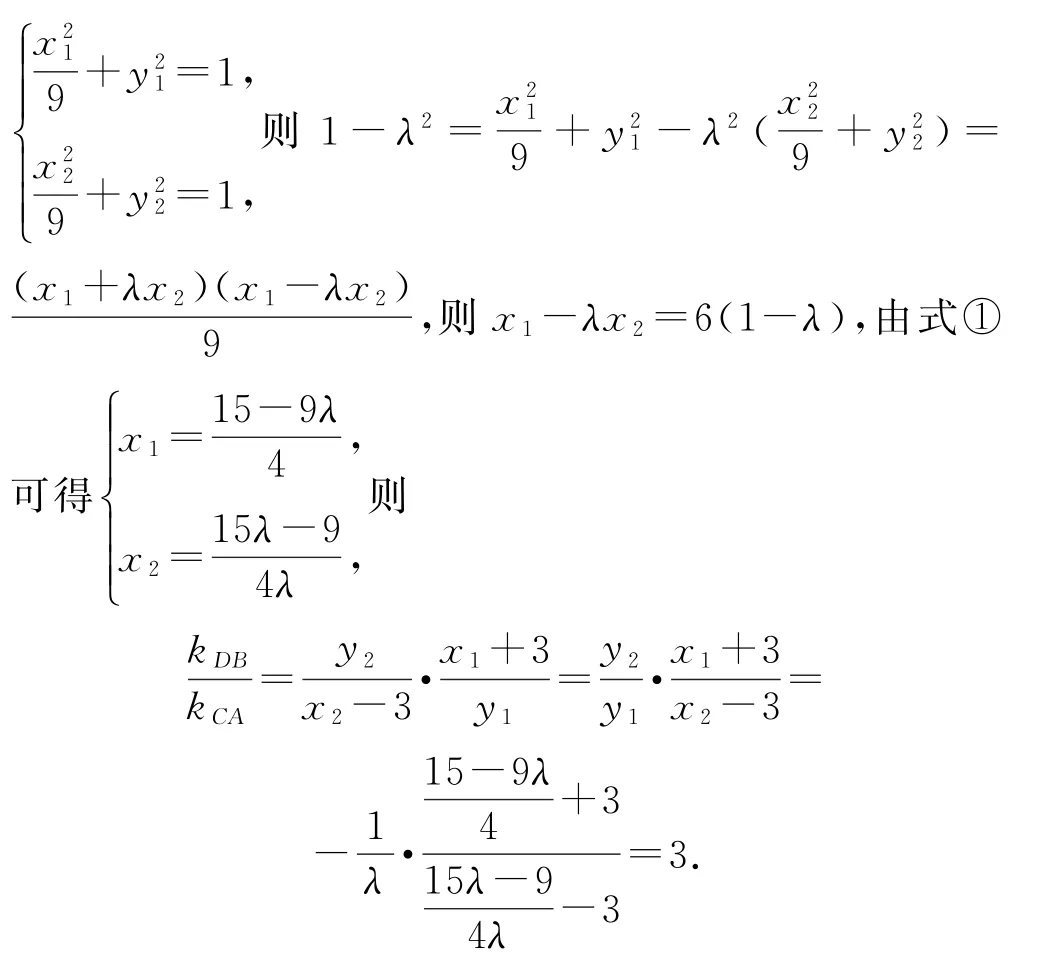
點評

此方法的處理過程中巧妙利用對稱關系,并取特殊位置猜想并計算直線CD經過的定點.本題中由于動點P為主動點,利用斜率kPB＝3kPA的關系變換視角,只要證明直線CD經過定點0)時,滿足斜率kBD＝3kAC.此時A,B不是同一個點,直接設直線,其坐標形式不具備對稱性,難以處理,轉成設C,D的坐標,并利用定比分點尋找坐標之間的關系,根據點C,D在橢圓上(類似“點差法”原理)對式子先進行一次系數乘法后相減直接得到x1＋λx2,x1－λx2,這和定比分點相呼應,利用λ表示x1,x2,可證明kBD＝3kAC成立.

視角3選擇直線CD為主動線,設CD直線方程,并利用兩根的和與積的關系轉化,利用方程思想求解.

解法3設直線CD的方程為x＝my＋n,C(x1,y1),D(x2,y2).聯立方程得

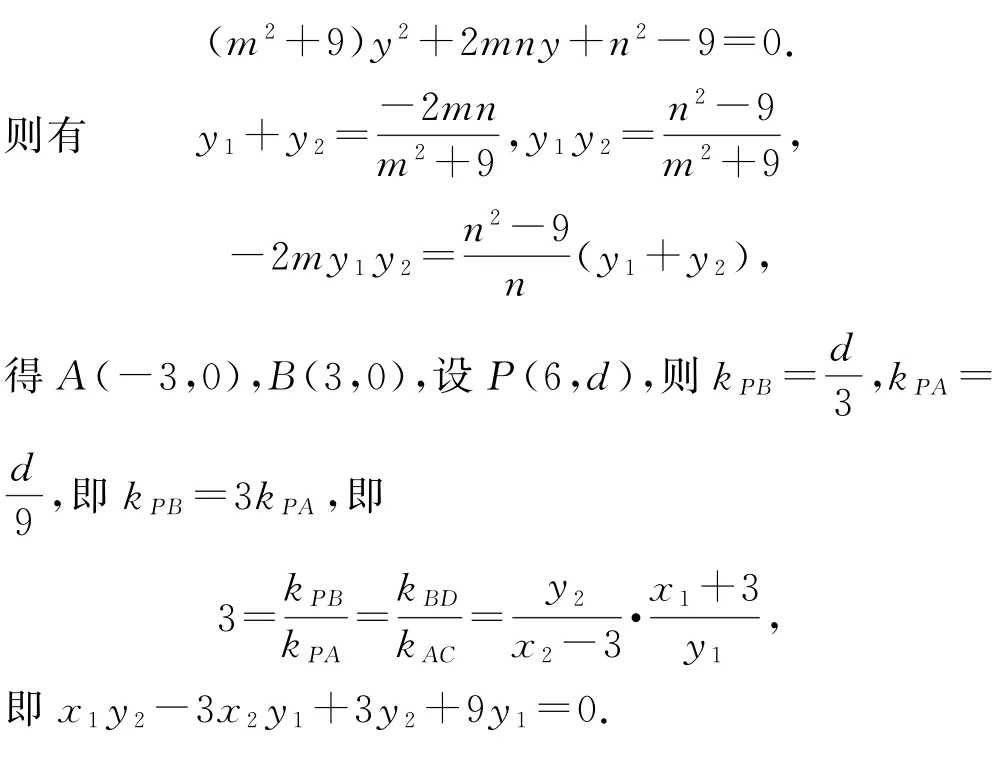
又因為x1＝my1＋n,x2＝my2＋n,整理得

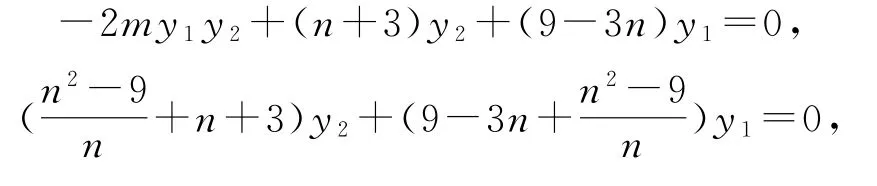
點評

本題動點P為主動點,利用kPB＝3kPA的關系變換視角,視直線CD為主動,設直線CD的方程x＝my＋n,根據斜率之間關系kBD＝3kAC,尋找兩個參數m,n間的等量關系.利用直線代點統一坐標,得出的關系－2my1y2＋(n＋3)y2＋(9－3n)y1＝0不具備對稱性,根與系數的關系難以處理,但注意到式子出現y1y2,和y1,y2,故可以將積y1y2向y1＋y2轉化,從而得到再通過代入即可求出的值.

視角4選擇直線CD為主動線,設CD直線方程,巧用曲線方程代入轉化為對稱.

解法4因為A(－3,0),B(3,0),設P(6,d),C(x1,y1),D(x2,y2).所以3kAP,所以kBD＝3kAC,即

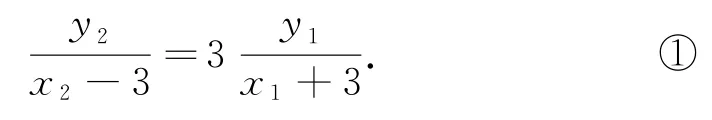
因為C,D在橢圓上,則

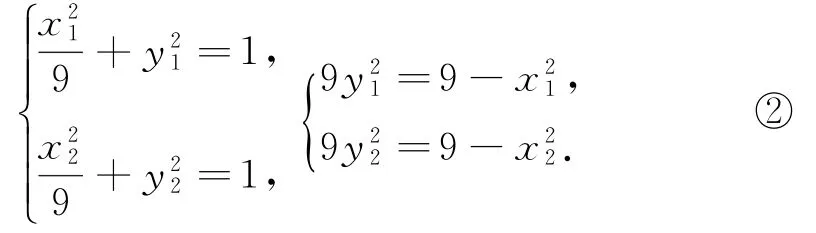
由式①可得

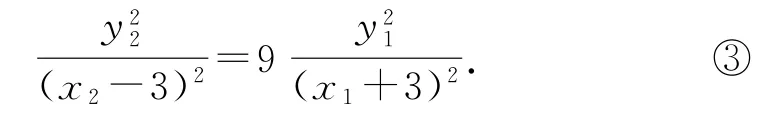
將式②代入式③得

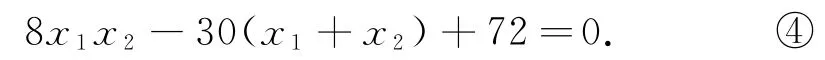
設直線CD的方程為y＝kx＋m,聯立可得

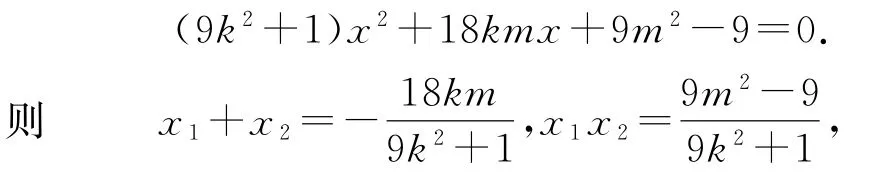
代入式④得

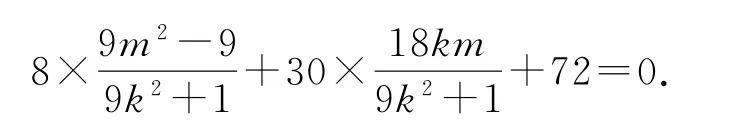
得3k＋2m＝0或m＋6k＝0(此時CD過點(－6,0),不在橢圓內,m＋6k＝0不符合題意),所以直線CD的方程為,即CD過定點.

點評

本題將動點P設為主動點,利用kPB＝3kPA的關系變換視角,設直線CD的方程為y＝kx＋m,根據斜率之間關系kBD＝3kAC.由于A,B不是同一個點,但是它們關于原點對稱,利用曲線上點滿足曲線方程,整體代入,實現了對稱化,利用根與系數的關系求解得到參數k,m之間的關系,從而得到直線CD經過定點.

視角5抓住斜率關系,轉化為同一點斜率的乘積關系,化齊次式處理.

解法5因為A(－3,0),B(3,0),設P(6,d),C(x1,y1),D(x2,y2),則即kPB＝3kPA.由橢圓的第三定義可得則有.

設直線CD的方程為m(x＋3)＋ny＝1,C(x1,y1),D(x2,y2).橢圓方程9,即(x＋3)2－6(x＋3)[m(x＋3)＋ny]＋9y2＝0,即(1－6m)(x＋3)2－6n(x＋3)y＋9y2＝0.兩邊同時除以(x＋3)2,得

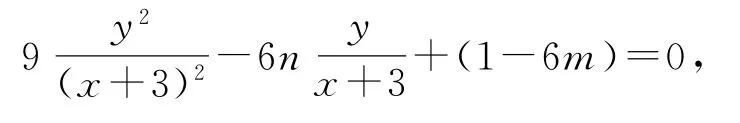
則有

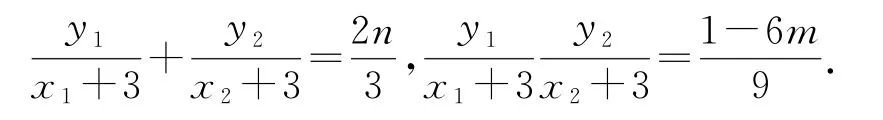
點評

利用kPB＝3kPA的關系變換視角,利用橢圓的第三定義得將其轉化為.其中y1y2計算比較復雜,可構造關于的一元二次方程,再根據根與系數的關系處理.直線CD顯然不過點(－3,0),可設為m(x＋3)＋ny＝1,將橢圓的方程的標準方程變形為(x＋3)2－6(x＋3)×1＋9y2＝0,將式子中的“1”利用直線方程代入得(1－6m)(x＋3)2－6n(x＋3)y＋9y2＝0,實現了二次齊次化,再在兩邊同時除以(x＋2)2,便構造了關于的二次方程,最后通過根與系數的關系求解即可.

5 問題變式

根據極點、極線中的配極原則,共點線的極點必共線,此考題還可以變式為如下.

變式如圖2所示,已知A,B分別為橢圓E:的左、右頂點,G為E的上頂點,作直線與橢圓E相交于C,D兩點,直線AC,BD相交于點P.

(1)求E的方程;

(2)證明:點P在定直線上.

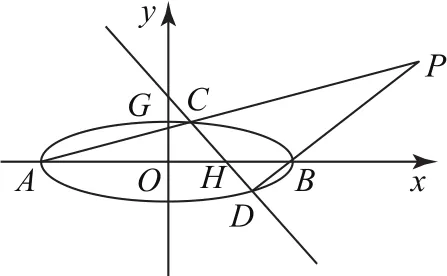
圖2

6 同源真題

(2010年江蘇卷)在平面直角坐標系xOy中,如圖3所示,已知橢圓的左、右頂點為A,B,右焦點為F.設過點T(t,m)的直線TA,TB與此橢圓分別交于點M(x1,y1),N(x2,y2),其中m＞0,y1＞0,y2＜0.

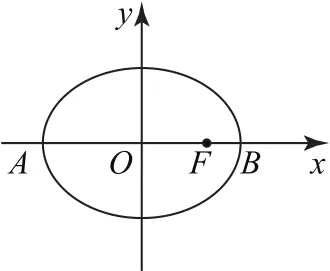
圖3

(1)設動點P滿足|PF|2－|PB|2＝4,求點P的軌跡;

(3)設t＝9,求證:直線MN必過x軸上的一定點(其坐標與m無關).

7 回顧反思

在數學學習的過程中,我們能夠發現一道題目可以用許多方法來解答,此時需要靈活運用條件從多個視角進行思考.本文對2020年的一道圓錐曲線試題進行探究,可知圓錐曲線綜合問題處理途徑主要是圍繞著兩條主線來展開.

1)設點法,針對“多動”問題,尋找主動點,巧設參數,用此參數表示其他相關點,例如解法1和解法2;

2)設線法,針對多條動直線,尋找主動直線,設直線方程處理問題,例如解法3、解法4和解法5.

直線與圓錐曲線的綜合問題是支撐高中數學知識體系的重點內容,同時圓錐曲線問題的解決具有入口寬、方法靈活多樣等特點,用不同的解題途徑,其運算量就有繁簡之分.解析幾何中常常有一類問題,將幾何條件轉化為坐標形式,其關系式子中不含x1＋x2和x1x2,呈現非對稱的特征,會導致運算量增大,本文從多種途徑優化運算.

1)利用曲線上的點滿足曲線方程,整體代入,將非對稱問題轉化為對稱問題;

2)利用兩根和與積之間的關系,將兩根積轉化為和,通過方程思想求解;

3)利用橢圓的第三定義轉換關系,實現對稱化處理;

4)對數學的關系式進行合理構造,利用斜率的積與和之間的關系結合根與系數的關系,將曲線方程轉化為“二次齊次式”,并根據齊次式的特征,將兩變量化為斜率形式,從而解決問題.

波利亞有句名言:“發現問題比解決問題更重要.”在圓錐曲線的教學中,要啟發學生多角度、多層次去思考問題、解決問題,同一個知識點若使用的角度不同、使用的先后順序不同,其效果也就大不一樣.因此我們必須審時度勢、巧妙地運用這些知識點,從而使問題得到簡化,更要引導學生提煉一般模型及解法,達到舉一反三的目的,從根本上提升學生的數學素養.