解析幾何中的“三定”問題解法探究

◇ 山東 馬 英 李冠蘭

解析幾何中的定值、定點、定線問題是歷年高考或各地模擬考試中“常考常新”的熱點問題,就2020年高考而言,全國卷Ⅰ(理科)和新高考卷都進行了考查.這類問題大多在解答之前并不知道定值是什么、定點在什么位置、有怎樣的定直線,考試時遇到這類問題往往讓考生望而生畏、倍感困惑.因此,歸納總結這類問題的題型特點和求解策略實屬必要.

1 定值問題

解析幾何中的定值問題是指某些幾何量(線段的長度、圖形的面積、角的度數、直線的斜率等)的大小或某些代數表達式的值和題目中的參數無關,不依參數的變化而變化,始終是一個確定的值.

解法探究選好參數,求出題目所需的代數表達式,然后對表達式進行直接推理、計算,并在推理計算的過程中消去變量,從而得到定值.這種方法可簡記為:一選(選好參變量)、二求(對運算能力要求頗高)、三定值(確定定值).

例1已知橢圓的左、右焦點分別為F1,F2,|F1F2|＝2,M是橢圓E上的一個動點,且△MF1F2面積的最大值為.

(1)求橢圓E的標準方程;

(2)若A(a,0),B(0,b),四邊形ABCD內接于橢圓E,AB∥CD,記直線AD,BC的斜率分別為k1,k2,求證:k1k2為定值.

解析

(1)設橢圓E的半焦距為c,由題意可知,當M為橢圓E的上頂點或下頂點時,△MF1F2的面積取得最大值所以故橢圓E的標準方程為.

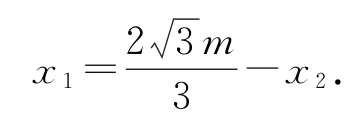
直線AD的斜率為

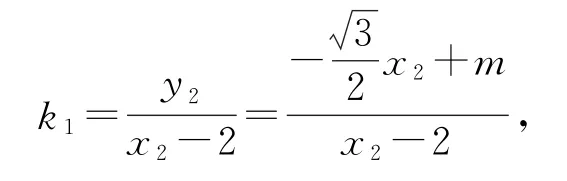
直線BC的斜率為

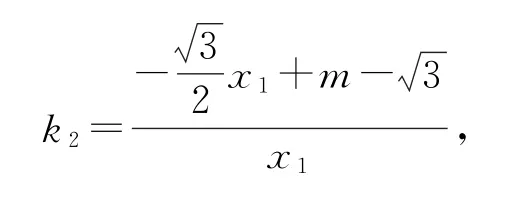
所以

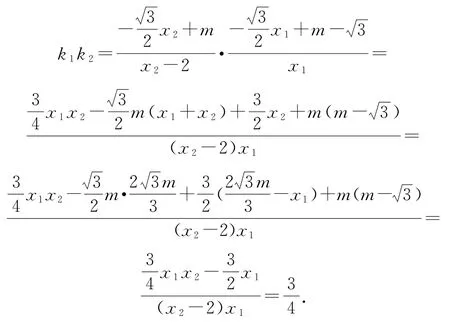
故k1k2為定值.

點評

本題第(2)問選“m”為參數,設出直線CD的方程與橢圓方程聯立,設而不求分別表示出直線AD和直線BC的斜率,然后變形整理,整體消掉含有參數的式子得到定值.考查了考生分析、解決和整體處理問題的能力.

2 定點問題

解析幾何中的定點問題是指直線過定點或曲線過定點問題,即不論直線或曲線中的參數如何變化,直線或曲線都經過某一個定點的問題.

解法探究定點問題的兩種解法:一是從特殊入手,求出定點,再進行一般性的證明;二是把直線或曲線方程中的變量x,y當成常數看待,把相關的參數整理在一起,同時方程一端化為零.既然是過定點,那么這個方程就要對任意參數都成立,這時參數的系數就要全部等于零,這樣就得到一個關于x,y的方程組,這個方程組的解確定的點就是直線或曲線所過的定點.

例2(2020年全國卷Ⅰ理20)已知A,B分別為橢圓的左、右頂點,G為E的上頂點為直線x＝6上的動點,PA與E的另一交點為C,PB與E的另一交點為D.

(1)求E的方程;

(2)證明:直線CD過定點.

解析

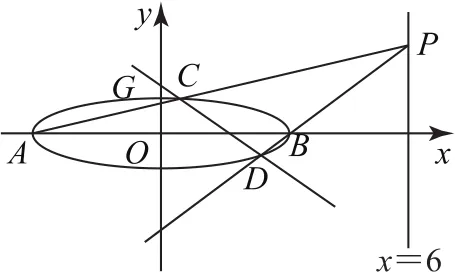
圖1

(2)設P(6,y0),則直線AP的方程為y＝聯立直線AP的方程與橢圓方程可得整理得

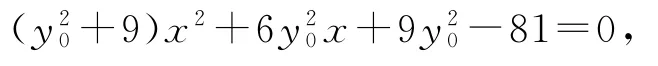
同理,可得點D的坐標為,所以直線CD的方程為

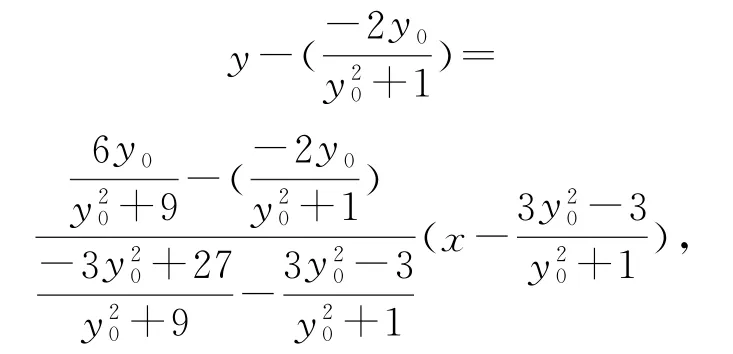
整理可得

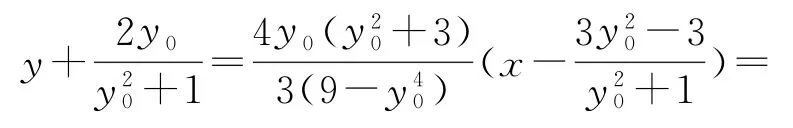
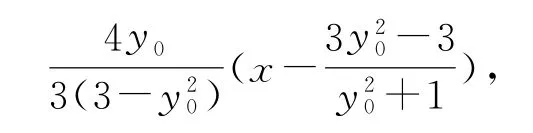
點評

本題第(2)問以點P的縱坐標為參數,得到直線AP的方程后與橢圓方程聯立,整理變形后代入表示出點C和點D的坐標,進而表示出直線CD的方程,確定出與參數無關的定點.本題主要考查了橢圓的簡單性質及方程思想的運用,考查了運算求解能力、推理論證能力及化歸與轉化思想.

3 定線問題

解析幾何中的定線問題是指求證某動點不管如何變化,始終在某條直線上的問題,其本質就是求動點的軌跡方程.

解法探究定線問題是證明動點在定直線上,其實質是求動點的軌跡方程,所以所用的方法就是求軌跡方程的方法,如定義法、消參法、交軌法等.

例3已知橢圓C的方程為斜率為的直線l與橢圓C交于A,B兩點,點在直線l的左上方.

(1)若以AB為直徑的圓恰好經過橢圓C的右焦點F2,求此時直線l的方程;

(2)求證:△PAB的內切圓的圓心在定直線x＝1上.

解析

(1)設直線l的方程為y1),B(x2,y2).由得x2＋mx＋m2－3＝0,則x1＋x2＝－m,x1x2＝m2－3.

由Δ＝m2－4(m2－3)＞0,解得－2＜m＜2.又因為點在直線l的左上方,所以－2＜m＜1.若以AB為直徑的圓恰好經過橢圓C的右焦點F2,則,即

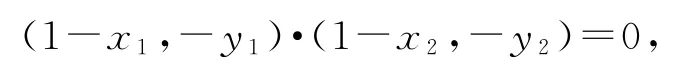
化簡得7m2＋4m－11＝0,解得或m＝1(舍),所以直線l的方程為.

點評

本題第(2)問是通過運算得到兩條直線的斜率的和為0,說明直線x＝1平分∠APB,從而證明△PAB內切圓的圓心在定直線x＝1上.考查了分析、解決問題的能力和數形結合的數學思想.

4 綜合應用

例4(2020年新高考卷22)已知橢圓的離心率為且過點A(2,1).

(1)求C的方程;

(2)點M,N在C上,且AM⊥AN,AD⊥MN,D為垂足.證明:存在定點Q,使得|DQ|為定值.

解析

(2)設點M(x1,y1),N(x2,y2).因為AM⊥AN,所以,即

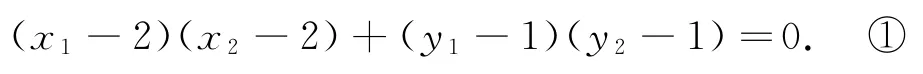
當直線MN的斜率存在時,設方程為y＝kx＋m,如圖2所示,代入橢圓方程消去y并整理得

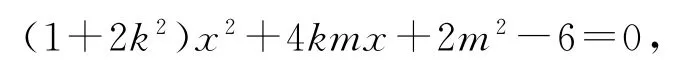
所以

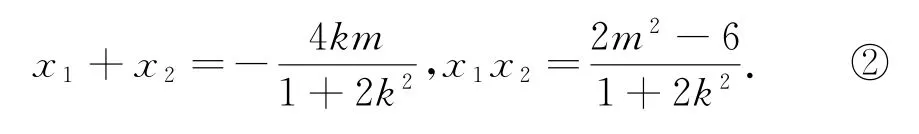
根據y1＝kx1＋m,y2＝kx2＋m,代入①整理得(k2＋1)x1x2＋(km－k－2)(x1＋x2)＋(m－1)2＋4＝0.

將②代入,得

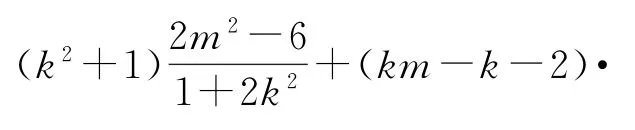
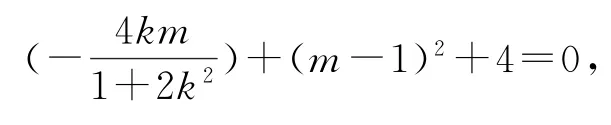
整理化簡得(2k＋3m＋1)(2k＋m－1)＝0.

因為A(2,1)不在直線MN上,所以2k＋m－1≠0,2k＋3m＋1＝0,k≠1,于是MN的方程為,因此直線M過定點.

當直線MN的斜率不存在時,可得N(x1,－y1),如圖3所示.代入式①可得(x1－2)2＋1－,解得x1＝2(舍)或,此時直線MN過點.

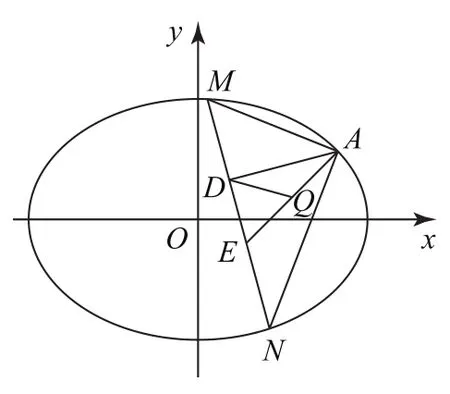
圖2

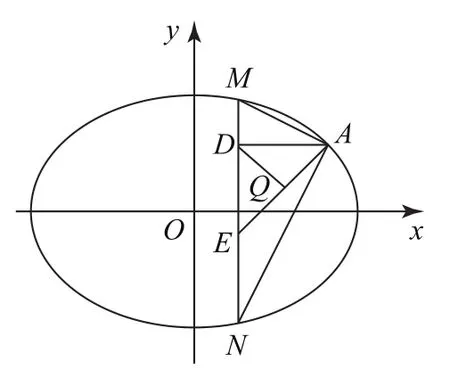
圖3

由于AE為定值,且△ADE為直角三角形,AE為斜邊,所以AE中點Q滿足|QD|為定值(AE長度的一半,即.

點評

本題第(2)問設出點M,N的坐標,在斜率存在時設方程為y＝kx＋m,聯立直線方程與橢圓方程,根據已知條件,得到m,k的關系,進而可知直線MN恒過定點,在直線斜率不存在時要單獨驗證,然后結合直角三角形的性質即可確定滿足題意的點Q的位置.本題考查了橢圓的標準方程和性質,是圓錐曲線中的定點、定值問題,特別是本題第(2)問在探索|DQ|為定值的基礎上證明直線MN經過定點,并求得定點的坐標,考查了考生的理性思維和思維的靈活性、深刻性,方法的綜合性、探究性和創造性等.本題對考生的數學思維能力提出了較高的要求,要求考生具備解決較復雜問題的綜合素養和能力.