基于差分原理的重力壩深層抗滑穩定可靠度研究

李向鵬，王 剛，李夢瑤，秦凈凈

(大連理工大學水利工程學院，遼寧 大連 116024)

0 引 言

抗滑穩定性是混凝土重力壩結構安全評價的關鍵，可靠度方法是結構安全評價的重要方法。可靠度理論已經在水工結構(如重力壩等)的安全評價中得到了廣泛應用，并納入到相關設計規范(標準)中。當前，可以通過計算重力壩的抗滑穩定可靠指標β判斷壩體及基巖是否滿足安全標準[1]。然而，實際工程中很多重力壩壩址工程地質條件復雜，大壩基巖內往往存在錯綜復雜、相互切割交錯的斷層、軟弱夾層、節理裂隙等，這些結構面及其組合會形成壩基深層潛在的滑移通道，其中雙斜面的情況最為典型。另外，當不同壩基滑移通道具有共同結構面或滑移面間存在類似的巖土統計特性時，滑移通道間就會成幾何或物理力學參數的相關性，此相關性如何考慮需要結合具體工程進行專門分析。總體上看，當前研究中較多地關注壩基內不同滑移通道各自的安全度或可靠度，未能對若干滑移通道組合時的情形進行定量分析，從而對基巖整體失穩狀態的評價存在一定不足。因此，有必要基于體系可靠度理論對重力壩基巖內存在若干滑移通道組合的情況開展整體抗滑穩定可靠度分析。

可靠指標β的計算通常采用蒙特卡洛數值模擬(MC)方法、驗算點法、響應面法等[2]。其中，MC法[3- 4]屬于隨機抽樣方法，為了保證計算精度，需要模擬大量的隨機樣本，計算效率非常低；響應面法通過多次迭代運算擬合功能函數，并多在功能函數為隱式時采用，當功能函數的非線性較強、變量之間相關性較高時，計算誤差較大，且可靠指標計算在驗算點處產生振蕩[5]；驗算點法，如中心點法、一次二階矩法(FOSM)等，屬于數學近似方法，精度低于MC法，且需要功能函數為顯式表達以便于計算中求解功能函數的偏導數，一般而言效率較高。另外，體系可靠度理論在重力壩結構安全分析中也得到了應用，如寬窄界限法、主次結合法、史蒂文森-莫謝斯法等[4]，多是用于大壩滿足強度、穩定等不同使用功能時的綜合分析，而直接針對本文問題的研究并不多見。

為更好地解決重力壩深層抗滑穩定計算中功能函數為隱式且非線性程度高的問題，綜合考慮各種可靠度計算方法的優缺點和適用性，本文提出將數值差分原理引入到SORM法中，通過差分方法求解功能函數的偏導數，進而計算抗滑穩定可靠指標；在研究壩基深層多滑移通道穩定體系可靠度時，先將不同滑移通道視為單一失效模式，再結合各滑移通道可靠指標計算結果采用寬窄界限法計算重力壩基巖整體抗滑穩定體系可靠度。將此計算方法應用到基巖地質條件復雜、存在多條滑移通道的典型重力壩工程案例中，并采用MC法進行精度和適用性驗證。

1 基于差分原理的可靠度計算方法

1.1 功能函數偏導數的差分計算

由于二次二階矩法中求解關于各隨機變量X=(X1，X2，…，Xn)的偏導數時，需要功能函數Z=g(X)為顯式形式，而實際工程中可靠指標β計算時常遇見Z為隱式函數的情況。數值差分法是求解隱式函數偏導數的有效方法。蘇永華[6]等詳細推導了二維空間內利用差分理論求解函數導數的計算公式，基于差分原理可以得到驗算點X0處的功能函數對各變量的一階偏導數和二階偏導數，如式(1)～(3)所示。

(1)

(2)

(3)

式中，λ為步長；為了使偏導數計算具有較高的精度，λ取值應盡量小，文獻[7]建議在0.03～0.01之間取值。

1.2 基于差分原理可靠指標 β的計算

考慮變量間相關性時，求解β過程包括以下幾個步驟：

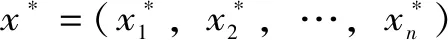
(5)按相關系數矩陣ρY產生下三角矩陣A，并按式(1)～(3)的形式計算功能函數的一階偏導數向量gY(y*)和二階偏導數矩陣2gY(y*)；從而計算單位向量

(4)

(6)以αY′第n列向量由Gram-Schmid方法確定正交矩陣H′，并計算矩陣Q′，即

(5)

(7)經過簡化可得二次二階矩法對應的失效概率Pf及修正后的可靠指標β如下

(6)

β=Φ-1(1-Pf)

(7)

式中，Φ為正態累積分布函數。

2 體系可靠度計算

2.1 失效模式間相關性

失效模式間的相關性往往對系統可靠度分析結果產生較大影響，所以在進行結構體系可靠度分析時，必須考慮這種相關性。基于上述方法，由式(4)在驗算點收斂處，求得第i、j個失效模式中隨機變量xk的敏感性因子αik、αjk，兩者之間的相關系數為

(8)

由式(8)可知，兩個失效模式間的相關性系數與兩個功能函數中共同隨機變量的數目以及驗算點處的敏感性系數大小有關，共同隨機變量敏感性系數越大，數目越多，相關系數就越大，兩個失效模式間相關性也越高。

2.2 寬窄界限法

寬窄界限法[9-10]是計算體系可靠度的常用方法，但界限法并不能直接計算可靠指標，需要先由其他方法求得體系內每個子系統的可靠指標及它們之間的相關系數，然后明確每個子系統相互之間的串并聯關系，進而使用界限法計算體系可靠指標。

1967年，Comell在文獻中提出串聯系統失效概率Pf的寬界限為

(9)

式中，Pfi為第i個失效模式的失效概率。

1979年特里文森(Ditevsen O)對式(9)進行了改進，提出窄界限法計算公式即

(10)

式中，P(Ei∩Ej)為兩個失效模式同時失效的概率。

對于重力壩基深層抗滑穩定問題，巖基內的每一條滑移通道(失效模式)視為一個子系統，整體壩基失穩體系即由若干子系統根據失穩性質串聯構成，同時，每個滑移通道又由若干單元(即滑移面)并聯構成，這樣重力壩基巖整體穩定體系可靠度模型是一個串并聯系統，可以先由本文介紹的基于差分原理的可靠度方法計算各滑移通道的可靠指標，明確失效系統內構件間得邏輯關系后，再采用寬窄界限法計算整個基巖的抗滑穩定體系可靠指標。本文的單一滑移通道考慮最為典型的雙斜面情形。

3 工程實例

某重力壩上游水位92.0 m，下游水位22 m。計算選取的擋水壩段壩頂高程102.00 m，壩頂寬5.5 m。揚壓力折減系數在為0.25，帷幕距壩踵7.5 m。上游壩面豎直，下游壩坡在94 m高程以下坡度為1∶0.75，在94 m高程以上豎直。主滑面傾角α=16.4，滑面傾角β=27.0。根據已知兩條滑移通道的資料，對該重力壩的基巖整體穩定可靠度進行分析。巖基整體穩定計算剖面見圖1。

圖1 巖基整體穩定計算剖面

3.1 單滑移通道可靠度計算

根據文獻[11]，可使用等安全系數法構建多斜面情況下的可靠度計算極限狀態方程，此時極限狀態方程為復雜的非線性方程組，安全系數K是隱含在方程組中的未知數，常規驗算點法難以解決該問題，因此，采用本文提供方法計算，并采用MC法進行驗證，模擬抽樣次數為300萬次。

巖基抗滑穩定極限狀態方程為

(11)

式中，i、j為滑移面編號，其中，i=1、2，j=3、4。∑W為壩體的豎向作用總合；∑P為壩體的水平作用總和；f′1、f′2分別為滑動塊ABD和BCD的摩擦系數；c′1、c′2分別為滑動塊ABD和BCD的黏聚力；U1、U2、U3分別為滑裂面AB、BC和BD的揚壓力；γ1、γ3分別為重力壩和水容重；G1、G2分別為滑裂面ABD和BCD的重力；Q為BD的抗力；Ψ為BD的抗力與揚壓力U3的夾角。

可令K1=K2代入式(11)求得K，功能函數Z=K-1，顯然Z為非線性隱式函數。

該工程重力壩基巖4個滑裂面如圖1所示，4個滑移面可組合形成四組雙斜面滑移通道，編號分別為：Ⅰ(A1B-BC1)，Ⅱ(A2B-BC1)，Ⅲ(A1B-BC2)，Ⅳ(A2B-BC2)。可靠度計算時，隨機變量取結構面的抗剪斷摩擦系數f′和粘聚力c′。結合實際工程地質力學參數及以往研究中抗剪斷參數的統計特征[12]，4個滑移面的f′與c′的隨機分布特性見表1。

表1 基巖結構面參數的統計特征

抗剪斷參數f′與c′一般呈負相關性，單滑移通道可靠指標計算時考慮兩種情況：相關系數ρ=0(不相關)和ρ=-0.3(相關)。由于隨機參數分布類型不同，故本文可靠度計算中采用Nataf變換對參數相關性進行處理，最終計算結果見表2。

表2 2種方法計算成果比較

圖2 算法收斂過程

從表2可以看出，參數相關性對可靠指標β影響顯著，考慮參數相關性后，可靠指標計算值較不相關情況要大。另外，對4個失效模式根據可靠指標大小排序(見圖2)。由圖2可知，不考慮相關性時排序為Ⅱ<Ⅰ<Ⅲ<Ⅳ，而考慮相關性時排序為Ⅱ<Ⅲ<Ⅳ<Ⅰ，兩種情況存在一定差異。

本文方法計算結果與MC法相對誤差在2%～4%之間，MC法可靠指標計算值均略高于本文方法，總體上計算精度相當。可見，本文方法可以解決隱式非線性功能函數可靠度計算問題，且由圖2可看出，在計算過程中迭代次數為9～31之間，計算效率相比MC法大為提高。

3.3 體系可靠度計算

根據式(8)計算滑移通道間相關性見表3。

表3 相關系數計算結果

當相關系數為0時，說明兩滑移通道間無共同滑面，如I和Ⅳ、Ⅱ和Ⅲ等；相關系數為1時表示完全相關；當兩相關滑移通道間的共同滑面為主動滑面(靠近壩踵)時，相關系數均大于共同滑面為被動滑面(靠近壩址)的情況。

本文方法得到的基巖整體抗滑穩定可靠度計算結果如表4所示，表中一并列出MC法的計算結果，便于進行對比分析。

表4 體系可靠度計算結果

從表4可以看出，窄界限法計算得到的可靠指標β區間范圍較寬界限法窄，寬界限法區間范圍包含了MC法可靠指標計算值，幾種方法均滿足工程精度需要。可見本文方法具有較好的應用價值。

4 結 論

本文將差分原理應用到可靠度二次二階矩法中，并結合體系可靠度寬窄界限法對重力壩基巖整體抗滑穩定可靠度進行了研究，計算結論如下：

(1)本文方法在計算可靠指標時，能兼顧精度和效率，并可較好地處理對于功能函數為隱式非線性的情況。

(2)結合工程實例進行計算時，本文方法可以考慮隨機變量的不同分布類型和變量間的相關性，計算結果符合一般規律。

(3)在實際工程中，重力壩基巖深層多滑移通道構成的復雜滑移體系是較為常見的情形，本文方法可以更為全面地分析重力壩基巖多條滑移通道整體可靠度，從而為重力壩抗滑穩定安全分析的進一步研究提供有力的技術支持，也為重力壩壩基抗滑穩定性研究提供新的思路。