基于MATLAB的輪胎側偏剛度對汽車瞬態響應影響研究

吳云兵，胥峰，李兵，熊樂，張鵬飛，應宇汀

（中汽研汽車檢驗中心（寧波）有限公司，浙江 寧波 315336）

前言

汽車的操縱穩定性是指在駕駛員不感到過分行、疲勞的條件下，汽車能遵循駕駛員通過轉向系及轉向車輪給定的方向行駛，且當遭遇外界干擾時，汽車能抵抗干擾而保持穩定行駛的能力[1]。汽車瞬態響應特性是指瞬態狀況下的運動響應，一般分為時域響應特性和頻率響應特性。時域響應特性一般是基于角階躍輸入下瞬態響應，頻率響應特性可以用橫擺角速度的增益和相位角表示。

輪胎受力狀況、運動狀態以及與路面間的相互作用復雜性極大增加了輪胎力學特性研究的難度[2]。而輪胎的側偏剛度又是輪胎的重要力學參數之一，對整車操縱穩定性有重要影響。因此，研究不同輪胎側偏剛度對汽車瞬態響應的影響，對提高整車操縱穩定性有著重要意義。

本文通過建立線性二自由度汽車模型的橫擺角速度傳遞函數，并利用 MATLAB編寫角階躍輸入瞬態響應試驗仿真程序，研究了不同輪胎側偏剛度對汽車前輪角階躍輸入瞬態響應的影響。

1 輪胎的側偏特性

輪胎的側偏特性是輪胎力學特性的重要組成。側偏特性主要是指側偏力、回正力矩與側偏角之間的關系，它是研究汽車操縱穩定性的基礎。

輪胎坐標系與地面反力的關系如圖1所示。垂直于車輪旋轉軸線的輪胎中分平面稱為車輪平面。坐標系的原點O為車輪平面和地平面的交線同旋轉軸線在地面上投影的交點。車輪平面與地平面的交線為X軸，規定向前為正。Z軸與地平面垂直，規定指向上方為正。Y軸在地平面上，規定面向車輪前進方向時指向左方為正。

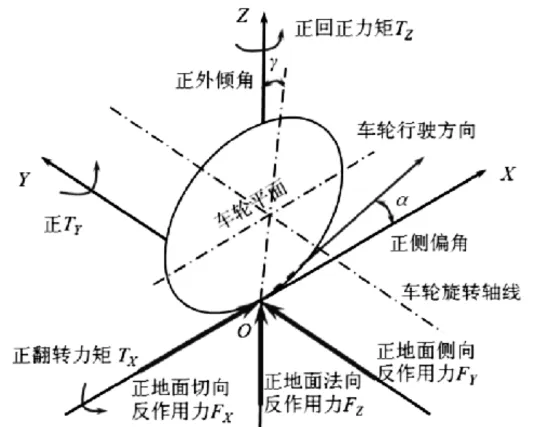
圖1 輪胎的坐標系與地面反力

由于汽車行駛過程中常受到傾斜路面、離心力及側風等因素的影響，當側向力FY未到達附著極限的時候，車輪前進方向偏離車輪平面，上述便是輪胎的側偏現象，側偏角α即為車輛前進方向與車輪平面的夾角。試驗結果顯示，當側偏角不超過 5°時，側偏力FY與側偏角α為線性關系。汽車正常行駛時，側向加速度小于 0.4g，側偏角不大于 4°～5°，便可將側偏力FY與側偏角α的關系當做線性關系，即：

式中：k為輪胎側偏剛度。

2 整車二自由度動力學模型

為便于掌握操縱穩定性的基本特性，通常將車輛簡化成一個由前后兩個有側向彈性的輪胎支撐于地面、且只具有側向及橫擺運動的二自由度汽車模型。

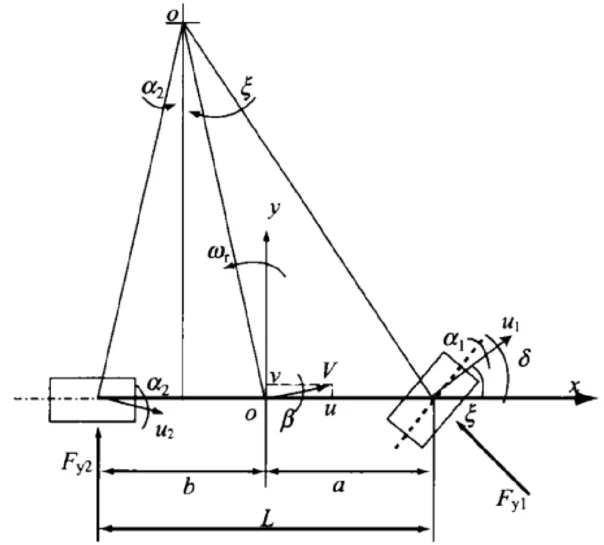
圖2 二自由度汽車模型

當車輛側向加速度值限制在0.4g范圍內時，輪胎側偏特性呈現線性關系。在車輛坐標系下，根據二自由度汽車沿y軸方向受力及繞質心的力矩情況，得到線性二自由度汽車運動微分方程為：

式中：k1、k2分別為前輪和后輪的側偏剛度；a、b分別為汽車質心至前、后軸的距離；β為質心的側偏角，且β=u/v；u、v；分別為質心速度V在車輛坐標系x、y軸上的速度分量，即縱向車速和側向車速；ωr為汽車橫擺角速度；δ為前輪轉角；m為汽車質量；IZ為汽車轉動慣量。

由式（2）可得：

對式（3）求導可得：

將式（4）代入式（2）得：

式（5）寫成以ωr為變量的形式，即：

式（6）是單自由度一般強迫振動微分方程式，通常寫成：

當給定前輪的輸入為轉角盤角階躍輸入，其數學表達式為：

當t＞0時，式（8）進一步簡化為：

3 動力學模型的解析

微分方程（9）為二階常系數非齊次，顯然它的通解為它的對應的齊次微分方程的通解與特解之和。其特解為：

當K=0時，此時車速與橫擺角速度與成比例關系，該狀態稱為中性轉向（見圖3）。

當K＞0時，較中性轉向時偏低，車速與其不再呈現比例關系，此時的橫擺角速度增益曲線低于中性轉向，當汽車具備這種特性時便稱作不足轉向。當K值增大時，橫擺角速度增益的曲線逐漸降低，不足轉向量增加。車速達到的時候，橫擺角速度增益的數值達到最大。uch稱為特征車速，對汽車不足轉向有著重要影響。

當K＜0時，較中性轉向時偏高，此時的橫擺角速度增益曲線高于中性轉向，當汽車具備這種特性時便稱作過多轉向。當K值增大時（即K值的絕對值增大），帶來更大的過多轉向。車速達到的時候，車輛轉向靈敏度值趨近無窮大，ucr被稱作臨界車速，對車輛過多轉向量有著重要影響。臨界車速減小時，帶來更大的過多轉向。

圖3 橫擺角速度增益曲線

式（10）對應的齊次方程為：

其通解可由如下的特征方程求得：

根據ζ的數據，特征方程的根為：

齊次方程的通解為：

上式中，積分常數 C、Φ、C1、C2、C3、C4的值需依照車輛的初始條件來計算。

當ζ＞1時，橫擺角速度ωr(t)為持續增長的，為大阻尼。當時間持續推進時，ωr逐步接近穩態橫擺角速度ωr0；一旦車輛速度超過其臨界車速ucr，ωr便趨于發散，接近無窮大，該狀態下車輛失穩。

當ζ=1時，橫擺角速度ωr(t)曲線也是持續增長的且趨近ωr0，稱作臨界阻尼。

當ζ＜1時，橫擺角速度ωr(t)是為減幅正弦曲線，且最終收斂于值ωr0，其瞬態響應為小阻尼。現代生產的汽車的瞬態響應通常為小阻尼，因此本論文只探討前輪在轉向盤角階躍輸入下，ζ＜1時狀態下ωr(t)的變化規律，研究影響ωr(t)的結構參數。當ζ＜1時，其橫擺角速度為：

或

下面確定積分常數C、A1、A2。

車輛的起始運動條件是：當t=0，ωr=0，v=0，δ=δ0。根據運動方程式（2）能夠得到t=0的時候，

由于t=0時，ωr=0，求得式（17）中的一個積分常數為：

由于t=0時，，可求得另外一個積分常數為：

而

因此

圖4 轉向盤角階躍輸入下的汽車瞬態響應

式（22）便是當車輛前輪給定轉向盤角階躍輸入裝填下的橫擺角速度瞬態響應。根據車輛的初始條件能夠德奧，當t=0，ωr=0。由式（22）可知，t=∞時，也就是橫擺角速度ωr(t)最終趨近穩態橫擺角速度ωr0。隨著t在0與∞之間變化，ωr(t)為一條正弦曲線，且是逐漸衰減的（見圖4）。很明顯地，當阻尼比增加，衰減速度加快。

影響瞬態響應的參數交通，通常使用以下幾個參數來確定車輛瞬態響應品質，以下描述部分參數。

（1）波動時的固有頻率ω0

根據方程式（7）能夠得到：

固有頻率ω0是評價車輛瞬態響應的重要特征參數之一。當ω0值相對高些時，車輛瞬態響應好。所示為部分歐洲及日本轎車的穩定性因素 K值與固有頻率f0值關系，固有頻率f0=ω0/ 2π。從圖5能夠看見，f0值為1Hz附近時。歐洲高速公路允許的最高車速最高，所以轎車行駛車速高，其固有頻率也較高，在0.9Hz以上[3]。

圖5 部分歐洲及日本轎車固有頻率f0值與穩定性因素K值

（2）阻尼比ζ

由式（7）可知：

計算表明，隨著車速的提高，ζ值減小；在穩定性因素K值不變的條件下，后輪胎側偏剛度增加有助于ζ值得增大；質量、轉動慣量、軸距減小，ζ值亦有所增加[4]。

德國幾個大學的研究機構進行了規模較大試驗，得出的結論是現代轎車超調量是ωrmax/ω0×100%=112%～165%，試驗條件是31.3m/s（70mile/h），ay=0.4g。與此相對應的阻尼ζ=0.5～0.8[5]。

（3）反應時間τ

反應時間為車輛前輪輸入轉向盤角階躍運動后，橫擺角速度第首次到達穩定值ωr0所需時間。也有部分文獻取到達0.9ωr0或0.63ωr0值需要的時間，被用來進行定性分析時，沒有本質區別。τ也是評價車輛瞬態響應重要特征參數之一。τ值偏小時，車輛瞬態響應較好。

加下來把車輛橫擺角速度響應方式（16）重新列出：

當t=τ時，

即sin（ωτ+Φ）=0

故

研究表明：當車速增長時，車輛的響應時間減小；當車輛質量增大時，軸距伸長，車輛的響應時間也相應減小；但轉動慣量增加時，車輛響應時間有所增加。

（4）達到第一峰值ωr1的時間ε

車輛到達第一峰值ωr1所需時間ε通常也被用作評定車輛瞬態橫擺響應品質的特征參數。ε也稱作峰值反應時間。

式（16）兩邊同時取導數，得到：

當t=ε時，

故

德國幾所大學的車輛研究機構進行了轉向盤角階躍響應試驗，得到下面的統計數據：近代車輛的ε=0.23～0.59s；而質心側偏角與峰值反應時間的乘積εβ，即汽車因素 T.B.為0.25～1.45s（°），相應的試驗工況為 31.3m/s（70mile/h），ay=0.4g。Benz中型貨車裝備不同輪胎時，在u=20m/s，ay=0.3g的試驗條件下，ε=0.94～1.72s，T.B.=2.06～4.76s（°），質心側偏角β=2.05°～3.03°。

4 模型的仿真分析

對式（6）進行拉氏變換可得：

經整理得到：

方程式（28）可以被當作控制系統中的傳遞函數，也及時把車輛當作一個開環系統。車輛方向盤轉角δ是輸入激勵，車輛橫擺角速度ωr是輸出響應。式（28）即為汽車系統的傳遞函數。

二自由度汽車車身參數如表1所示。

選取試驗車速為30m/s，在仿真時間為0時給前輪一個階躍信號，使前輪由 0°轉到 10°，并保持不變。為考察輪胎側偏剛度對汽車瞬態響應的影響，前、后輪側偏剛度由－23140N/rad、-38320N/rad變為－33120N/rad、-66250N/rad。

表1 二自由度汽車模型仿真參數

圖6 轉向盤角階躍輸入下的汽車瞬態響應

根據汽車橫擺角速度傳遞函數，編寫繪制不同側偏剛度下的汽車橫擺角速度的時域特性曲線的MATLAB程序。運行程序，得到不同輪胎側偏剛度下的汽車橫擺角速度時域特性曲線如圖 6所示。可以看出，汽車在行駛速度相同、前輪轉角輸入相同的情況下，較大的輪胎側偏剛度，橫擺角速度峰值變化不大，但汽車響應時間顯著縮短，汽車穩定性變好。

5 結論

本文介紹了輪胎的側偏特性，建立了汽車二自由度動力學模型，并對動力學模型進行了求解，最后應用 MATLAB對動力學模型進行了仿真分析。仿真結果表明：較高的輪胎側偏剛度（指絕對值），能顯著縮短汽車響應時間，保證汽車具有良好的操縱穩定性。