學科內統整視角下初中數學復習課設計與思考
徐文良 劉志昂


摘 要:復習課是初中數學教學的重要環節和形式,本文從學科統整的視角對復習課進行設計,對學生的知識、方法和經驗進行統整,旨在以知識為載體,以能力為目標,以統整為手段,發展學生的“四基四能”,落實數學學科核心素養,實現數學的育人價值。
關鍵詞:數學復習課;學科統整;四基四能
中圖分類號:G633.6????????? 文獻標識碼:A???? 文章編號:1992-7711(2020)19-127-2
學科統整,又稱課程統整,課程整合、課程綜合化等,是指經由課程設計的統整,以達成經驗的統整、知識的統整和社會的統整。
初中數學復習課便是一個很好的統整契機,因而,作為老師,我們應該有統整的意識,在統整的理念下進行復習課的設計。
一、基于知識的統整
在數學復習課的設計中,教師應始終以整體聯系的眼光組織、設計和處理各章節、各單元和各知識點的聯系,讓學生在整體中、在聯系中、在比較中學習,從而幫助學生在頭腦中將知識“豎成線,橫成片”,或“由點構成線,由線構成面”,形成立體、開放、整體的知識結構。
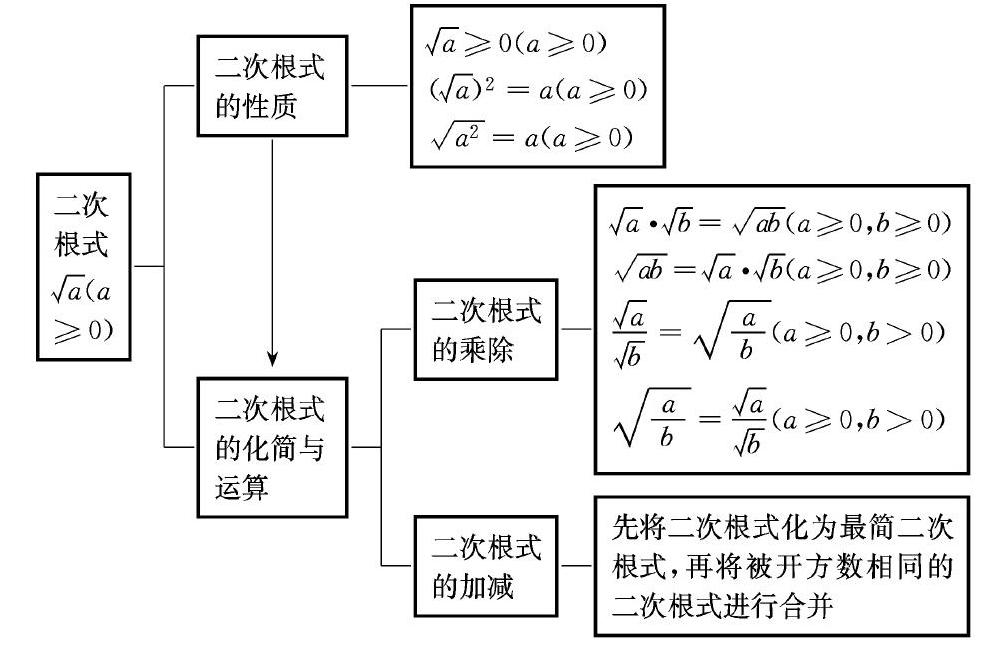
在章節復習課中,則主要是對于本章節知識的一個回憶、梳理和歸類,同時找出知識之間的內在聯系。如《二次根式》的復習,不妨設計出如下的知識框圖來進行表述。
二次根式a(a≥0)
二次根式的性質
a≥0(a≥0)(a)2=a(a≥0)a2=a(a≥0)
二次根式的化簡與運算
二次根式的乘除
a·b=ab(a≥0,b≥0)
ab=a·b(a≥0,b≥0)
ab=ab(a≥0,b>0)
ab=ab(a≥0,b>0)
二次根式的加減
先將二次根式化為最簡二次根式,再將被開方數相同的二次根式進行合并
在專題復習課中,要側重對相近知識、關聯知識的統整。例如《中點四邊形》的專題復習課中,一定是統整線段的中點、三角形的中位線等概念,以及三角形中位線定理、平行四邊形的判定定理、矩形、菱形和正方形的判定定理等。
二、基于方法的統整
在知識聯系為綱的統整的同時,數學的學習方法和經驗也是在不斷的積累、反思、改進中融會貫通的,其本身也是一個漸近的、呈螺旋式上升的過程。這種學習方法的掌握、學習能力的提升需要教師在不同的時期、不同的階段和學生一起對之進行統整。
如在《正方形中的互垂線段》專題復習課中,可以這樣設計:
如圖1,ABCD是一個正方形花園,E、F是它的兩個門,且CE=DF。要修建兩條路AE和BF,這兩條路等長嗎?它們有什么位置關系?為什么?
解析:這是一道實際生活背景下的幾何題。將CE=DF轉化為BE=CF,運用“SAS”證明△ABE≌△DAF,得到AE=BF和∠BAE=∠CBF,再進一步證明AE⊥BF,得到線段之間的特殊位置關系——垂直、特殊數量關系——相等。
1.互逆變式
探尋原命題的逆命題是否成立——簡單的說,就是將題設中的部分已知條件與部分結論交換,形成新的命題,探尋是不是真命題。
變式1.如圖1,在正方形ABCD中,點E、F分別在BC、CD上,且AE⊥BF,垂足為M,那么AE與BF相等嗎?證明你的結論。
變式2.如圖,在正方形ABCD中,點E、F分別在BC、CD上,且AE=BF,那么AE與BF垂直嗎?證明你的結論。
2.在正方形中進行變式
變式3.如圖2,正方形ABCD中,如果點E、F、G分別在BC、CD、DA上,且GE⊥BF于點M,那么GE與BF相等嗎?證明你的結論。
變式4.如圖2,正方形ABCD中,如果點E、F、G分別在BC、CD、DA上,且GE=BF,那么GE與BF垂直嗎?證明你的結論。
變式5.如圖3,正方形ABCD中,如果點E、F、G、H分別在BC、CD、DA、AB上,且GE⊥HF,垂足M,那么GE與HF相等嗎?證明你的結論。
變式6.如圖3,正方形ABCD中,如果點E、F、G、H分別在BC、CD、DA、AB上,且GE=HF,那么GE與HF垂直嗎?證明你的結論。
顯然,這里都是原題的變式,都是通過平行移動來完成條件的轉化,最終化歸為原問題來解決。解決問題的根本辦法都是通過證明全等三角形,利用全等三角形的性質來證明。
三、基于經驗的統整
經驗統整既是綜合科學課程的統整屬性之一,也是處理科學教材組織問題的第二種基本視角。在學生不斷學習和發展的過程中,新學習的經驗要與既有的經驗在交互作用中不斷整合起來,學生的經驗由此不斷生長,人格也不斷完善。筆者認為,科學教學中的經驗統整即學生在科學學習過程中所實現的新舊科學知識經驗的整合,通過科學探究活動方式對學科知識經驗進行統整是一種重要的經驗統整方式。
如在單元專題復習課《一次函數背景下的三角形面積》中這
樣設計:
例1 一次函數y=2x-4的圖像如圖4所示,求△OAB的面積。
問題1:三角形的面積公式是什么?△OAB是什么三角形?它的底和高分別是什么?如何求OA和OB的長?如何求點A和點B的坐標?
例2 將圖4中的直線y=2x-4圍繞著點A按照逆時針方向旋轉(如圖5),交y軸于點C(0,2)。
問題2:圖中有幾個三角形?它們可以如何分類?面積分別是多少?
例3 將圖5中的直線AC沿著x軸的方向向左平移3個單位(如圖6),分別交x軸于點D,交y軸于點E。
問題3:圖中的三角形中,哪些與前面的三角形不同?它們的面積分別是多少?其面積的求法與前面的三角形有沒有共性?
例4 將圖6中的y軸向右平移4個單位長度,分別與原來的兩條直線交于點G和H(如圖7)。
問題4:是否存在與圖6中不同的三角形?如何求它們的面積?
例5 將圖7中的直線GH圍繞著點H按逆時針旋轉,與直線AB交于點M(如圖8),已知點M的縱坐標為1,求△FHM的面積。
問題5:求這個三角形的構成與前面的三角形是否一樣?如何去求其面積呢?在解決這些問題的過程中,你有哪些感悟和體會?
本課例的設計,不僅僅是一個逐漸一般化的過程,也是一個解題經驗的逐漸積累和形成的過程,更是一個解決問題的過程。這里既有對過去經驗的組織和統整,也有新經驗的不斷加入并統整到意義的系統中,實現和新舊經驗的整合,形成新的、有價值的經驗,并為解決后續的相近、相似問題,積累了寶貴的基本活動經驗。
在解決這些問題的過程中,也逐漸構建了一個解決問題的模式——在一次函數背景下的三角形,充分利用坐標軸或與坐標軸平行的直線來求其面積。而例5則需要通過作輔助線,用“割”或者“補”的辦法,轉化為上述模式中的三角形來解決,這是對上述模式的識別與應用,也促進了基本活動經驗的螺旋式上升。
綜上所述,初中數學復習課的設計,應以知識為載體,以能力為目標,以統整為手段。在知識、能力和經驗的統整中,使學生理解和掌握基本的數學知識與技能、數學思想和方法,獲得基本的數學活動經驗。體會數學知識之間、數學與其他學科之間、數學與生活之間的聯系,運用數學的思維方式進行思考,增強發現和提出問題的能力、分析和解決問題的能力。
[參考文獻]
[1]余文森.核心素養導向的課堂教學[M].上海:上海教育出版社,2017.
基金項目:江蘇省“十三五”教育科學規劃重點自籌課題——初中生認知能力發展的學科統整研究(Eb/2018/13)
(作者單位:蘇州高新區第三中學校①;蘇州高新區第五初級中學校②,江蘇 蘇州215000)

