輪荷轉移條件下前束值對操縱穩定性的影響分析

勞俊 謝偉忠 劉夢巖 何家興 王瑞林

（廣州汽車集團股份有限公司汽車工程研究院，廣州 511434）

主題詞：操縱穩定性 前束值 不足轉向度 輪荷轉移

1 前言

車輛轉向過程中，其響應需符合駕駛員的意愿。出現響應慢、穩定性差等問題時，通常從轉向系統、懸架系統K&C和輪胎等方面進行分析。而車輪前束值常被認為與車輛跑偏、輪胎磨耗關系較大[1]。左、右輪相等的前束值產生的側向力能相互抵消，因此前束值常被忽略[2-3]，有涉及前束的研究，但因未建立參數化的數學模型以及缺少輪胎側偏剛度與垂直載荷間關系的描述，所以均無法準確解釋機理[4-5]。車輛在轉彎過程中，內、外輪存在輪荷轉移[6]，而對應的輪胎側偏剛度也因輪荷的變化而產生左、右差異，形成某方向的側向力，從而影響整車橫擺角速度和側向加速度的變化，最終影響整車操縱穩定性。

本文從軸荷轉移的角度定量分析車輛前束角對整車操縱穩定性的影響。采用參數化的二自由度操縱穩定性模型，從機理上解釋前束值與操縱穩定性指標間的關系，得出定量的敏感度系數，并通過仿真和試驗進行驗證。

2 前束值影響機理分析

2.1 線性二自由度模型

對某線性二自由度簡化車輛模型進行研究[7]。分析過程中，忽略轉向系統的影響，直接以前輪轉角作為輸入，忽略懸架的作用，認為汽車車廂只作平行于地面的平面運動。在本文特定仿真與試驗設計下，汽車沿X軸的速度u視為不變，忽略輪荷轉移造成的側偏力影響和外傾側向力、輪胎回正力矩、輪胎錐度力、路面斜度等的影響。因此，上述系統只有沿Y軸的側向運動以及繞Z軸（以質心為原點）的橫擺運動2個自由度。前、后輪的側向受力關系如圖1所示。

沿車輛側向（Y向）建立力的平衡方程：

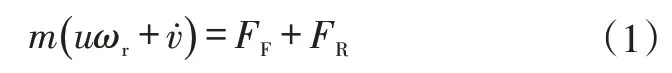
式中，m為整車質量；ωr為擺臂角速度；為側向加速度；FF、FR分別為前、后輪側偏力。

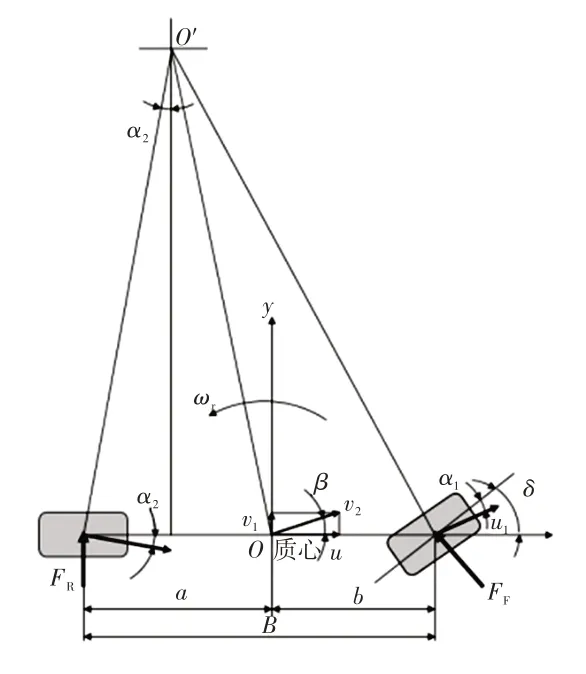
圖1 二自由度汽車模型

在車輛的橫擺方向，力矩的平衡方程為：

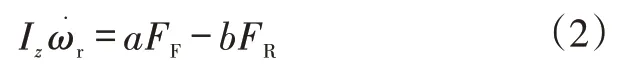
式中，Iz為整車沿質心橫擺方向的轉動慣量；a、b分別為質心到前、后軸的距離。

輪胎的側偏力表達式為：

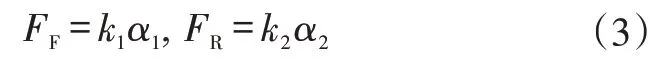
式中，α1、α2分別為前、后輪的側偏角；k1、k2分別為前、后輪的等效側偏剛度。

車輪實際的側偏角由輪胎側偏角與懸架側偏角組成，如圖2a所示。如圖2b、圖2c所示，在懸架的作用下，前、后輪的轉向角分別出現負前束（Toe out）和正前束（Toe in），對前、后輪的實際側偏剛度造成影響，等效側偏倍率分別為

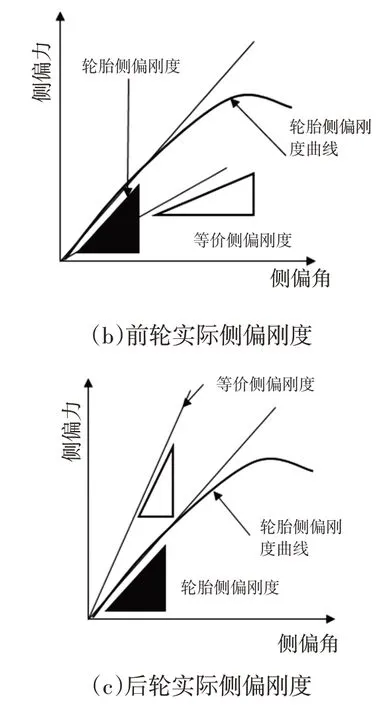
圖2 等效側偏剛度

前、后輪側偏角分別為：

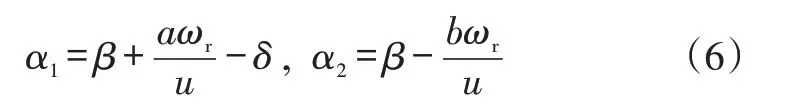
式中，β=v/u為質心的側偏角；δ為前輪轉角。

整理后得到二自由度汽車運動微分方程為：

穩態時，橫擺角速度ωr為定值，此時代入式（7）、式（8）得：

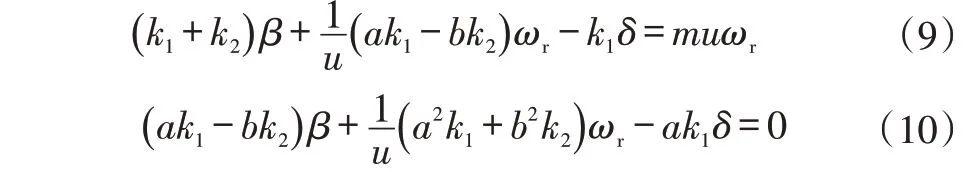
此時整車側向加速度為ay=uωr，將兩式聯立消去β，可求得穩態不足轉向度為：

但前輪轉角在試驗中難以測量，故測量轉向盤轉角δsw。轉向盤不足轉向度為：

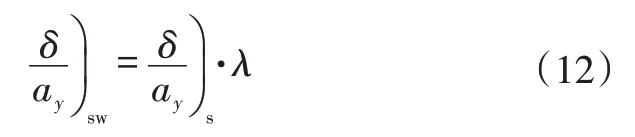
式中，λ為轉向盤與前輪間的轉向傳動比。

通過該模型可計算未考慮前束作用時的不足轉向度。例如，采用某款轎車A與某SUV車B的整車參數進行計算，如表1 所示，其中，H為質心高度，tF、tR分別為前、后輪單邊前束角，L為整車軸距。

表1 車輛A和車輛B的參數

分別計算得出車輛A 和B 前軸C1分別為0.74%、0.73%，C2分別為103%、102%。因此，通過式（12）可求得車輛A 和B 的轉向盤端的不足轉向度分別為24.62(°)/g、25.18(°)/g。

以上模型雖表征了車輛的穩態響應狀態，前、后輪都采用單輪進行簡化，因此前束角均被抵消，而且沒有考慮輪荷轉移的情況。如需考慮前束角的影響，前、后輪必須考慮雙輪，且需考慮輪荷轉移。

2.2 改進后的線性二自由度操縱穩定性模型

輪胎側偏剛度隨載荷的增加而增大。車輛A 輪胎采用六分力測試設備在滾動狀態下測得不同垂向載荷下側偏角與側偏力關系曲線，如圖3所示。

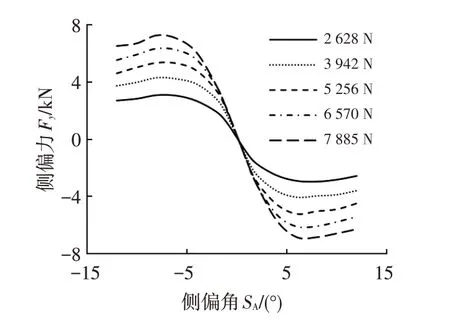
圖3 某輪胎不同垂向載荷下側偏角與側偏力關系曲線

因只考慮0.4g以下的工況，只關注輪胎Fy/SA的線性段。通過對輪胎曲線的性能段進行擬合求出側偏剛度，如圖4所示。

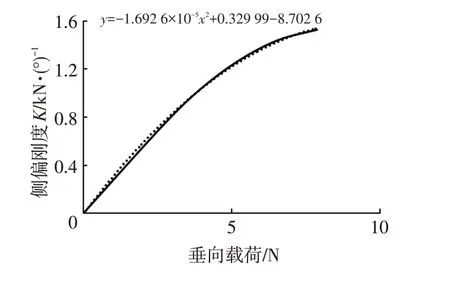
圖4 垂向載荷與側偏剛度（線性段）

通過二次三項式擬合近似表達垂向載荷與側偏剛度的關系，以左前輪側偏剛度為例：

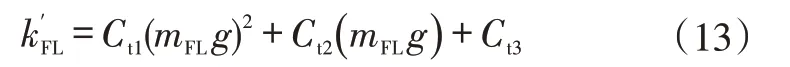
式中，Ct1、Ct2、Ct3分別為二次三項式的擬合系數；mFL為左前輪輪荷質量。

在以上二自由度模型以及輪胎載荷與剛度的擬合公式基礎上對汽車模型進行改進，提出以下前提：前輪左、右轉角一致，前束絕對值一致；只考慮輪荷轉移，不考慮側傾，如圖5所示；前、后軸的質心高度、輪距、側向加速度、胎壓均一致；側偏剛度為線性，隨載荷的變化也擬合為二次三項式非線性。模型如圖6所示。

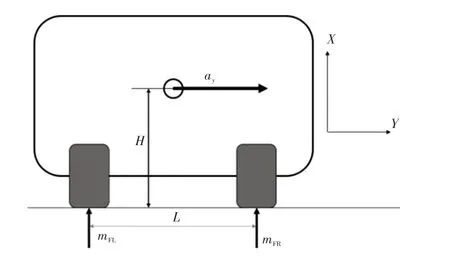
圖5 側傾方向的受力平衡與輪荷轉移

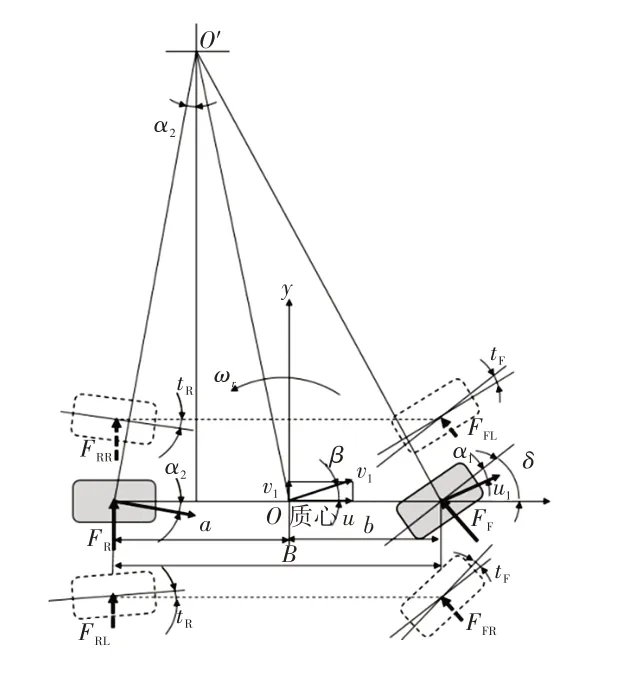
圖6 改進后的二自由度汽車模型

因左、右輪轉角相同，通過受力分析，有：

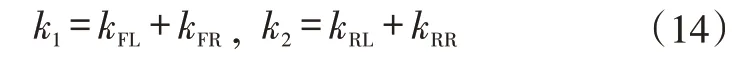
式中，kFL、kFR、kRL、kRR分別為左前、右前、左后、右后輪側偏剛度。

側傾方向的平衡方程為：

式中，ay為側向加速度；mF、mR分別為前、后軸荷質量；mFR、mRL、mRR分別為右前輪、左后輪、右后輪輪荷質量。

以左前輪為例，單個車輪的側偏力為：

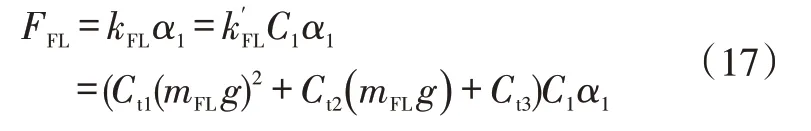
由式（24）可知，前束對不足轉向度的影響量與tF和tR前的系數相關，將此系數稱為敏感度系數T。T與H、L、mF、mR、Ct1、Ct2、有關，與C1、C2無關。

因側偏剛度為負值，所以當前輪單邊前束tF負向絕對值增加時（Toe in），不足轉向度會下降，車輛趨向轉向過度；后輪單邊前束tR負向絕對值增加時（Toe in），不足轉向度會上升，車輛趨向轉向不足。

已知車輛A 和B 的Ct1=-1.692 6×10-5N·(°)-1，Ct2=0.329 9(°)-1，參考表1中的參數，計算可得不足轉向度和敏感度系數如表2所示。

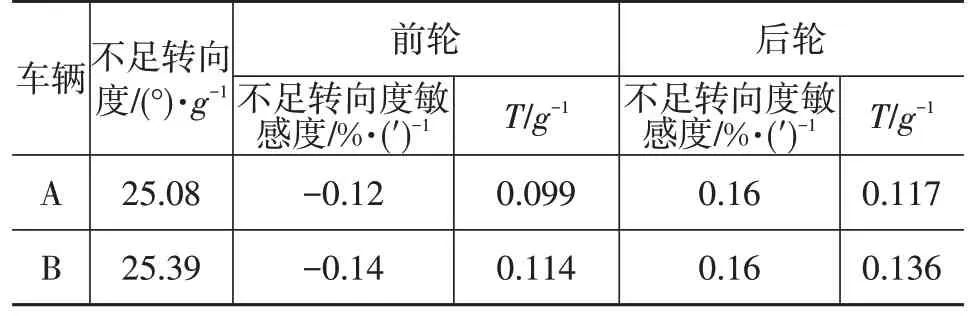
表2 不足轉向度與前束敏感度

考慮前束作用后，不足轉向度有所提升。后懸架的敏感度系數T較高。車輛B 較車輛A 敏感，與車輛B 質心較高有強相關性。

3 仿真分析

3.1 仿真模型與工況

3.1.1 仿真模型

采用ADAMS-CAR模塊進行分析，如圖7所示，前、后懸架按已有產品車輛A和車輛B進行搭建，均為前麥弗遜式、后四連桿式，車身為剛體，按前排2人，后排1人進行配重。輪胎模型為PAC 模型，采用在六分力測試設備上獲得的純側偏力（見圖3）、純縱向滑移力、接地水平面扭轉剛度、接地水平面垂向/側向/縱向的剛度、斜置滾動側向力等曲線擬合取得。

圖7 操縱穩定性仿真模型

3.1.2 仿真工況

穩態回轉工況：車輛行駛在半徑為40 m 的軌跡圓上，起步后緩慢而均勻地加速（側向加速度增量不大于0.2 m/s3），同時調整轉向盤使車輛保持在固定的半徑軌跡圓上，半徑允許公差為±0.5 m），直到車輛不能保持在圓周上行駛為止。數據處理：截止頻率為15 Hz，將單個方向0～0.4g下的數據用最小二乘法線性擬合，并求得算術平均值后得到車輛線性范圍內的轉向盤轉角梯度，即不足轉向度。本文二自由度模型中采用車輪轉角梯度進行分析，但考慮實車試驗難度，采用轉向盤轉角梯度替代分析。此時，轉向盤轉角與車輪轉角間近似恒定地相差轉向系統的傳動比倍率。

頻率掃描試驗工況：車輛在100 km/h車速下勻速行駛在平直路段，從中間位置起緩慢連續進行轉向盤正弦輸入，頻率范圍為0.2～0.3 Hz。數據以100 Hz采樣率導出并計算傳遞函數得到頻域曲線，在曲線上讀取0.5 Hz下的橫擺角速度與轉向盤轉角的增益。

按照表3所示的工況調整前束角，分析其對上述整車參數的影響。

3.2 仿真結果

仿真結果如表4、表5所示。

將穩態不足轉向度除以中值前束的結果，前、后懸架前束中值平移歸零，可輸出敏感度趨勢如圖8所示。

表3 前束變化情況 (′)

表4 前輪前束穩態與瞬態仿真結果

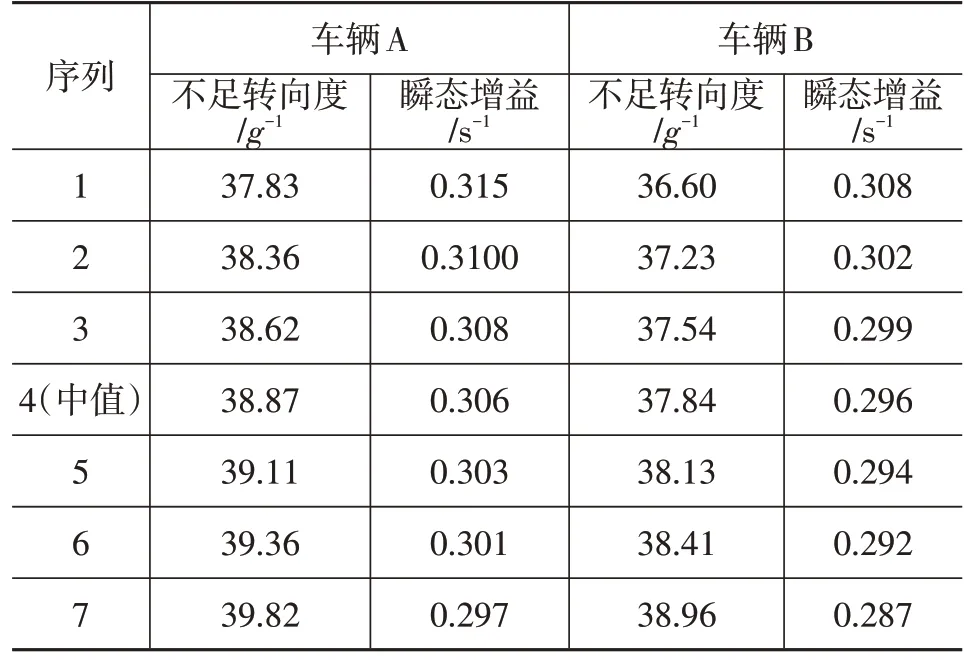
表5 后輪前束穩態與瞬態仿真結果

圖8 前束的不足轉向度影響敏感度

由圖8可知，車輛A與B的前輪前束增大時，不足轉向度均減小，后輪前束增大時，不足轉向度均增大，趨勢與二自由度模型相符。另外，從2個車型的不足轉向度趨勢看，后輪的敏感度較前輪高。

采用上述同樣的處理方法可得瞬態橫擺角速度增益試驗結果如圖9所示。由圖9可知，瞬態增益與不足轉向度顯現相似的趨勢。前輪前束增大時，橫擺增益增大，后輪前束增大時，橫擺增益減小。同樣，從2個車型的增益趨勢看，后輪的敏感度較前輪高。

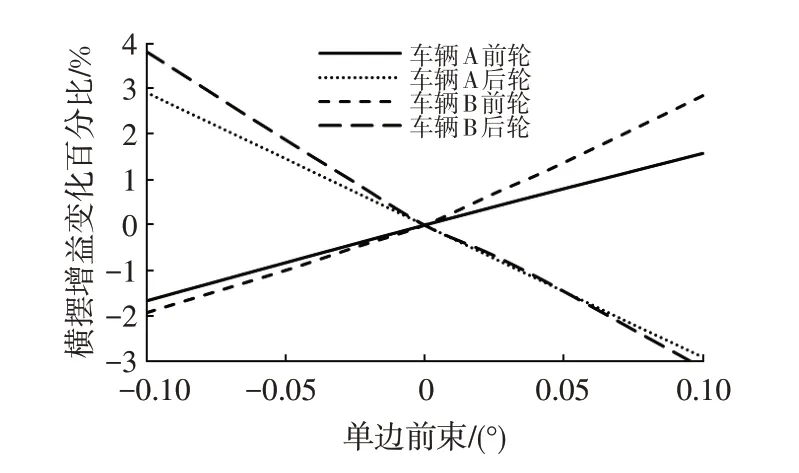
圖9 前束的瞬態橫擺增益影響敏感度

按單位前束角變化相應參數的變化比例計算前束敏感度，結果如表6所示。

表6 前束敏感度 %·(′)-1

ADAMS 計算的敏感度趨勢與2.2 節中的簡化模型相同，2種計算結果中車輛B的敏感度較車輛A大，后軸較前軸更敏感，證明仿真結果同樣符合簡化模型的敏感度預期。其中數值的差異是簡化模型中輪胎與懸架模型省略了較多變量所致，如轉向系統剛度、輪胎扭轉剛度、外傾角、外傾角梯度等。

4 操縱穩定性試驗驗證

采用車輛A 進行試驗驗證，按照與仿真相同的工況、配重條件進行試驗。因實際前束調整需要在四輪定位儀上完成，操作較為繁復，故只進行5組試驗。其中，前懸架調整前束時外傾角變化可忽略。含有偏心螺栓的前束臂與后下臂的多連桿后懸架在調整前束時外傾角有較大變化，需要同時微調前束臂與后下臂的長度，以在調整前束變化的同時，保持外傾角不變。試驗矩陣如表7所示。

在進行穩態試驗與瞬態試驗后，整理數據可得前、后輪的單位前束角敏感度：前輪不足轉向度為0.12%·(′)-1，瞬態增益為0.20%·(′)-1；后輪不足轉向度為0.16%·(′)-1，瞬態增益為0.26%·(′)-1。可見，前、后輪前束變化時，整車響應的趨勢與仿真結果相同，且也顯現出后輪敏感度較前輪高的趨勢，該趨勢可以用2.2節得到的敏感度系數T進行預測。但從數值上看，實車的穩態后輪前束敏感度較仿真結果高，但瞬態結果較仿真低。這與車輛的車身剛度、后懸K&C實際參數相關。

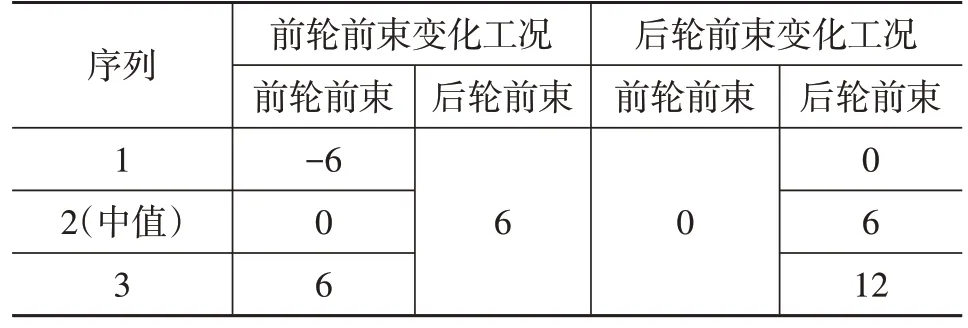
表7 前束變化矩陣 (′)

5 結束語

本文從二自由度操縱穩定性模型出發，研究了靜態前、后輪單邊前束值的對穩態和瞬態的影響機理，前輪前束值的增加會降低穩態不足轉向度，提升瞬態增益，后輪則相反，且敏感度高于前輪。最后通過仿真和試驗驗證了其正確性。通過量化敏感度的方式，為設計前束值及其公差提供了參考依據。

由敏感度系數T與質心高度的強相關性可知，降低質心高度可以有效降低前、后前束的敏感度，使前束設計可以更有利于其他性能，如偏磨、燃油經濟性等。另外，前、后軸荷也影響前、后前束的敏感度，所以，降低前、后軸荷比值可以有效提升后輪前束的敏感度，更有效提升整車操縱穩定性。因為敏感度的不同，前、后不同的前束匹配會影響操縱穩定性。前輪前束對加速跑偏等影響較大，所以在操縱穩定性設計時，按后輪前束值大于前輪的方式進行匹配設計，可有效提高穩定性而不影響其他性能，此方式特別適用于質心較高，且前軸質量較大的SUV車型。

前束值影響輪胎偏磨、整車經濟性及滑行距離，故調校時可在相應性能敏感度較低或允許的范圍內，調整對應的前束值達到提升操縱穩定性的目的。同時，對于敏感度較高的后輪，可作為重點的調整方向。