挖掘教材價值 培育數學思維之花
——小學數學教學中學生數學思維能力培養的策略

江蘇省鹽城市第一小學教育集團聚亨路校區 劉海萍

教材呈現的是靜態的基本素材、基本內容和基本方法，教師在教學時應充分挖掘學生身邊的暗含著某種數學現象或數學規律的數學問題，關注學生的障礙點和發展點，引導學生用數學方法描述變量之間的數量關系。蘇教版《義務教育教科書·數學》六年級上冊第42 頁思考題，主要是讓學生在探索和應用計算規律的過程中，體會分數乘法中存在的一些有趣現象，發展學生的數學思維能力，感受數學的結構美，激發學生學習數學的興趣。我在教學時既基于教材又高于教材，使靜態的文本材料演示成動態的教學過程，真正體現為學習而教，為生長而教。結合這道“思考題”，我做了精心的設計，開發成一節有梯度的思考題專題課。教學設計環環相扣，層層遞進，引導學生深度學習，培養學生深度思維，體現了探索精神，真正促使學生形成數學素養。

一、基于經驗，讓學生的思維有根

杜威指出：“一盎司的經驗勝于一噸的理論，只是因為在經驗中，任何理論才具有充滿活力和可以證實的意義。”數學的學習要基于學生已有的知識經驗和認知水平，基于學生已經具備的基礎知識、基本技能。規律的探究要以經驗為根系、以舊知為土壤，讓經驗之根更深。

片段一：喚醒經驗，導入新課

出示四道計算題。

請學生口答每道題的結果。追問：運用什么方法可以使計算簡便？

小結：整數的運算律和一些性質對于分數同樣適用，巧用運算律和性質可以使計算更加簡便。其實，分數運算中的技巧還有很多，今天這節課我們就來研究分數運算中的巧算。

【思考】通過口答四道簡便計算題，我讓學生再一次感受整數中的運算律和一些性質在分數計算中可以使計算簡便，引出分數運算中的巧算，喚醒學生已有的經驗，引發學生對分數運算中的技巧的探究興趣，揭示本節課的研究課題。

二、基于方法，讓學生的思維有干

小學生學習數學是一個思考的過程，思考是學生學習數學認知過程的本質特點，是數學的本質特征。可以說，沒有思考就沒有真正的數學學習。在平時的教學中，我發現：學生能夠發現看似簡單的算式背后隱藏的規律，但是卻不能利用規律解決復雜的分數運算，究其原因，是因為解決這類問題時只注重了“巧”的教學，而忽略了“理”的教學。在課堂教學中，我試圖在學生的學和思上做文章，在課堂中引發學生思考，讓學生自主探究，把學生的思維引向深處。學生理解了規律形成的原因，發展學生的符號意識，體會分數運算中存在的一些有趣的現象和數學規律的探究方法，積累了探索經驗，學生的思維順著枝干發展，生長出了嶄新的枝葉。

片段二：探究規律，解決問題

（一）探究規律

出示思考題。學生口算，提問：仔細觀察，你有什么發現？同桌互相說一說。

思考：是不是所有的分數都有這樣的規律呢？為什么分子是1，分母是相鄰自然數的兩個分數會有這樣的計算規律呢？

學生結合算式解釋規律形成的原因，再舉例。

明確：因為這兩個分數的分母是相鄰的兩個自然數，所以在求差時，它們的公分母就是這兩個數的乘積，即求差的分母和求乘積的分母相等；再觀察它們的分子，由于分子是1，所以兩個分數的分子就是相鄰兩個自然數的差（也就是1），與積的分子相等。

引導學生用簡潔的方式表示發現的規律，并利用發現的規律說出一組得數相等的式子。

（二）應用規律

出示：

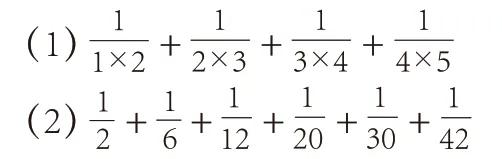
提問：仔細觀察這兩道題，有什么特點？利用通分的方法能解決嗎？

小組討論：有什么好的辦法？能否利用我們發現的規律來解決？

揭示：像這樣，把一個分數拆成兩個分數相減的形式，然后再進行計算的形式，叫作拆分法。

變式練習：

（三）回顧反思

提問：回顧我們剛才的學習過程，是怎么研究的？

小結：從簡單的算式入手，觀察算式的特點，發現隱藏的規律，并應用規律解決問題。

【思考】通過一組有價值的口算，產生研究需求和研究素材。引導學生通過計算、觀察、比較，發現算式背后所隱藏的規律。引發思考：為什么分子是1，分母是相鄰自然數的兩個分數會有這樣的計算規律，理解了規律形成的原因。并適時引導學生用數學符號語言來表示規律，發展學生的符號意識。接著，利用規律說出一道得數相等的式子，加深學生對數學算式中的規律的理解，體會分數運算中存在的一些有趣的現象，這是對規律認識和理解的拓展，對學生思維的要求更進一步。再通過討論交流，自主嘗試，并匯報交流，揭示復雜的分數運算可以運用規律利用拆分的辦法轉化成簡單的運算。加數由少變多，由完全直觀到部分直觀，對學生想象能力、分析能力提出了較高的要求。我最后組織學生進行了有效的回顧與反思，使學生對數學規律的探究方法有了清晰的認識，也為接下來的探究提供了方法，積累了經驗。

三、基于數學思想，讓學生的思維開花

數學思維的訓練要有機滲透數學思想方法。怎樣才能既在數學教學中滲透數學基本思想，又能注意在數學思想的滲透時做到自然貼切、不露痕跡？在教學設計中，教師要恰當把握數學思想的滲透，提升學生的數學素養，讓學生的思維“開放出嬌艷的花朵”。

片段三：回顧反思，深化理解

出示：

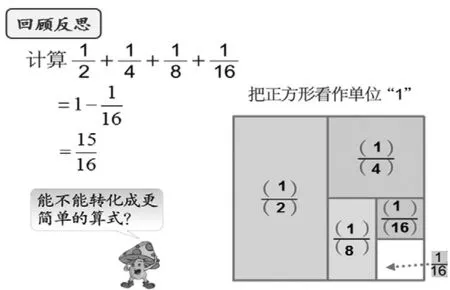
回顧：這是我們五年級的時候做過的一道題，我們原來是怎么解決的？

小結：把算式和圖形聯系起來，也就是數形結合思想的運用。

引發思考：這道分數計算的算式有什么特點？利用拆分的辦法如何解決？

【思考】通過回顧五年級解決過的數學計算題，揭示無論是用拆分的方法還是數形結合的方法，都可以把復雜的算式轉化成簡單的算式來解決，學了新方法，不忘老方法。我在帶領學生探索規律并運用規律解決問題的過程中，有機滲透了等值轉化、數形結合等數學思想。

四、基于數學文化，讓思維之花更艷

興趣是學習的前提，是思維的動力。數學文化的滲透，可以激發學生學習數學的興趣。通過介紹“埃及分數”，滲透數學文化，讓學生了解“埃及分數”與所學知識的關系，并進一步拓展延伸，鼓勵學生課后進一步研究有關“埃及分數”中所隱藏的知識和規律，學生的思維之花更加艷麗。

片段四：總結全課，文化滲透

交流：通過今天的學習，你有哪些收獲？

引出“埃及分數”，埃及同中國一樣，也是世界上著名的文明古國。人們在考察古埃及歷史時注意到像阿基米德這樣的數學巨匠，居然也研究過“埃及分數”。原來古代埃及人沒有幾分之幾的概念，在他們的心目中，當東西分不出整數個時，就先分出幾分之一，再分出幾分之一，古埃及人很早使用的分數都是分子是“1”的分數，所以分子是“1”的分數稱為“埃及分數”。

【思考】計算教學，以知啟智。數學教學的核心目標是培養學生的思維能力，通過計算發展學生的創新思維，這既是計算教學的重要目標，也是數學教育的永恒追求。我試圖通過思考題的教學研究，彰顯思考題的教學價值，讓學生在有梯度的引導下，經歷思考的過程，將學生的思維引向深處，使學生的數學思維在課堂中生長。借助這個載體讓學生感悟、掌握其中的思考元素，從而獲得更有意義的思維發展，這樣的課堂才會展現出數學教學最本真的價值。