鄰域近似條件熵的特定類屬性約簡及啟發(fā)算法
牟 恩,張賢勇,姚岳松,鄧 切
1.西南醫(yī)科大學(xué) 醫(yī)學(xué)信息與工程學(xué)院,四川 瀘州646000
2.四川師范大學(xué) 智能信息與量子信息研究所,成都610066
3.四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,成都610066
1 引言
粗糙集屬性約簡能夠有效實(shí)施降維優(yōu)化與規(guī)則推理[1]。傳統(tǒng)“決策分類約簡”追求所有決策類的全局優(yōu)化,而Yao和Zhang[2]提出的“特定類約簡”涉及特定類的局部優(yōu)化,兩類屬性約簡分別位于決策表的宏觀高層與中觀中層[3]。當(dāng)前,特定類約簡主要立足于經(jīng)典粗糙集[4-5],故值得推廣。鄰域粗糙集推廣了經(jīng)典粗糙集,但相關(guān)屬性約簡集中于決策分類約簡(如文獻(xiàn)[6-7]),還未見特定類約簡的報(bào)道。
信息度量廣泛應(yīng)用于不確定刻畫與屬性約簡。對于經(jīng)典粗糙集,苗奪謙[8]建立信息熵、條件熵、互信息體系,而條件熵刻畫了屬性約簡[9-10]。對于鄰域粗糙集,Hu等[11]建立對數(shù)函數(shù)信息體系進(jìn)行特征選擇,Chen等[12]提出鄰域精度、鄰域熵、信息粒度及相關(guān)粒化單調(diào)性,Chen等[13]利用聯(lián)合鄰域熵來設(shè)計(jì)基因選擇算法,Yuan等[14]采用鄰域熵變種度量來進(jìn)行離群點(diǎn)檢測;進(jìn)而針對屬性約簡,謝玲玲等[15]提出近似條件熵來進(jìn)行屬性約簡,張寧和范年柏[16]提出鄰域(近似)條件熵來構(gòu)建啟發(fā)式屬性約簡,趙小龍和楊燕[17]提出鄰域粒化條件熵來設(shè)計(jì)增量約簡算法,姚晟等[18]基于鄰域粗糙互信息來進(jìn)行非單調(diào)屬性約簡。
本文擬從鄰域近似條件熵的信息角度,構(gòu)建鄰域粗糙集的特定類約簡。從經(jīng)典條件熵推廣后的鄰域近似條件熵出發(fā),分解提取關(guān)于特定類的鄰域近似條件熵,證明信息粒化非單調(diào)性,建立特定類約簡及其啟發(fā)算法,并提供實(shí)例分析與實(shí)驗(yàn)驗(yàn)證。
2 鄰域粗糙集及高層鄰域近似條件熵
決策表NDT=<U,C,D >包括有限論域U、條件屬性集C={c1,c2,…,cl}、決策屬性集D。鄰域體系涉及距離函數(shù)d與半徑參數(shù)δ。本文采用Manhattan 距離可得鄰域nC(x)={y∈U|dC(x,y)≤δ}、鄰域關(guān)系NC={(x,y)∈U×U|dC(x,y)≤δ}、鄰域覆蓋U/NC={nC(x)|x∈U} 。任意條件屬性子集B?C可以產(chǎn)生相關(guān)概念,如鄰域采用nB(x)或(x)并設(shè)鄰域粒數(shù)為n。設(shè)決策分類U/IND(D)={Dj|j=1,2,…,m}具有m個(gè)決策類。
定義1[7]決策類Dj關(guān)于B?C的鄰域上下近似為:

基于文獻(xiàn)[8-9,15-16],下面自然建立鄰域(近似)條件熵,其中鄰域及其粒數(shù)采用不重復(fù)規(guī)則,有利于覆蓋粒結(jié)構(gòu)推理;當(dāng)覆蓋退化到劃分時(shí),它們將退化到經(jīng)典粗糙集的(近似)條件熵。
定義2 決策屬性集D相對于B?C的鄰域條件熵為:

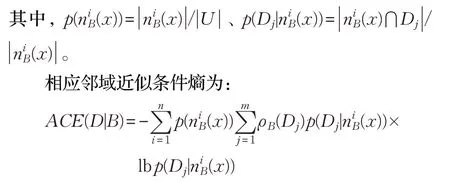
鄰域條件熵CE(D|B)采用經(jīng)典條件熵公式,將等價(jià)剖分結(jié)構(gòu)泛化推廣到鄰域覆蓋結(jié)構(gòu),具有相應(yīng)不確定性語義。鄰域近似條件熵ACE(D|B)引入鄰域近似粗糙度ρB(Dj)作為權(quán)重系數(shù),有效融合覆蓋結(jié)構(gòu)信息與近似逼近信息,變得更為強(qiáng)健。
3 中層鄰域近似條件熵
上述高層鄰域(近似)條件熵適用于整個(gè)決策分類。下面對它們施行“求和換序”與“分解提取”,得到中層相應(yīng)概念,以適用于特定決策類。
定義3 決策類Dj相對于B?C的鄰域條件熵為:

中層鄰域條件熵CE(Dj|B)對所有不重復(fù)鄰域粒實(shí)施信息集成,表征鄰域覆蓋結(jié)構(gòu)對于特定決策類的不確定性程度。基于信息融合[15-16],ACE(Dj|B)集成了信息度量CE(Dj|B)與結(jié)構(gòu)度量ρB(Dj)的不確定性信息,有效用于鄰域粗糙集的特定類約簡構(gòu)建。下面揭示CE(Dj|B)、ACE(Dj|B)的上下界與粒化非單調(diào)性。為此,提取定義3公式內(nèi)層,記

定理1(1)CE(Dj|B)∈[0,|Dj|lb|U|]、ACE(Dj|B)∈[0,|Dj|lb|U|] 。(2)若BndB(Dj)=?,則CE(Dj|B)=0 、ACE(Dj|B)=0 。(3)若U/NB={U} 且Dj={x}?U,則CE(Dj|B)=(1/|U|)lb|U|、ACE(Dj|B)=(1/|U|)lb|U|。
證明(1)對特定類Dj,若鄰域)滿足)?Dj=?則p(Dj|))=0、CE(Dj|))=0。下面考慮交Dj的鄰域并,設(shè)Sj={i∈{1,2,…,n}x)?Dj≠?}則|Sj|≤n≤N(這里N=|U|)。 ?i∈Sj有p(Dj|))∈[1/N,1]與lbp(Dj|))≥lb 1/N。因此:

(2)若BndB(Dj)=?,這意味著?nB(x)∈U/NB,nB(x)?Dj=?、p(Dj|nB(x))=0 或nB(x)?Dj=nB(x) 、p(Dj|nB(x))=1,即CE(Dj|nB(x))=0。從而CE(Dj|B)=0;進(jìn)而ACE(Dj|B)=0,其中ρB(Dj)=0。
(3)若U/NB={U} 且Dj={x}?U,即只存在唯一鄰域U,且其滿足p(Dj|U)∈(0,1)、lbp(Dj|U)=lb(1/N),根據(jù)公式(1)有CE(Dj|B)=(|Dj|/|U|)lb|U|=(1/|U|)lb|U|。進(jìn)而ACE(Dj|B)=(1/|U|)lb|U|,其中ρB(Dj)=1。
定理2 設(shè)屬性子集A,B?C誘導(dǎo)的鄰域覆蓋U/NA、U/NB具有粒化關(guān)系U/NA-?U/NB(即?x∈U有nA(x)?nB(x)),則CE(Dj|A)與CE(Dj|B)、ACE(Dj|A)與ACE(Dj|B)無必然大小關(guān)系。
證明因?yàn)閁/NA-?U/NB有nA(x)?nB(x) 。該嵌套鄰域結(jié)構(gòu)與決策類Dj具有三種相交情況。
(1)若nA(x)?Dj=nB(x)?Dj=即p(Dj|nA(x))=p(Dj|nB(x))=0,則可以得到:

(2)若?=nA(x)?Dj?nB(x)?Dj則0=p(Dj|nA(x))≤p(Dj|nB(x))≤1。由于上凸函數(shù)-plbp的非單調(diào)性,不能確定p(Dj|nA(x))×lbp(Dj|nA(x))與p(Dj|nB(x))×lbp(Dj|nB(x))的大小關(guān)系。從而,也不能確定CE(Dj|nA(x))與CE(Dj|nB(x))大小關(guān)系。
(3)若??nA(x)?Dj?nB(x)?Dj,但兩個(gè)非0 概率p(Dj|nA(x))與p(Dj|nB(x))之間的大小不確定[18],故CE(Dj|nA(x))與CE(Dj|nB(x))大小關(guān)系也是不確定的。
綜上,CE(Dj|nA(x))與CE(Dj|nB(x))無必然大小關(guān)系。后續(xù)粒化結(jié)構(gòu)的重復(fù)計(jì)數(shù)消除過程也具有不確定性,故基于U/NA與U/NB結(jié)的CE(Dj|A)與CE(Dj|B)無必然大小關(guān)系。進(jìn)而,ACE(Dj|A)與ACE(Dj|B)也無必然大小關(guān)系。
4 基于鄰域近似條件熵的特定類屬性約簡
基于中層鄰域(近似)條件熵及其不確定性語義、粒化非單調(diào)性,本章構(gòu)建相應(yīng)的特定類屬性約簡及其啟發(fā)算法,主要采用具有信息修正的鄰域近似條件熵。
定義4 基于鄰域近似條件熵,B?C稱為C相對于決策類Dj的一個(gè)約簡,若如下兩條成立:

這里的約簡目標(biāo)追求更大的鄰域近似條件熵值,這種單向方案已經(jīng)實(shí)際使用[18]。定義中的兩條分別對應(yīng)“聯(lián)合充分性”與“個(gè)體必要性”。接下來,類似于文獻(xiàn)[18],引入屬性重要度并構(gòu)建啟發(fā)式約簡算法。
定義5a∈B關(guān)于B的內(nèi)屬性重要度為:

內(nèi)重要度sigin(a,B,Dj)表示在B中刪除屬性a產(chǎn)生的關(guān)于鄰域近似條件熵的信息減量,而外重要度sigout(a,B,Dj)表示在B上增加屬性a產(chǎn)生的信息增量,兩者提供了快速約簡的屬性選擇機(jī)制。若a關(guān)于B是重要的,那么鄰域近似條件熵滿足關(guān)系A(chǔ)CE(Dj|B)>ACE(Dj|B-{a}), 因此sigin(a,B,Dj)>0, 反之sigin(a,B,Dj)<0 ;對于a∈(C-B) ,若a關(guān)于B是重要的,則ACE(Dj|B?{a})>ACE(Dj|B),因此有sigout(a,B,Dj)>0,反之sigout(a,B,Dj)≤0。由此,下面采用這兩種重要度來設(shè)計(jì)一個(gè)啟發(fā)式搜索算法,以快速得到一個(gè)特定類約簡。
算法1 基于鄰域近似條件熵的特定類屬性約簡啟發(fā)算法。
輸入 決策表NDT=<U,C,D >,鄰域半徑δ;
輸出 基于鄰域近似條件熵的特定類約簡R。
步驟1 設(shè)置R=。
步驟2 計(jì)算?a∈C的內(nèi)屬性重要度sigin(a,C,Dj),滿足sigin(a,C,Dj)>0 的屬性a均加入R(即實(shí)施循環(huán)更新R←R?{a})。
步驟3 計(jì)算子集R與全集C關(guān)于特定類Dj的鄰域近似條件熵ACE(Dj|R)與ACE(Dj|C)。若ACE(Dj|R)≥ACE(Dj|C),則進(jìn)入步驟5,否則進(jìn)入步驟4。
步驟4 計(jì)算?a∈(C-R)的外屬性重要度sigout(a,R,Dj),并選擇屬性重要度最大的屬性a*并入R(即施行一次更新R←R?{a*}),并進(jìn)入步驟3。
步驟5 ?a∈R,若屬性a滿足ACE(Dj|R-{a})≥ACE(Dj|R),則從R中刪除a(即采用循環(huán)更新R←R-{a})。
步驟6 返回R。
算法1 優(yōu)化了文獻(xiàn)[18]的非單調(diào)性算法結(jié)構(gòu),并主要采用鄰域近似條件熵。步驟1是初始化。步驟2是啟發(fā)搜索過程,主要在條件屬性全集C中選取對類Dj具有相關(guān)模式識(shí)別功能的屬性。步驟3是一個(gè)評(píng)估過程,若步驟2 得到的子集R的鄰域近似條件熵小于全集C的(即ACE(Dj|R)<ACE(Dj|C)),則需要利用步驟4 進(jìn)行剩余屬性的啟發(fā)式搜索,并加入最優(yōu)屬性以快速完成添加。可見,鄰近步驟5 的R必然滿足約簡“聯(lián)合充分性”,但不一定滿足約簡“個(gè)體必要性”。由此,步驟5采用反向冗余刪除,最終獲得約簡“個(gè)體必要性”。基于文獻(xiàn)[18]的算法分析過程與結(jié)果,這里的算法1 計(jì)算量仍舊主要集中在步驟2,因此整個(gè)的時(shí)間復(fù)雜度為O(|C||U|lb |U|)。該算法是有效的,能夠得到一個(gè)基于鄰域近似條件熵的特定類屬性約簡。
5 決策表實(shí)例
本章提供一個(gè)實(shí)例,說明度量性質(zhì)與屬性約簡。決策表NDT=<U,C,D >如表1,其包括兩個(gè)決策類:D1={x1,x2}、D2={x3,x4}。

表1 實(shí)例決策表
基于Manhattan 距離與鄰域半徑δ=0.4,下面聚焦屬性增鏈

該鏈誘導(dǎo)出鄰域覆蓋及其粒化關(guān)系:

由此,可得兩個(gè)特定類的鄰域粗糙度:

上述所有值均隸屬理論雙界范圍[0,|Dj|lb |U|=4](定理1)。4個(gè)不等式驗(yàn)證了粒化非單調(diào)性(定理2)。
最后分析特定類約簡,主要采用決策類D2來說明算法1。步驟1 賦值R=?。步驟2 計(jì)算3 個(gè)條件屬性的內(nèi)重要度:

由此沒有屬性滿足加入條件sigin>0,故R=?。此時(shí)R達(dá)不到約簡第一條,在步驟3 中判斷后需要轉(zhuǎn)入步驟4,計(jì)算3個(gè)條件屬性的外重要度:

基于最大值隨機(jī)選取一個(gè)屬性如c1并入R,有R={c1}。此時(shí),用更新的R={c1}進(jìn)入步驟3,檢驗(yàn)有:

即{c1} 滿足約簡第一條從而進(jìn)入步驟5。基于步驟5,單屬性c1不能被刪除,即{c1} 滿足約簡條件第二條,并最終在步驟6中輸出作為約簡結(jié)果。
6 UCI數(shù)據(jù)實(shí)驗(yàn)
本章實(shí)施數(shù)據(jù)實(shí)驗(yàn)來驗(yàn)證鄰域(近似)條件熵及其特定類約簡,主要是粒化非單調(diào)性(定理2)與啟發(fā)式約簡算法(算法1)。下面從UCI 機(jī)器學(xué)習(xí)知識(shí)庫(http://archive.ics.uci.edu/ml)中選取5 組數(shù)據(jù)集,如表2。首先采用最大-最小標(biāo)準(zhǔn)化數(shù)據(jù)預(yù)處理,仍用Manhattan距離函數(shù),鄰域半徑參見表2。
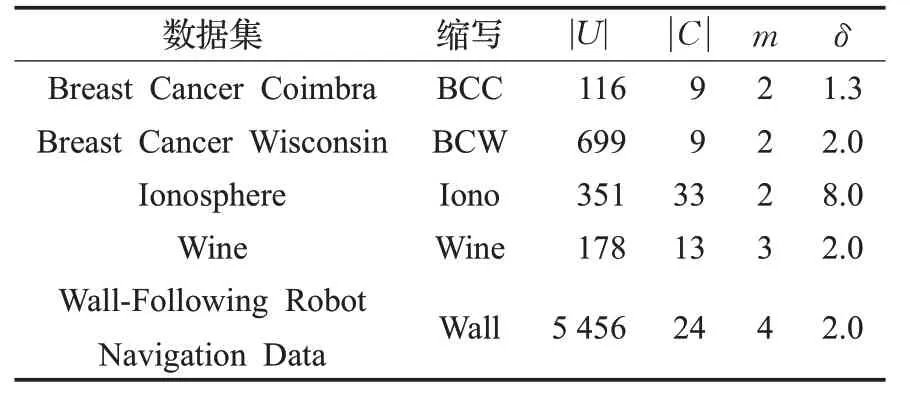
表2 5類UCI數(shù)據(jù)集的基本描述
為表現(xiàn)度量變化,特選取自然屬性增鏈{c1}?{c1,c2}?…?C。針對所有的13 個(gè)決策類,進(jìn)行了完全實(shí)驗(yàn)計(jì)算;這里提供代表呈現(xiàn),對此前3 個(gè)數(shù)據(jù)選取D2而后2 個(gè)數(shù)據(jù)集選取D1,相關(guān)度量結(jié)果參見圖1。在圖1 中,橫坐標(biāo)整數(shù)標(biāo)識(shí)屬性增鏈元B,縱坐標(biāo)實(shí)數(shù)標(biāo)識(shí)鄰域條件熵CE(Dj|B)、鄰域近似精度αB(Dj)(即1-ρB(Dj))、鄰域近似條件熵ACE(Dj|B)。觀測可見,αB(Dj)很接近于0,CE(Dj|B)與ACE(Dj|B)具有細(xì)微調(diào)整差距,它們的粒化非單調(diào)性非常明顯。基于這些非單調(diào)變化曲線,追求鄰域近似條件熵大值的特定類約簡是合理的,其可以得到適當(dāng)長度的約簡結(jié)果。

圖1 5類UCI數(shù)據(jù)集關(guān)于屬性增鏈的三種度量變化
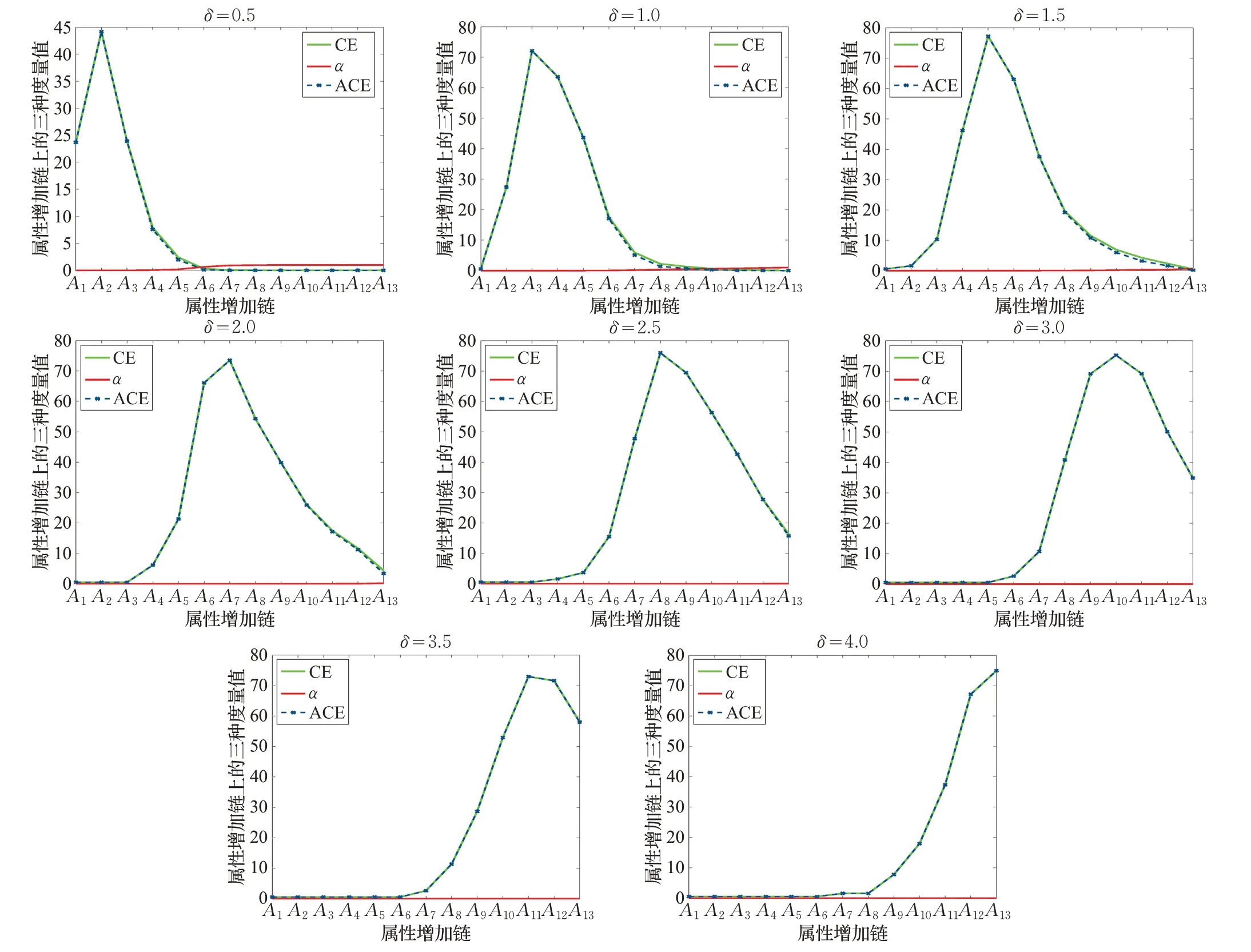
圖2 Wine數(shù)據(jù)集D1 類關(guān)于屬性增鏈與半徑增鏈的三種度量變化
最后分析鄰域半徑對度量與約簡的結(jié)果影響。作為代表,選取數(shù)據(jù)集Wine 的D1類,以δ=0.5 為初始值并以0.5 為步長構(gòu)造半徑增鏈。圖2 提供了CE(Dj|B)、αB(Dj)、ACE(Dj|B)在半徑增鏈與屬性增鏈上的變化。基于圖2,對于鄰域近似條件熵,通常的半徑能夠較好表現(xiàn)粒化非單調(diào)性,而波峰或最大值隨著半徑增大而右移;可見,半徑取值決定著度量數(shù)值以及后續(xù)約簡。
進(jìn)而,表3提供了特定類約簡結(jié)果,驗(yàn)證了算法1的有效性。表4 則提供了Wine 數(shù)據(jù)集D1類相關(guān)半徑增鏈的約簡結(jié)果。基于表4,約簡具有隨半徑變大而屬性增多的大體趨勢;鄰域半徑過小(如0.5)會(huì)導(dǎo)致屬性約簡太單一,半徑過大(如4.0)則約簡太冗余,即這兩種極端情況下的約簡結(jié)果都不太理想;當(dāng)δ取2.0、2.5、3.0時(shí),約簡結(jié)果較好。此外,其他數(shù)據(jù)集實(shí)驗(yàn)都表現(xiàn)出類似結(jié)果,即適中的鄰域半徑能夠有效表現(xiàn)粒化非單調(diào)性并獲取較好屬性約簡,而表2中的半徑取值正是經(jīng)過實(shí)驗(yàn)分析所得的較好參數(shù)設(shè)置。

表3 5類UCI數(shù)據(jù)集的特定類約簡

表4 Wine數(shù)據(jù)集D1 類關(guān)于半徑增鏈的約簡
7 結(jié)束語
本文粒化分解決策表高層的鄰域(近似)條件熵,提取出中層的鄰域(近似)條件熵,獲得信息上下界與粒化非單調(diào)性,進(jìn)而構(gòu)建特定類屬性約簡及其啟發(fā)式約簡算法。本文構(gòu)建鄰域(近似)條件熵深化了文獻(xiàn)[15-16]的相關(guān)度量,后續(xù)特定類屬性約簡推廣了文獻(xiàn)[2]的經(jīng)典特定類約簡,而相關(guān)啟發(fā)式約簡算法模擬并優(yōu)化了文獻(xiàn)[18]的算法。所得結(jié)果有利于特定類模式識(shí)別的不確定性度量與優(yōu)化應(yīng)用,值得深入探討。

