水聲環境UWA信道散射模型參數仿真分析

周文軒，周 杰，2，劉少云，英 文

1.南京信息工程大學 電子與信息工程學院，南京210044

2.日本國立新瀉大學 工學部 電氣電子工學科，新瀉950-2181

1 引言

水聲（Underwater Acoustic，UWA）通信系統在20世紀主要被應用于軍事領域[1]，而目前UWA通信技術在海洋信息數據采集、環境監測[2]、沿海石油勘探以及水下機器人控制等諸多領域發揮著重要作用。然而，由于激光和電磁波水下傳播具有高損耗率，因而一般采用聲波來傳遞信息。根據射線理論，假設聲波在水中的傳播方式與光線的能量相似，沿著直線傳播，聲波傳播速度為一常量。在UWA通信系統中，Rx處的接收信號可以通過多徑分量（Multipath Components，MPC）的總和來建模，其中每個MPC 以不同的時間延遲從不同的方向到達。由于UWA 信道是一種復雜的時空頻變信道[3]，每個MPC都有獨特的時空差異，這不僅直接影響信道特性，還影響接收機的決策。例如，由接收端Rx 的移動性引起的多普勒效應取決于AOA。類似地，在寬帶UWA通信系統中，TOA 的分布在整個系統的時延分析中起著至關重要的作用。因此，缺乏TOA、AOA 和AOD 的統計數據會導致UWA 信道模型的不準確，與實際系統性能研究的目標相矛盾。

TOA、AOA 和AOD 的統計數據主要取決于兩個因素。一個是傳播區域的幾何形狀;另一個是傳播區域內局部散射體的分布。設計合適的UWA 通信系統，信道模型不可或缺。已有研究人員針對UWA通信系統提出了建立幾何散射模型的假設。幾何假設包括Tx、Rx 的位置以及散射區域的形狀。其中，典型的散射區域主要由環形、圓盤和橢圓形建模。在文獻[4-5]中，研究了一種環形模型，其中局部散射體分布在以Rx 為中心的薄環上。文獻[6]對空心圓盤模型的TOA 和AOA 的統計數據進行了研究，其中散射體位于空心圓盤內。在文獻[7-8]中提出了另一種幾何模型，其中散射體分布在以Rx 為中心的整個圓盤內。文獻[8-10]研究了橢圓模型中的散射體情況。最后，在文獻[11]中引入了豎直矩形散射區域，并對其信道的各項理論參數進行了分析。

另一方面，需要考慮所選水底幾何模型內局部散射體的分布。由于均勻分布的簡單性，以前的大多數研究都假設局部散射體均勻分布在散射區域[6，8，11-12]。然而，對于更現實的情況，局部散射體通常以高斯分布的方式分布在以Rx 為中心的圓盤中，在文獻[12-14]中可以找到TOA和AOA統計的一些研究。然而，由于高斯分布的復雜性，所獲得的結果主要以積分表達式或近似解的形式呈現。

考慮到上述兩個關鍵因素，本文對基于水底幾何圓盤UWA 信道散射模型的TOA、AOA 和AOD 統計數據進行了研究，其中局部散射體隨機分布在以Rx 為中心的圓盤上。所提出的圓盤UWA信道模型的新穎性在于假設散射體均勻分布在極坐標中而不是在笛卡爾坐標中。根據所提出圓盤模型，其中局部散射體在極坐標中聯合均勻分布，可以觀察到圓盤中心周圍的散射體密度較高，而遠離中心點的散射體密度較低。事實上，通過在極坐標中采用聯合均勻分布，可以避免高斯PDF所帶來的高度數學復雜性，但卻沒有忽略文獻[14]中強調的高斯分布的有利特性。此外，假設從Tx發射的UWA波經過圓盤內部的局部散射體發生單次反射之后到達Rx。基于上述因素，本文推導了圓盤UWA信道散射模型的傳播統計特征，并解決了此前文獻中關于類似模型由于高斯復雜性而僅僅獲得積分形式解或近似解的情況，取得了更簡單但精確的表達式。

2 系統模型

水底幾何圓盤UWA信道散射模型如圖1所示。假設Tx 與Rx 位于同一二維（2D）水底平面環境上，其中Tx處于非散射區域，旨在將UWA波發送到處于富散射區域的Rx。假設Tx和Rx之間的距離為L,θT、θR分別表示AOD和AOA。此外，假設局部散射體隨機且獨立地分布在以Rx 為中心，以R為半徑的圓盤內，且距離Rx越遠越稀疏。每個散射體的位置可以用極坐標(r,θR)表示，其中r表示散射體與Rx 的距離。假設圓盤內的每個散射體均全向散射，其反射系數都相同且散射體間互不影響。由于具有較高的路徑損耗，因此忽略了來自圓盤以外散射體的影響，并假設從Tx發射的UWA波經過位于圓盤內隨機分布的散射體單次反射之后到達Rx。最后，假設Tx 和Rx 都配備了全向天線，這樣在計算UWA 波的空時信道參數時，就可以避免由于天線方向圖變化而導致的散射體區域的變化。

圖1 水底單反射幾何圓盤UWA信道散射模型

如上所述，假設局部散射體隨機且獨立地分布在以Rx 為中心，以為R半徑的圓盤內。該隨機性通過聯合均勻PDF建模，并可以用以下極坐標表示：

由上所述，公式（1）中的聯合均勻PDF 也可以用以下笛卡爾坐標表示：

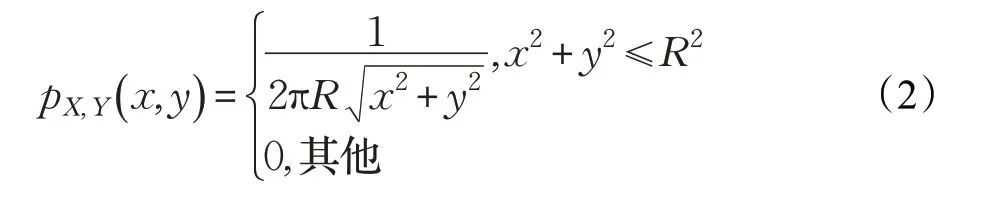
需要注意的是，公式（2）與下面公式（3）的笛卡爾坐標中的均勻分布完全不同：

其中假設局部散射體在圓盤內均勻分布，由此給出的水底圓盤UWA信道散射模型可由以下極坐標表示：

在文獻[6，8，12]中，由公式（3）或（4）描述的圓盤散射模型的統計特征已被廣泛研究。然而，本文旨在分析水底環境的UWA 信道，且通過極坐標中的聯合均勻PDF來描述局部散射體的分布，其已在公式（1）和（2）中給出。圖2 給出了本文所提出的隨機分布的局部散射體，其中半徑R=50 m 其通過使用公式（1）中的PDF 生成。可以在原點附近即Rx位置處觀察到更高密度的局部散射體，且散射體的密度隨著與Rx 的距離也即r值的增加而減小，這更接近作為高斯分布的局部散射體的物理現實。這一現象得到以下事實的支持：在許多海底環境中，由海底植物和沙石等構成的局部散射體在Rx周圍具有高密度，在較遠距離處具有較低密度，或者也可以理解為近端散射體作用大于遠端散射體。通過在極坐標系中建立如公式（1）所示的聯合均勻分布PDF，對比在笛卡爾坐標系中建立如公式（3）所示的聯合PDF，或是在文獻[13-15]中研究過的聯合高斯PDF，可以在生成的隨機UWA 信道模型的統計特征方面，顯著地降低問題的復雜度。因為若采用笛卡爾坐標系對散射體建模，則散射體位置需要以坐標( )x,y表示，對比在極坐標系只需中引入一個變量r，在后續的統計特征推導過程中，會增加額外的計算復雜度。

圖2 水底圓盤內局部散射體分布圖

3 水底圓盤UWA信道模型的統計特性

根據上述的水底UWA 信道參考模型，本章推導出其TOA 和AOA 的 聯 合PDF 以 及AOD 和AOA 的 聯 合PDF 的閉式表達式。此外，還計算了其TOA、AOA 和AOD的邊緣PDF。

3.1 TOA和AOA的聯合PDF

通過參考圖1 的UWA 信道模型，并且只考慮單次反射，UWA 波經過散射體從Tx 傳播到Rx 的總路徑長度為：

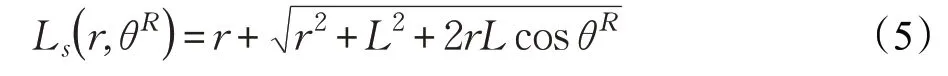
為了得到TOA 和AOA 的聯合PDF，引入函數τ'(r,θR)=Ls(r,θR)/cs及輔助函數S(r,θR)=θR[15]，其中τ'表示TOA，cs=1 500 m/s（等速環境）表示聲波在海水中的傳播速度[1]。可以看出，這些函數的根可由下式給出：

通過應用隨機變量轉換的概念[16]，TOA 和AOA 的聯合PDF可以表示為：

將此表達式代入到公式（7）的聯合均勻PDF 中，可以得出TOA和AOA的聯合PDF，表示如下：

其中，[],θR∈[-π,π] 。符號和分別表示最小和最大TOA。根據圖1，當散射體與Rx 具有最小距離時，TOA 為,即當r→0,則。類似地，當散射體與Tx相距最大距離時，即當r→R且θR→0 時(L+2R)，取得最大TOA為。

3.2 AOD和AOA的聯合PDF

采用圖1中的幾何圓盤UWA信道散射模型并根據正弦定律，θT可以表示為：

通過再次使用隨機變量轉換的概念，可以得到以下AOD和AOA聯合PDF的表達式：

注意到 |J|-1可以很容易地被簡化為| ?r/?θT|的形式，通過結合公式（1）中的聯合均勻PDF，θT和θR的聯合PDFpθT,θR(θT,θR)可以用以下的閉式表示：

3.3 TOA的邊緣PDF

根據公式（9）中的聯合PDFpτ',θR(τ',θR)，并對AOAθR進行積分，可以得到TOAτ'的邊緣PDFpτ'(τ')，表示如下：

其中，DθR是在給定TOA情況下AOAθR的變化域。由于，并根據公式（5），可得：

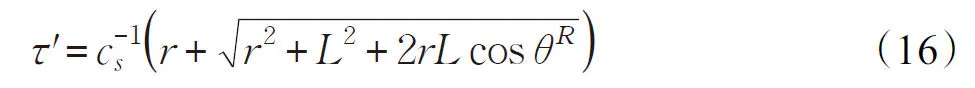
顯然，公式（16）是關于r的單調遞增函數。這意味著對于給定的AOAθR的值，如果散射體位于圓盤模型的圓周上，則TOAτ'取得其最大值，用τ'R(θR) 表示，即：

實際上，對于給定的TOAτ'，和之間的區間給定了AOAθR的變化域DθR。該變化域也確定了公式（15）中的積分限制。

現在，通過公式（18）中給出的積分極限來求解公式（15）中給出的積分之后，TOAτ'的PDFpτ'( )τ'可以通過以下閉式表示：

3.4 AOA的邊緣PDF

根據公式（9）中的聯合PDFpτ',φR()，并對TOAτ'進行積分，得到AOAθR的邊緣PDFpθR(θR)表示如下：

其中，Dτ'是在給定AOAθR情況下TOAτ'的變化域。對于給定的AOAθR的值，由公式（17）看出，TOAτ'從其最小值τ'min變化到τ'R( )θR。因此，通過求解公式（21）中的積分并考慮變化域Dτ'，可以得出均勻分布的AOAθR的PDFpθR(θR)，表示如下：

事實上，也可以直觀地期望由于Rx 周圍的局部散射體的圓對稱分布，AOA應該在水底圓盤UWA信道散射模型中均勻地分布。

此外，為了得到邊緣PDFpθR(θR)，可以對公式（1）中的pr,θR(r,θR)的半徑r進行積分。這樣可以直接得到公式（22）中的結果。

3.5 AOD的邊緣PDF

AODθT的邊緣PDFpθT(θT)可以通過對公式（13）給出的聯合PDFpθT,θR(θT,θR)中的AOAθR進行積分得到。AODθT的邊緣PD) 表示如下：

其中，為了上述使表達式簡單且僅與θT有關而引入的輔助函數G(θT)的表達式如下：

對于給定的AODθT值，DθR是AOAθR的變化域，通過求解公式（10）中的θR，可以方便地求出該變化域。此外，由于公式（10）中的θT(r,θR)是關于r的單調遞增函數，可以將r設為其最大值R。根據上述過程，公式（24）中積分的極限范圍從arcsin(ηsinθT)+θT到π-arcsin(ηsinθT)+θT，這也就是變化范圍LθR。

3.6 平均時延

通過考慮3.3 節TOA 的PDF 先驗結果，可以推導出水底圓盤UWA 信道散射模型的平均時延及其時延擴展。

其中，平均時延由TOAτ'的第一時刻定義，即：

根據公式（19）中的pτ'(τ')，對于所提出的水底圓盤UWA信道散射模型的平均時延，不存在閉式解。因此，可以利用數值積分技術來顯示平均時延的特征。

3.7 時延擴展

由上述平均時延以及3.4 節的先驗結果，則時延擴展可由TOAτ'的第二中心矩的平方根定義，即：

表1 圓盤UWA信道參數定義及取值

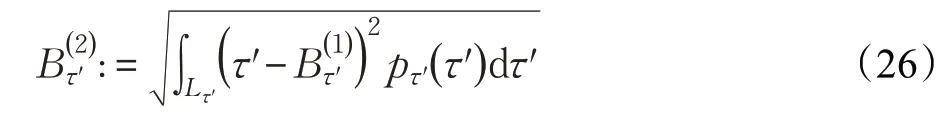
其次，根據公式（19）中的pτ'(τ')，對于所提出的圓盤UWA信道散射模型的時延擴展，不存在閉式的解。因此，再次利用數值積分技術來分析。

3.8 多普勒頻率PDF

通過使用在3.4節中求出的AOA的邊緣PDF，可以推導出多普勒頻率f的PDF。

在3.4 節中，通過兩種不同的方法證明了AOAθR遵循公式（22）中的均勻分布。在這種情況下，多普勒頻率f的PDFpf(f)可由Jakes分布給出[17]：

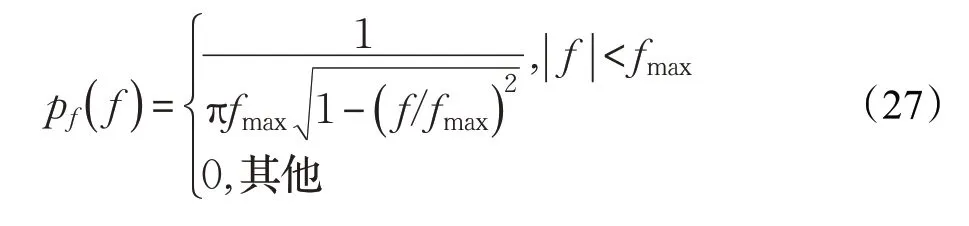
4 數值仿真結果與分析

本章是對前面所提出的統計特征的仿真分析。表1給出了該模型在水下傳輸場景中的信道參數定義及取值，若無特殊說明，則默認為表中的取值。

圖3 是根據公式（9），由MATLAB 軟件仿真得到參考模型UWA 信號的TOAτ'和AOAθR的聯合PDF 圖。可以看出，時延基本都分布在較短時間內。此外，還可發現當TOAτ'最小且AOAθR=±π 時，pτ',θR(τ',θR)取得最大值，這是因為UWA沿著視距直達（Line of Sight，LoS）方向從Tx 傳播到Rx，且距離圓盤中心越近，散射體密度越大，這與預期結果相符合。

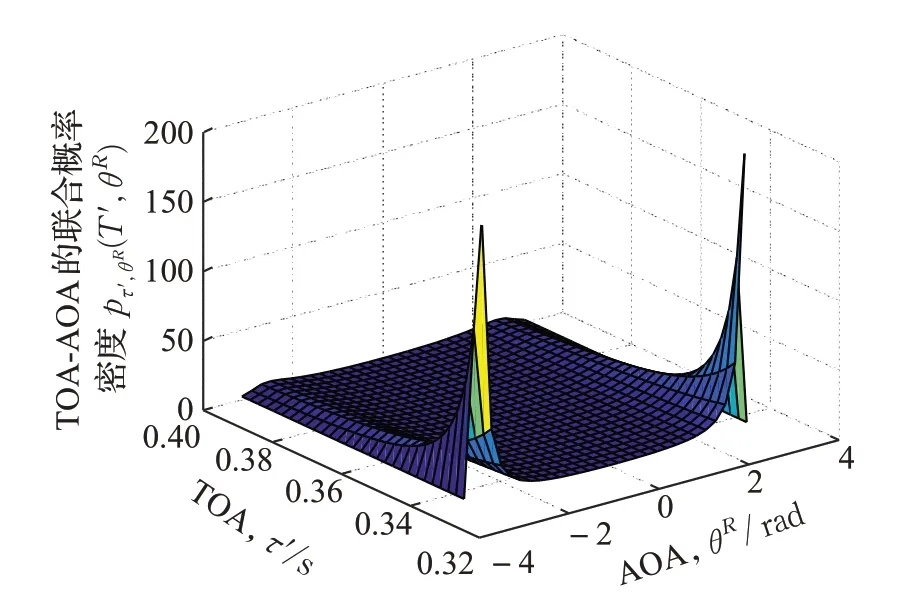
圖3 水底圓盤UWA信道模型TOA τ'和AOA θR的聯合PDF pτ',θR(τ',θR)

圖4 根據公式（13）仿真得到，它給出了θT和的θR的聯合PDF圖。由圖4可知，pθT,θR(θT,θR)在θT=0 且θR也處于零值附近時取得最大值。此外，只有在θT?θR≥0時，pθT,θR(θT,θR)才大于零。這是顯而易見的，因為通過選擇θT和θR的值使得θT?θR＜0 時，則不可能在如圖1所示的區域中找到散射體。

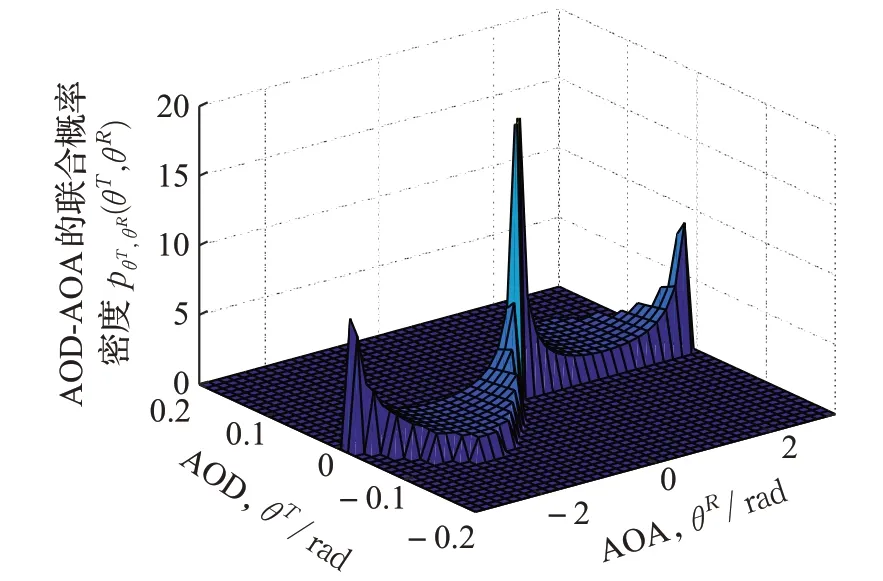
圖4 水底圓盤UWA信道模型AOD θT 和AOA θR的聯合PDF pθT,θR(θT,θR)

圖5 水底圓盤UWA信道模型的最大TOA τ'R(θR)與AOA θR 的關系

圖6給出了TOAτ'在不同的圓盤半徑R下對應的邊緣PDFpτ'(τ')，其中假設Tx與Rx的距離L依然設為500 m，圓盤半徑R分別取25 m、50 m和75 m。可以看出，在給定L值時，圓盤半徑R越小，TOAτ'的邊緣PDF 越大。對于所有給定的圓盤半徑R，TOAτ'的邊緣PDFpτ'(τ')在最小傳播時延τ'min附近具有高密度，在最大傳播時延τ'max( )L+2R附近具有低密度[6]，這符合期望。此外，從圖6 可以看出，TOAτ'遵循指數式分布，此分布通常被用在特定的信道模型中[18]，許多測量結果也證實了傳播時延的負指數特征[19]。然而，從文獻[6]中的圖5可以看出，通過使用公式（3）中的聯合PDF，TOA 的PDF 不能很好地遵循負指數函數。由此可知，通過極坐標中的聯合均勻PDF對局部散射體的分布建模比笛卡爾坐標中的聯合均勻PDF更好。

圖6 水底圓盤UWA信道模型TOA τ'的邊緣PDF pτ'(τ')

圖7 給出了不同的η=L/R對應的AODθT的邊緣PDF)。可以看出，在原點即θT=0處取得高密度的AOD，而在靠近散射體圓盤的圓周處，即arcsinη-1時取得較低值。考慮到笛卡爾坐標系中局部散射體的非均勻分布，圖7所示的數值結果達到了預期結果。此外，還可以觀察到AODθT分布在-0.2 rad 到0.2 rad 之間，這是因為在該圓盤模型中，圓盤的半徑R以及Tx與Rx之間的距離L是影響AODθT范圍的唯一因素，這一獨立性仿真結果也與預期結果相符合。

圖7 水底圓盤UWA信道模型AOD θT 的邊緣PDF pθT(θT)

圖8 給出了水底圓盤UWA 信道模型中，對于不同的從Tx 到Rx 的距離L與散射區域的半徑R對應的平均時延。可以看出，平均時延隨著R和L值的增加而增加。此外，在圖8中，通過將從Tx到Rx距離L從400 m增加到500 m然后增加到600 m，平均時延增加恒定的偏移，這是因為距離L增加的從Tx到Rx的傳播時延恒定。

圖8 圓盤半徑R 對應的平均時延

圖9 給出了對于不同的從Tx 到Rx 距離L，散射區域的半徑R對應的平均時延。可以看出，隨著R和L值的增加而增加。需要注意的是，正如圖9中標記的三角形所示，受R值的影響比L更大。這一現象是由于R增加25 m與L增加100 m對該模型的影響相同，導致在這兩種情況下都增加了0.07 s。

圖9 圓盤半徑R 對應的延遲擴展

5 結論

本文研究了水下環境中水底平面上幾何圓盤UWA信道散射模型中的TOA、AOA和AOD的統計特征。假設水底局部散射體隨機分布在以Rx 為中心的圓盤中。本文新穎性在于為了表示局部散射體的分布，本文提出了極坐標中的聯合均勻PDF，局部散射體以靠近Rx 的散射體密度更高，遠離Rx的密度更低的方式分布，更符合實際的海底散射環境，且簡化了計算過程。推導了TOA和AOA以及AOD和AOA的聯合PDF的閉式表達式。然后，計算了TOA、AOA 和AOD 的邊緣PDF。由仿真結果可知，TOA的PDF遵循負指數式函數分布，與文獻中的測量數據相符。此外，根據TOA的PDF，推導了水底幾何圓盤UWA信道散射模型的平均時延和時延擴展。數值結果表明，增加恒定的從Tx 到Rx 的距離，平均時延經歷恒定的偏移。此外，結果還表明，時延擴展受到Rx周圍的散射區域半徑的影響比從Tx到Rx距離的影響更大，這都符合預期結果。最后，證實了AOA遵循均勻PDF，這也表示多普勒頻率遵循Jakes 分布。本文的分析結論對水下聲通信環境的性能評估具有重要意義，拓寬了高效水聲信道的研究，為水聲通信設計提供了幫助。