孔隙式隔振系統非線性阻尼特性*

閆 明， 田浩男，劉海超

(沈陽工業大學 機械工程學院， 沈陽 110870)

為避免沖擊引起的破壞，艦載設備需要加裝隔振系統.采用大阻尼粘滯阻尼器的隔振系統可以顯著提高艦載設備的抗沖擊性能.粘滯阻尼器裝置結構簡單、耗能效果好，廣泛應用于航天、機械、軍事等領域的隔振系統中，尤其是雙出桿型液壓缸式粘滯阻尼器克服了單出桿型阻尼器因真空效應產生的拉壓力不均等弱點，可實現較大、較穩定的阻尼出力[1].

國內外學者對液壓孔隙式粘滯阻尼器進行了研究，de Domenico等研究了非線性流體粘滯阻尼器耗能結構的抗震性能，在優化設計過程中采用了一種新的等能量非高斯隨機線性化方法來處理非線性本構特性問題[2].van Tan等建立了某重型車輛的電子伺服閥液壓阻尼器模型，阻尼器模型參數由試驗數據確定[3].Singiresu提出在實際工程中按照基于周期內能耗守恒原則進行等效阻尼計算，使用等效阻尼系數和等效阻尼力替代液壓阻尼器實際產生的阻尼力，但需要利用試驗數據確定等效阻尼公式中的參數[4].孫靖雅等設計并制作了一種非牛頓流體粘滯阻尼器樣機，從流體力學角度分析阻尼力機理，建立了改進冪律模型，并通過擬合試驗數據獲得待定參數[5].王琳等利用AMESim軟件基于孔口流動原理建立了船用液壓阻尼器的數學模型，將通過仿真得到的液壓阻尼器速度響應曲線與試驗測得的速度響應曲線進行對比，證明了優化設計結果的有效性[6].

目前粘滯阻尼器的研究多集中于阻尼器減震性能分析、阻尼器結構參數優化和粘滯阻尼器力學模型建立等方向，由于粘滯阻尼器中的介質為非牛頓流體，因而阻尼力隨載荷形式和大小變化呈現非線性變化，粘滯阻尼器數學模型中的阻尼系數需要依據試驗數據來確定.試驗方法雖然能夠有效驗證理論結果，但增加了研究成本和周期.本文采用AMESim仿真軟件，針對孔隙式液壓阻尼器的阻尼力進行了理論和仿真研究，并通過試驗對仿真結果進行了驗證，為粘滯阻尼器非牛頓流體阻尼力的計算提供了有效、快捷的途徑.

1 液壓隔振系統數學模型

1.1 原理模型

艦船在行駛過程中的顛簸是一個隨機振動過程，為保證船載儀器設備的平穩性和安全性，需要安裝艦船用隔振系統.隔振系統原理模型如圖1所示，該系統主要包括彈性元件、阻尼元件和質量塊.為提高隔振效果，采用孔隙式液壓粘滯阻尼器，且該液壓粘滯阻尼器為速度相關型阻尼器[7].考慮到液壓油的壓縮性，液壓粘滯阻尼器產生的粘滯阻力具有非線性特征[8-10].在建立隔振系統原理模型時，將液壓粘滯阻尼器視為由彈簧和阻尼器構成的串聯結構[11-12].隔振系統參數如表1所示.

1.2 數學模型

為了研究隔振系統的隔振效果，需要建立隔振系統數學模型.以被隔離設備為研究對象，應用達朗貝爾原理建立隔振系統數學模型.以液壓粘滯阻尼器為研究對象，建立液壓粘滯阻尼器數學模型，相應模型表達式為

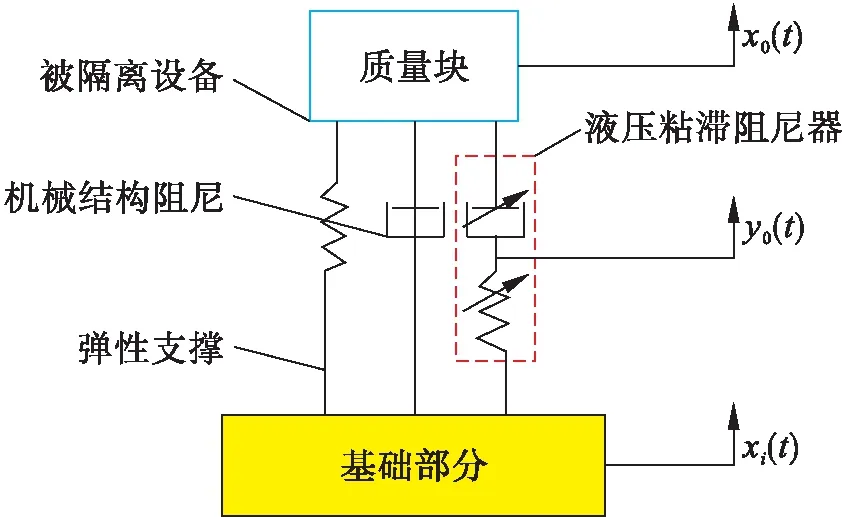
圖1 隔振系統原理模型Fig.1 Principle model for vibration isolation system

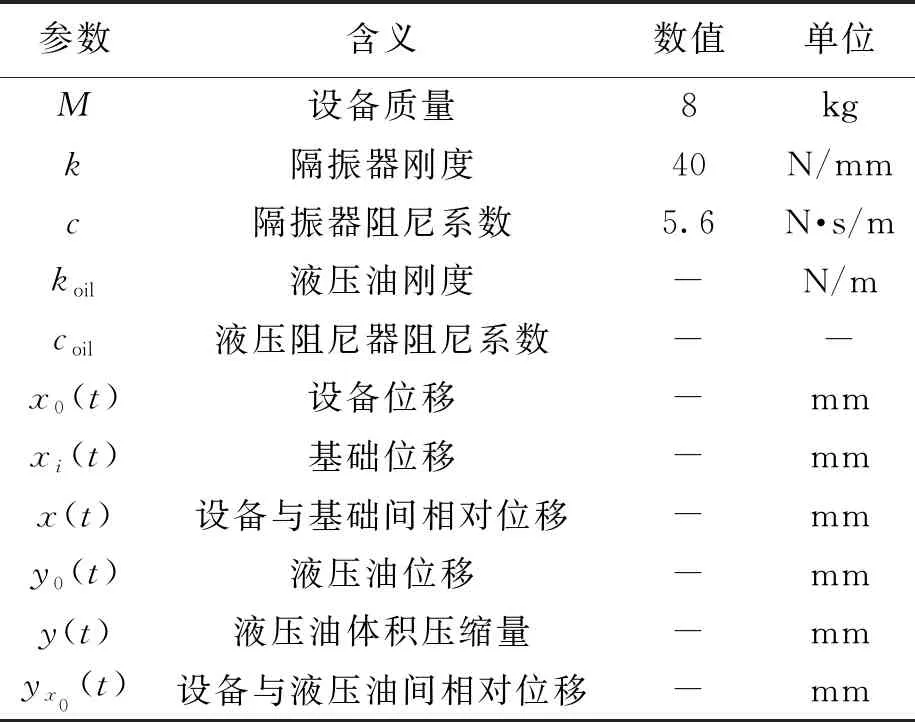
表1 隔振系統參數Tab.1 Parameters of vibration isolation system

(1)

(2)

由于y(t)是一個微小量，可以近似認為yx0(t)≈x(t)，修正后的隔振系統數學模型表達式為

(3)

隔振系統的輸入為沖擊載荷，根據德國軍標BV043-85的相關規定，采用圖2所示的正負雙半正弦波表示水下非接觸爆炸沖擊載荷，相應沖擊載荷參數如表2所示.

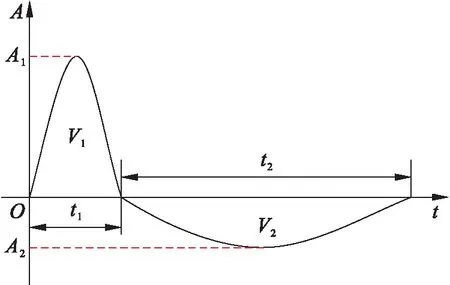
圖2 沖擊載荷Fig.2 Shock load

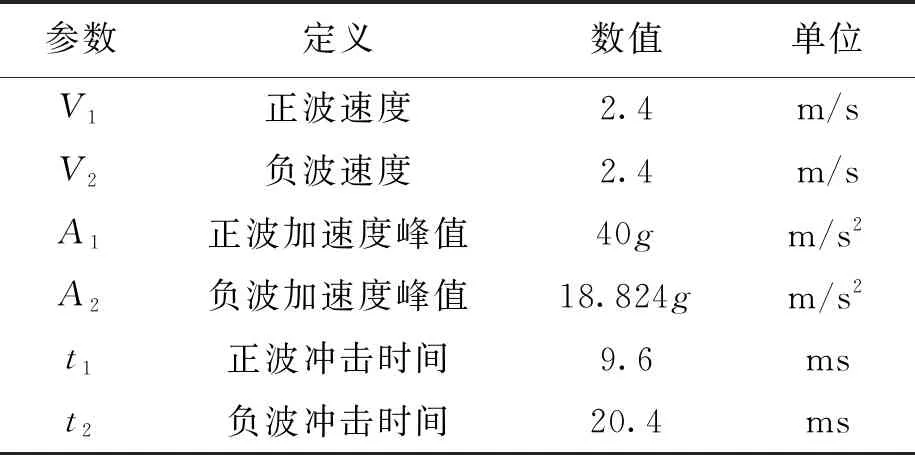
表2 沖擊載荷參數Tab.2 Parameters of shock load

加載函數表達式為

(4)

式中，f1、f2分別為正、負波頻率.

2 液壓阻尼力的分析與計算

在上述隔振系統中被隔離設備的質量、機械結構彈性元件的剛度和阻尼元件的阻尼都是已知參量，為了求解式(3)所示的隔振系統數學模型，必須求解液壓阻尼器的阻尼力.

2.1 理論計算

液壓阻尼力實際上由兩部分組成，分別為孔縮效應產生的阻尼力F1與粘滯摩擦阻尼力F2.設阻尼器活塞上開有S組孔徑不同的節流孔，且第i組節流孔直徑為d1i.設e為阻尼孔總面積，v為阻尼器相對運動速度，則液壓阻尼力表達式[13]為

coilv=F1+F2

(5)

(6)

式中：∑ζ為總阻力損失系數(選為0.49)，且∑ζ=ζc+ζe，ζc為入口收縮損失系數(選為0.15)，ζe為流速擴大損失系數(選為0.34)；ck為孔隙系數；α為孔縮衰減系數(0.1≤α≤2)，且α=0.103+(e/5)-0.175.

粘滯摩擦阻尼力表達式為

cNvm

(7)

式中：m為流動指數；cN為粘滯阻尼系數.非牛頓流體流動指數是一個小于1的量，由于m值的大小對cN影響不大，因而計算cN時可將m取為1.

液壓阻尼力表達式為

coilv=ckvα+cNvm

(8)

由于系統選用的油液為非牛頓流體，液壓油的流動指數是一個未知參量，因而無法通過理論計算確定粘滯摩擦阻尼力.本文利用AMEsim軟件[14]求解液壓阻尼力，確定阻尼力表達式中的流動指數，并完成數學模型的求解和試驗驗證.

2.2 仿真求解

雙出桿液壓孔隙式粘滯阻尼器的結構原理如圖3所示.該阻尼器主要由活塞桿、端蓋、帶節流孔的活塞和缸體幾部分組成，其主要參數如表3所示.雙出桿液壓孔隙式粘滯阻尼器的工作原理為：當粘滯阻尼器受到外部沖擊時，活塞與液壓缸缸體產生相對運動，迫使活塞一側油液通過節流孔流向另一側，由孔縮效應產生阻尼力來耗散沖擊能量，從而實現隔振的目的.

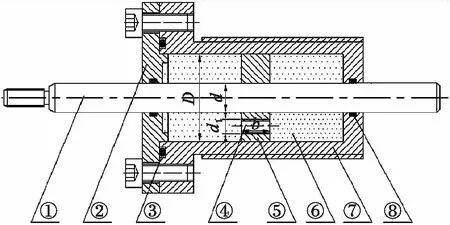
①活塞桿 ②端蓋 ③O型密封圈 ④節流孔 ⑤活塞 ⑥阻尼介質 ⑦缸體 ⑧型密封圈圖3 雙出桿液壓孔隙式粘滯阻尼器Fig.3 Double-out rod hydraulic pore-type viscous damper

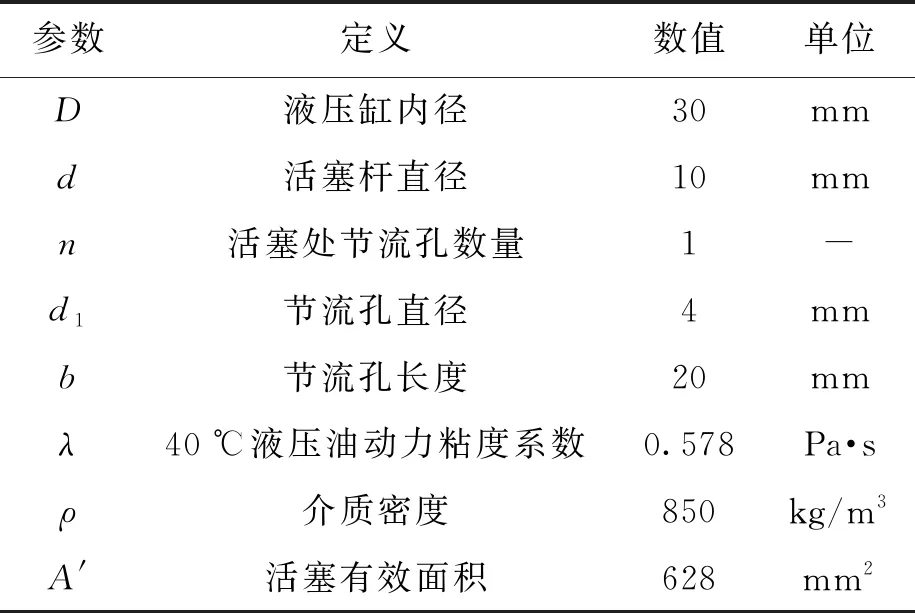
表3 液壓阻尼器參數Tab.3 Parameters of hydraulic damper

根據液壓隔振器的結構原理、流體力學特性和數學模型分析，分別建立液壓阻尼器、隔振彈簧和正負波輸入裝置的AMESim模型，結果如圖4所示.液壓限位隔離系統仿真計算模型主要包括信號源、隔離部分、液壓限位部分和質量塊四部分.

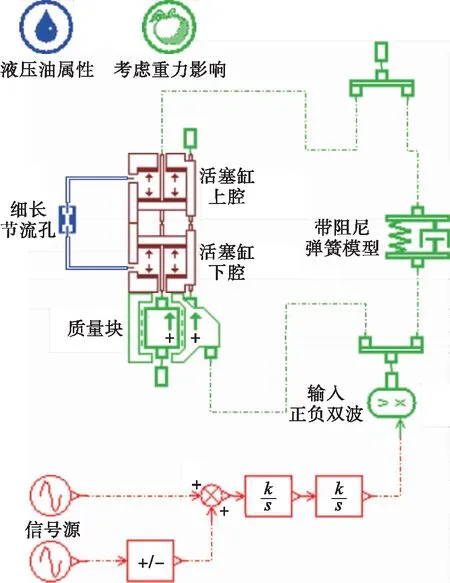
圖4 基于AMESim的液壓隔離系統仿真模型Fig.4 Simulation model for hydraulic vibration isolation system based on AMESim

在AMESim模型中施加式(4)所示的載荷，得到液壓缸上、下腔壓力，當輸入載荷(加速度峰值)A1為40g，A2為18.824g時，液壓缸上、下腔壓力如圖5所示.液壓缸上、下腔壓力差與活塞有效面積的乘積即為液壓阻尼器的阻尼力值[15]，即

ΔpA′=ckvα+cNvm

(9)

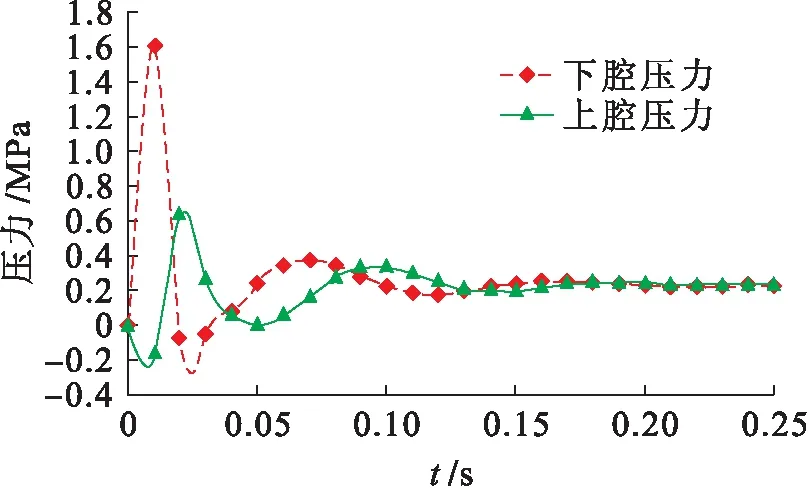
圖5 液壓缸上、下腔的壓力Fig.5 Pressure of upper and lower chambers of hydraulic cylinder

由式(9)求出流動指數，得到其平均值為0.838 6，將其代入式(8)中進行計算.將通過AMESim仿真得到的液壓阻尼器阻尼力ΔpA′與由式(8)計算得到的阻尼力coilv進行比較，結果如圖6所示.由圖6可見，阻尼力ΔpA′與coilv趨勢非常接近，最大峰值誤差為4.6%.

為了探究阻尼器結構參數對系統性能的影響，對阻尼孔尺寸與阻尼力的關系進行了仿真分析，將AMESim模型中阻尼孔的直徑分別設定為2、3、4、5和6 mm，施加同樣載荷得到圖7所示的阻尼力.

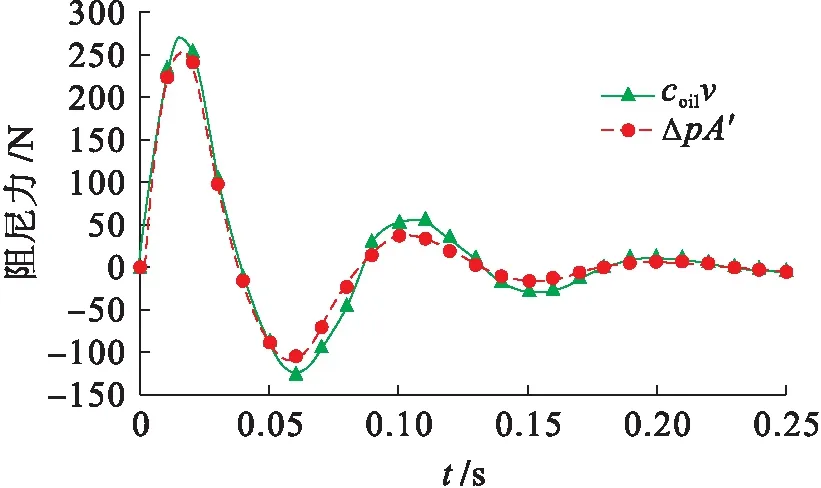
圖6 阻尼力與比較Fig.6 Comparison between damping forces

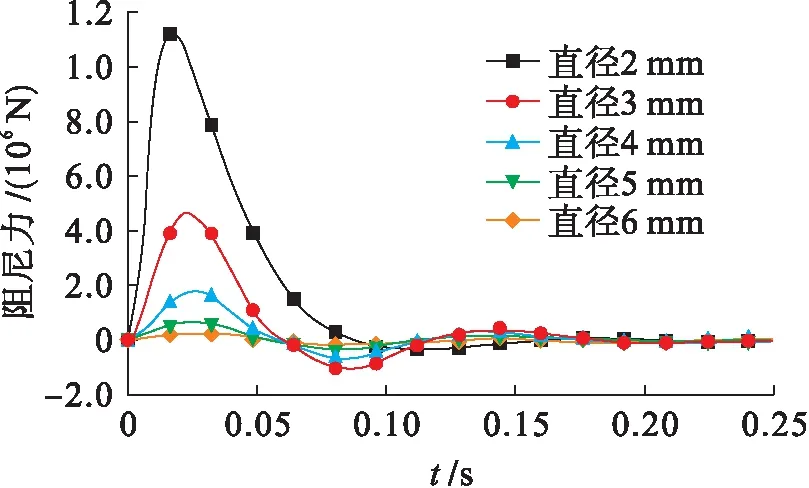
圖7 阻尼孔直徑為2～6 mm時的阻尼力Fig.7 Damping force of damping holes with diameter from 2 mm to 6 mm

由圖7可見，阻尼孔越小產生的阻尼力越大，當阻尼孔直徑為2 mm時，產生的阻尼力最大.當阻尼孔直徑從2 mm增大到3 mm時，對應的阻尼力峰值迅速減小，此過程變化較為劇烈.在實際工程中需要根據隔振系統整體性能指標來選取阻尼孔直徑的尺寸.

3 液壓阻尼力的試驗驗證

3.1 試驗裝置與原理

為了驗證基于AMEsim仿真結果修定的隔振系統數學模型的正確性，設計隔振系統的試驗裝置如圖8所示.該試驗裝置由底座、隔離部分、被隔離設備和液壓阻尼器四部分構成，液壓阻尼器的缸筒通過法蘭盤與隔振系統的底座剛性連接，由液壓阻尼器中帶沖擊頭的活塞桿支撐被隔離設備.圖9為垂向雙波沖擊臺原理簡圖.采用500 kg垂向雙波沖擊試驗機進行沖擊試驗，該試驗機主要由基礎系統、液壓系統、機械系統和測控系統等幾部分組成[16]，其主要工作原理為：沖擊前由蓄能器存儲沖擊所需能量，沖擊時蓄能器中的能量在正波液壓系統控制下釋放，驅動沖擊錘撞擊沖擊臺產生正波沖擊；當沖擊臺向上運動達到最大速度時，阻尼缸在負波液壓系統控制下對沖擊臺實施制動產生負波沖擊，使沖擊臺減速運動直到停止.

圖8 雙出桿孔隙式液壓阻尼器試驗裝置Fig.8 Test device of double-out rod hydraulic pore-type viscous damper

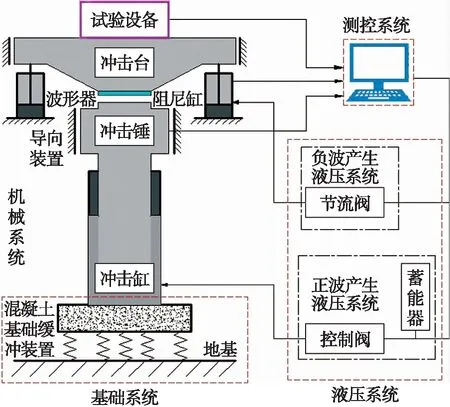
圖9 垂向雙波沖擊臺原理簡圖Fig.9 Schematic principle diagram of vertical double wave shock table

調整試驗裝置各部分參數使其同仿真計算參數一致，通過垂向雙波沖擊試驗機施加與仿真相同的沖擊激勵進行沖擊試驗驗證.

3.2 沖擊試驗與仿真數據對比

圖10、11為當沖擊試驗機施加特定沖擊激勵(參數見表1)時，液壓隔振系統加速度響應和相對位移響應的仿真計算與試驗結果時域歷程對比曲線.不同沖擊載荷激勵下，液壓隔振系統的相對位移響應和加速度響應試驗峰值數據與仿真計算誤差如表4所示.

結合圖10、11和表4可知，在40g輸入載荷作用下試驗測得的系統加速度響應峰值為20.67g，仿真計算誤差為2.5%；試驗測得的系統相對位移響應峰值為13.11 mm，仿真計算誤差為2.97%，均在誤差允許范圍內.可見，液壓隔振系統通過試驗得到的相對位移響應和加速度響應時域歷程曲線與仿真計算結果具有較好的一致性.由表4可知，在40g～70g輸入載荷作用下系統的相對位移響應和加速度響應峰值隨沖擊載荷的變化趨勢與仿真計算具有較好的一致性，仿真計算與試驗結果的最大誤差為5.48%，遠遠小于20%的允許誤差范圍，證實了本文數學模型的準確性.

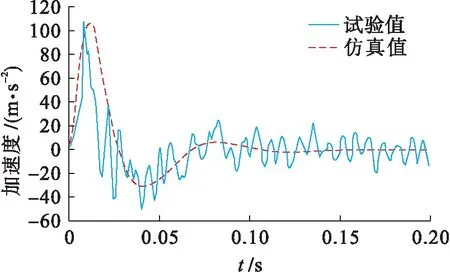
圖10 系統加速度響應對比Fig.10 Comparison of acceleration response of system

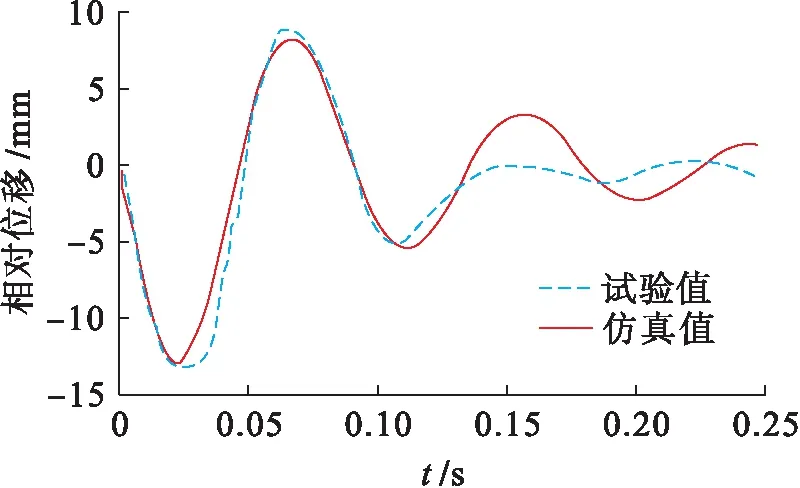
圖11 系統相對位移響應對比Fig.11 Comparison of relative displacement response of system

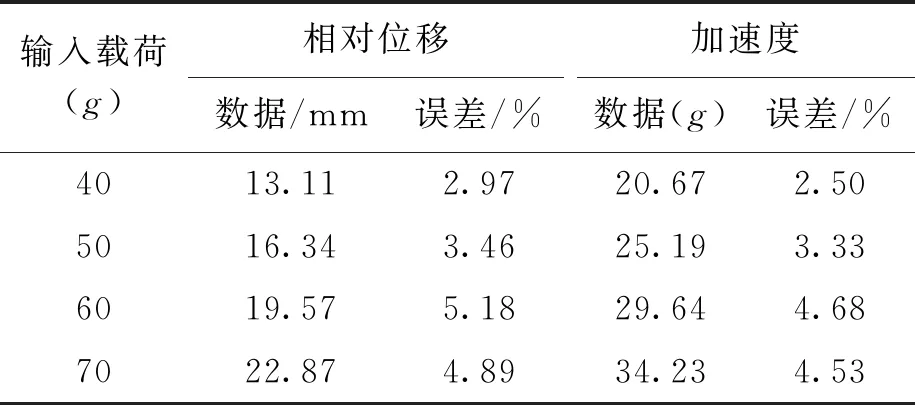
表4 不同載荷下隔振系統沖擊響應數據Tab.4 Shock response data of vibration isolation system under different loads

4 結 論

通過以上分析可以得出如下結論：

1) 孔隙式液壓隔振系統數學模型的建立過程中考慮了液壓阻尼力的非線性特征，提出了利用AMESim軟件仿真計算液壓阻尼器阻尼力的有效方法，并確定了數學模型中的流動指數；

2) 基于AMESim軟件計算液壓阻尼器阻尼力的方法相比常規試驗法節約了成本，縮短了液壓隔振器的開發周期；

3) 利用MATLAB軟件對液壓隔振系統的數學模型進行了仿真計算，其結果與試驗數據相比具有較好的一致性，仿真計算誤差均在允許范圍內，表明本文建立的隔振系統數學模型能夠準確反映隔振系統各參數特性.

綜上所述，在設計艦載設備用液壓隔振裝置時，通過AMESim軟件仿真來確定液壓阻尼器阻尼力的方法是切實可行的，能夠在仿真基礎上對試驗做出較為準確的預測.這種方法為液壓隔振系統的理論研究提供了行之有效的理論依據.