大型復雜機電加工系統(tǒng)緩沖阻尼動力學性能分析*
劉 浩, 姜長青
(1. 衡水學院 物理與電子信息系, 河北 衡水 053000; 2. 清華大學 航天航空學院, 北京 100084)
空間對接技術中,根據(jù)結構方式的不同可以將對接機構分為桿錐式對接機構和周邊式對接機構[1].對接機構在兩個航天器進行空間對接時會發(fā)生接觸和撞擊的現(xiàn)象,為了確保航天器安全和對接成功,需要采用一種有效的手段來對撞擊能量進行阻尼與緩沖.一般情況下采用緩沖阻尼系統(tǒng)完成上述功能,根據(jù)不同的緩沖阻尼元件,系統(tǒng)可分為獨立式液壓緩沖阻尼系統(tǒng)和差動式機電緩沖阻尼系統(tǒng)[2].差動式機電緩沖阻尼系統(tǒng)被人們所重視,被廣泛使用到國際空間站中,但差動式機電緩沖阻尼系統(tǒng)的結構較為復雜,在該系統(tǒng)中存在上百個能夠運動的部件.相關專家學者對緩沖阻尼動力學性能進行了研究,并取得了良好的研究成果,文獻[3]進行了嵌入式共固化網格阻尼結構復合材料的動力學性能研究,建立嵌入式共固化網格阻尼結構復合材料的有限元數(shù)值模擬模型,用改進的應變能法分析了該網格結構的阻尼特性.文獻[4]進行了非線性阻尼非線性剛度隔振系統(tǒng)隨機動力學特性研究,通過求解FPK方程等效非線性隨機振動方程來研究非線性隔振系統(tǒng)在隨機激勵下的隔振性能,并使用路徑積分和Monte-Carlo數(shù)值法進行驗證.
采用當前方法研究機電緩沖阻尼系統(tǒng)緩沖阻尼動力學性能時,并不能準確得到機電加工系統(tǒng)的動力學方程和運動約束方程.為了解決上述問題,本文提出了機電加工系統(tǒng)緩沖阻尼動力學性能分析方法.
1 機電加工系統(tǒng)結構組成與運動方程
1.1 機電加工系統(tǒng)結構組成
差動式緩沖阻尼系統(tǒng)作為傳動、阻尼和緩沖的直接控制機構,由驅動裝置、捕獲環(huán)、副桿聯(lián)系組合和絲桿聯(lián)系組合四個功能單元組成,機電加工系統(tǒng)的結構如圖1所示.
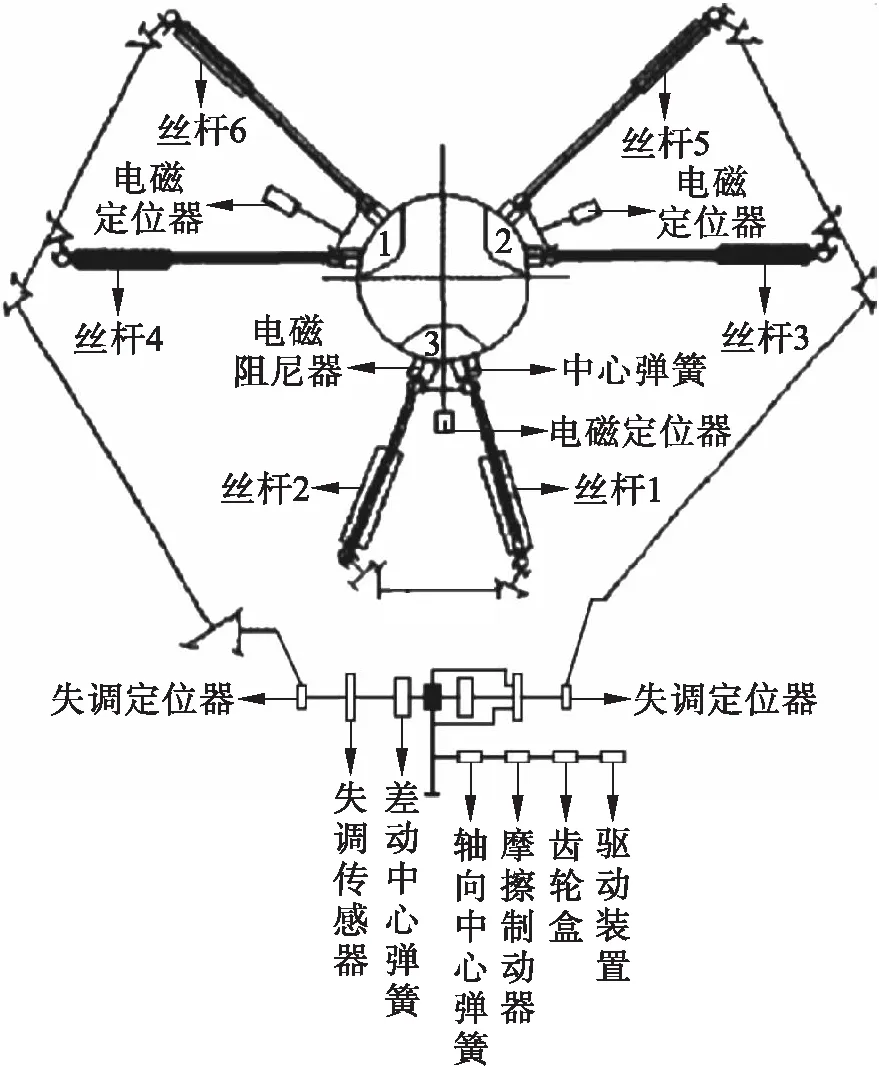
圖1 系統(tǒng)的基本部件分布示意圖Fig.1 Schematic diagram of basic part distribution in system
絲杠聯(lián)系組合是由聯(lián)系齒輪和滾珠絲杠轉換器構成的差動組合;電磁阻尼器和彈簧分別與絲杠聯(lián)系;副桿聯(lián)系是一個差動組合,通常由中間傳動軸和差速器構成,在差速器中裝置雙軸彈簧機構,將始端彈簧集合和摩擦制動器放置在驅動裝置前[5].利用傳動軸和中間齒輪連接各個單元,形成差動式緩沖阻尼系統(tǒng).通過上述部件并根據(jù)合適的運動組合完成對接開始、對接過程中和對接結束后捕獲環(huán)的伸出和拉緊,在對接時保證在6個自由度方向捕獲環(huán)的靈活運動,為捕獲連接提供便利,進而提供有效的阻尼和緩沖,吸收航天器空間對接時由于接觸和撞擊而產生的動能[6].
1.2 機電緩沖阻尼機構的運動方程
1.2.1 彈簧機構
在機電加工系統(tǒng)中總共設置了6個采用平面蝸卷彈簧的彈簧機構.機電加工系統(tǒng)中存在兩種工作形式不同的彈簧,一種是安裝在絲杠組合處的單軸雙向旋轉彈簧K1;另一種是安裝在摩擦制動器前和連接差速器兩端的雙軸雙向旋轉彈簧K2、K3[7].單軸雙向旋轉彈簧和雙軸雙向旋轉彈簧在機電加工系統(tǒng)中的受力變形可分別表示為
(1)
(2)
式中:ki為彈簧的剛度;φ、φ1、φ2為旋轉軸對應的轉角.
1.2.2 電磁制動器
電磁制動器是一種阻尼元件,存在于絲杠聯(lián)系組合中.當電磁制動器的轉速不高時,轉子轉速ω實際上與制動力矩成正比.構建動力學方程時,可用速度的線性函數(shù)代替制動器的阻尼力,用速度的二次齊次函數(shù)代替耗散函數(shù),動力學方程表達式為
(3)
式中:n為電磁制動器在絲杠聯(lián)系組合中的數(shù)量;cij為耗散系數(shù).
1.2.3 摩擦制動器
摩擦制動器在機電加工系統(tǒng)中作為能量吸收元件,由摩擦片、鋼球壓力調整器和旋轉軸構成.摩擦片在鋼球壓力調整器工作下的額定扭矩為Mn,與差速器外殼連接的齒輪在撞擊力的作用下,將扭矩轉移到摩擦制動器前端的彈簧K2中,利用旋轉軸將彈簧產生的力矩傳送到摩擦片上.當額定扭矩Mn大于力矩時,摩擦片保持不動;當額定扭矩Mn小于力矩時,摩擦片隨著旋轉軸開始傳動,撞擊能量通過滑動摩擦消耗.設θ為齒輪在差速器外殼上工作的轉角;k4為彈簧K4對應的剛度,則差速器傳輸力矩可表示為Mk3=k4θ.
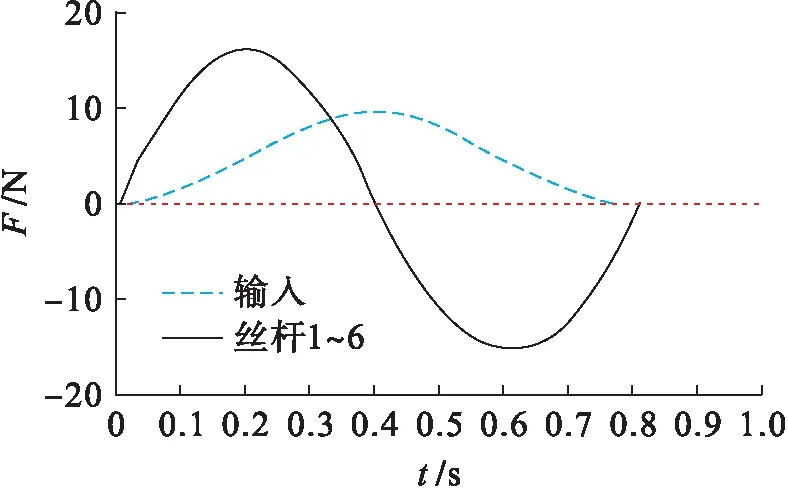
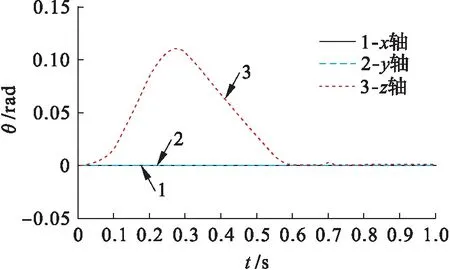
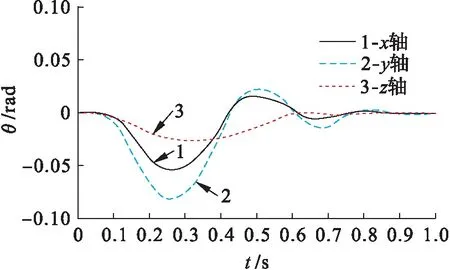
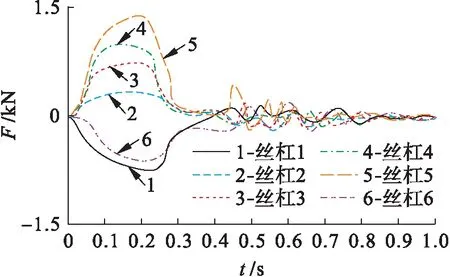
如果Mk3 (4) 式中,f為摩擦系數(shù).如果Mk3≥Mn,摩擦制動器開始工作,旋轉軸此時的轉角為θ2,此時彈性勢能可表示為 (5) 當絲杠不圍著軸線轉動時,絲母轉速ω1和絲杠沿軸線運動速度v之間的關系可表示為 v=ω1d/2π (6) 式中,d為螺旋導程. 根據(jù)速度合成定理,絲杠沿軸線的平均速度與絲杠軸線上任意一點運動速度對應的投影相同[8].假設在絲杠軸線中存在上鉸點和下鉸點,則運動速度可表示為 (7) (8) 式中,isd為傳動比.將式(6)、(7)代入式(8)可以得到 (9) cosβ=H/L (10) 式中:H為下鉸點分布平面與上鉸點分布平面之間的距離;L為下鉸點和上鉸點之間在機電加工系統(tǒng)中的距離,其計算公式為 (11) 其中,Lyz為下鉸點分布平面中距離L的投影距離. 將式(10)、(11)代入式(9)中得到 (12) 式中,θ0、L0為積分常數(shù). 假設軸向力Fx作用于機電加工系統(tǒng)中,此時摩擦制動器的狀態(tài)為鎖定狀態(tài).設m為在不考慮其他構件質量基礎上固聯(lián)構件和捕獲環(huán)的質量,由虛功率原理和達朗貝爾原理可得 (13) 式中:δ為剛性系數(shù);TB為始端彈簧在機電加工系統(tǒng)中的力矩. 將式(9)轉變?yōu)樽兎中问剑⑥D變結果代入式(13)中,得到機電加工系統(tǒng)的動力學方程為 (14) 設始端彈簧在機電加工系統(tǒng)中為線性彈簧,其力矩表達式為 Tg=T0+CSθ (15) 式中:CS為彈簧剛度;T0為彈簧預緊力矩. 當始端彈簧處于極限行程時,繼續(xù)增加軸向力會造成摩擦制動器出現(xiàn)打滑的現(xiàn)象[9].假設始端彈簧機構在此時轉變?yōu)閯傂詡鲃訖C構,不考慮摩擦制動器在機電加工系統(tǒng)中的傳動慣量,則可得到機電加工系統(tǒng)動力學方程對應的變分形式為 (16) (17) 在式(11)和式(12)的基礎上,將變分形式導入,則可得輸出機電加工系統(tǒng)的動力學方程為 (18) 根據(jù)得到的動力學方程對機電加工系統(tǒng)緩沖阻尼動力學性能進行分析,獲得捕獲環(huán)在不同撞擊力影響下機電加工系統(tǒng)的運動學響應.實驗分為實際實驗與仿真實驗兩部分,實驗持續(xù)時間為一個月,通過實際實驗獲取機電加工系統(tǒng)捕獲環(huán)角位移對應的位移響應、絲桿鉸鏈在階躍型撞擊下的約束響應等實驗參數(shù).仿真實驗軟件為MATLAB7.0軟件,操作系統(tǒng)為Windows 10,內存為24 GB,機電加工系統(tǒng)基本參數(shù)如表1所示. 同軸拉緊或同軸推出時,機電加工系統(tǒng)要求各個絲桿構件在機電加工系統(tǒng)中的受力均勻.各個絲桿構件在機電加工系統(tǒng)聯(lián)系齒輪、彈簧軸鎖定且同軸推出情況下的受力情況如圖2所示. 表1 復雜機電加工系統(tǒng)基本參數(shù)Tab.1 Basic parameters for complex electromechanical machining system 圖2 各個絲桿構件的受力情況Fig.2 Stress condition of each screw component 由圖2可知,6根絲桿工作變化曲線是完全重合的,表明在這種工況下,各個絲桿在機電加工系統(tǒng)中的受力是均勻的,機電加工系統(tǒng)的緩沖阻尼符合特殊功能的要求. 在滾動方向撞擊力的影響下,機電加工系統(tǒng)中捕獲環(huán)角位移對應的位移響應曲線如圖3所示. 圖3 捕獲環(huán)位移對應的響應曲線Fig.3 Response curves corresponding to capture ring displacement 由圖3可知,在x軸方向和y軸方向捕獲環(huán)的角位移都是零,只存在捕獲環(huán)繞z軸得到的角位移.捕獲環(huán)的運動響應特征在機電加工系統(tǒng)中為純滾動,通常情況下還在z軸方向中存在極小的線位移.通過進一步的分析和計算可知,相同絲桿組中存在的兩個絲桿在機電加工系統(tǒng)中的受力情況不同,但在不同絲桿組中的構件存在相同受力響應情況,表明機電加工系統(tǒng)在滾動方向撞擊影響下的響應較為單純. 圖4和圖5為機電加工系統(tǒng)在階躍型函數(shù)影響下捕獲環(huán)角位移的響應和絲桿鉸鏈約束力的響應,其中階躍型力函數(shù)G(t)的表達式為 G(t)=N(s1,0,0,0.1,200)- N(s2,0.2,0,0.3,2 000) (19) 式中:N為一階導數(shù)對應的階躍函數(shù);s1為絲桿鉸鏈約束力的初始響應參數(shù);s2為捕獲環(huán)角位移的初始響應參數(shù). 圖4 捕獲環(huán)在階躍型撞擊力下的角位移響應曲線Fig.4 Angle displacement response curves of capture ring under step impact force 圖5 絲桿鉸鏈在階躍型撞擊力下的約束響應曲線Fig.5 Constrained response curves of screw hinge under step impact force 由圖4和圖5可知,在不同工況下機電加工系統(tǒng)能夠起到緩沖衰減外部作用力的效果,在合理參數(shù)配置前提下可以有效地耗散和吸收空間6個自由度方向的作用能量. 本文分析了機電加工系統(tǒng)緩沖阻尼動力學性能,并利用對應的分析方法得到機電加工系統(tǒng)的運動學方程,根據(jù)方程進行實例分析,證明了機電加工系統(tǒng)可以有效地吸收并緩沖空間6自由度方向的作用能量.采用機電加工系統(tǒng)緩沖阻尼動力學性能分析方法可以有效、準確地分析機電加工系統(tǒng)的運動情況,本文將機電加工系統(tǒng)的阻尼特性和剛度特征作為機電加工系統(tǒng)開發(fā)和設計的依據(jù),為該系統(tǒng)的進一步發(fā)展奠定基礎.2 緩沖阻尼動力學性能分析
2.1 運動學分析


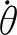
2.2 動力學方程
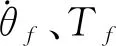
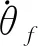
3 實例與仿真分析

4 結 論

