基于大數據分析的非線性網絡流量組合預測模型*

許繪香， 曹 敏， 馬瑩瑩

(鄭州工程技術學院 信息工程學院， 鄭州 450044)

由于計算機網絡技術和互聯網技術的飛速發展，網絡通信業務越來越多，為了滿足網絡用戶對不同業務的通信需求，需要對當前網絡通信流量進行有效管理[1].網絡流量預測模型的構建是實現網絡管理和流量控制的基礎工作，高精度的預測模型不僅能夠準確地提供未來時段的流量數據，同時也可應用于擁塞控制、僵尸檢測等多個方面[2].高精度預測模型具有精確描述網絡流量變化特性的能力，例如非線性、周期性和長相關性等.當前的流量預測模型僅能對線性網絡流量進行預測，無法準確描述網絡流量變化特性，應用范圍有限，已不適用于大規模網絡流量的預測和分析[3].組合模型能夠擬合多個單一預測模型的優點，更精確地描述網絡流量特征，已成為該領域的研究熱點，受到了廣泛關注[4-5].

國內學者在網絡流量預測方面已取得較好成果[6].殷榮網[7]采用最小二乘支持向量機(LSSVM)算法構建了網絡流量預測模型，利用模糊均值聚類算法對網絡流量聚類進行劃分，并去除其中孤立樣本點，將聚類結果構建成訓練集，將其輸入至LSSVM中進行學習并構建網絡流量預測模型，利用人工蜂群算法優化LSSVM模型.大規模網絡流量具有非線性和突發性特點，采用該模型難以精確地描述非線性網絡流量變化趨勢，預測精度較低.

為了解決上述模型存在的問題，提高網絡流量的預測精度，提出基于大數據分析的非線性網絡流量組合預測模型.根據實驗結果可知，運用所提模型對網絡流量進行預測時預測精度較高，能夠滿足大規模網絡環境流量預測精度的要求，有效解決了傳統方法存在的問題.

1 網絡流量數據特性分析

網絡流量是指網絡上傳輸的數據量，由于其數據量規模較大，存在易擁塞、易受攻擊等問題，會導致網絡異常現象的發生.網絡異常，即網絡服務器帶寬不滿足網絡用戶使用流量需求時導致的帶寬擁塞和病毒入侵等，使得真實的網絡流量具有混沌特性[8-9].本文在Matlab環境下搭建實驗平臺，利用NS2仿真軟件獲取網絡流量模擬數據，圖1為采集到的網絡流量時間序列.

圖1 網絡流量原始時間序列Fig.1 Original time series of network flow

通過對該時間序列進行觀測和分析，可以發現網絡流量數據具有如下特性：1)突發性.受到相同局域網內網絡帶寬的影響，實際采集的網絡流量數據具有突發特性.2)周期性.實際采集的網絡流量數據在采集周期內呈現出階段性變化.3)長相關性.圖1所示的網絡流量數據具有相同的統計特性.4)非線性.網絡流量的變化與用戶數量、用戶使用高峰期、網絡路由協議等相關，造成網絡流量的非線性.

綜上可知，網絡流量數據具有突變性、非線性等特點.對非線性網絡流量進行高精度預測，需要對網絡流量數據進行分解，從原始非線性網絡流量時間序列中提取其變化規律.

2 非線性網絡流量組合預測模型

2.1 網絡流量數據分解及重構

對采集的大規模網絡流量數據進行小波分解，獲得多尺度分量，采用混沌理論對分解的多個尺度分量進行重構，獲得網絡流量子序列，具體過程如下：實際采集的網絡流量數據具有混沌特性，從原始非線性網絡流量數據提取其變化規律，重構出等效的分布空間[10].對于實際采集的網絡流量數據xi(i=1，2，…，n)，可通過分析其變化規律重構出一個多維分布空間yi=(xi，xi+θ，…，xi+(m-1)θ)，θ為時間維度，網絡中的流量數據普遍存在噪聲.

對采集的網絡流量數據進行小波分解，即

(1)

利用混沌理論對式(1)分解出的不同分量進行相空間重構，重構出的非線性網絡流量子序列為

(2)

式中，g為相空間維度.

非線性網絡流量時間序列經過快速小波分解，將網絡信號的高低頻部分有效分離，可從中挖掘出網絡流量數據周期性變化趨勢，消除其中突變部分，剩余的高頻部分能夠精確地描述網絡流量數據的變化特征.采用混沌理論對分解的多個尺度分量進行重構，降低了大規模非線性網絡流量數據的預測誤差及計算復雜度.

2.2 模型構建

采用改進鳥群算法優化核極限學習機模型參數，利用優化后的核極限學習機模型分別對重構后的網絡流量子序列進行預測，將各個子序列的預測值進行組合，獲得最終的網絡流量預測結果.

采用改進鳥群算法通過種群個體之間的信息共享機制以及搜索策略最終獲得最優解，具體尋優步驟如下：

1) 覓食行為.鳥類成群覓食時比個體覓食收集到的信息更多，并且覓食效率更高.根據這個原則將網絡單元模擬為種群個體，整體網絡體系模擬為種群.通過混沌映射初始化種群個體τ在D維搜索空間內的初始位置，每個個體依據歷史搜索經驗以及種群經驗覓食.在種群個體位置更新階段，引入隨機慣性權重避免陷入局部最優，同時根據隨機慣性權重值對種群中個體的認知因子C，C∈(Cmin，Cmax)，以及加速因子S，S∈(Smin，Smax)進行動態調整，即

(3)

ω=ωmin+(ωmax-ωmin)rand(0，1)+

σrand(0，1)

(4)

(5)

(6)

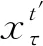
2) 警惕行為.種群中的每只鳥在搜索過程中，都會試圖靠近種群中心位置飛行.警惕性強的個體相比警惕性低的個體更容易向種群個體中心飛行，彼此之間相互競爭，根據此原則可得

(7)

式中：A1為搜索空間影響因子，A1∈(0，1)；A2為搜索空間干擾影響因子；meanj為群體第j維平均位置；pk，j為種群中搜索空間第j維的平均位置.

3) 個體飛行行為.鳥群會有規律地飛向某個地點，在飛行過程中，個體會在生產者與索取者之間進行切換，警惕性較低的個體尋找食物屬于生產者，警惕性較高的個體獲取食物屬于索取者，生產者以及索取者能夠脫離種群，根據此原則可得

(8)

基于改進的鳥群算法網絡流量子序列預測模型可得

Lrand(0，1)

(9)

式中：L為索取者通過生產者尋找食物的因子；f為正則化參數.

基于改進的鳥群算法構建的網絡流量子序列模型可以最小化輸出權值和訓練誤差，即

(10)

式中：LE為核極限學習機模型輸出權值；β為隱含層輸出權值向量，β∈[0，2]；h(xτ)為隱含層輸出結果；ξτ為訓練輸出誤差.依據模型最優化條件可求解獲得

(11)

式中：H為隱含層輸出矩陣；T為目標值矩陣.依據Mercer’s條件對重構后的網絡流量子序列進行預測，其子序列流量預測矩陣為

ΩE=βh(xτ)h(xj)=K(xτ，xj)

(12)

式中，K(xτ，xj)為子序列流量數據預測函數.利用改進的鳥群算法整合各個子序列的預測值，并對正則化參數進行優化，提升預測精度，最終的網絡流量預測模型為

(13)

3 實驗結果與分析

為了測試基于大數據分析的非線性網絡流量組合預測模型的性能，仿真實驗在Intel四核2.8 GHz CPU，4 GB內存，操作系統為Windows7硬件配置電腦下進行，利用VC++軟件實現仿真實驗.仿真實驗來自NS2軟件提供的實際網絡流量數據，共2 000個數據點，如圖2所示.將實際采集的網絡流量數據劃分為兩組，第一組含有1 500個流量數據，將其作為訓練數據集；第二組含有500個流量數據，將其作為測試數據集.

分析圖2a可知，訓練數據集中的網絡流量數據具有非線性的特點，數值變化幅度較大，并且變化幅度較大的流量數據會掩蓋變化幅度較小的流量數據；圖2b測試訓練集中的網絡流量數據雖少，但是也呈現出非線性的變化特點.為了從采集的網絡流量數據樣本中獲取其變化規律，對圖2中的流量進行歸一化處理，即

圖2 實驗數據變化情況Fig.2 Change of experimental data

(14)

式中：xmax和xmin分別為歸一化處理后的流量數據最大值和最小值；x為原始網絡流量數據值.

為了使仿真實驗的驗證結果更具有說服力，選取文獻[7]模型、文獻[8]模型作為對比模型，將均方根誤差(RMSE)、平均相對百分比誤差(MAPE)作為評價指標對不同預測模型的性能進行評價，其表達式分別為

(15)

(16)

網絡流量受到用戶所屬局域網網絡帶寬、瀏覽行為、業務種類以及上網時段等因素的影響，具有混沌性、非線性、突變性.針對這些特性，在構建網絡流量組合預測模型前，利用混沌理論計算仿真對象的延遲時間以及嵌入維度，得到的最優延遲時間t以及嵌入維度m結果如圖3所示.

分析圖3可知，最優延遲時間為t=5，最優嵌入維度為m=4.選定t=5、m=4對網絡流量數據進行重構，獲得網絡流量樣本數據，并將其劃分為訓練集和測試集.

圖3 延遲時間和嵌入維度的計算Fig.3 Calculation of delay time and embedded dimensions

將非線性網絡流量訓練集輸入到核極限學習機模型中進行學習，采用改進鳥群算法優化核極限學習機模型，并構建組合預測模型，預測結果以及預測誤差的變化如圖4所示.

圖4 所提模型單步預測結果Fig.4 One-step prediction results of as-proposed model

分析圖4可知，采用本文模型所得單步預測的流量值與實際網絡流量值較為接近，可高精度地描述網絡流量數據非線性變化特點，預測精度較高.結果表明，通過對采集的網絡流量數據進行小波分解，將分解后的網絡流量子序列進行相空間重構，并將重構結果輸入至核極限學習機中，利用改進鳥群算法對核極限學習機模型進行優化，構建的組合預測模型是有效的.

所提模型與文獻[7]模型、文獻[8]模型所得的多步預測誤差結果如表1所示.

表1 不同模型單步預測精度對比Tab.1 Comparison of single-step prediction accuracy obtained by different models

分析表1結果可知，與文獻[7]模型以及文獻[8]模型相比，本文模型預測誤差最小，有效提高了預測精度，更適用于具有復雜特性的網絡流量預測.

對于具有非線性突變特性的網絡流量數據，對其進行高精度預測需要提前一定的時間，多步預測網絡流量數據具有實際意義.采用本文模型對網絡流量數據進行多步預測，獲得的預測結果與預測誤差變化曲線如圖5所示.

圖5 本文模型多步流量預測結果Fig.5 Prediction results of multi-step flow obtained by as-proposed model

分析圖5可知，在先獲知前幾步流量數據變化趨勢的前提下，本文模型預測結果與實際網絡流量變化趨勢幾乎完全吻合，兩者之間差值較小，且變化較為平穩，能夠將預測誤差控制在8%以下，滿足大規模網絡環境流量預測精度的要求.

本文模型、文獻[7]模型以及文獻[8]模型的多步預測誤差結果如表2所示.

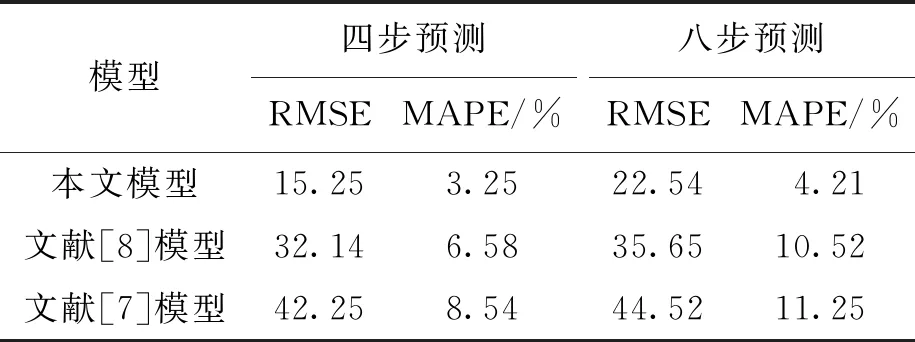
表2 不同模型多步預測誤差結果對比Tab.2 Comparison of multi-step prediction error results obtained by different models

通過對表2結果進行分析可獲得以下結論：隨著網絡流量預測步數的不斷增加，本文模型以及對比模型的預測誤差逐漸增加，其中文獻[7]模型預測誤差增加的幅度較大，直到第八步預測時，該模型預測誤差達到了11.25%，難以精確地描述網絡流量數據階段性變化趨勢，且預測誤差較大，所得結果沒有實際應用價值.相對于文獻[7]模型，文獻[8]模型的預測精度較高，降低了網絡流量預測誤差，但該模型存在計算復雜度高、訓練時間長等問題，難以滿足大規模網絡流量數據的在線預測要求.

4 結 論

網絡流量受到帶寬擁塞和病毒入侵等多種因素的影響，具有非線性、周期性、長相關性等變化特征，傳統的預測模型預測精度較低，針對此問題，提出一種組合預測模型.通過對預測結果進行分析得到以下結論：

1) 相對于文獻[7]、文獻[8]模型，本文模型預測結果的評價指標均更優，說明所提方法克服了當前預測模型存在的精度低的問題，更適用于大規模網絡流量預測.

2) 相對于文獻[7]、文獻[8]模型，本文模型預測精度有所提高，這表明采用快速小波分析算法對網絡流量進行多尺度分解，可以準確挖掘出網絡流量數據階段性變化特征，通過網絡流量子序列表示網絡流量的多層次變化特性.

3) 從圖4～5中給出的網絡流量預測結果來看，所提模型獲得的網絡流量預測值與實際值幾乎完全吻合，變化趨勢基本相同，說明所提模型預測精度較高.