塔梁分離式懸索橋動力及抗震性能*

黎子榮， 劉立鵬， 張楊怡， 朱豪軍，2

(1. 哈爾濱工業大學 交通科學與工程學院， 哈爾濱 150090； 2. 浙江省交通規劃設計研究院， 杭州 310001)

傳統懸索橋的加勁主梁一般支承于兩主塔橫梁上，為適應山區峽谷地形特點，可以設計主梁長度小于塔距，主梁支撐在峽谷兩側穩定巖層上(而非塔下橫梁)，將主梁與主塔完全分離，這樣既能減少工程量降低成本，又能盡最大可能地保護原生環境，與自然和諧相融，湖南矮寨懸索橋是該橋型的首次應用.

崔劍峰等[1]對矮寨大橋進行了結構靜力分析，驗證了懸索橋主纜、吊索、斜拉扣、鋼加勁梁與橋塔等結構均滿足使用要求，介紹了地錨索、斜拉扣以及伸縮縫伸縮量的分析計算方法；馬碧波等[2]詳細敘述了懸索橋地錨索的設計與安裝過程；劉榕等[3]對塔梁分離式懸索橋橋型結構與傳統懸索橋結構進行了最大纜力、加勁梁最大位移、最大吊索力以及橋塔塔頂位移等對比分析，驗證了在湘西特殊地形下選用塔梁分離式懸索橋方案的優越性；余崇[4]為得到懸索橋在地震動作用下各關鍵截面的應力、位移及損傷情況，模擬了地震動作用下湘西矮寨大橋損傷分析；張新[5]采用了增量分析方法，研究不同損傷指標對關鍵構件易損性的影響規律；王杰等[6]對不同縱向約束體系下懸索橋地震反應影響進行研究；董學智[7]對處于峽谷地區帶地錨索的少塔懸索橋進行了地震動作用下結構響應研究；柳國環、蔡小瑾等[8-10]分析了跨越V形峽谷橋梁的抗震性能；Wang等[11]研究了地質條件對雙塔懸索橋抗震性能的影響；劉長喜[12]對高震區懸索橋動力特性及抗震性能進行了研究；Apaydin等[13]分析了懸索橋在空間變化多支點地震激勵下的響應；Bi等[14]研究了跨峽谷橋梁以減小地震對結構造成的二次效應，在橋面與橋墩之間需設置最小分隔距離；Jiao等[15]研究了隨機地震動作用下大跨度三塔懸索橋的地震響應；Siringoringo等[16]通過對地震監測系統長期全面的觀測與研究，得出了懸索橋在地震作用下的響應；Qi等[17]對處在深峽谷地區的矮寨橋進行了巖石基礎穩定性研究；Sgambi等[18]對大跨度橋梁在空間變化地震動下的結構響應進行了分析；鮑文博等[19]等通過對減震控制效應進行彈塑性能量響應分析，研究結構的減震控制.

本文主要分析以下三方面內容：加勁主梁支承方式的改變會在多大程度上影響懸索橋的動力特性與地震響應；吊跨比的變化對結構動力特性以及抗震性能的影響；輔助地錨索的設置及設置數量對結構動力與抗震性能的影響.

1 工程概況

本文依托實際懸索橋工程——矮寨大橋，該橋跨越大峽谷地形，同時也是世界首例采用塔梁分離結構設計的懸索橋.矮寨橋總體布置如圖1所示(單位：mm).主塔為由塔柱與橫梁組成的雙柱式門式框架結構，塔梁為分離式，主纜孔跨布置為242 m+1 176 m+116 m，垂跨比f/l為1/9.6，上下游主纜中心距為27.0 m，全橋設68對吊索(間距為14.5 m)，3對地錨索，吉首岸(J岸)采用重力錨，茶洞岸(C岸)采用隧道錨.

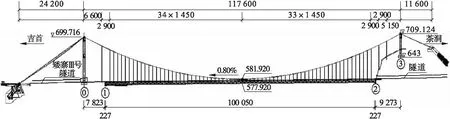
圖1 矮寨大橋布置圖Fig.1 Layout of Aizhai bridge

2 模型建立及驗證

本文采用Ansys有限元軟件進行建模分析，主桁用Beam4梁單元模擬，放大鋼材密度以考慮螺栓、節點板等附加質量影響；考慮主纜垂度效應和大變形等影響確定其初始平衡狀態，采用Link10單元模擬；吊索用Link10單元模擬；考慮到主塔由自重引起的初應變效應，采用Beam4單元模擬；橋面及車輛活載的1/2簡化為質量單元Mass21均布于主梁節點.邊界條件的模擬情況包括：主塔塔底固端約束，主纜兩端固端約束，塔頂位置主纜與塔自由度耦合，地錨索采用巖錨錨固于基巖，主梁設豎向及橫橋向約束.圖2為塔梁分離式懸索橋三維有限元模型.

對所建立的塔梁分離式懸索橋模型進行自重作用下的靜力非線性分析，將其與文獻[4]中模態頻率進行對比，二者的最大相對誤差為3.9%，差異極小，表明本文所建立的有限元模型是合理的.圖3為本文有限元模型與文獻[4]有限元模型模態對比圖.

圖2 塔梁分離式懸索橋三維有限元模型Fig.2 Three-dimensional finite element model of suspensionbridge with separated girder and tower

3 塔梁分離式懸索橋動力特性分析

塔梁分離式懸索橋與傳統懸索橋在結構上的差異必然導致其具有特殊的動力特征，本文研究了主梁支承條件、吊跨比以及地錨索三方面變化對塔梁分離式懸索橋動力特性的影響.

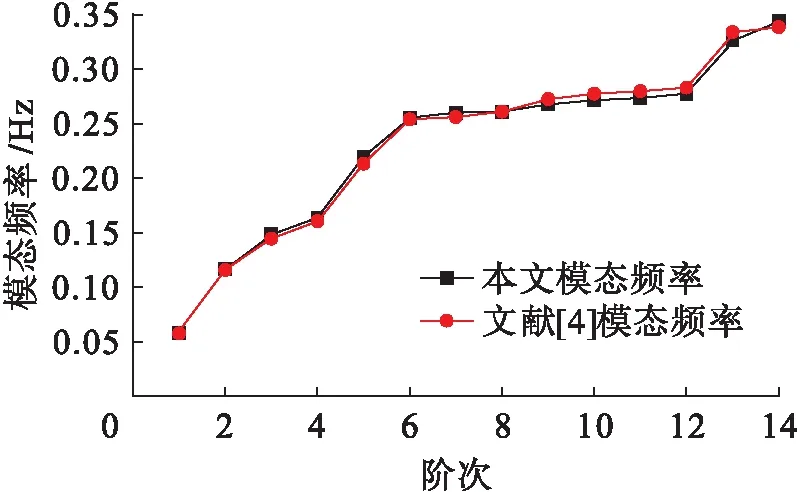
圖3 有限元模型與文獻[4]中矮寨橋模態對比Fig.3 Mode comparison between finite element model and Aizhai bridge in literature [4]

3.1 主梁支撐條件對結構動力特性的影響

采用Block Lanczos求解塔梁分離式懸索橋和傳統懸索橋的自振頻率及對應陣型.表1為兩種懸索橋前20階自振情況，T代表傳統懸索橋，S代表塔梁分離式懸索橋.

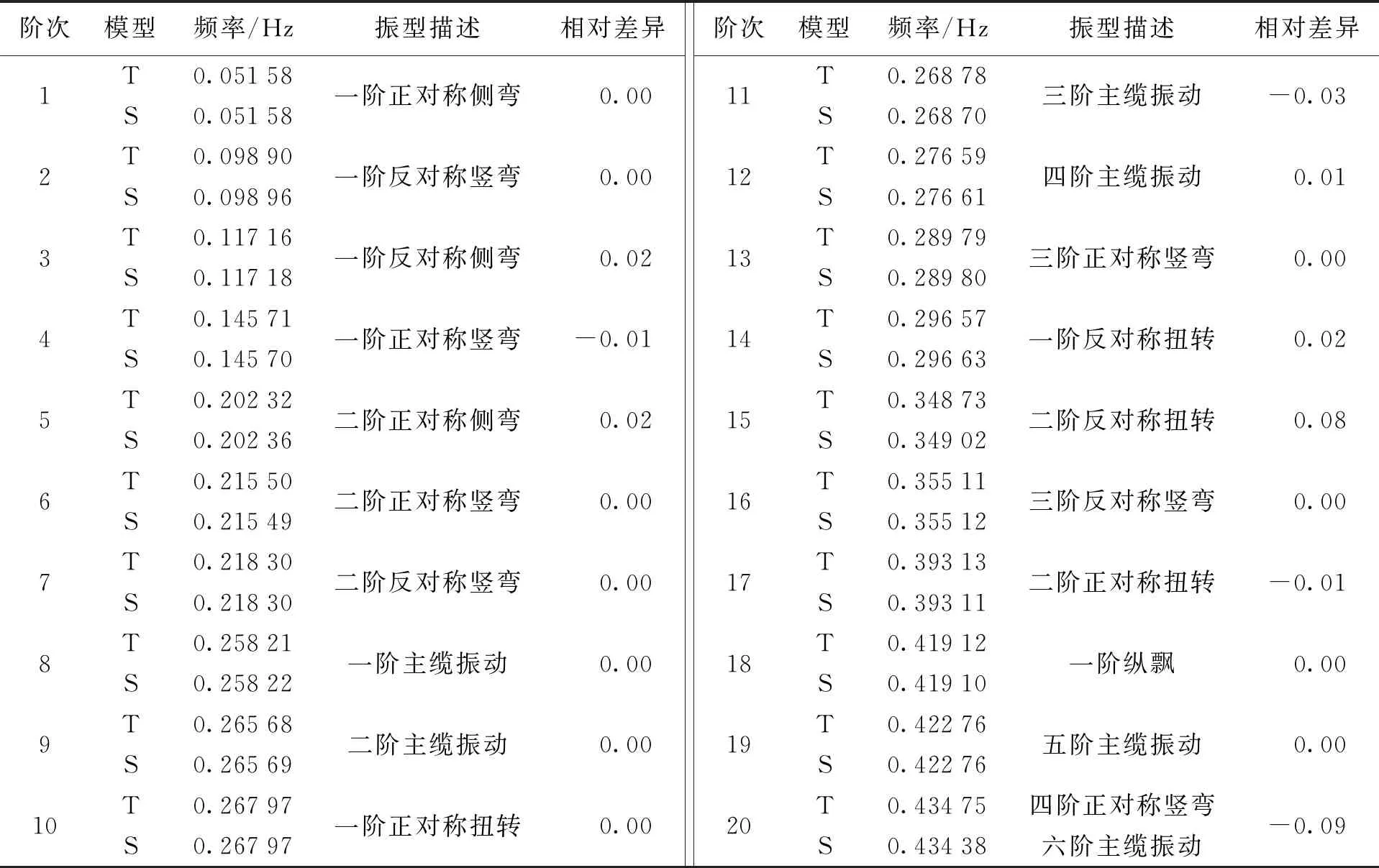
表1 傳統懸索橋與塔梁分離式懸索橋前20階自振特性對比Tab.1 Comparison of first 20 order self-vibration characteristics between traditional suspension bridge and suspension bridge with separated grinder and tower

由表1可知：1)兩橋梁模型基頻相同，且第一階側彎、豎彎、扭轉、主纜振動、縱飄出現的頻率也相同；2)前20階自振特性中，兩模型的自振頻率相差均在0.1以內；3)各階自振特性所對應的振型，僅在頻率密集處出現前后交叉的現象，以主塔為主的振型一般出現較晚.

3.2 吊跨比對懸索橋動力特性的影響

將懸吊主梁兩端部吊索間的距離與兩橋塔之間距離的比值定義為吊跨比，是塔梁分離式懸索橋設計的一個重要參數.設置塔梁分離式懸索橋兩橋塔之間的距離不變，僅改變橋長，同時按原間距加設吊索，設計出吊跨比由0.75增加至0.95的五種塔梁分離式懸索橋模型.圖4為塔梁分離式懸索橋隨吊跨比改變的動力特性圖.

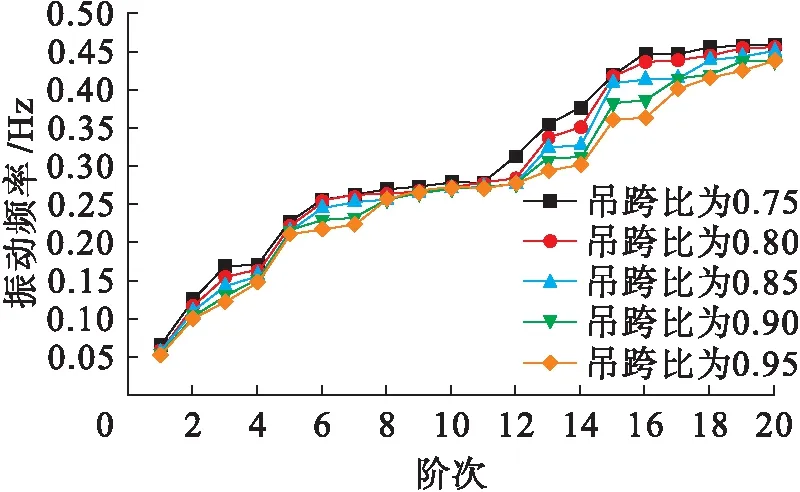
圖4 五種吊跨比前20階頻率比較Fig.4 Comparison of first 20 order frequency underfive ratios of suspension length to span

由圖4可知：1)隨著吊跨比的增加，各階自振特性頻率均有所減小，同時，在前20階自振頻率中，各階振動頻率的變化也不盡相同，頻率之間的差異隨著階次的增加也在逐漸增大，說明吊跨比對懸索橋動力特性的影響會隨著振動階次的增加而被逐漸放大；2)隨著吊跨比減小，側彎(第1、3階)與豎彎(第2、4階)基頻均表現出遞增趨勢，說明隨著吊跨比減小，主梁長度縮短，直接導致主梁側向與豎向抗彎剛度增加.

3.3 地錨索對懸索橋動力特性的影響

以吊跨比為0.75的塔梁分離式懸索橋模型為模型A；在主梁兩側各增設一對地錨索，使廣義吊跨比(即兩端地錨索之間的距離與兩橋塔間距離的比值)為0.85，記為模型B；在主梁兩側各增設兩對地錨索，使廣義吊跨比為0.90，記為模型C.圖5為增設地錨索的模型B及C前20階自振頻率相對于無地錨索模型A的增幅.

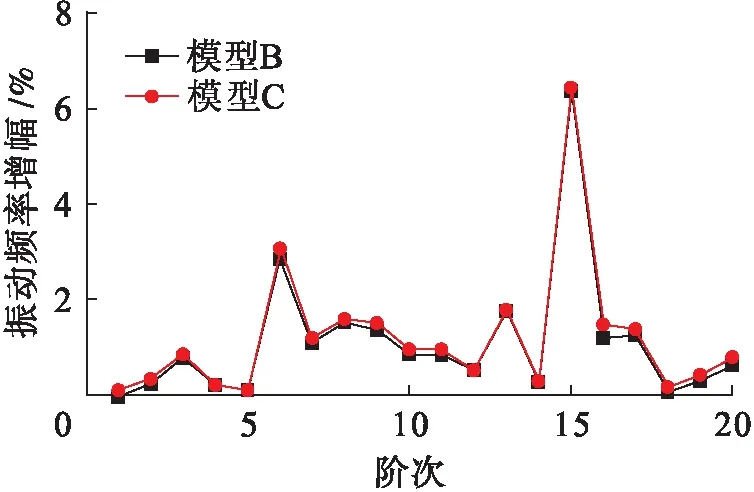
圖5 增設地錨索模型振動頻率增幅Fig.5 Increase amplitude of vibration frequency with ground-anchored cable model

通過圖5可知：1)設置地錨索使結構的各階自振頻率均有所增大，振動頻率增幅最大值為7%，說明增設地錨索提高了懸索橋整體的剛度；2)地錨索設置數量增大，可以提高橋梁整體剛度，使自振頻率增大，但增幅并不如有無地錨索的差異顯著.

4 塔梁分離式懸索橋抗震性能分析

基于橋位地震分組及場地條件，依據規范譜選擇兩條天然波，并生成一條人工波，地震動時程如圖6所示(峰值加速度調整為66 m/s2).

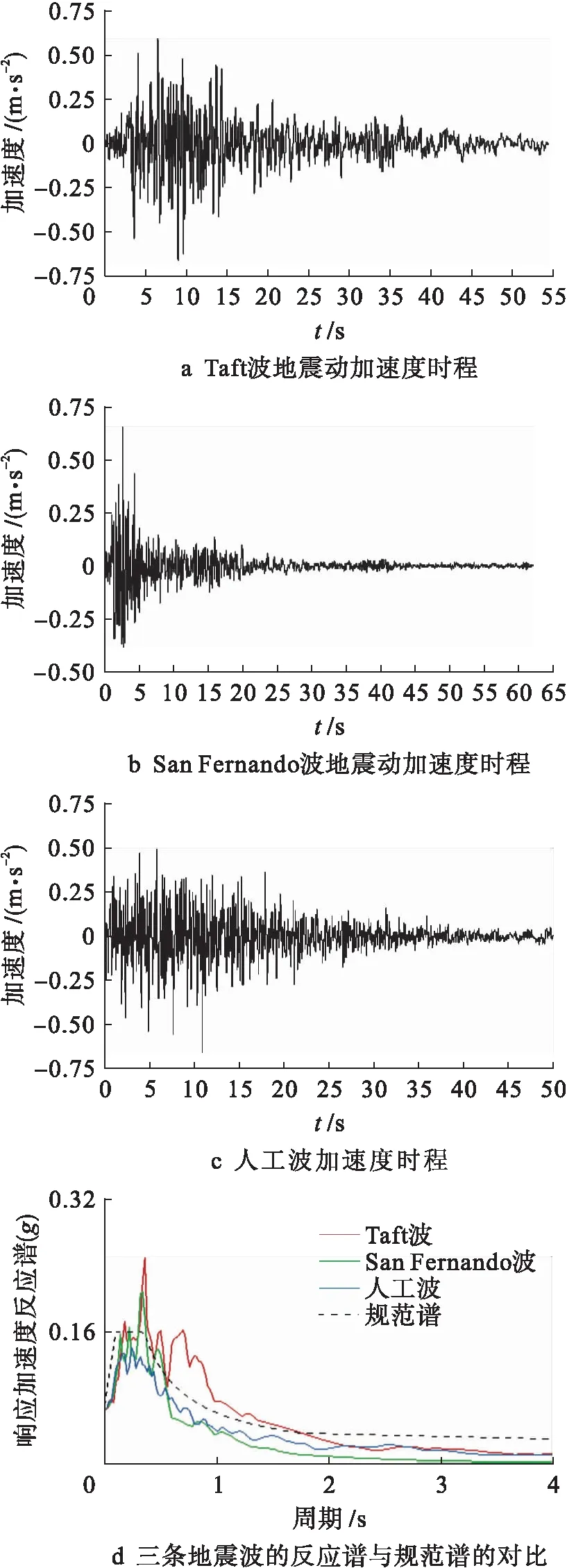
圖6 地震動時程曲線Fig.6 Curves of seismic time history

4.1 塔梁分離對懸索橋抗震性能的影響

雖然單純的塔梁分離式懸索橋相較于傳統的懸索橋在模態分析上的差異可以忽略，但由于地震動具有隨機性和不確定性，需對塔梁分離式懸索橋與傳統懸索橋進行地震動下的響應分析.表2～3分別為T(傳統式)、S(塔梁分離式)懸索橋關鍵位置的結構響應，表3中應力幅是指在每次應力循環中最大拉應力值與最小拉應力或壓應力(拉力為正，壓力為負)的差值的一半.

表2 塔梁分離式懸索橋位移峰值Tab.2 Peak displacement of suspension bridge with separated girder and tower mm

表3 塔梁分離式懸索橋內力峰值Tab.3 Peak internal force of suspension bridge with separated girder and tower

注：應力和應力幅的單位均為MPa.

由表2～3可知：1)縱橋向地震輸入下，塔梁分離式懸索橋與傳統懸索橋的各部件縱向位移基本沒有差異；2)縱橋向和橫橋向地震作用下塔梁分離式懸索橋主塔內力略有輕微減小，對纜索內力基本沒有影響.

4.2 吊跨比對塔梁分離式懸索橋抗震性能的影響

通過對上文建立的吊跨比從0.95至0.75的五個塔梁分離式懸索橋模型進行模態分析，可以看出吊跨比的減小使得橋面長度減小，繼而使主梁抗彎，抗扭剛度明顯增大.本文將對塔梁分離式懸索橋模型在五種不同吊跨比情況下進行抗震性能分析，結果如圖7所示.

從分析結果可知：1)隨著吊跨比增大，主塔剛度增大，振動隨之減弱，縱橋向與橫橋向位移響應與內力響應減小；主纜與吊索的應力響應整體上呈減小趨勢，但變化并不十分明顯.2)隨著吊跨比增大，主梁剛度減小，主梁剛度的變化趨勢與主纜、主塔相反，導致在縱橋向與橫橋向地震作用下，主梁位移響應的變化規律不單調，出現交替；主纜位移響應也受其影響，表現與主梁類似，尤其是接近跨中位置.

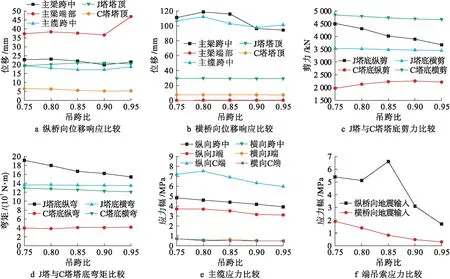
圖7 吊跨比對結構響應的影響Fig.7 Effect of ratio suspension length to span on structural response

4.3 地錨索設置對塔梁分離式懸索橋抗震性能的影響

通過對不同地錨索設置數量的塔梁分離式懸索橋進行模態分析得知，地錨索的設置能提高懸索橋的整體剛度，尤其是主纜剛度；而地錨索設置數量的增加對懸索橋整體剛度幾乎無貢獻.本文將對不同地錨索設置數量的懸索橋模型進行抗震性能分析，位移與內力響應分析結果如圖8所示.

由圖8可知：1)地錨索的設置能很大程度提高懸索橋的整體剛度；2)在橫橋向地震作用下，除其周邊區域的端部纜索外，設置地錨索對結構基本沒有影響；3)地錨索主要影響縱橋向地震響應，設置地錨索減小了主塔位移與內力響應，幅度約為5%，同時降低了主纜與端部吊索的應力響應；4)增加地錨索數量對上述改變基本沒有影響，有時還會削弱上述影響.

圖8 地錨索對結構彈性抗震的影響Fig.8 Influence of ground-anchored cable on structural elastic seismic behavior

5 結 論

本文在主梁的支承條件、吊跨比以及地錨索數量改變情況下，對塔梁分離式懸索橋抗震性能進行影響分析，得出以下結論：

1) 懸索橋支撐條件的改變幾乎不影響自由振動模態.同時，塔梁分離式懸索橋的自振特性頻率隨著吊跨比的增加而逐漸減小；地錨索的設置能較大提高橋梁結構的整體剛度與自振頻率，而增加地錨索的數量對模態影響較為微弱.

2) 在橫橋向地震作用下，地錨索的設置能很大程度抑制主纜以及端部吊索的振動，而對主塔幾乎不產生影響，同時，梁端桿件內力隨著地錨索的設置也有所增大.在縱橋向地震作用下，地錨索的設置能大幅減小主塔位移與內力響應，減小幅度約為5%，能顯著減小梁端桿件內力與端部吊索的振動，而對主纜幾乎無影響.增加地錨索設置的數量對橋梁結構抗震性能影響不大.