500kV 緊湊型線路導線脫冰跳躍計算分析

李 輝 梁盼望 侯長健

（中國能源建設集團湖南省電力設計院有限公司，湖南長沙410007）

0 引言

隨著經濟社會快速發展，輸電線路走廊日益緊張，在路徑走廊擁擠地區采用緊湊型輸電方案具有巨大的社會效益和經濟效益[1]，因緊湊型線路通過壓縮導線相間距離來壓縮輸電線路走廊，因此存在相間距離小于常規輸電線路的固有缺陷，導線脫冰跳躍后相間距離尤為緊張。因此，本文針對500 kV垂直排列雙回緊湊型線路開展舞動不平衡張力計算，對鐵塔進行安全校核，確保線路在舞動區的安全運行。

1 計算模型

1.1 邊界條件

本文研究以500 kV緊湊型線路為例，氣象條件為27 m/s，10 mm覆冰、15 mm覆冰、20 mm覆冰，導線采用等腰倒三角布置，如圖1所示，頂部邊長取6.7 m，腰長取7.2 m。

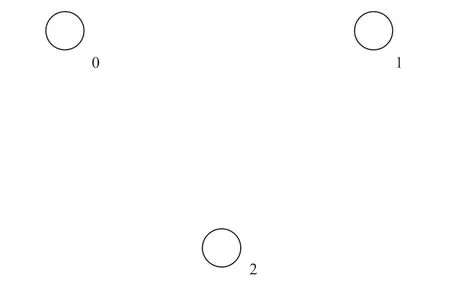
圖1 導線布置方式

1.2 導線參數

500 kV緊湊型線路導線采用6分裂導線型式，考慮的導線型號如表1所示。

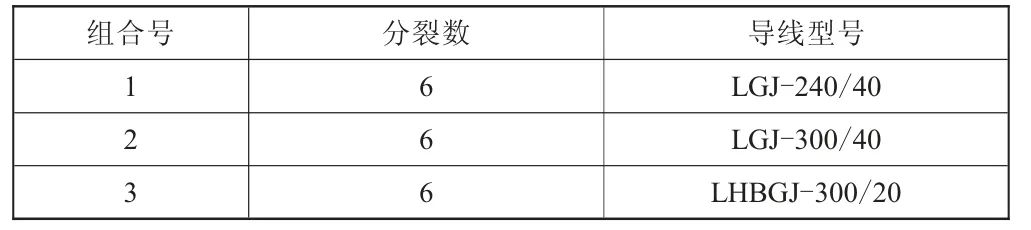
表1 導線分裂數及型號

1.3 導線相間最小空氣間隙

根據《110 kV～750 kV架空輸電線路設計規范》（GB 50545—2010）：海拔500 m以下，500 kV工頻電壓下，相對地的最小空氣間隙為1.20 m。

則500 kV輸電線路，導線相間最小空氣間隙為：1.2×≈2.079 m。

根據《500 kV緊湊型架空輸電線路設計技術規定》[2]（Q/GDW 110—2003），500 kV操作過電壓下，檔距中央的相間最小間隙取為3.85 m。

2 架空線路導線力學計算模型

架空輸電導線的懸鏈線方程為（坐標原點取為懸鏈線的最低點）：

式中：σ0為導線最低點應力（MPa）；g為架空導線的比載（即單位長度導線所承受的載荷與導線截面積的比值，MPa/m）；l為檔距（m）。

導線在不同氣象條件A和B下的應力滿足如下的狀態方程式：

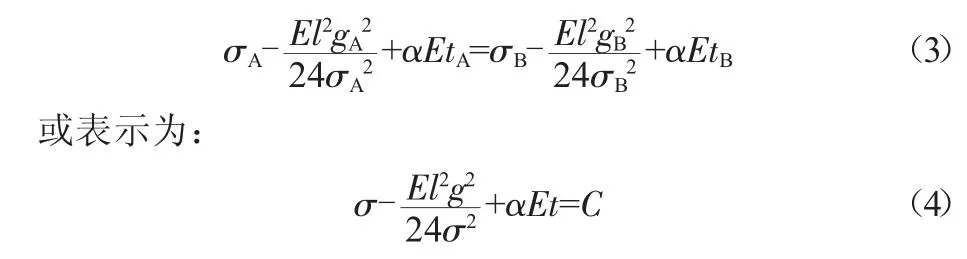
式中：E為架空導線的彈性模量（MPa）；l為檔距（m）；g為架空導線的比載（即單位長度導線所承受的載荷與導線截面積的比值，MPa/m）；σ為導線應力（MPa）；t為溫度（℃）。

3 導線脫冰動力計算

3.1 導線脫冰運動過程

覆冰脫落條件下導線動力計算，是模擬在設計覆冰的條件下（氣溫-5 ℃，風速0 m/s，覆冰厚度15 mm），初始狀態三相導線均為100%覆冰，t=0時刻，下相導線（導線2）的全檔覆冰的50%（以全部覆冰的冰重計）脫落，引起下相導線（導線2）跳起的動態過程。

3.2 脫冰時懸垂串擺動

設計覆冰不均勻脫落條件下，絕緣子串沿Z（導線走向）方向擺動。當架空輸電線路的導線發生覆冰脫落時，除了覆冰脫落導線將向上垂直跳起外，由于覆冰量減小，導線張力將同時減小，將會導致懸垂絕緣子串兩側張力出現不平衡量，使懸掛點絕緣子串發生擺動，另一方面絕緣子串的擺動，將加大導線跳起的高度。

如圖2所示，懸垂絕緣子串兩側分別連接相鄰兩檔導線，在兩側導線張力的共同作用下達到平衡。當兩側導線的覆冰狀況發生變化時，兩側導線的張力也發生變化，懸垂絕緣子串沿Z方向擺動，直至達到新的平衡。

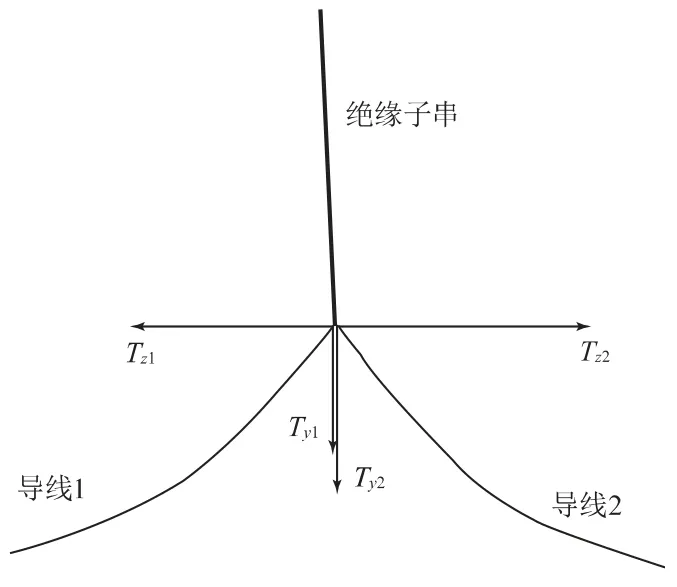
圖2 懸垂絕緣子串的受力及平衡

根據受力平衡原理，導線懸掛點處所受合力為0，即兩側導線張力及絕緣子串的拉力的總合力為0，可得：

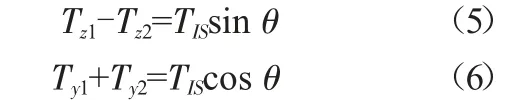
式中：TIS為絕緣子串的拉力（N）；θ為絕緣子串與垂直方向的偏轉角。

3.3 連續檔導線脫冰計算模型

為了準確分析覆冰脫落情況下的導線運動規律，有必要建立多檔導線模型。如圖3所示，考慮2N+1檔的導線模型，2N+1檔導線為一個耐張段，兩側由耐張串懸掛，內部檔間由懸垂串懸掛。

假定多檔導線模型中，各懸掛點間無高差，且假設串1～N及N+2～2N+1共2N檔的檔距均為400 m，第N+1檔為脫冰檔，檔距為300～1 000 m。

4 計算結果

導線不同脫冰率下脫冰跳躍計算結果如表2、表3所示。

由表2、表3計算結果可見：

（1）導線發生覆冰脫落后，由于不平衡張力，導線及懸垂絕緣子串將會發生Z向偏移。

（2）3種型號導線LGJ-300/40、LGJ-240/40、LHBGJ-300/20，在相同的覆冰脫落條件下，大檔距時，就最大跳起高度而言，LGJ-300/40小于LGJ-240/40，LGJ-240/40小于LHBGJ-300/20，即LGJ-300/40抗脫冰跳動性能最好。

（3）兩種脫冰工況，嚴重程度排序為：50%覆冰瞬時脫落＞25%覆冰瞬時脫落。

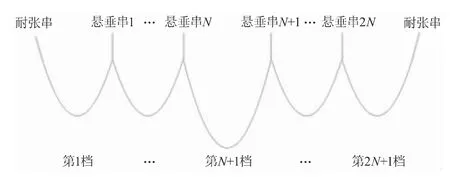
圖3 多檔導線模型

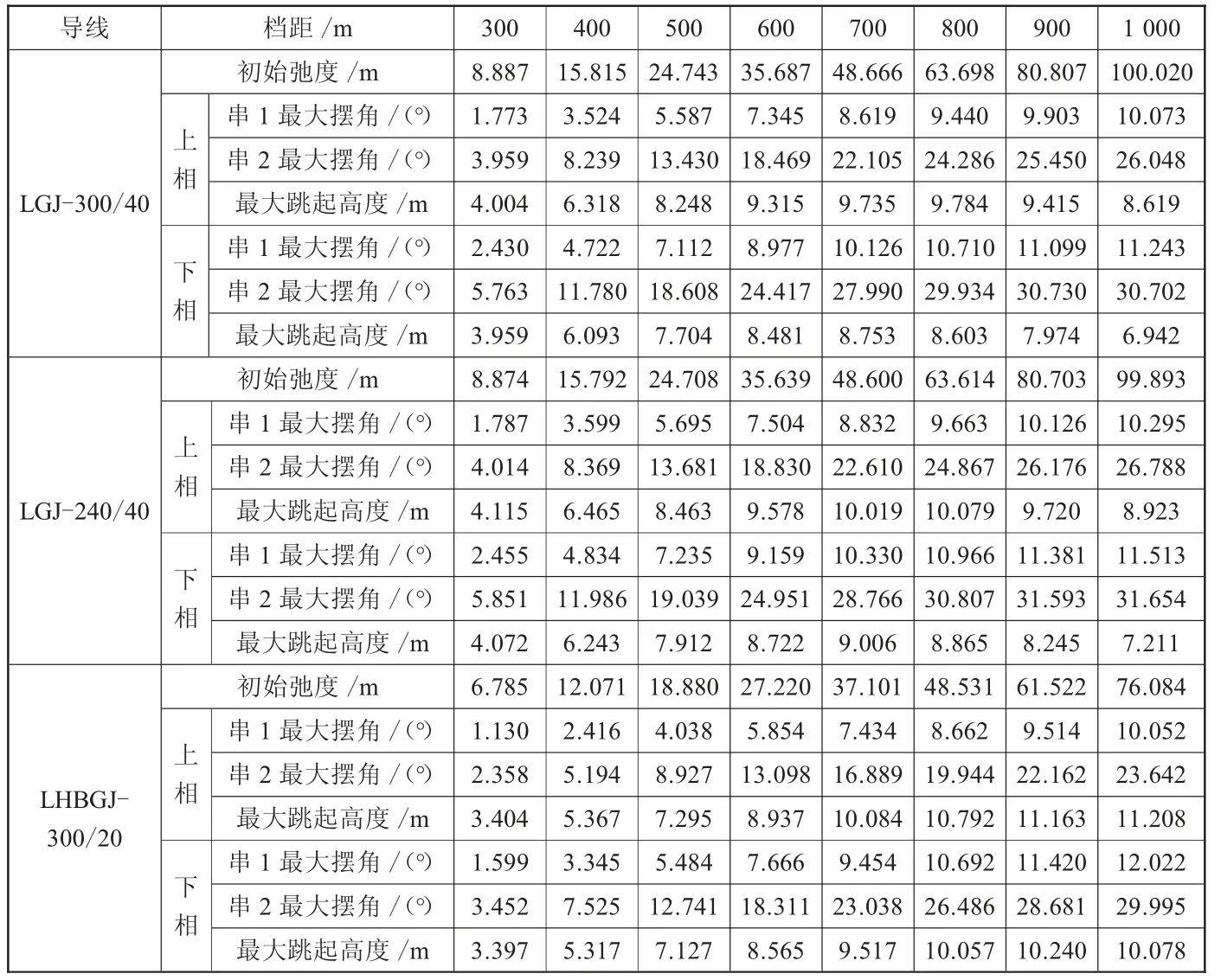
表2 50%覆冰瞬間脫落的動力計算結果（5檔）

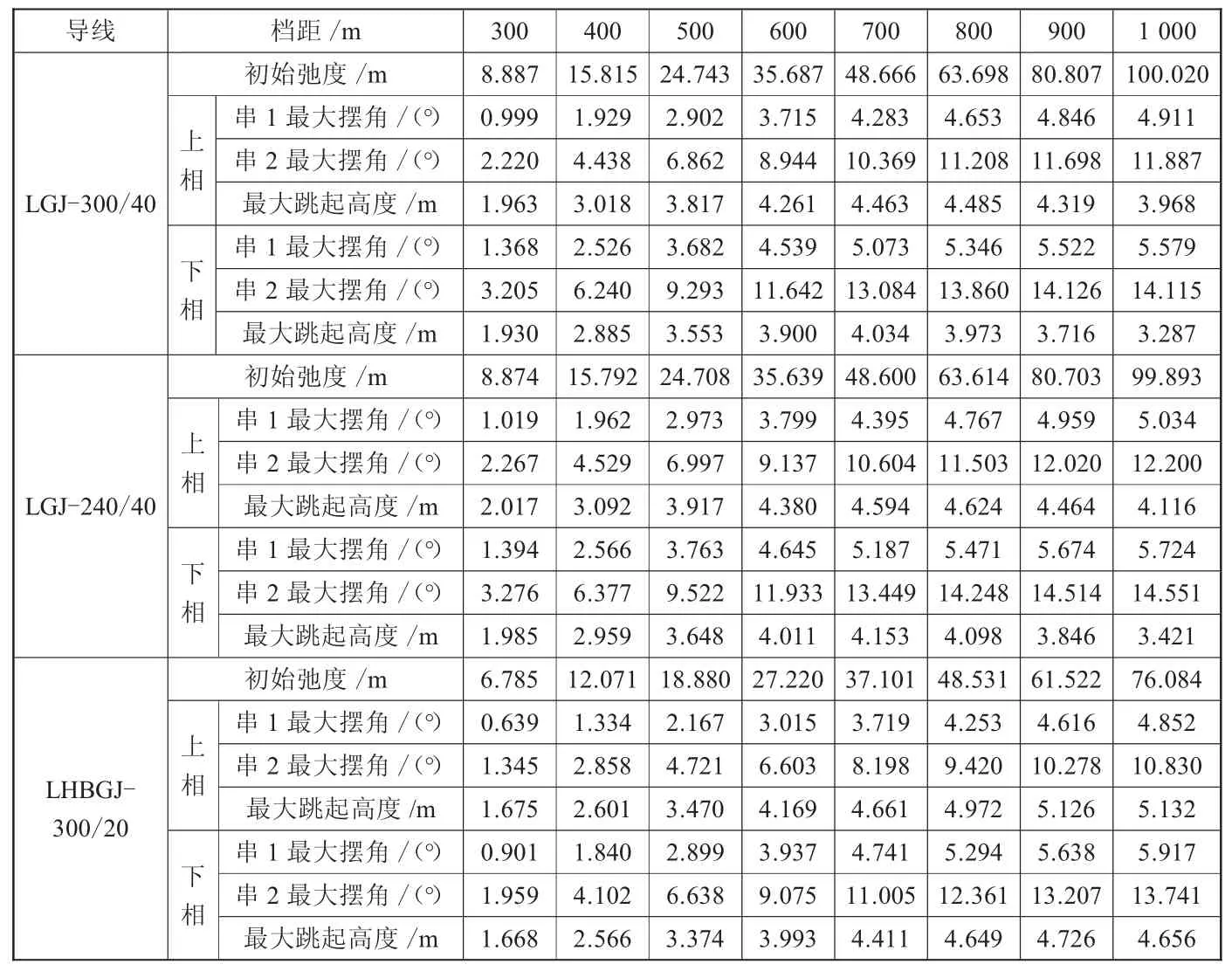
表3 25%覆冰瞬間脫落的動力計算結果（5檔）

5 結語

本文針對500 kV緊湊型線路開展導線脫冰跳躍計算分析，結果表明，導線發生覆冰脫落后，由于不平衡張力，將會使導線及懸垂絕緣子串發生偏移，不同導線的脫冰跳躍特性存在一定差異，脫冰率越高，脫冰跳躍越嚴重。