用尖點突變理論研究疲勞斷裂事故

（中國電子科技集團公司第七研究所，廣東廣州 510310）

1 機械疲勞斷裂過程

疲勞斷裂是一種常見的破壞現象，疲勞斷裂發生時有以下幾點特點：第一，疲勞斷裂前零件不產生明顯的變形，突然發生斷裂。第二，零件破壞時的工作應力遠低于材料的抗拉強度，甚至低于材料的屈服極限。第三，斷口從宏觀來看由兩個區域構成，即金屬顆粒細、光亮的帶有疲勞線的疲勞裂紋擴展區和金屬顆粒組大的瞬時斷裂區。

疲勞斷裂需要經過三個階段，即微裂紋產生階段、疲勞裂紋擴展階段、斷裂。這樣一個過程也可以理解為加載受力后，材料疲勞磨損程度慢慢增加（微裂紋產生階段）經過一個相對穩定的增加期后，機械疲勞磨損量開始出現加速增加（疲勞裂紋擴展階段），機械磨損量一次次的增加，當接近材料壽命時，以前載荷作用對材料強度影響的累積效果，加上最后一次對材料強度性能的加劇惡化超過材料固有的承受界限，機械系統將發生瞬時斷裂（突變）。發生突變時的損傷值也就是系統的臨界損傷量。疲勞的最終結果是瞬間斷裂，實際上該過程其實是一個逐漸失效的非線性變化過程，該過程可用突變理論解釋。為了更加系統地研究該過程，了解臨界損傷量的數值，本文以突變理論為基礎，對疲勞斷裂過程進行分析和研究。

2 突變理論及突變類型

1972年法國數學家雷內·托姆在《結構穩定性和形態發生學》一書中明確地闡明了突變理論。突變理論研究的是從一種穩定組態躍遷到另一種穩定組態的現象和規律。它指出自然界或人類社會中任何一種運動狀態都有穩定態和非穩定態之分。在微小的偶然擾動因素作用下，仍然能夠保持原來狀態的是穩定態，而一旦受到微擾就迅速離開原來狀態的則是非穩定態，穩定態與非穩定態相互交錯。它提供了一種研究有躍進、不連續和突然質變的數學方法，突變理論涉及拓撲學、分叉理論、起點理論等許多理論，但是它以兩點為假設前提[1]：

（1）假定系統在任何時候的狀態可以由給定的n個變量系統受到m個（u1，u2，…um）獨立變量的控制，即這些變量的值決定了xi的值，并把xi叫做狀態變量，ui叫做控制變量。（2）系統的動力學可以由一個光滑的勢導出。

突變理論告訴我們，突變類型的數目不取決于狀態變量的數目，當控制參數不大于4個時，只有7種不同類型的突變，如表1所示。

表1 突變類型

3 疲勞斷裂事故的突變過程及特性

如圖1所示，建立疲勞斷裂突變模型，該模型具有折疊翼的平面曲線，由2個控制變量m、n（平面坐標，m和n分別表示工作應力和材料動力學特性）和狀態變量x（x表示裂紋長度，垂直坐標）構成的三維系統，模型分為上、中、下三葉，下葉和上葉都是穩定結構，分別表示了疲勞斷裂發生前和發生后的兩種穩定結構，中間葉是不穩定的失穩突變，疲勞斷裂過程可以描述為：系統從B點出發沿軌跡向A點逐漸演化，當接近折疊翼邊緣時，只要系統狀態量x有微小變化，系統陡然間從下葉突躍到上葉，在實踐中表現為當接近材料壽命時，以前載荷對材料強度影響累積，加上最后一次對材料強度性能的加劇惡化造成了斷裂表面瞬時增加，而材料的剩余界面很少，無法承受外加載荷而發生斷裂失穩。這一過程表現出了明顯的突變特點：

（1）多模態特征，即上下兩葉機械系統狀態不同；（2）突變特征，即經過折疊曲線時發生突變，瞬間斷裂；（3）發散特征，即系統狀態量x有微小變化導致狀態完全不同；（4）不可達特征，即實際上系統不可能達到中間狀態。

圖1 疲勞斷裂突變模型

4 機械疲勞斷裂事故發生的充分必要判據和條件

尖點突變的勢函數為：

由疲勞斷裂突變模型知，系統是由狀態變量x和2個控制變量構成的三維系統，其曲面平衡方程為：

把平滑函數的位勢導數為0的點稱之為定態點，而在某些定態點附近連續變化引起不連續變化的結果，將這些退化的定態點稱為奇點，故奇點集需要滿足：

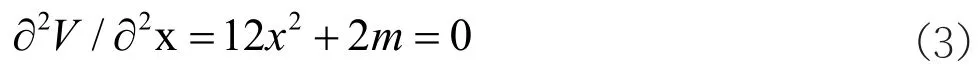
公式（2）和（3）聯立后消去x可以得到疲勞斷裂分叉集方程為：

公式（4）就是疲勞斷裂事故發生的充分必要判據，可以作為疲勞斷裂突變演化狀態與臨界失穩狀態的距離。隨著狀態量的不斷變化，當D=0時，狀態變量發生突變從而導致疲勞斷裂。

樊世清[2]等人對系統在疲勞斷裂過程中的變化情況作了深入研究，材料發生尖點突變的條件是試驗機主軸的剛度等于或小于試樣瞬時有效剛度與一個常數乘積的絕對值，即k≦|k＊e-2|,其中k是試驗機主軸的剛度，而在斷裂的臨界狀態時，由材料的原始特性和應力水平及疲勞損傷程度所決定。

5 機械疲勞斷裂過程的預防措施

機械疲勞的斷裂過程其實是一個非線性的變化過程，為了防止該類事故的發生關鍵在于能夠在微裂紋產生階段采取措施，防止疲勞區域的擴大，因為一旦擴大到疲勞裂紋擴展階段，將出現加速磨損的過程。為了降低應力集中應該在設計和加工階段階段做到如[3]：

（1）在設計階段。盡量避免尖角、缺口和截面突變，盡可能的平滑和均勻；盡可能地增大過渡處的圓角半徑；在不可避免要產生較大應力集中的結構處可采用減荷槽來降低應力集中的作用。（2）在加工階段。降低表面粗糙度，提高加工質量，提高疲勞極限；減少表面的氧化、裂紋、脫碳等表面缺陷。

6 結論

（1）機械疲勞的最終結果是瞬間斷裂，但是實際上該過程其實是一個逐漸失效的非線性的變化過程，該過程可用尖點突變理論解釋。（2）建立了機械疲勞斷裂突變模型，該模型是具有折疊翼的平面曲線，當接近折疊翼邊緣時，只要系統狀態量x（位移值）有微小變化，系統陡然間從下葉突躍到上葉，發生突變，斷裂發生。（3）隨著狀態量的不斷變化，當D=0時，狀態變量發生突變從而導致疲勞斷裂。機械疲勞斷裂分叉集方程為：結構和尺寸的突變是應力集中的機構根源，為了預防此類事故，關鍵是在微裂紋產生前采取措施，防止應力集中。