懸鏈斗卸船機臂架懸掛點的位置計算與優化

楊大海 崔益華 邵海林

南通潤邦重機有限公司

1 引言

懸鏈斗卸船機具有卸船效率高、清倉量小、綜合使用成本低等優勢，但是針對此種機型的設計資料較少，也不夠細化。實際項目中，臂架設計的懸掛吊點位置及臂架車輪安裝距的設計對整機至關重要，若設計不當會出現整機安全及使用性能不達標等問題。

2 懸鏈斗卸船機的特點及設計難點

2.1 懸鏈斗卸船機特點

懸鏈斗卸船機通過臂架上懸掛的自由懸垂鏈斗在船艙內進行取料，鏈斗機構將物料提升后卸載到臂架皮帶機上，再通過臂架皮帶機轉運到碼頭后方輸送系統，從而完成卸料。懸鏈斗機構安裝在可在臂架上來回移動的小車上，主臂架通過鋼絲繩與平衡配重相連而懸吊著，臂架的升降依靠俯仰鋼絲繩進行(見圖1)。臂架為三角形結構，根部上、下分別設有車輪組，沿門架海側門腿的內、外側移動[1-2]。整個臂架系統是一個自由狀態，由于小車在臂架橫梁上運行，根部車輪承載隨小車位置變化而變化，繼而影響整個門架的受力狀態。

圖1 整機設備圖

2.2 設計難點描述

總體設計中臂架的吊掛點位置至關重要。吊點靠前，臂架的平衡性不夠，當懸鏈機構在非工作極限位置時車輪會脫離軌道，存在安全隱患。吊點太靠后，工作時臂架的車輪輪壓會超過許用值。臂架的吊點及車輪安裝距的設計直接影響到臂架車輪的輪壓、臂架的穩定性、繼而影響臂架及門架結構的受力及剛性。

3 現有計算及問題分析

基本受力分析見圖2。針對臂架吊點位置的初選，常規的計算方法如下。

圖2 受力分析示意圖

要保證懸鏈處于海側極限位置時，車輪組輪壓不大于許用輪壓：

(1)

非工作懸鏈處于陸側極限位置時輪壓為正：

(2)

得出吊點的范圍為：L1min≤L1≤L1max。

式中，L為臂架吊點到門架中心的距離，m；∑M為懸鏈處于海側極限位置時，臂架上所有零部件的力矩和，Nm；∑G為懸鏈處于海側極限位置時，臂架上所有零部件的力矩和，Nm；∑M′為懸鏈處于陸側極限位置時，臂架上所有零部件的力矩和，Nm；∑G′為懸鏈處于陸側極限位置時，臂架上所有零部件的力矩和，Nm；G1，G2，G3，……Gi為懸鏈處于海側極限位置時，臂架上各部件的載荷，如臂架自重、鏈斗機構自重、皮帶機自重等，N；L1，L2，L3，……Li為懸鏈處于海側極限位置時，臂架上各部件的載荷選對門架中心對應的力臂，如臂架自重力臂、鏈斗機構自重力臂、皮帶機自重力臂等，m；G′1，G′2，G′3，……G′i為懸鏈處于海側極限位置時，臂架上各部件的載荷，如臂架自重、鏈斗機構自重、皮帶機自重等，N；[P]為車輪的許用輪壓，MPa；H為上下車輪的距離，m。

按以上步驟可以確定吊掛點的范圍，但是存在如下問題：

(1)計算所得值范圍較大，具體在哪一個位置是最優值無法得出，不能滿足實際工程應用中選取一個確切的點或一個較小的范圍值的要求。

(2)在實際項目中，還存在后方皮帶機的自重G和吊掛點的拉力F，這2個力對整個臂架的吊點位置選擇有很大影響。

(3)以式(1)、(2)計算出來的范圍可能會不存在，需要調整上下車輪組間距H的數值才能滿足實際工程需要，即H也是一個待優化的變量，需要探究L1與H之間的關系。

4 優化思路及方法

4.1 優化思路

針對以上問題，對此吊點的確定給出一個臂架優化的解決方案，為后續的實際項目提供指導和借鑒。

實際項目中，鏈斗機構的兩個極限位置是根據船型確定的，最大輪壓則是根據門架結構受力確定的。在這個系統中，臂架上下車輪組安裝間距H及臂架吊點位置L1是可調整的。所以優化思路為：以H、L1兩個變量建立優化函數。

4.2 計算方法

以臂架根部上車輪組為鉸點建立力矩平衡，以小車在臂架橫梁上兩個極限位置為計算工況，計算過程如下。

懸鏈處于海側極限位置時，移動臂架系統受力分析見圖3。

圖3 海側極限位置受力分析圖

TL1+4PH=GbLb+GmsLms

+GcsLcs+GiLi+GmiLi-GmlLml

-GclLcl+FLf

(3)

式中，P為工作最大輪壓，KN；Gi為鏈斗及運行小車機構重力，t；Gb為懸臂梁桁架金屬結構重量，t；Gms為海側皮帶機物料重量，t；Gcs為海側皮帶機及機架重量，t；Gmi為鏈斗中物料的重力，t；Gml為陸側皮帶機物料重量，t；Gcl為陸側皮帶機及機架重量，t；F為吊掛點的拉力，kN。

非工作懸鏈處于陸側極限位置，移動臂架系統受力分析見圖4。

圖4 陸側極限位置受力分析圖

(4)

式中，P′為非工作最小輪壓；Gms′=0，Gml′=0，Gmi′=0，則：

(5)

以上為兩個工況下的力學平衡式，由于其活動載荷一定，現用式(3)減去式(5)，去除無關因素，從而得出與自身結構相關的關鍵因素：

(T-T′)L1+(4P-4P′)H

=GmsLms-GmlLml+Gi(Li-L′)+GmiLi+(F-F′)Lf

(6)

式中，(F-F′)僅是物料變化引起，即

F-F′=0.5Gml/cosv

(7)

式中，(T-T′)為取料及輸送系統上物料變化引起的載荷，即

T-T′=Gms+Gml/2+Gmi

(8)

令GmsLms-GmlLml+Gi(Li-L′i)+GmiLi+(F-F′)Lf=K，整理后得：

(9)

極限狀態下，最大輪壓為許用輪壓，最小輪壓為零，則得出吊點與車輪安裝距的優化關系式如下：

(10)

L1為臂架吊點X方向水平距離，H為上下車輪組Y方向垂直間距，L1與X的關系見圖5。

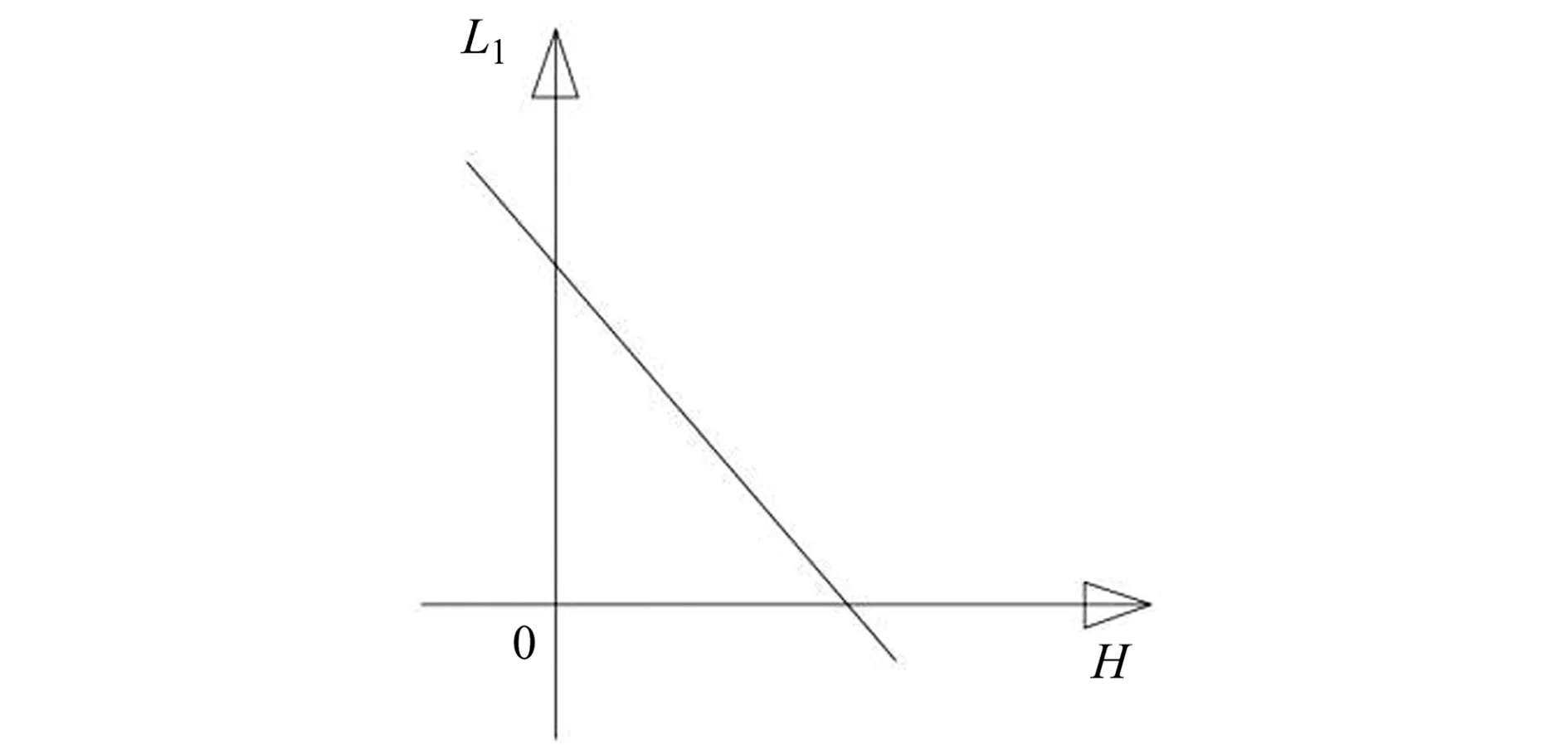
圖5 L1與H的關系圖

4.3 設置邊界條件

實際工程設計中，臂架吊點位置L1一定大于小車在陸側極限位置L′i，小于小車在海側極限位置Li的一半，即：L′i≤L1≤Li/2。在此范圍內優化確定H值，從而得出確切的L1值的大小。

4.4 最終驗證

通過以上得出吊點位置L1，臂架根部車輪安裝距H，從而確定整個臂架的總體結構尺寸，在此基礎上再確定門架的尺寸。整機布置確定后進一步驗算各工況下車輪輪壓和臂架受力。

5 實際應用

現以我司設計制造的額定生產率為800 t/h的懸鏈斗卸船機為例進行分析計算，基本參數見表1。

表1 基本參數

根據式(1)和式(2)，實際設計H為11.23 m時，計算出L1≤10.21 m，L1≥11.7 m，計算出的L1范圍不存在。由于H為固定數值，無法得出想要的結果，必須將H設為變量，不斷嘗試改變H值的大小才能確定出滿足要求的L1的范圍。

根據按優化后式(10)的算法：設定工作最大輪壓P=[P]=35 t，非工作最小輪壓P′=0.1 t，得出：L1=237-17.78H。根據實際情況，L1的大體范圍為L′i≤L1≤Li/2，從而計算出12.5≤H≤13。實際項目中，取H=12.5 m，L1=14.75 m。最后校核輪壓及整機穩定性，滿足使用要求。

6 結語

針對現有懸鏈斗卸船機臂架吊點位置設計計算出現的問題，通過對懸鏈斗卸船機兩個典型工況的受力分析，創新性的提出了臂架吊點及車輪安裝距兩個變量的優化計算方法，提高了設計的效率和準確性。同時，臂架的結構形式能夠快速準確的確定，進而優化了整機的布置，對此種機型的后續優化設計具有參考和借鑒意義。