不同權力結構下制造商雙渠道供應鏈的博弈分析
孫自來,王旭坪,詹紅鑫,阮俊虎
(1. 西北農林科技大學經濟管理學院,陜西 楊凌 712100;2. 大連理工大學系統工程研究所,遼寧 大連 116023)
1 引言
電子商務和移動電子商務時代,線下傳統批發銷售與線上直銷構成的雙渠道供應鏈逐漸成為制造商主要的運營模式[1-2]。國外如戴爾、蘋果、雅思蘭黛、耐克等品牌制造商[3],國內如華為、小米、海爾、李寧等品牌制造商[4]均采用線下傳統批發銷售渠道和線上直銷渠道相結合的雙渠道模式來銷售產品。
然而,品牌制造商線上直銷渠道的開辟,在增加其收益的同時[5-7],也不可避免的會與傳統批發零售渠道產生沖突[8]。這是因為直銷渠道的增設會使部分傳統零售渠道需求轉移到線上直銷渠道從而影響零售商的收益,進而可能影響制造商的收益,甚至供應鏈的總收益。尤其面對強大的零售商(比如沃爾瑪、國美等)時,品牌制造商在供應鏈中沒有顯著的競爭優勢,即:制造商在與零售商討價還價中沒有定價(包括批發價格和線上渠道零售價格)的主動權,此情景下,品牌制造商該制定怎樣的定價策略?進而當制造商在雙渠道供應鏈中擁有顯著優勢時或者制造商和零售商競爭優勢均衡時,這些情景又將對制造商雙渠道供應鏈運營帶來什么樣的影響?這就引出了本文擬探討的科學問題,即:供應鏈中不同權力結構將對制造商雙渠道供應鏈成員的定價、需求及收益產生怎樣的影響?這里需要說明的是,同文獻[9]一樣,本文中所指的制造商雙渠道供應鏈是指制造商線下傳統批發銷售渠道和線上直銷渠道構成的雙渠道供應鏈,是相對于文獻[29]中所提出的零售商雙渠道供應鏈來說的。
依據本文擬探討的科學問題和文獻[10],假設在單個擁有線下傳統批發及線上直銷雙渠道的制造商和單個線下零售商組成的供應鏈中存在三種權力結構,即制造商占優的Stackelberg博弈(權力結構1),零售商占優的Stackelberg博弈(權力結構2),制造商和零售商權力均衡的Nash博弈(權力結構3)。進一步,通過比較渠道間交叉價格彈性系數為0時和不為0時三種權力結構下制造商雙渠道供應鏈成員定價、需求及收益的大小來探討不同權力結構對各成員定價、需求及收益的影響。目前,運營及運作管理學者對雙渠道供應鏈及不同權力結構對雙渠道供應鏈運營管理影響方面的研究主要集中在以下三個方面:
1)直銷渠道的引入對分銷渠道的影響方面。Chiang等[1]分析了制造商開設網上直銷渠道對其傳統批發銷售渠道產生的影響,指出直銷渠道的開設是其提高傳統零售渠道效率的一個策略,可以促使零售商降低零售價格,即使直銷渠道的需求為零,制造商和零售商仍可增加利潤。Tsay和Agrawal[11]、Cattani等[12]、Khouja等[13]研究表明制造商在傳統批發零售渠道的基礎上增開線上直銷渠道可增加收益。而Yoo和Lee[14]指出制造商線上直銷渠道的開辟有可能導致零售價格的增加和消費者福利的降低,甚至可能降低獨立零售商的收益。上述研究基于線上直銷渠道增設前后收益的大小探討了線上直銷渠道對制造商雙渠道供應鏈的影響。Hill等[15-19]把網上直銷渠道配送時間作為主要影響服務水平的因素并把其融入到模型構建中,分析了直銷渠道配送時間和顧客線上直銷渠道接受程度對制造商和零售商定價行為的影響。另外,Chen等[20]基于實體渠道和線上直銷渠道二者服務水平的差異,探討了制造商雙渠道決策問題。梁喜等[21]進一步探討了線上直銷、線上分銷及線上代銷等不同雙渠道結構下,制造商的定價決策與渠道選擇問題。
2)不同博弈權力結構對傳統供應鏈的影響方面。Gaski等[22]較早從權力來源、可行使的權力來源、權力、沖突和滿意度、績效及有效性等方面探討了供應鏈成員的權力來源及其影響。Choi[23]研究了兩個制造商與一個零售商之間的三種不同權力結構的非合作博弈,結果表明,在線性需求函數中,制造商最好采用獨家經銷商銷售模式,而零售商則有動機與多家制造商商進行交易;當制造商和零售商權力平衡時,所有的渠道成員以及消費者都會受益。Shi等[10]研究結果表明預期需求決定了企業能否從供應鏈權力占優中獲利,同時,制造商總是可以通過降低需求不確定而獲利。Gao等[24]通過建立集中式和分散式供應鏈在三種渠道權力結構下的博弈模型,對一個制造商和一個零售商組成的閉環供應鏈進行了探討,研究表明零售商的利潤總是隨著主導渠道的權力從制造商向零售商轉移而增加,同時,當回收努力的需求擴張效率較低時,制造商的利潤也隨之下降;閉環供應鏈的最優渠道權力結構隨回收努力的需求擴展效率變化而變化。
3)不同博弈權力結構對雙渠道供應鏈的影響方面。Cai等[25]從供應商Stackelberg、零售商Stackelberg和Nash博弈的角度探討了不同價格折扣合同和定價方案對制造商雙渠道供應鏈的影響,結果表明,簡單的價格折扣契約可以有效地提高供應商和零售商的績效;在沒有價格折扣合同的情況下,相對于不一致的定價,一致的定價可以在犧牲供應商利益的情況下,為供應商Stackelberg博弈中的零售商帶來更多的利潤。Lu Qihui和Liu Nan[26]分析了雙渠道供應鏈系統中存在的三種定價博弈模型:一致定價的Stackelberg博弈、差異定價的Stackelberg博弈和一致定價的Nash博弈。張國興等[27]以制造商批發價格為外生變量,探討了三種權力結構對制造商雙渠道供應鏈成員價格、需求及收益的影響。林杰等[28]探討了兩類Stackelberg博弈權力結構對閉環供應鏈成員定價和利潤的影響,研究表明第三方回收價、制造商直接渠道回收價及制造商間接回收價受權力結構和消費者對第三方回收價的敏感程度的雙重影響。以上研究是以制造商傳統批發零售和線上直銷雙渠道經營策略為背景,探討了雙渠道供應鏈的運營管理問題以及不同博弈權力結構對雙渠道供應鏈的影響。另外,Chen Xu等[29]以零售商線上線下雙渠道零售為背景,分析了不同博弈權力結構對零售商雙渠道供應鏈的影響。在文獻[29]的基礎上,王旭坪等[30]以跨境電商雙渠道零售供應鏈為背景,從顧客凈效用角度出發,構建渠道需求函數和收益函數,探討了不同權力結構對供應鏈成員定價、需求及收益的影響。
綜上,上述文獻大都以制造商傳統批發銷售加線上直銷所構成的雙渠道供應鏈為背景,探討雙渠道供應鏈的運營管理問題。較少有文獻從制造商的角度,以制造商傳統批發銷售加線上直銷所構成的雙渠道供應鏈為背景,來分析和研究不同權力結構對制造商雙渠道供應鏈中各成員定價,需求及收益的影響。雖然文獻[27]研究了類似的問題,但其文中假設制造商的批發價格是由長期合同決定的,為模型的外生變量,沒有探討不同權力結構對制造商批發價格的影響。然而,不同權力結構對供應鏈的影響首先是通過影響供應鏈成員的價格體現出來,進而影響需求,最后價格和需求共同決定了對收益的影響。另外,批發價格作為制造商與零售商討價還價的主要談判目標,尤其在制造商雙渠道銷售環境下,批發價格和線上直銷渠道零售價格均由制造商同時決策,其定價的高低很有可能受雙方權力地位的影響,進而影響傳統渠道零售商的定價決策。而如果把制造商批發價格作為模型的外生變量,不同權力結構對批發價格的影響將無法體現,進而對傳統渠道零售價格和線上直銷渠道價格的影響,甚至對傳統渠道需求和線上直銷渠道需求及供應鏈成員收益的影響也將不能充分體現。因此,基于以上分析,有必要將批發價格設定為模型的內生變量,來探討不同博弈權力結構對制造商雙渠道供應鏈成員定價、需求及收益的影響,同時有理由相信本文與文獻[27]主要結論的不一致是由于將批發價格由外生變量改內生變量所導致的。另外,渠道交叉價格彈性系數為0時和不為0時,三種博弈權利結構對制造商雙渠道供應鏈均衡解的影響所具有的魯棒性進一步驗證了本文所得結論的合理性。
2 問題描述與模型構建
本文主要探討在一個制造商和一個零售商組成的兩層供應鏈中,不同權力結構對制造商雙渠道供應鏈成員價格、需求及收益的影響。同文獻[27]一樣,假設制造商的生產成本為0,批發價格為w。制造商采用線下傳統批發渠道和線上直銷渠道雙渠道模式來銷售產品,在線下傳統批發渠道中,制造商以批發價格w把產品銷售給零售商,然后零售商以單位零售價pt銷售給顧客,假設零售商單位銷售成本為0;在線上直銷渠道中,制造商以零售價pd把商品直接銷售給顧客,同樣假設制造商直銷渠道單位銷售成本為0。另外,為保證制造商雙渠道模式的存在,即保證傳統渠道批發機制成立,需w 和文獻[27]相同,假設產品需求和價格呈線性關系,構建如下的需求函數: 傳統批發渠道需求函數: Dt=θa-pt+bpd (1) 線上直銷渠道需求函數: Dt=(1-θ)a-pd+bpt (2) 其中,下標t代表線下傳統批發零售渠道,下標d代表制造商線上直銷渠道;Dt代表線下傳統批發零售渠道的市場需求,Dd代表制造商線上直銷渠道的市場需求;pt和pd分別代表線下傳統批發零售渠道零售價格和線上直銷渠道價格。a代表產品潛在市場規模;θ代表線下傳統批發零售渠道市場份額,1-θ代表線上直銷渠道市場份額;b為渠道交叉價格彈性系數,且0≤b<1,即本渠道價格對需求的影響大于其他渠道價格對本渠道需求的影響。 另外,假設制造商和零售商在需求和成本信息方面是對稱的,制造商和零售商都是理性的,各自追求自身收益的最大化。具體模型如下圖1所示: 圖1 制造商雙渠道銷售模型示意圖 制造商為主導的Stackelberg博弈模型中,制造商處于領導者地位,零售商處于跟隨者地位。決策順序為,制造商首先確定批發價格和線上直銷渠道零售價格,然后零售商根據制造商確定的批發價格和線上直銷渠道零售價格確定線下傳統渠道的零售價格。在該競爭模型中,制造商和零售傳統商的收益可分別表示為: πm(w,pd)=wDt+pdDd (3) πr(pt)=(pt-w)Dt (4) 把式(1)和式(2)代入式(3)和式(4)后得: πm(w,pd)=w(θa-pt+bpd)+ pd[(1-θ)a-pd+bpt] (5) πr(pt)=(pt-w)(θa-pt+bpd) (6) 根據博弈論逆序求解過程,零售商已知制造商的批發價格w和直銷渠道零售價格pd,其按照自身收益最大化原則決定其傳統渠道零售價格pt。對公式(6)求關于pt的一階導數并令其等于零解得 (7) 制造商根據自身收益最大化決定批發價格w和直銷渠道零售價格pd,分別對w和pd求一階導數并令其等于零解得 (8) (9) (10) (11) 因此,制造商占優的Stackelberg博弈模型中,供應鏈的總收益為: (12) 零售商占優的 Stackelberg 博弈模型中,零售商處于領導者地位,制造商處于跟隨者地位。決策順序為,零售商首先確定傳統渠道零售價格,然后制造商根據零售商確定的傳統渠道零售價格確定其批發價格和直銷渠道零售價格。 假設傳統渠道的單位收益為mt=pt-w[10,29],據此,制造商的收益可表示為: πm(w,pd)=w(θa-pt+bpd) +pd[(1-θ)a-pd+bpt] =w(θa-mt-w+bpd) +pd[(1-θ)a-pd+b(mt+w)] (13) 零售商收益可表示為: πr(pt)=(pt-w)(θa-pt+bpd) (14) 根據博弈論逆序求解過程,制造商已知零售商在傳統渠道的零售價格pt,其會按照自身收益最大化原則決定其直銷渠道零售價格pd和批發價格w。對公式(13)求關于pd和w的一階導數并令其等于零解得 πr(pt)=(pt-w)(θa-pt+bpd) (15) 零售商根據自身收益最大化決定傳統渠道零售價格pt,對pt求一階導數并令其等于零解得 (16) (17) (18) (19) 因此,零售商占優的Stackelberg博弈模型中,供應鏈的總收益為: (20) 在Nash博弈模型中,供應鏈成員同時做出決策。制造商假定零售商在傳統渠道的零售價格已定來確定自己直銷渠道價格和批發價格;與此同時,零售商假定制造商直銷渠道價格和批發價格已定來確定傳統渠道零售價格。 假設傳統渠道的單位收益為mt=pt-w[10,29],據此,制造商的收益可表示為: πm(w,pd)=w(θa-pt+bpd) +pd[(1-θ)a-pd+bpt] =w(θa-mt-w+bpd) +pd[(1-θ)a-pd+b(mt+w)] (21) 零售商收益可表示為: πr(pt)=(pt-w)(θa-pt+bpd) (22) 根據收益最大化原則,對公式(21)求關于pd和w的一階導數并令其等于零解得 同時,對公式(22)求關于pt的一階導數并令其等于零解得 據此可得 (23) (24) (25) (26) 因此,權力平衡的Nash博弈模型中,供應鏈的總收益為: (27) (1)首先對比分析當渠道交叉價格彈性系數b=0時,不同博弈權力結構對供應鏈成員價格、需求及收益的影響。 命題1制造商雙渠道銷售模式下,在制造商為主導的和零售商為主導的 Stackelberg博弈中,傳統渠道零售價格相等,同時大于Nash博弈中的傳統渠道零售價格;同樣在兩類Stackelberg博弈中,傳統渠道需求相等,但均小于Nash博弈中的傳統渠道需求。即 由命題1可知,即使兩個渠道之間的需求轉移比例接近0時,制造商和零售商之間的Nash博弈權力結構仍會對傳統批發渠道零售價格決策和需求產生影響;而命題2表明:當兩個渠道之間的需求轉移比例接近0時,供應鏈成員之間的博弈策略不會對直銷渠道的價格和需求產生影響,當然也不會對顧客直銷渠道的購買行為造成影響;命題3表明:即使兩個渠道之間的需求轉移比例接近0時,制造商和零售商之間的博弈策略仍會對制造商的批發價格產生影響。 證明:由式(11),(19)和(26)可知 命題5制造商雙渠道銷售環境下,制造商在其為主導的Stackelberg博弈中的收益最大,Nash博弈中次之,零售商為主導的Stackelberg博弈中制造商的收益最小。 證明:把b=0代入第3節所求的制造商收益均衡解中,可得對應的制造商收益分別為: 命題6制造商雙渠道銷售環境下,兩類Stackelberg博弈中供應鏈總收益相等,Nash博弈中供應鏈總收益大于兩類Stackelberg博弈中供應鏈總收益。 依據命題命題4和命題5,可知即使兩個渠道的需求交叉價格彈性系數為0(即不存在渠道之間的需求轉移),供應鏈成員之間的博弈策略仍會對制造商(零售商)的收益產生影響;而命題6表明:當兩個渠道之間的需求轉移比例接近0時,兩類Stackelberg博弈不會對供應鏈的總收益產生影響,而Nash博弈會使供應鏈的總收益增加。 (2)本部分探討當渠道交叉價格彈性系數0 命題7表明,當渠道交叉價格彈性系數0 命題8制造商雙渠道銷售環境下,在制造商為主導的和零售商為主導的 Stackelberg博弈中,傳統渠道需求相等,且均小于Nash博弈中的傳統渠道需求;制造商直銷渠道需求在兩類Stackelberg博弈中相等,且均大于Nash博弈中的直銷渠道需求。即 由命題8可知,當渠道交叉價格彈性系數0 命題9制造商雙渠道銷售模式下,零售商在其為主導的Stackelberg博弈中收益最大,Nash博弈中次之,制造商為主導的Stackelberg博弈中零售商的收益最小;制造商在其為主導的Stackelberg博弈中的收益最大,Nash博弈中次之,零售商為主導的Stackelberg博弈中制造商的收益最小;兩類Stackelberg博弈中供應鏈總收益相等,且均小于Nash博弈中供應鏈總收益。即 依據命題9,可以得知,當渠道交叉價格彈性系數0 本文采用博弈分析的方法,探討了不同博弈權力結構對制造商雙渠道供應鏈的影響。結果表明:1)渠道交叉價格彈性系數為0時和不為0時,三種博弈權利結構對制造商雙渠道供應鏈均衡解的影響具有一定的魯棒性;2) 制造商雙渠道銷售模式下,Stackelberg博弈權力結構對傳統批發渠道零售價格沒有影響,但Nash博弈市場結構促使傳統渠道零售價格下降;三種博弈權力結構對制造商線上直銷渠道定價沒有影響,但對制造商批發價格決策有顯著影響,即批發價格隨其博弈主導地位下降而逐漸降低;3) 渠道交叉價格彈性系數不為0時,制造商O2O雙渠道銷售模式下,Stackelberg博弈權力結構對制造商線上直銷渠道需求和線下傳統批發零售渠道需求均沒有影響;而Nash博弈權力結構中,制造商線上直銷渠道需求降低,而線下傳統批發零售傳統渠道需求增加;4)制造商O2O雙渠道供應鏈中,供應鏈成員的權力地位與各自收益具有顯著的正相關關系,即制造商和零售商在制造商雙渠道供應鏈中占據主導者可獲取更多的收益;而供應鏈總收益在權力平衡的Nash博弈權力結構中最大。 本文的管理啟示是:首先從定價角度來看,制造商雙渠道銷售模式下,為平衡線下線上市場需求,制造商在三類博弈權力結構中不能隨意調整線上直銷渠道價格,而應保持定價的穩定性;零售商可以在權力平衡的Nash博弈中采取降價的策略以應對激烈的市場競爭;制造商也應隨其博弈主導地位的變化靈活調整其批發價格以應對激烈的市場競爭。其次從收益角度來看,制造商雙渠道銷售模式下,制造商在與零售商的博弈中,誰處于較有利的地位,誰將獲得較大的收益,因此,制造商和零售商都要力爭獲取和保持自己的競爭優勢;最后從整個供應鏈角度來看,供應鏈成員之間應保持適度的競爭,這樣不但可以提高整個供應鏈的總收益,而且可以使傳統線下渠道的顧客受益。另外,把顧客對傳統渠道和線上直銷渠道偏好的異質性融入到需求模型的構建中將是未來一個富有挑戰性也更有意義的研究方向。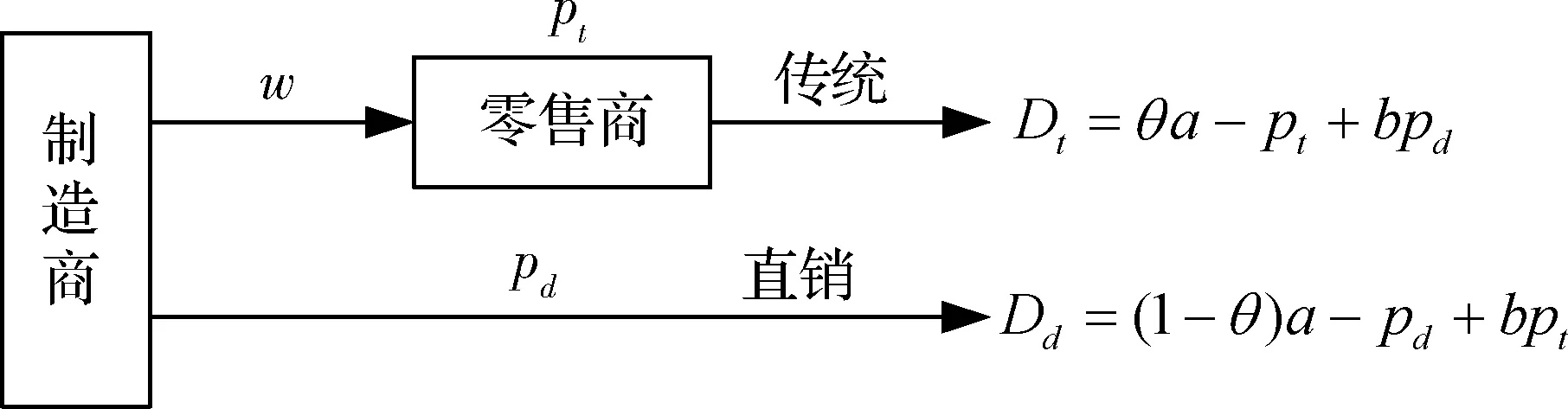
3 不同權力結構下制造商雙渠道供應鏈成員的定價與收益
3.1 制造商占優的Stackelberg博弈模型
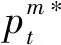
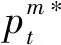
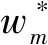
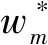


3.2 零售商占優的Stackelberg博弈模型
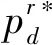
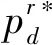
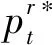
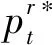
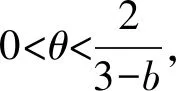
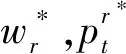
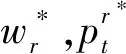
3.3 權力平衡的Nash博弈模型
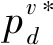
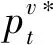
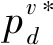
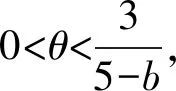
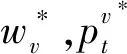
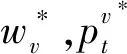
4 比較分析
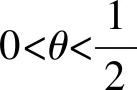
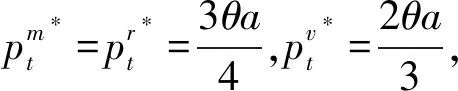
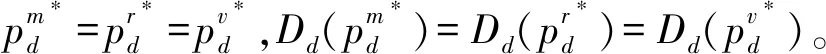
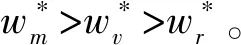
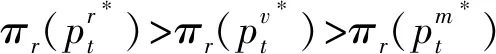
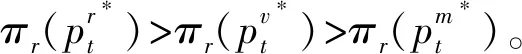
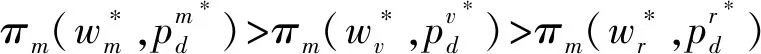
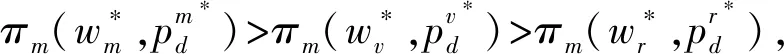
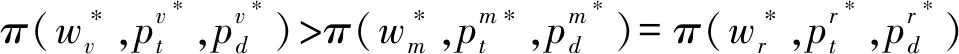
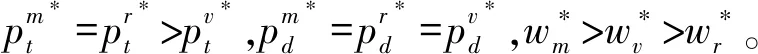
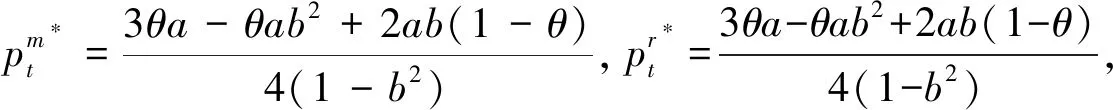
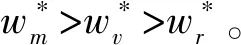

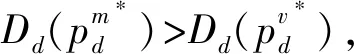
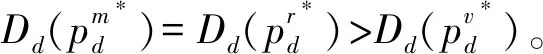
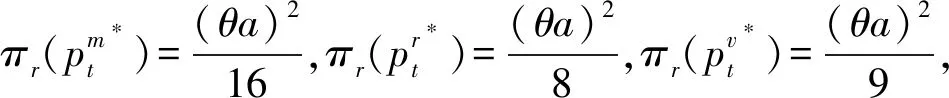
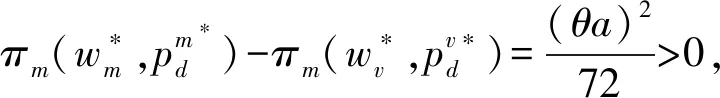
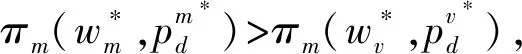
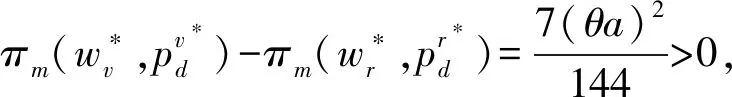
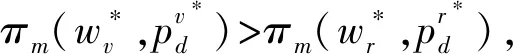
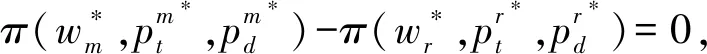
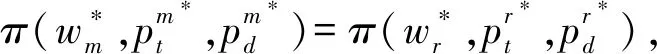
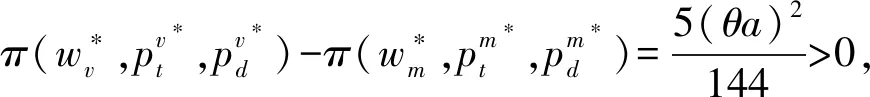
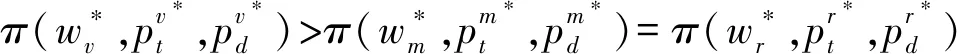
5 結語

