改進的廣義Kelvin巖石蠕變模型研究

王 游，盧小雨,2*，李亞倩

(1.安徽理工大學 土木建筑學院，安徽 淮南 232001；2.安徽理工大學 力學與光電物理學院，安徽 淮南 232001)

巖石蠕變是指巖石在應力、水、溫度等復雜條件下，巖石所呈現的與時間相關的某些力學特性，如彈性后效、松弛、破壞等，即時間效應[1]，它是巖石固有的屬性之一，影響著巖體結構的長期安全性和穩定性，建立能全面模擬巖石蠕變變形的蠕變模型一直是巖石蠕變學研究的熱點和難點。由于巖石本身的復雜性，其力學參數往往隨加載時間不斷變化，采用非線性的蠕變模型更能準確模擬巖石蠕變全過程[2]。目前建立巖石非線性蠕變模型的方法主要采用以下兩種：一是設計新的非線性元件代替線性元件,如陳家瑞[3]在三參量蠕變模型的基礎上引入非牛頓體，從而得到了非線性蠕變模型，該模型可以較好地模擬巖石在不同應力水平下的蠕變曲線；蘇騰等[4]基于分數階導數和連續介質損傷理論建立了非線性蠕變模型，該模型可以較好地模擬巖石在不同應力載荷下的蠕變形式且能反映巖石的力學性質在不同蠕變階段的變化情況。二是引入損傷力學理論和Lemaitre等效原理，將損傷因子引入蠕變方程中，進而建立蠕變損傷模型,如羅潤林等[5]基于巖石蠕變機理，引入硬化函數和損傷變量，建立了巖石非線性蠕變模型；劉新喜等[6]基于Kachanov損傷理論把損傷影響參數引入Maxwell模型，使其符合蠕變軟化階段的損傷特性；曹文貴等[7]引入損傷理論和Kachanov損傷演化規律，建立了一個可以充分反映巖石加速蠕變特性的模型；丁靖洋等[8]基于巖石加速蠕變過程中的力學特性，假定Abel黏壺的黏性系數損傷符合Weibull隨機分布，得到了鹽巖蠕變損傷模型，取得了較好的擬合結果；楊逾等[9]基于Lemaitre原理建立了非線性損傷Burgers模型，取得了較好的擬合結果；王春萍等[10]基于花崗巖高溫蠕變過程的損傷效應并考慮彈性模量和黏性系數隨溫度的變化關系，建立了高溫條件下的溫度損傷元件，該元件可以較好地模擬巖石加速蠕變變形。

綜上所述，盡管國內外許多學者在巖石蠕變模型方面取得了一些研究成果，但存在著以下幾個問題：首先，模型參數辨識不合理，有的學者直接用一維蠕變方程去擬合常規三軸蠕變實驗，雖然可以取得較好的擬合結果，但模型參數在一維和三維應力情況下物理含義并不相同；其次，巖石蠕變參數與時間成函數關系，把損傷因子引入線性元件后，采用微分方程的形式求解蠕變方程存在一定的困難，增加了蠕變方程的描述難度，這也是現階段蠕變模型存在的主要問題，并且有的學者直接把有效參數引入元件組合模型中，這導致有的模型在數學上并不嚴謹；最后，目前大多數蠕變模型以巖石長期強度為依據來改進和組合進而建立能模擬巖石加速蠕變的模型，而以加載時間為依據而建立的模型較少[11]。因此在蠕變模型已有研究成果的基礎上，考慮巖石彈性模量衰減規律和引進一種帶時間觸發的非線性黏性體，將之與廣義Kelvin模型進行組合，得到了一個能夠全面模擬巖石蠕變變形的非線性蠕變模型，該模型描述較為簡單，克服了傳統模型不能全面模擬巖石蠕變變形的不足，且不需要知道巖石的長期強度，引入相關蠕變試驗數據驗證蠕變模型的合理性和適用性，并對模型參數進行敏感性分析，研究成果可為今后開展類似研究提供一定的參考價值。

1 非線性蠕變模型的建立

廣義Kelvin模型由一個彈性元件與一個黏性體并聯后再與一個彈性元件串聯組成。模型如圖1所示:

廣義Kelvin模型的蠕變方程可表示為:

(1)

式中，ε為蠕變量；E0為彈性體彈性模量；η1為Kelvin體黏性系數；E1為Kelvin體彈性模量；σ0加載應力。

廣義Kelvin模型難以模擬巖石加速蠕變變形，同時模型的黏彈性參數并不是定常數，而是隨加載時間不斷變化的參數。張樹光等[12-13]研究表明巖石彈性模量隨加載時間不斷減少，因此假定廣義Kelvin模型中彈性體彈性模量符合下式:

E(t)=a+bexp(-ct)

(2)

式中，a、b、c為無量綱參數。

當σ=σ0時，彈性體一維蠕變方程為:

(3)

巖石蠕變可以分為衰減蠕變，等速蠕變和加速蠕變三個階段，而每個階段對應不同的起始時間，由于時間具有不可逆性，故引入一個帶時間觸發的非線性黏性元件來模擬巖石的加速蠕變變形。非線性黏性元件模型如圖2所示。

該元件滿足以下應力-應變關系:

(4)

式中，tF為巖石加速蠕變起始時間；λ蠕變參數；ηa非線性黏性元件黏性系數；tF確定方法見文獻[14]。

將非線性黏性元件與廣義Kelvin模型進行組合，從而得到新的非線性蠕變模型。模型如圖3所示:

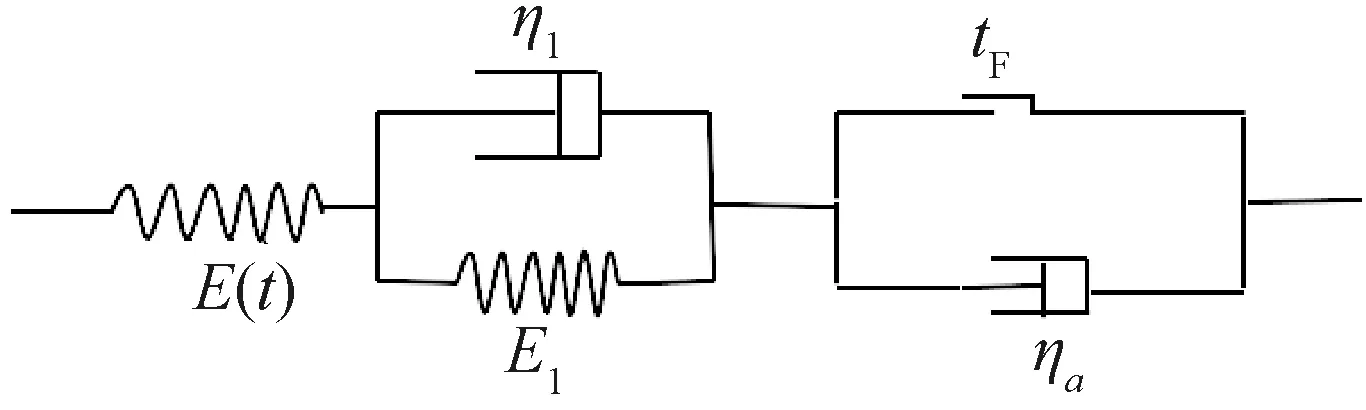
圖3 非線性蠕變模型Fig.3 Nonlinear creep model

在t=0時，對模型施加恒定應力σ0，則有

(1)對于彈性體E(t)，其本構方程為:

σ0=E(t)ε0=(a+bexp(-ct))ε0

(5)

式中，E(t)為式(2)表達式，ε0為彈性體應變。

(2)對于Kelvin體，其本構方程為:

(6)

對式(6)進行變換求積分，并考慮初始條件：t=0,ε1=0，則有

(7)

式中，ε1為Kelvin體應變。

(3)對于非線性黏性元件，其本構方程為:

(8)

式中，ε2為非線性黏性體應變。

由于應變可以疊加，則根據式(5)、(7)、(8)，可得巖石在一維應力狀態下非線性蠕變方程為:

(9)

(10)

式(9)可模擬巖石衰減蠕變變形和等速蠕變變形，式(10)可模擬巖石蠕變全過程。

將一維蠕變模型推廣到三維應力狀態下，更符合巖石實際受力狀態，具有更高的參考價值。在三維應力狀態下，巖石內部張量σij可分解為球應力張量σm和偏應力張量Sij，同樣巖石應變張量εij由球應變張量εm和偏應變張量eij組成[15]，并且在彈性狀態滿足：

(11)

式中，K為體積模量；G為剪切模量；E為彈性模量；μ為泊松比，可認為不變。

由廣義塑性力學可知，巖石類材料中的塑性應變問題應采用相關聯流動法則來解決，對于常規三軸蠕變實驗，一般認為球應力張量對巖石蠕變影響很小，偏應力張量在巖石蠕變中起主要作用，因此屈服函數可采用Mises函數，因此三維蠕變方程可表示為：

(12)

(13)

式中，G1為彈性體剪切模量，其余參數與上文一致。

2 參數辨識及敏感性分析

2.1 參數辨識和模型驗證

將蠕變實驗數據代入巖石蠕變模型中進行曲線擬合和參數反演是蠕變研究中常用的方法，1stOpt軟件憑借其超強收斂速度和不受初始賦值的影響，通過其獨特的全局優化算法，在大多數情況下都能取得較好的結果[16]。為驗證新的巖石蠕變模型的正確性和適用性，擬合了白堊系凍結軟巖蠕變試驗數據[17]和天然頁巖蠕變試驗數據[18]。擬合結果分別如圖4、圖5所示,參數反演結果見表1、表2。

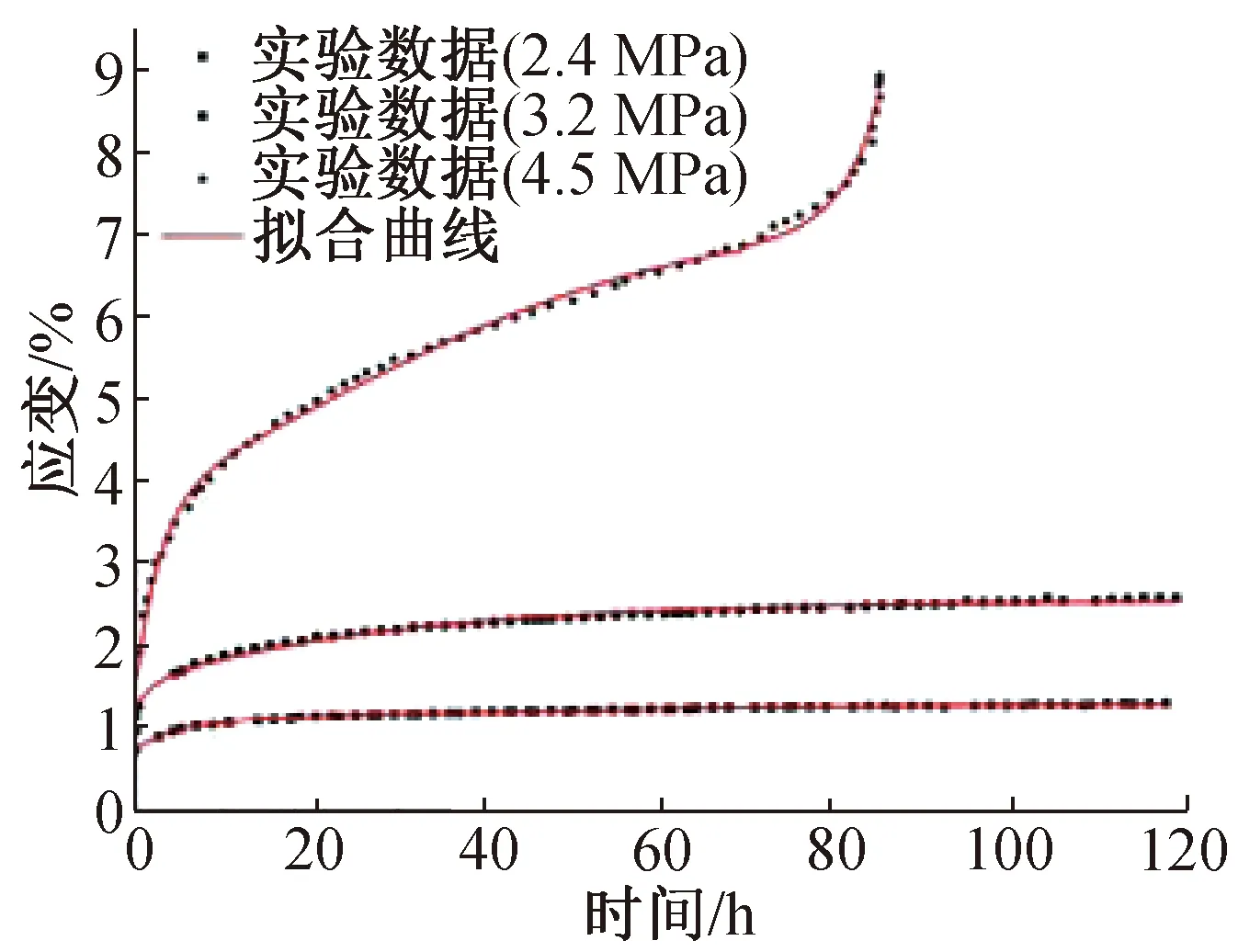
圖4 軟巖非線性蠕變模型與實驗結果對比Fig.4 Comparison of soft rock nonlinear creep model and experimental results

表1 軟巖非線性蠕變模型參數

表2 頁巖非線性蠕變模型參數

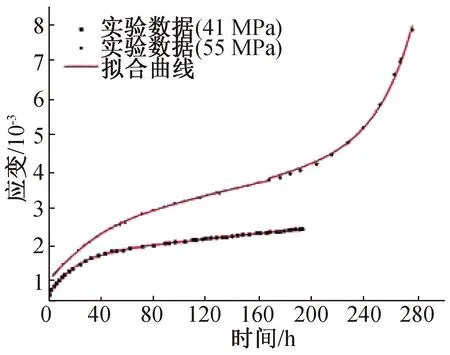
圖5 頁巖非線性蠕變模型與實驗結果對比Fig.5 Comparison of shale nonlinear creep model and experimental results

從圖4、圖5對比情況來看，本文建立的非線性蠕變模型與實驗數據吻合程度較好(尤其是加速蠕變階段)，模型能夠模擬巖石各個階段蠕變曲線，同時也驗證本文建立的非線性蠕變模型對軟硬巖及不同加載應力水平下都具有較好的適用性。

引入綠片巖[19]和紅砂巖[20]的三軸壓縮蠕變實驗數據進一步驗證該模型對巖石加速蠕變變形模擬的準確性和適用性。為了擬合實驗數據方便，將三維蠕變方程進行系數簡化，簡化結果如式(14)所示，擬合結果分別如圖6、圖7所示，擬合參數見表3。

表3 加速蠕變模擬參數

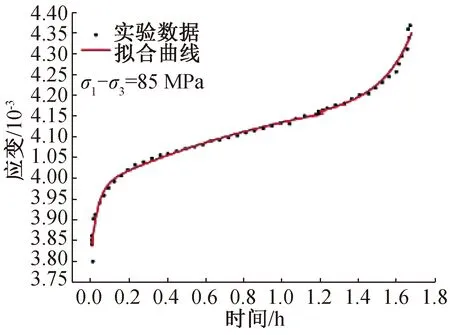
圖6 綠片巖非線性蠕變模型與實驗結果對比Fig.6 Comparison of greenschist nonlinear creep model and experimental results

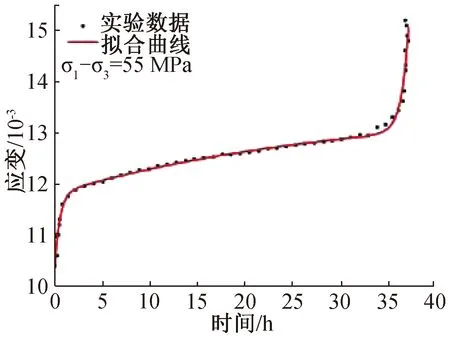
圖7 紅砂巖非線性蠕變模型與實驗結果對比Fig.7 Comparison of red sandstone nonlinear creep model and experimental results

a2exp(t-tF)λ

(14)

從擬合結果與實驗數據對比情況來看，再次說明該模型對不同蠕變破壞時間下的加速蠕變變形都能夠較好地模擬。

2.2 參數λ對蠕變全過程曲線影響分析

參數a、b、c表示巖石彈性模量隨加載時間的變化關系，已有許多學者對此進行分析[21]，在此并不詳述。巖石加速蠕變特性是影響地下工程穩定性和安全性的主要力學特性，在此給出參數λ對巖石蠕變全過程曲線的影響。結果如圖8所示。

圖8分析了蠕變參數λ對巖石蠕變全過程曲線的影響，圖中給出了蠕變參數λ為0.025、0.036 75、0.050、0.070時蠕變曲線的對比(其余參數見表2，加載應力為55 MPa)。由圖8可知，保持模型中其他參數不變，巖石加速蠕變變形和蠕變速率隨參數λ的增大而呈現非線性增大，巖石更快地進入加速蠕變階段，根據λ取值的不同，該模型可以模擬不同巖性及不同應力水平下的加速蠕變變形。

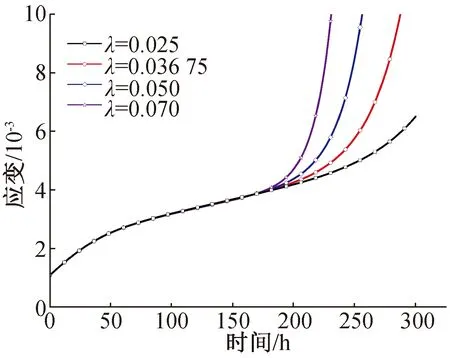
圖8 蠕變參數λ變化對全程蠕變曲線的影響Fig.8 The impact of creep parametersλchanges on the whole-process creep curve

3 結論

1)在廣義Kelvin模型的基礎上串聯一個帶時間觸發的非線性黏性體，同時考慮巖石彈性模量隨加載時間的衰減規律，從而建立了新的非線性蠕變模型，并給出了模型的一維和三維蠕變方程。

2)引入相關蠕變實驗數據對非線性蠕變模型的合理性和可行性進行驗證并同時反演得到模型參數，結果表明該模型可以準確模擬各類巖石的非線性蠕變曲線(尤其是加速蠕變階段)，克服了傳統經典模型的不足。

3)對模型蠕變參數λ進行了分析，結果表明隨著參數λ的增加，巖石加速蠕變速率也增大，巖石更快地進入加速蠕變階段，也說明巖石加載時間是導致巖石蠕變破壞的一個十分重要的因素。