混流式水輪機上冠空腔結構內部流場及單向流固耦合分析

梁武科，黃漢維，吳子娟，董 瑋，嚴 欣，劉云琦

（1.西安理工大學 水利水電學院，陜西 西安 710048；2.西北農林科技大學 水利與建筑工程學院，陜西 楊凌 712100）

1 研究背景

混流式水輪機在運行時，水流作用在水輪機轉輪上軸線方向上的分力稱為軸向力，主要包括轉輪葉片、上冠和下環內外表面受到的軸向力，由轉輪上冠處的軸向力過大而引起推力軸承的燒瓦事故在很多電站出現過[1]，這樣的事故不僅為機組的安全穩定運行帶來了極大的威脅，而且為電站的正常經營帶來了經濟損失和社會損失，為避免事故的發生則要減小轉輪上冠間隙流道的軸向力，解決的方法通常是在上冠處開設減壓孔和空腔，以排出上冠背面的間隙滲漏水[2]，降低上冠背面的水壓，這是減小轉輪軸向力和改善主軸密封工作條件的一個重要措施。國內外混流式水輪機泄水降壓結構較多，不同型號水輪機的上冠間隙流量的排出方式各不相同，上冠內部設置空腔結構是大中型水輪機主要的排水方式之一[3]，但是目前對此種排水結構的研究較少。

國內外有很多關于水輪機的間隙流動的研究[4-6]，研究內容主要集中在轉輪間隙內流動分析、間隙泄露量的計算方法和間隙對水輪機性能的影響因素等方面，文獻[7]研究了主流道內速度和壓力分布以及空腔、泄水孔和密封間隙內的流動特征，發現空腔上頂面壓力隨著間隙寬度的增加先降低然后又回升，而泄漏流量隨間隙寬度的增大而增加。文獻[8]對含減壓管的原型水輪機進行三維全流道湍流計算，認為減壓管的存在，會在轉輪上冠和頂蓋之間的壓力腔中產生小的高壓區，并且轉輪密封間隙進口壓力隨著密封間隙泄漏量的增大而減小。文獻[9]針對含有轉輪間隙的混流式水輪機的圓盤效率損失進行了計算，發現考慮間隙流動會對水輪機效率預測的精度產生影響，且轉輪下環表面造成的效率損失遠高于上冠表面。文獻[10]為了分析下環間隙對混流式水輪機能量特性和內部流態的影響，對4種流量工況下、5種下環間隙的混流式水輪機模型機進行三維全流道數值計算，揭示了不同工況時下環間隙與水輪機性能的關系。文獻[11]認為簡化水力機械中的間隙結構會影響數值結果，其研究人員在瞬態條件下對高水頭混流式水輪機進行數值模擬時，考慮了與密封間隙有關的所有幾何細節，發現在考慮密封間隙時，混流式水輪機在無葉片區和尾水管的壓力波動與試驗數據更接近，且在水輪機甩負荷過程中，考慮密封間隙的數值模擬可以更精確的反映出轉輪所受的水推力。

轉輪葉片流固耦合計算的研究也受到關注，文獻[12]采用流體動力學技術，基于瞬態流固耦合對轉輪葉片進行了動應力分析，發現在低負荷下葉片動應力最大，又對轉輪單個葉片進行了模態分析，排除了發生水力共振的可能。文獻[13]提出了一種新的界面模型用于流固耦合計算中的載荷傳遞，該模型包括流場載荷輸出、載荷轉換和固體場載荷自動施加三部分，驗證后表明載荷轉換誤差在1%以內。文獻[14]提出了一種流場與結構場網格節點一一對應的耦合界面模型，保證了流固耦合界面上水壓力由流體場向結構場的精確傳遞，同時又使耦合計算的效率提高。

本文研究的水輪機的上冠間隙流域，是通過間隙入口流入頂蓋與上冠之間的空腔，再經減壓孔流出，最后流入上冠內的空腔，由泄水錐排出。利用CFD 模擬水輪機的間隙流動的技術已較為成熟[15-17]，采用CFD 以含有上冠間隙、減壓孔及上冠空腔的水輪機作為研究對象，對全流道流體域進行計算，再與轉輪固體域進行單向瞬態流固耦合，探討上冠空腔及減壓孔等裝置，對水輪機內部流態及轉輪瞬態結構力學特性和振動特性的影響，為混流式水輪機密封間隙流排出方式的設計，提供一定的參考，也為水輪機的改造與優化提供一些方向。

2 計算方法

2.1 計算區域和網格劃分本文研究的對象為混流式水輪機模型機，表1為水輪機模型機的主要相關參數。圖1為該混流式水輪機的全流道幾何模型。圖2為UCCS的水輪機轉輪剖面圖，各部件幾何模型由三維造型軟件UG 完成。

表1 水輪機模型主要參數

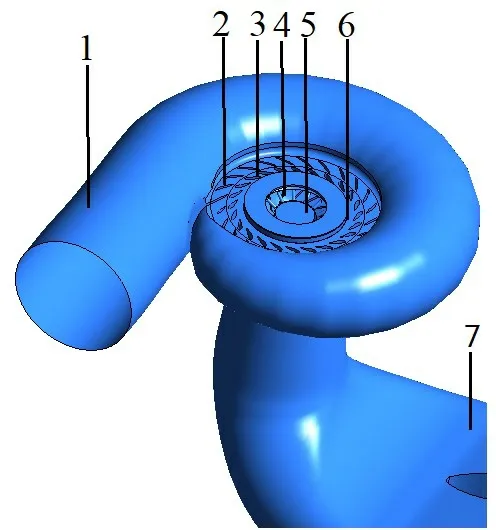
圖1 全流道計算模型

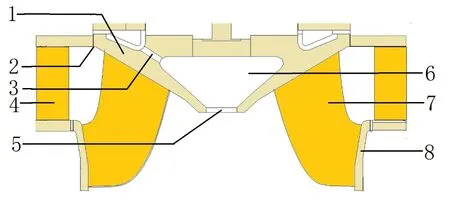
圖2 UCCS的水輪機轉輪剖面

對蝸殼、固定導葉、活動導葉、轉輪、尾水管、密封間隙、上冠空腔和減壓孔均采用了六面體結構化網格進行劃分，各部分交界面網格匹配度達到1∶1.5 以內，因上冠間隙域網格尺寸較小，上冠間隙入口處附近的主流域為活動導葉域，而活動導葉域網格尺寸較大，為了減小因為網格突變而引起的計算誤差[7]，活動導葉與間隙入口的交界面附近網格采用逐漸緩慢過渡，網格尺寸漸漸由大到小的劃分形式，圖3為間隙流道附近活動導葉的網格。

采用理查德森外推法進行網格無關性驗證，設置3 組不同網格數（348×104，460×104，600×104）的網格方案，關注水輪機的效率與水頭隨網格數的變化情況，具體過程參照文獻[18]。當計算得到的效率與水頭的外推相對誤差小于4%，最終網格方案包括600×104網格數，各計算區域的網格數為：蝸殼域22×104、固定導葉域79×104、活動導葉域121×104、轉輪域204×104、尾水管域80×104、上冠間隙和減壓孔及上冠空腔域共94×104。在葉片和上冠間隙流道處，控制近壁面y+的分布在300 以內，其中轉輪葉片的y+分布在30 以內，如圖4所示。

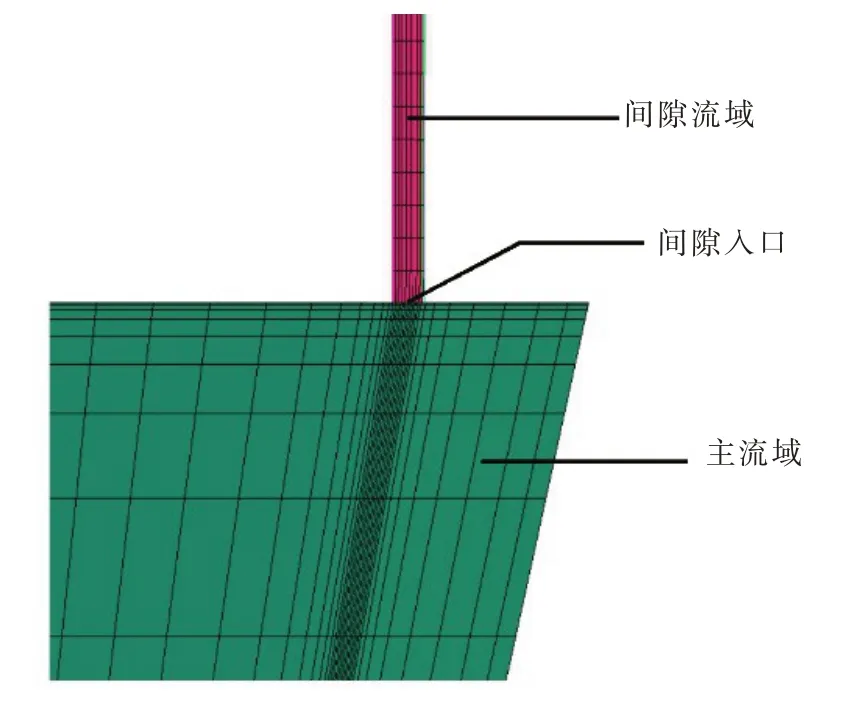
圖3 主流域與間隙流域過渡區域網格

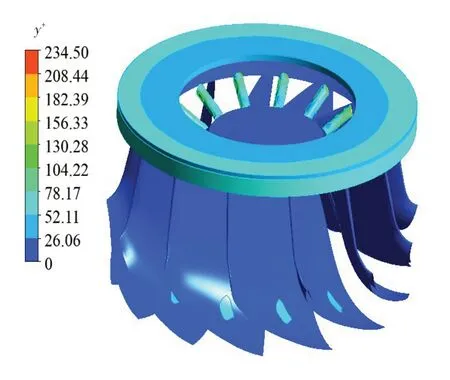
圖4 葉片和上冠間隙流道處壁面上y+分布

2.2 湍流模型和邊界條件本文采用Ansys CFX 軟件進行定常計算，采用不可壓縮流體連續方程和Reynolds 平均Navier-Stokes 方程模擬水輪機中的水體流動，采用SST k-ω湍流模型對方程組進行封閉[19-21]，它在預測近壁面流動或存在逆壓梯度流動等方面具有較大優勢。

蝸殼進口給定質量流量，水流方向垂直于進口斷面。出口條件采用平均靜壓為零。壁面條件采用無滑移邊界條件，臨近壁面區域采用標準壁面函數。其中轉輪和減壓孔區域定義在旋轉坐標下繞轉軸以水輪機轉速旋轉，動靜交界面采用凍結轉子。為了更好的模擬真實的流態，將上冠的壁面和泄水錐內壁面設為旋轉壁面2，求解方法采用精確性較好的高階求解，收斂精度為10-4。

3 內部流場計算結果與分析

3.1 性能對比為驗證數值計算的可靠性，對本文所研究的水電站水輪機進行真機試驗，并與考慮和不考慮上冠空腔及間隙的定常計算結果進行對比。試驗與計算均選取單位轉速n11=69 r/min，單位流量為0.6Qd、0.8Qd、Qd、1.08Qd和1.2Qd共5個流量工況點，5個工況具體流量分別為0.459 m3/s、0.612 m3/s、0.765 m3/s、0.826 m3/s和0.918 m3/s，5個 工 況 點對 應的活動導葉開度分別為9.7、13、16、18和21 mm。由圖5可以看出定常計算結果與試驗結果相差不大，在1.08Qd時出現最大誤差為1.89%，NUCCS 計算所得的各點效率明顯高于UCCS，因為NUCCS的計算沒有考慮容積損失，UCCS的計算考慮了間隙流動和容積損失，所以考慮上冠空腔和上冠間隙的數值計算結果更接近試驗結果，其最大誤差為1.4%。

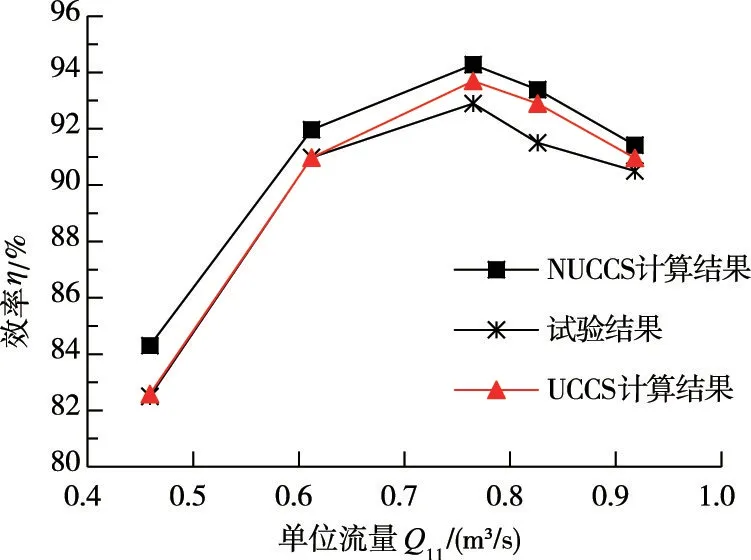
圖5 數值模擬結果與試驗結果對比

3.2 轉輪流態分布為了探究考慮上冠間隙及空腔對水輪機內流態的影響，將設計工況下UCCS和NUCCS的轉輪壓力場及渦流黏度分布進行比較，圖6為NUCCS和UCCS的轉輪內靜壓力分布，從圖6可以看出，轉輪葉片正面為正壓，而葉片背面有一定的負壓，這樣的壓差促使葉片旋轉。對比圖6的轉輪靜壓力分布圖，可以看出UCCS的水輪機結構在泄水錐處的負壓比沒有考慮空腔的小，NUCCS的水輪機在泄水錐及尾水管的中心部分形成較大的負壓區，從而產生不穩定流態，當流道內形成了壓力值低于對應溫度下水流飽和蒸氣壓的低壓區時，就會產生渦帶，如果使流道中部分區域的壓力升高，就會減弱渦帶，UCCS的轉輪空腔內的壓力和泄水錐附近的負壓相抵消，在泄水錐處并沒有產生很大的負壓區，所以減少了泄水錐處的渦帶產生。

圖7為NUCCS和UCCS的轉輪內渦流黏度分布，從圖7可以看出，NUCCS 在泄水錐處流態較混亂，可能產生渦量，UCCS 雖然在泄水錐處流態更穩定，但在上冠空腔內的流態較為混亂，因其結構尺寸變化較大，可能產生更大的渦量，考慮到間隙泄漏流量為0.000 17 m3/s，為總流量的0.332%，泄漏流量占主流的百分比較少，間隙泄漏流量對水輪機結構特性的影響，將在第3 節分析。

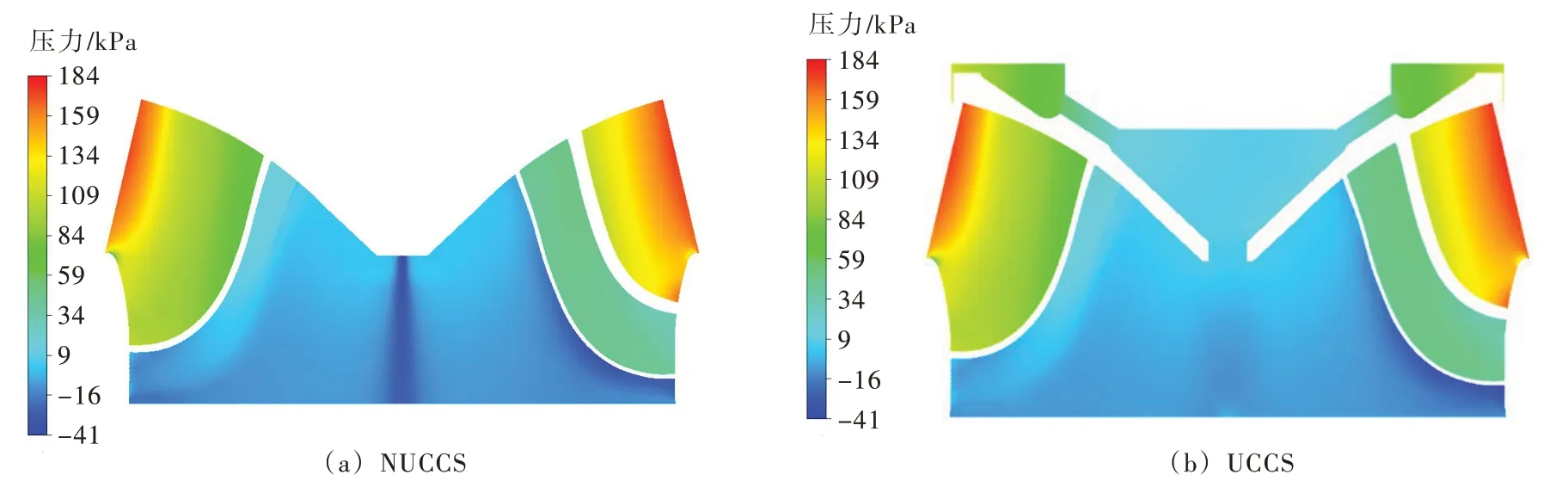
圖6 轉輪內靜壓力分布

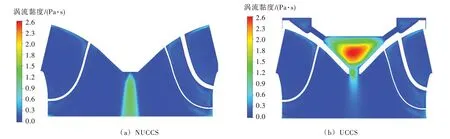
圖7 轉輪內渦流黏度分布

3.3 上冠間隙及空腔處的流態圖8是上冠間隙入口及上冠與蓋板之間空腔的速度等值線分布。從圖8可以看出，水流剛進入間隙，因為流道斷面面積突然縮小，所以流速較大，進入腔體后隨著流道面積擴大，流速又逐漸減小。由于水輪機上冠壁面具有一定的旋轉速度，故空腔內靠近下壁面的水流速度都較大，上壁面是靜止的水輪機蓋板的一部分，其附近流速較小。

圖9為上冠間隙流道內水流的跡線，因為流道斷面面積逐漸增大，間隙流道內壓力由間隙入口到泄水錐處呈逐漸減小趨勢，由跡線圖可以看出高速水流由間隙入口進入，沿上冠壁面呈螺旋狀軌跡進入減壓孔，由于減壓孔入口處水流具有較大環量，所以水流在減壓孔進口處與管壁不斷撞擊形成了部分高壓區，最后進入泄水錐內水流流態紊亂。水流從間隙入口進入，通過減壓孔，再由泄水錐排出，此過程中水流流速逐漸減小。

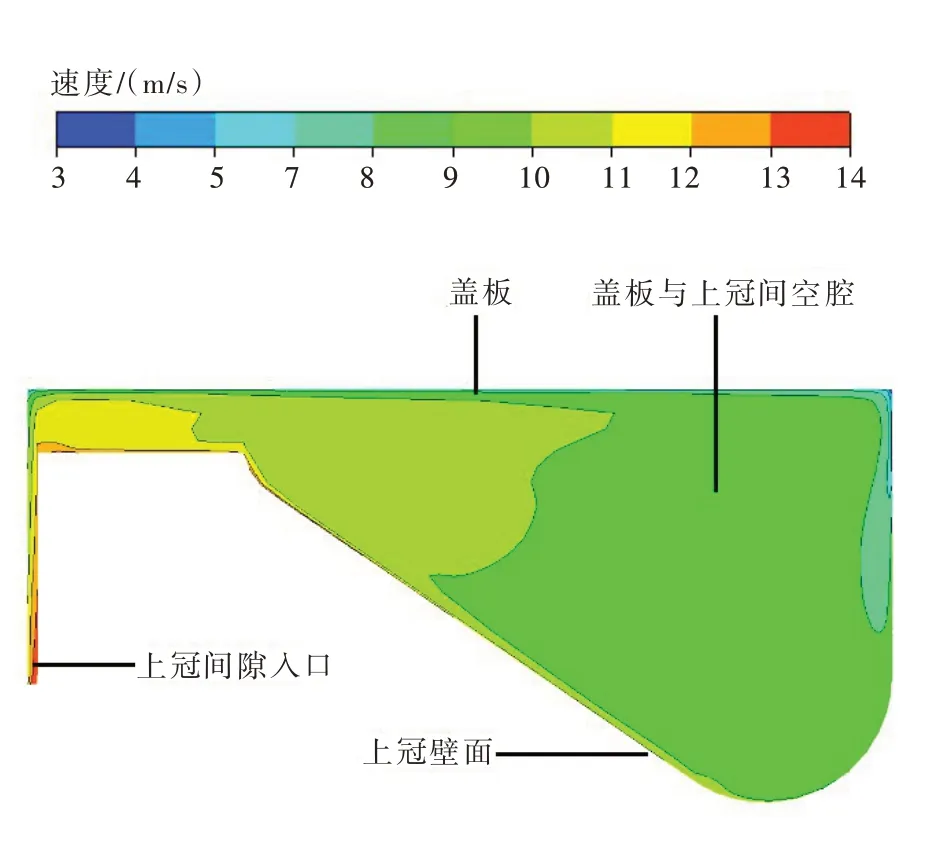
圖8 上冠間隙軸面圖的速度等值線分布

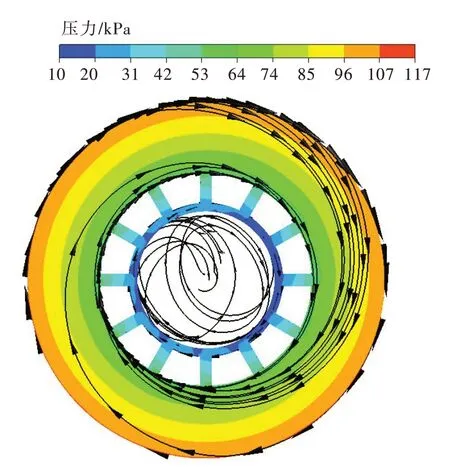
圖9 上冠間隙流道壓力分布與跡線

圖10是泄水錐出口的流態圖，上冠在旋轉的同時，由泄水錐向外排出間隙泄漏的水，水流因為具有較大的圓周速度而與空腔的壁面產生碰撞，所以在出口壁面處產生壓力較大的區域，水流速度矢量的方向因壁面旋轉而產生變化，由圖10可以看出間隙流量在泄水錐出口處流態較為穩定，泄水錐出口處的低壓區域并不位于圓形出口的幾何中心，這是因為空腔內水流因為外壁面的旋轉，其壓力分布整體呈現周期性變化，空腔內低壓區域及高壓區域隨著上冠的旋轉而改變位置，由此可以看出空腔內的流態特性。數值計算得出3個流量工況0.8Qd、Qd和1.2Qd的流場結果，對3個工況下的空腔內的渦量分布進行對比，圖11為不同工況下上冠空腔內渦量分析，其中在大流量工況1.2Qd下間隙流量較大，其渦量分布也較大，因為結構尺寸突變會產生較大的渦量，所以三者的主要渦量分布區域都在減壓孔入口處和泄水錐出口處。

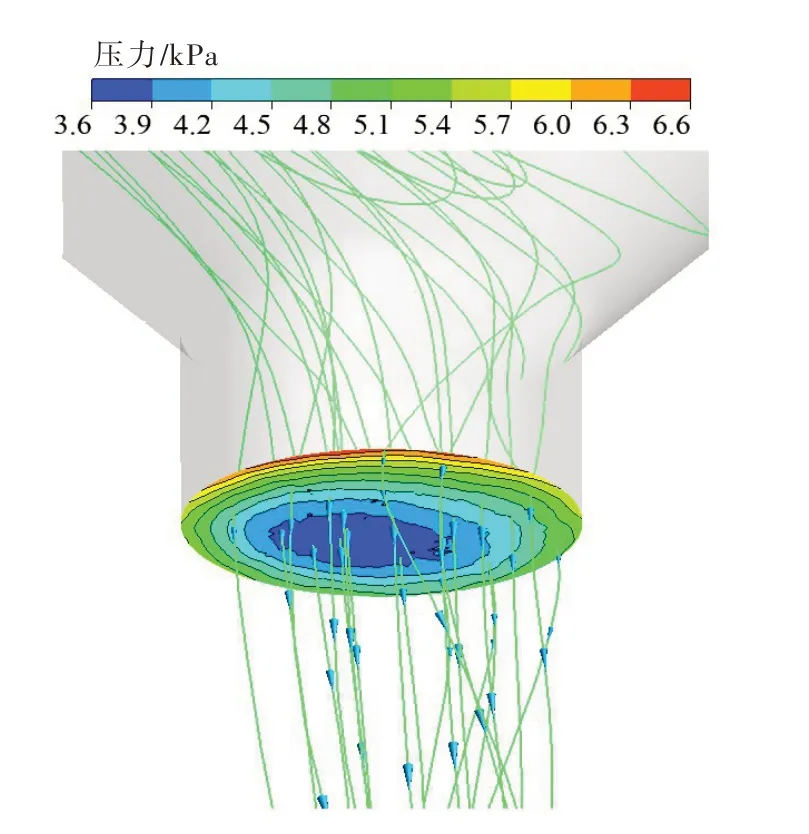
圖10 泄水錐出口流態

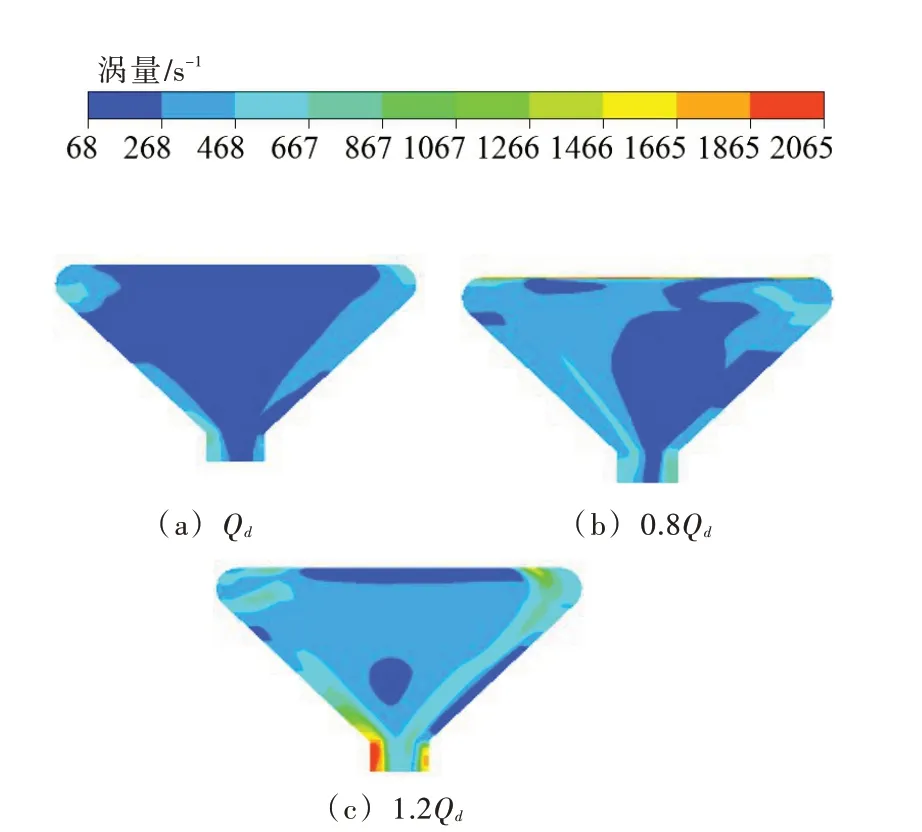
圖11 3種工況下空腔內渦量分布

3.4 上冠空腔對尾水管內流態的影響圖12對比了在設計流量下，NUCCS和UCCS的尾水管流線分布，可以看出考慮上冠空腔間隙流后，尾水管內的流態更加惡化，其支墩兩側的脫流現象更加嚴重，原因是因為轉輪上冠空腔內的間隙流動使得轉輪出口處流速分布更不均勻。

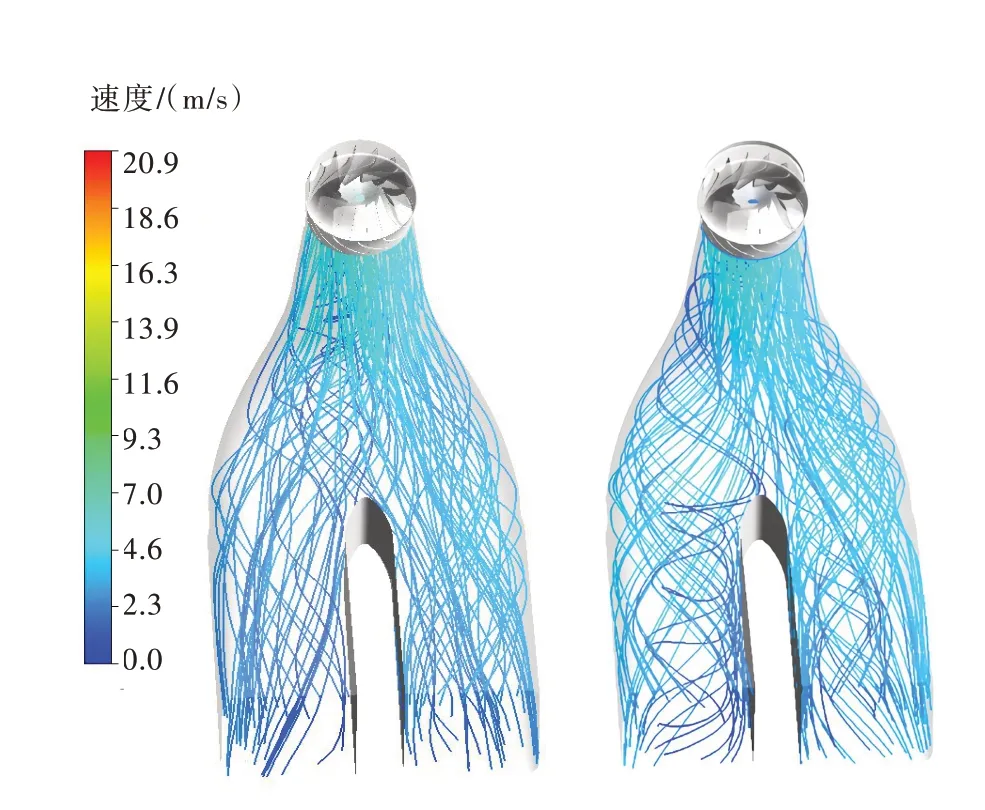
圖12 NUCCS(左)與UCCS(右)尾水管內流線

4 流固耦合計算結果

4.1 流固耦合分析以上述定常計算結果為初始值進行非定常計算，在計算中時間步長設置為轉動周期的1/120，為0.000 476 1 s，一個周期為0.0571 s。采用UG進行轉輪結構的實體建模，并導入AN?SYS進行有限元網格劃分，以轉輪應力分布為評判標準進行轉輪域的網格無關性驗證，最終確定網格數為163×104，轉輪有限元模型如圖13所示。

圖13 轉輪有限元模型

該轉輪材料為06Cr13Ni4Mo（密度為7850 kg/m3；彈性模量為210 GPa，泊松比為0.3），對轉輪采用單向瞬態流固耦合方法，流固耦合固體的邊界條件包括約束條件與載荷條件兩種，約束條件是在水輪機與主軸相連的橫截面上設置全約束，載荷有重力載荷和離心力載荷，以及加載非定常計算穩定后的最后一個周期的流場壓力，在考慮間隙流的計算中，要在上冠空腔和間隙流道壁面上加載相應的流場壓力，不考慮間隙流的計算則只加載葉片表面、上冠和下環內表面的流場壓力。為了使考慮和不考慮間隙及空腔的兩種流固耦合的計算結果具有可比性，不僅兩種算法邊界條件設置、網格劃分完全一致，流體域、結構域對應的求解器設置也完全一致[22]。

計算得到了轉輪應力、變形隨時間變化的情況。作為代表，表2 給出了一個周期內不同時刻轉輪的最大應力值和最大位移。可以發現，在各時刻下最大位移變形都發生在靠近葉片與上冠連接處的出水邊，在時刻t=0.1857 s 出現最大應力值和最大變形位移量，轉輪應力最大應力位置出現在葉片與上冠連接處。

因為在設計流量Qd下水輪機處于最優工況，不能充分說明上冠空腔結構對轉輪葉片的影響，所以分別對轉輪處于小流量工況0.8Qd、設計工況Qd和大流量工況1.2Qd下進行流固耦合計算，圖14為一個周期內某一時刻t=0.1857 s時轉輪的應力分布，圖15為轉輪在該時刻的總變形圖。表3為該時刻下3種工況下轉輪最大等效應力值和最大變形量的對比，其中影響系數為NUCCS和UCCS 數值的差與不考慮空腔數值的比值。

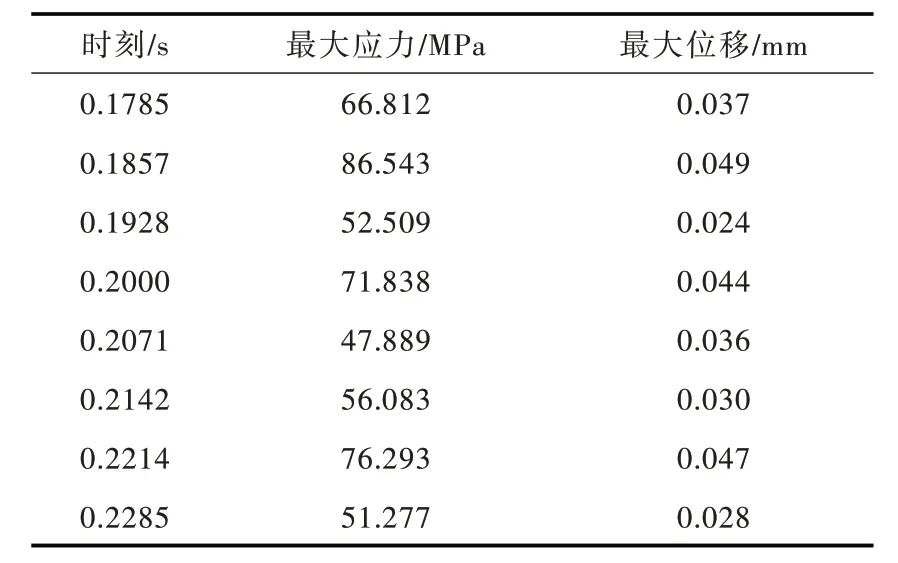
表2 各時刻下轉輪最大等效應力與最大變形量

由圖14可以看出，水輪機在3種不同流量工況下，等效應力主要分布在葉片與上冠連接處的附近區域，以及葉片靠近上冠的出水邊，這是因為在水輪機與主軸相連的橫截面上設置了固定約束，在加載了轉輪表面流場壓力后，葉片靠近固定約束處的彎矩和剪力較大，無法通過彎曲或變形釋放應力，表明計算結果符合結構力學特性，且與文獻[23-24]數值計算結果基本一致。葉片背面有較大面積的應力集中現象。最大等效應力點幾乎都出現在葉片與上冠的連接處，這與其他研究結果基本符合[25]，在流量工況1.2Qd下考慮上冠空腔及間隙時，轉輪最大等效應力出現在葉片與上冠的連接處的進水邊。由表3看出，3種工況下考慮上冠空腔及間隙后，轉輪的最大等效應力及最大變形量均減小，其原因是上冠間隙對于主流道流量產生了分流，主流道流量減少，轉輪葉片所受水壓力就減小，轉輪的等效應力和變形量就會減小，與此同時，上冠空腔及間隙內也有水壓力的作用，抵消了一部分主流道內不利于轉輪結構的流場壓力，所以轉輪最大變形量減小，由2.2 節流場結果分析得知，空腔改善了轉輪出口的流態，減小了渦量的產生，這也改善了轉輪結構的力學特性。

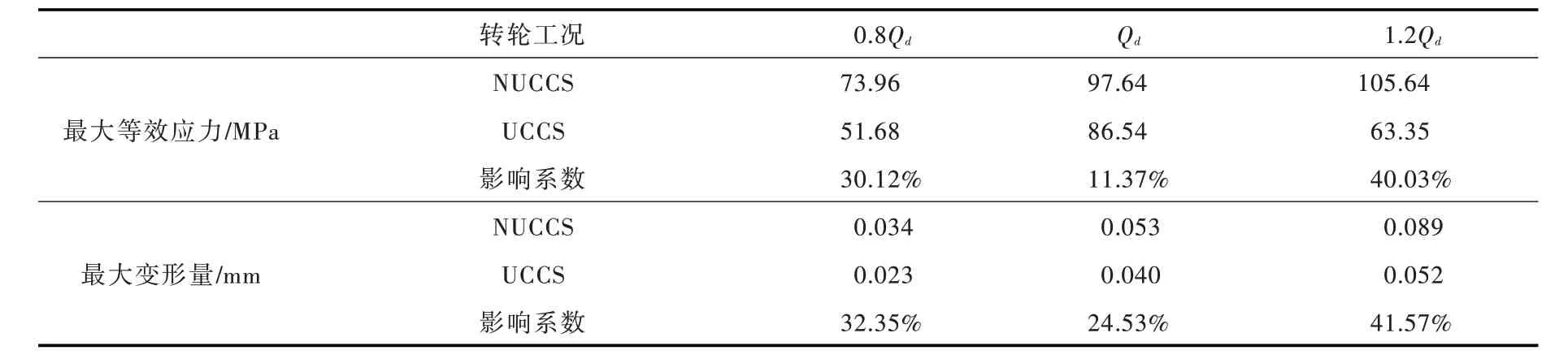
表3 t=0.1857s時轉輪最大等效應力與最大變形量對比

由圖15看出，隨著流量的增加，轉輪最大變形量逐漸增大，流量工況0.8Qd下轉輪的最大變形量出現在葉片靠近下環的部分，其余工況下最大變形出現在葉片靠近上冠的部位，且都出現在出水邊，因為葉片出水邊厚度較薄，剛度和強度不足，所以造成了應力集中及最大變形量出現在葉片的出水邊。隨著流量的增大，轉輪變形量的變化與等效應力的變化一致，都呈現出增大的趨勢。由表3中的影響系數看出，NUCCS和UCCS的計算結果相差較大，其中在最優工況Qd下的影響系數比其他兩個工況下的小，間隙及上冠空腔對瞬態轉輪結構分析的影響是較大的，故在瞬態流固耦合計算中，間隙流域的分析是尤為必要的。

4.2 模態分析上冠空腔及間隙受到水壓力作用，考慮其對機組穩定性及轉輪的振動特性產生的影響，所以對NUCCS和UCCS的轉輪分別進行預應力模態分析。計算發現考慮與不考慮上冠空腔兩者振型基本一致，因此，文中只列出了具有代表性的UCCS的轉輪前6階振型，圖16為UCCS的振型，表4為前6階振動頻率對比，變化率為不考慮空腔和考慮空腔數值的差與不考慮空腔數值的比值。

變化率越大表明NUCCS和UCCS的模態分析計算結果差距越大，由表4所示兩者固定頻率的變化率在2階模態時最大，為0.064%，兩者計算得出的振型基本一致，因此考慮上冠空腔及間隙對水輪機固有頻率和水輪機振型影響較小。

由圖16可以看出轉輪葉片及下環部分形變量較大，1階振型主要表現為沿軸向方向上下振動，下環變形量較大，2、3和6階振型主要表現為下環和葉片的彎曲變形，4、5階振型則表現為主要表現為類似于鐘擺的整體擺動，1階振型的最大變形出現在下環，其余階次的最大變形皆出現在葉片出水邊靠近上冠的部分。

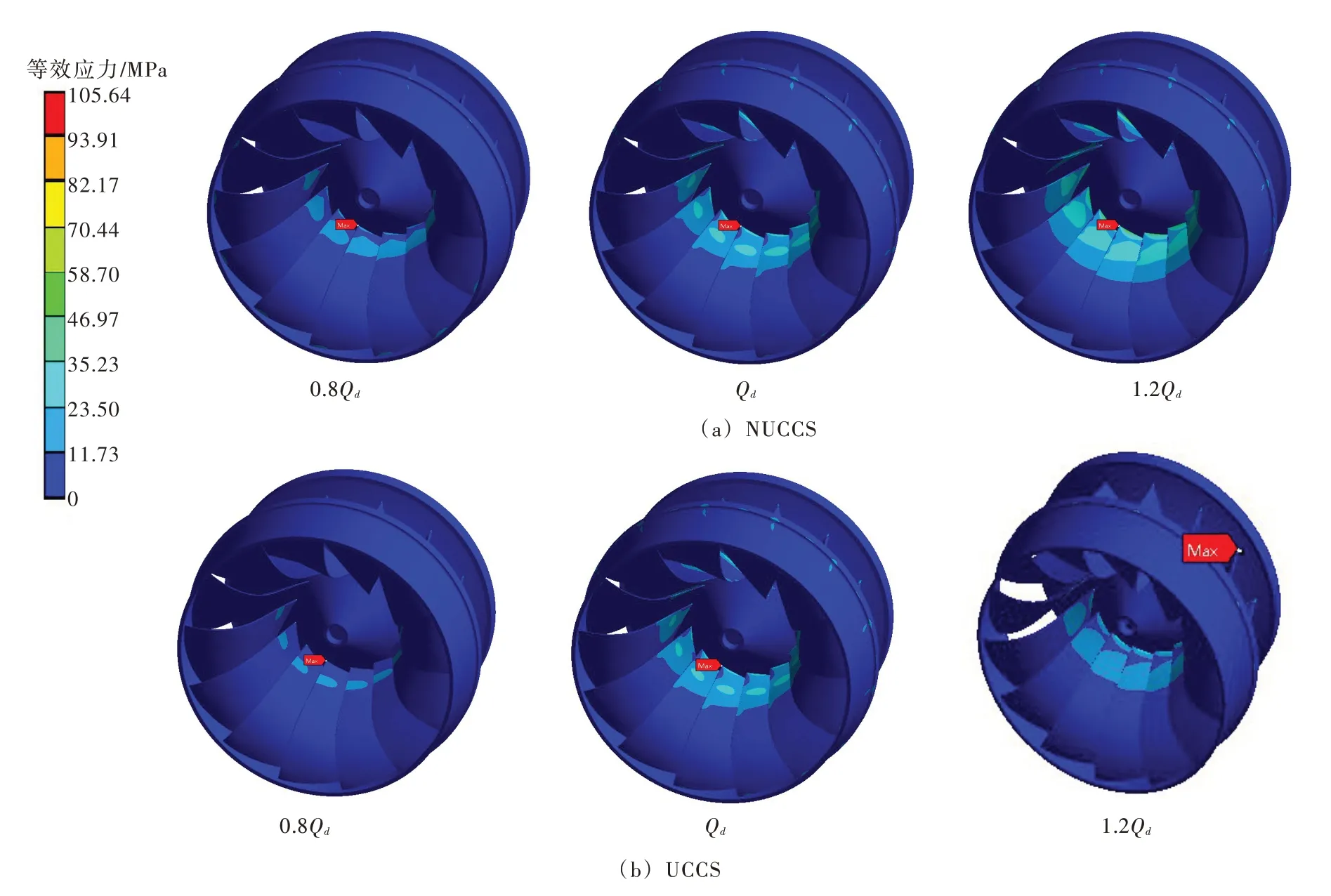
圖14 3種工況下等效應力分布

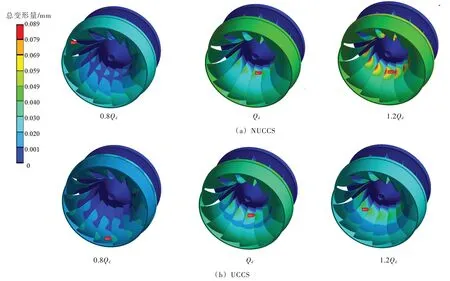
圖15 3種工況下總變形量

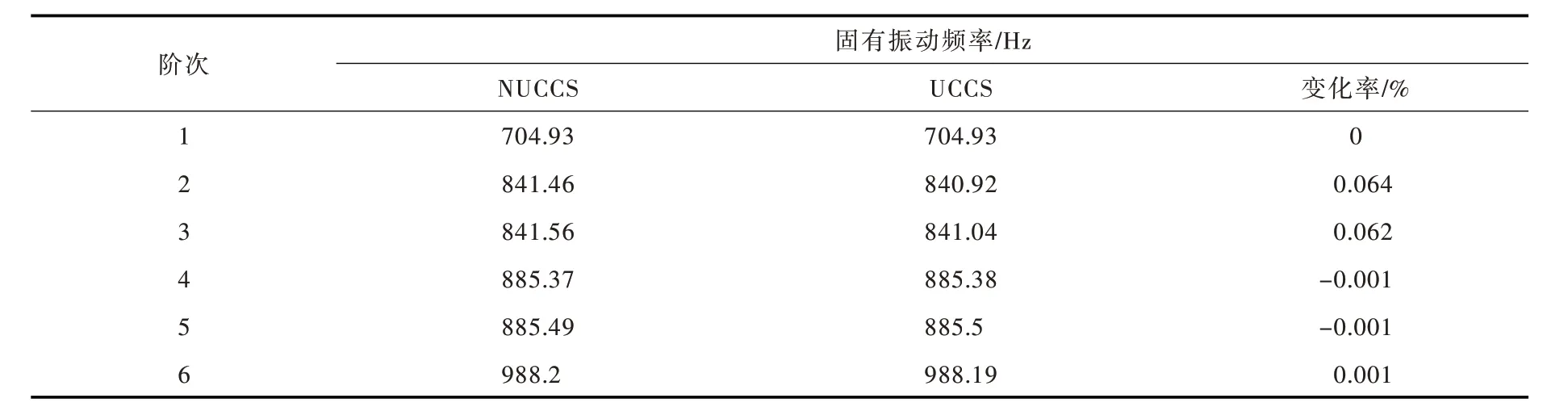
表4 水輪機轉輪前6階模態固有振動頻率

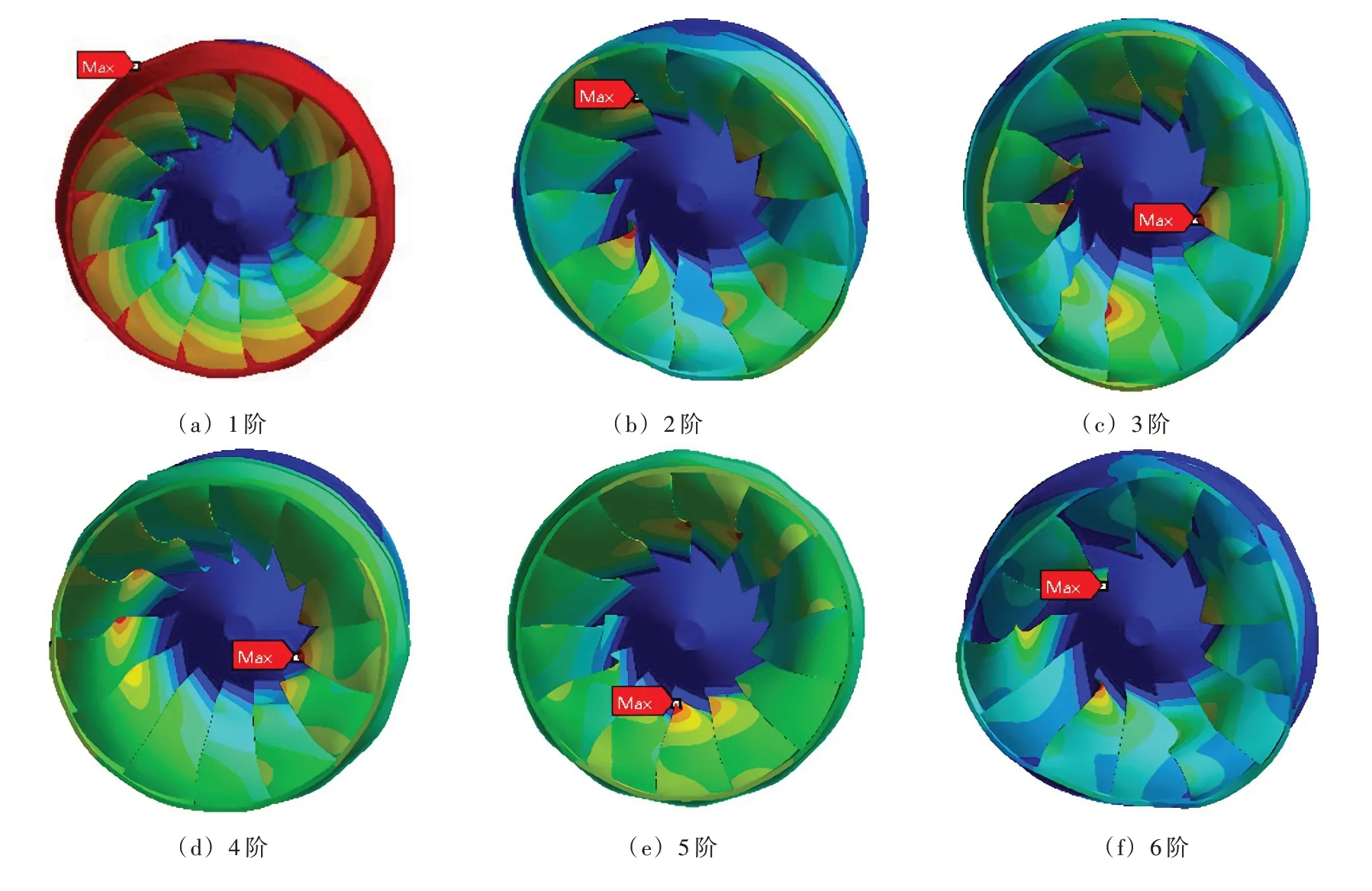
圖16 UCCS的預應力模態前6階振型

5 結論

（1）混流式水輪機中的上冠空腔結構會一定程度減小泄水錐的負壓力，減小轉輪出口的渦量分布。相比NUCCS的轉輪的流固耦合計算結果，UCCS的轉輪的最大等效應力和最大變形量都較小。轉輪在大流量工況下葉片受力大，其應力集中區域和大變形量主要分布在葉片靠近上冠的部分，在小流量工況下葉片受力較小，但其等效應力及變形量主要分布于葉片靠近下環的位置。

（2）在3種流量工況0.8Qd、Qd和1.2Qd下，進行了轉輪的瞬態流固耦合分析，上冠空腔及間隙對轉輪的瞬態結構力學分析結果的影響較大，最大的影響系數為41.57%，其中NUCCS和UCCS 兩者最大等效應力的差值最大為42.29 MPa，最大變形量的差值最大為0.037 mm。

（3）UCCS的轉輪和NUCCS的轉輪兩者的固有頻率的最大變化率為0.064%，且UCCS的轉輪各階次振型與NUCCS的轉輪振型基本一致。