不同布設方式的生態浮床對水流結構影響研究

高翼天，祝 求，黃宇云，余明輝，周志華

（1.武漢大學 水資源與水電工程科學國家重點實驗室，湖北 武漢 430072；2.清華大學 水利水電工程系，北京 100083；3.天津市水利科學研究院，天津 300061）

1 研究背景

目前我國眾多江河湖泊存在不同程度的污染。為應對水質惡化、水生態破壞的問題，生態浮床被廣泛地應用在污染水域凈化水質。生態浮床是利用無土栽培技術，以高分子材料作為基質和載體，利用植物根系吸收、微生物降解、分泌物反應等過程實現水體修復的技術[1]；另一方面，生態浮床會干擾水流結構，降低河道行洪排澇能力，形成安全隱患。因此，研究生態浮床對水流結構影響，從減小對洪水位壅高及利于污染物擴散的角度優化生態浮床的布設方式是必 要的[2]。

目前，研究生態浮床對水流結構的影響主要采用物理模型或數學模型。物理模型法利用室內水槽試驗，采用多普勒測速儀等儀器監測水動力參數的變化規律。朱紅鈞[3]、黃本勝等[4]及何寧等[5]研究設置有生態種植圈或被水葫蘆等漂浮植物覆蓋的河道水動力特性，發現水位沿程均有壅高，水流縱向流速增加，垂線流速呈現水面和底壁流速小中間流速大的分布情況。槐文信等[6]研究明渠漂浮植被水流內部能量損失和傳遞規律，發現斷面上的能量損失主要集中在漂浮植被區，并且在植被區和非植被區的交界面達到最大。周志華等[7]研究了不同水流條件、不同布置形式下生態浮床對河道水流阻力特性的影響。結果表明，生態浮床增加了水流阻力，造成上游水位壅高，流經生態浮床附近的水流流速迅速降低，床體兩側渦紋明顯。數學模型法是利用CFD 技術構建三維數學模型，對生態浮床的數值概化主要分為兩類：（1）生態浮床概化為單層式固定多孔介質域，整個多孔介質具有同一孔隙率。如黃本勝等[4]、王潔瓊等[8]研究了被水葫蘆覆蓋的河道的水位壅高和流速分布情況，唐漪[9]研究了生態浮床的水動力特性。李勇等[10]研究了雙浮床串列、并列和錯開三種排列方式對水流水動力特性的影響。除生態浮床外，植物覆蓋區也普遍被概化為多孔介質進行數值模擬[11-12]。該方法的模型構建較簡單，但是未考慮生態浮床實際分層結構。（2）生態浮床概化為兩層式可浮動多孔介質域，包括不透水的浮床主體區和可透水的浮床根系區。如Rao 等[13-14]利用該概化方法研究在不同浮床間距、不同流速、不同根系孔隙率的條件下生態浮床的污染物去除效果和水動力特性，發現當浮床覆蓋率越大或者并列浮床間距越小時，上游壅高效果越明顯。該方法需要使用動網格技術，網格精度要求高，計算時間較長。

本文運用兩層式固定多孔介質域概化模擬生態浮床，分為低透水性的浮床主體區和高透水性的浮床根系區，構建生態浮床不同布設方式的水槽三維水動力數學模型，研究生態浮床的水動力特性，對比分析無浮床、浮床串聯排列、浮床不同間距交錯排列等多種工況的水槽水流結構特征及其變化規律，為河道治理規劃、設計和施工及管理提供科學依據。

2 方法

基于FLUENT 軟件建立設有生態浮床的水槽三維水動力數學模型，研究不同布設方式的生態浮床對水動力特性的影響。

2.1 基本方程使用三維瞬態流運動模式，基本控制方程包括連續性方程和動量守恒方程。

使用標準k-ε紊流模型，近壁處理采用標準壁面函數，基本方程包括：

k 方程：

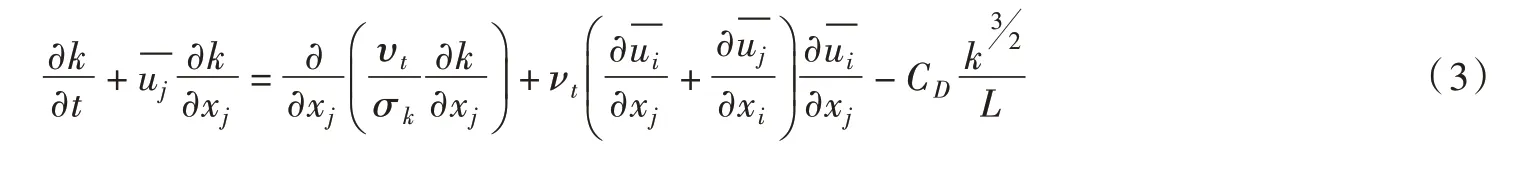
ε方程：

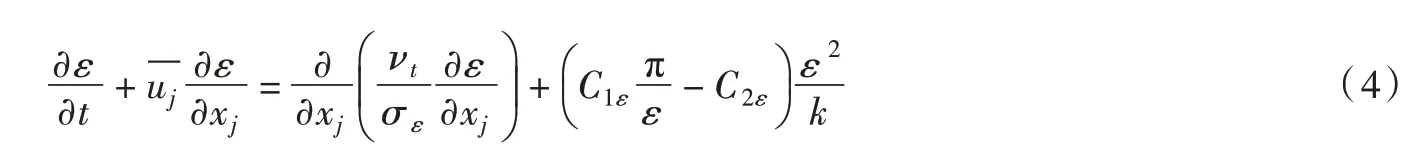
式中：xi為笛卡爾坐標系坐標，x1、x2、x3分別代表x、y、z方向；fi為沿x、y、z 三個方向中某一方向的加速度；ui為沿x、y、z 三個方向中某一方向的瞬時速度分量；為沿x、y、z 三個方向中某一方向的時均速度分量；k為紊流動能；ε為紊流耗散率；p為當地大氣壓強；ρ為流體密度；ν為運動黏度；νt為渦黏度；C1ε、C2ε、CD、σk、σε為經驗系數，分別可取值為1.44、1.92、0.09、1.0、1.3。

2.2 生態浮床的多孔介質域概化生態浮床包括用于托放植物的浮床主體及上托植物兩部分。如圖1所示，部分浮床主體區、浮床根系區淹沒在水面下。浮床主體一般由聚乙烯等材料制成，以繩索系于床底，浮床主體區孔隙率比植物根系區小。

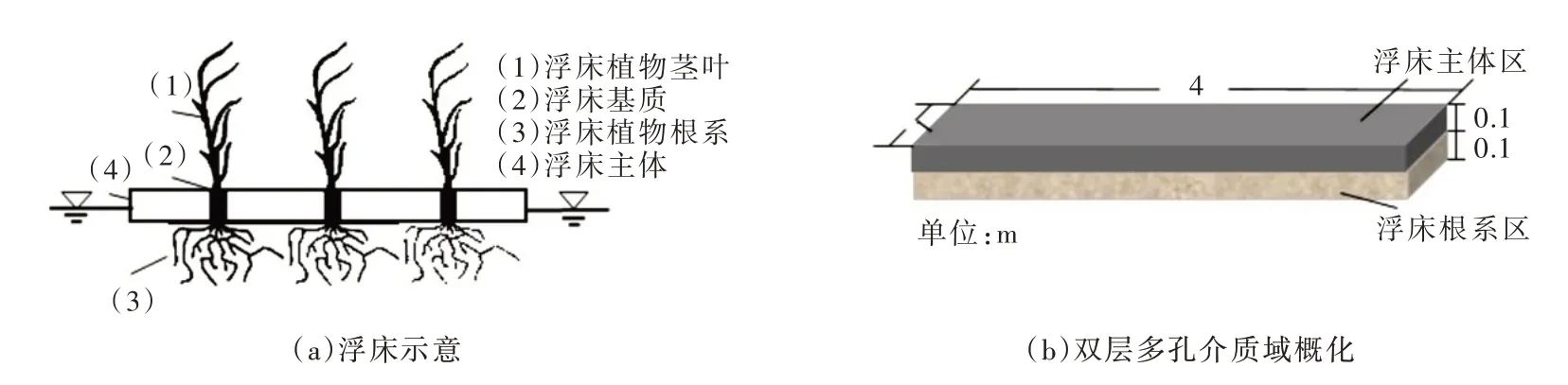
圖1 生態浮床概化示意圖

本文將生態浮床概化為固定多孔介質域。考慮到浮床主體區域與根系區域孔隙率及對水流阻礙作用不同，將多孔介質域區分為兩層，上層為低透水性的浮床主體區，下層為高透水性的浮床根系區，采用不同透水率與阻力系數反映主體區與根系區的阻水效果。多孔介質模型采用經驗公式計算多孔介質對于流動產生的阻力，即在三維數學模型動量守恒方程上考慮動量消耗的源項，即：

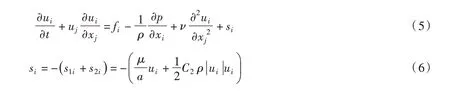
式中：si為沿x、y、z 三個方向中某一方向的動量源項，包括黏性阻力損失項s1i和慣性阻力損失項s2i；為黏性阻力系數；C2為慣性阻力系數。

黏性阻力系數與慣性阻力系數運用Ergun 公式關聯：

式中：Dp為多孔介質的當量直徑，根據實測水面線試算；ε為孔隙率。

2.3 求解方法FLUENT 利用有限體積法建立離散方程進行數值計算求解原控制方程。離散方程的數值求解采用SIMPLE 算法，壓力離散格式采用Body Force Weighted 模式，動量、體積分數、紊流擴散系數等離散均使用一階迎風模式。采用VOF（Volume of Fluid）方法追蹤自由面，VOF方法能比較方便地處理自由面大變形和自由面拓撲結構發生變化等復雜情況[4]。所遵循的體積分數連續方程如下：

式中：F1為多相流某一種流體的體積分數；ui為沿x、y、z 三個方向中某一方向的速度分量。

2.4 布設生態浮床的水槽三維水動力模型以文獻[7]水槽試驗為背景建立生態浮床的水槽三維水動力模型，如圖2所示。

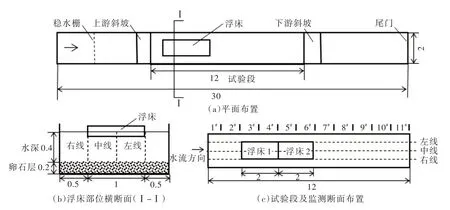
圖2 水槽試驗布置（單位：m）

試驗水槽全長30 m，試驗段長12 m，寬2 m、高0.9 m，水槽床面坡度i=0。水槽兩側壁面為玻璃面，底部鋪設碎石子厚20 cm。生態浮床是由多個小型浮床組成的2 m（長）×1 m（寬）×0.2 m（厚）長方形，植物黃菖蒲根系長10～15 cm。試驗工況包括無浮床及兩浮床居中無間距串聯排列。在試驗段x=0.75～11.25 m之間設置9個間隔為1.05 m的測量橫斷面，分別記作斷面1#—11#，每個斷面取左、中、右線，垂線方向取6個流速測點。流速測量采用聲學多普勒流速測量儀（ADV），頻率200 Hz。水位測量采用水位測針，精度為0.1 mm。水槽進口流量0.32 m3/s，出口水位0.4 m。

2.4.1 模擬范圍及網格劃分 模擬范圍為水槽試驗段，如圖2（c）。模型采用結構化六面體網格。經優化比選，網格長、寬、高尺寸分別取為0.05、0.1、0.02 m。在底壁附近及水面線附近局部加密。

2.4.2 邊界條件及計算步長 水槽進口流量0.32 m3/s，出口水位0.4 m。水流進口邊界采用速度進口邊界條件ux=0.4 m/s，空氣進口邊界采用壓力進口邊界條件，進口壓強設為大氣壓；出口邊界條件包括水流、空氣混合出口邊界條件，采用壓力出口邊界條件，出口壓強設為大氣壓，并控制出口水位；固壁條件采用無滑移邊界。時間步長0.05 s，每個時間步長內的最大迭代次數為20 次。

2.4.3 計算參數設置及率定 （1）糙率相關系數。運用水槽試驗成果[7]率定，粗糙度取0.035 m，粗糙度常數為0.8。（2）紊流相關系數。因明渠流紊流結構的特殊性，紊流強度計算較為復雜。計算中紊流強度試算值借用充分發展的管流I=0.16Re-0.125=0.0373=3.7%[15-16]。雖然試算值存在誤差，但不改變收斂解成果的規律性。（3）多孔介質參數。①孔隙率，根據生態浮床組成特征，取主體區孔隙率約為0.1，根系部分孔隙率約為0.65[5，13]。②阻力系數，假定多孔介質為各向異性、均勻的剛性介質。在模型中，首先假定生態浮床的浮床根系區起主要阻水作用，將生態浮床視為單層式多孔介質域，試算阻力系數并擬合水面線，擬合效果最好的阻力系數可以等同于根系區的阻力系數。然后，利用兩層式多孔介質域試算浮床主體區阻力系數。經試算得沿x方向黏性阻力系數、慣性阻力系數，浮床根系區分別為7.2×107、4600，主體區分別設置為2.5×108、143 000。考慮到浮床阻力系數的各向異性，根據實測值擬合將沿y、z方向的黏性阻力系數設置為沿x方向黏性阻力系數的0.1～100倍[17]。

2.4.4 模型驗證 運用兩浮床居中無間距串聯排列工況水槽試驗成果驗證模型。進出口邊界條件同水槽試驗。水面高程云圖及水槽中線水面線、各測速斷面中線流速垂線分布數模計算與水槽試驗成果對比見圖3。從圖3可以看出，二者吻合良好，水面線擬合的納什效率系數為0.95。說明模型參數選取合理，模擬精度較高。

浮床段流速垂線分布呈水面和底壁附近流速較小中間流速較大的“紡錘型”。從水力學角度，由于浮床段表面流速一般很小，幾乎可以忽略不計，所以可將其等效為植被河床邊壁。按阻力劃分過流斷面的方法，沿水深方向分成兩層等效明渠流流動層（浮床下層和床面上層）。假設兩層之間沒有相互作用，兩層分別受植被底部和床面粗糙程度影響，則每層流速分布為對數分布，在沿垂線方向的中間位置存在最大流速[18]。

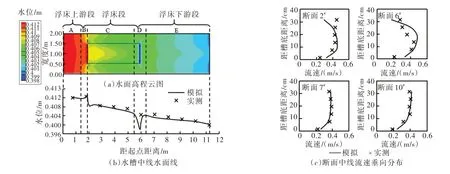
圖3 數模計算與水槽試驗結果對比

3 結果及討論

3.1 計算工況為了研究無浮床、浮床不同間距串聯或交錯排列（如圖4所示）等不同布設方式的生態浮床對水流結構的影響，設置14 組計算工況如表1所示，文中浮床相對間距為浮床間距/浮床長度（2 m）的相對值。水槽進口流量0.32 m3/s，出口水位0.4 m。

表1 計算工況

3.2 計算結果

3.2.1 水面線

（1）浮床無間距排列相較于無浮床工況。如圖3（a）所示，沿程劃分為A—E 共5個區。布設生態浮床后，無論是串聯排列方式還是交錯排列方式，A、B 兩個區均出現明顯的壅水現象，C 區由于浮床阻水作用導致水流損失部分動能，浮床內部水面線下降緩慢均勻。由于不同流速水流相互摻混，進入D 區后水面線出現一定的波動。E 段進入浮床下游段，水面線平緩恢復。分別取斷面1#—2#和斷面7#—11#的水面壅高平均值為浮床上、下游水面平均壅高值。如圖5所示，與無浮床工況相比交錯排列水位相對壅高度沿程均高于串聯排列，并且在浮床上游段，串聯排列、交錯排列水面平均壅高值分別為0.65 cm、1.20 cm，為出口水深的1.625%、3%，文中稱水位相對壅高度。

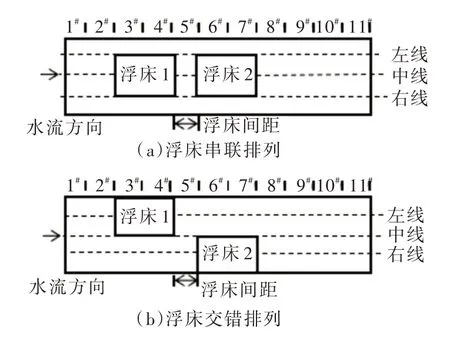
圖4 浮床串聯及交錯排列示意圖

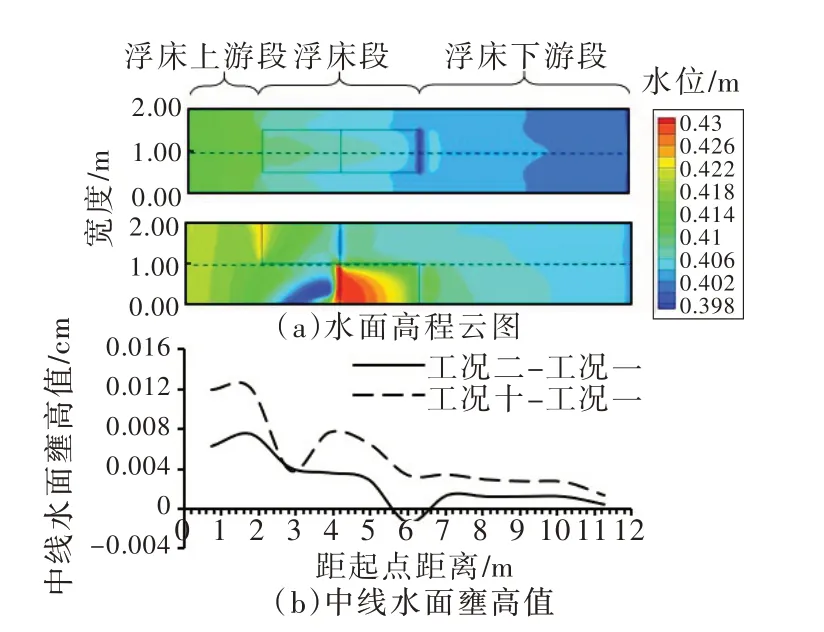
圖5 水面線變化

浮床居中串聯排列情況下，浮床上下游中線水位均略大于左右線；浮床交錯排列情況下，水槽水位出現明顯的不對稱性，浮床上游水位左線＞中線＞右線，浮床下游水位右線＞中線＞左線。

（2）浮床不同間距串聯排列對比。如圖6所示，隨著浮床相對間距的不斷增大，與無浮床工況相比，浮床串聯排列工況的上游段水位相對壅高，當相對間距大于50%時，增長幅度變緩，水位相對壅高度趨于穩定；浮床下游水位相對壅高度隨間距的增加呈現先減小后增大的趨勢，在相對間距為5%時水位相對壅高度最小，且當相對間距大于50%時，水面壅高增加幅度變緩。

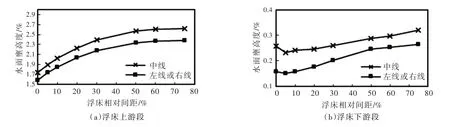
圖6 浮床不同相對間距串聯排列工況水位相對壅高度

（3）浮床不同間距交錯排列對比。如圖7所示，隨著浮床間距的增大，浮床上游水位相對壅高度不斷減小，當相對間距大于10%時，左、中、右線水位相對壅高度趨于穩定；浮床下游水位相對壅高度也不斷減小，且當相對間距大于20%時，水位相對壅高度趨于穩定。

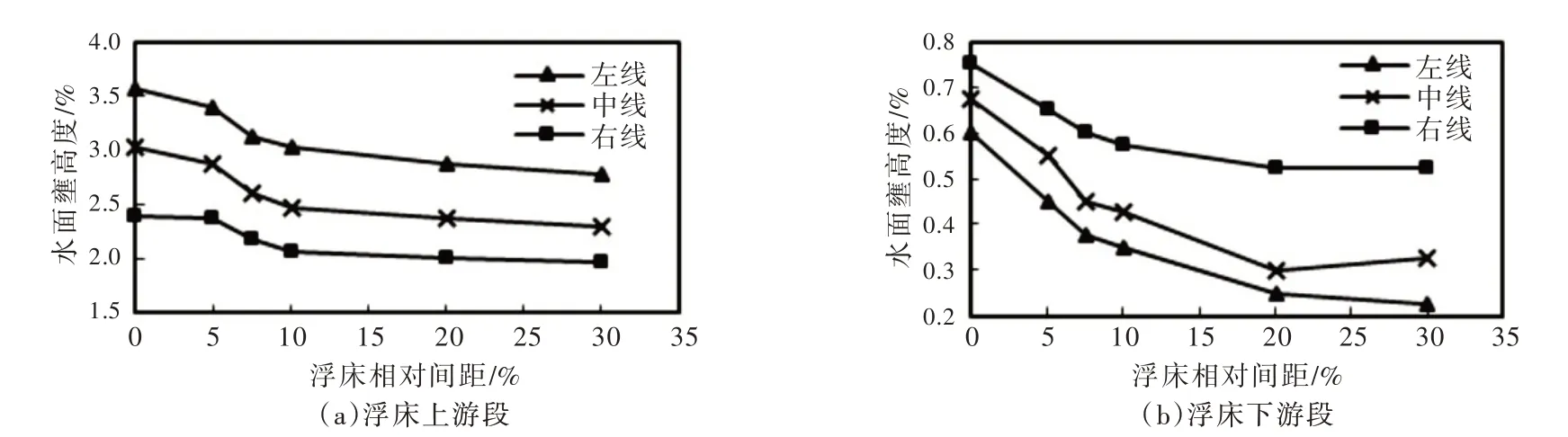
圖7 浮床不同相對間距交錯排列工況水位相對壅高度

3.2.2 流速 考慮到沿y、z方向的流速相對較小，重點研究沿x方向的流速分布變化規律。

（1）浮床段流速垂線分布特征。以工況二為例，如圖8所示，沿水槽中線，位于浮床段的C區垂線平均流速明顯增大。浮床迎流頭部附近垂向流速呈現水面和底壁附近流速較小、中間部分流速較大的“紡錘形”。在浮床段、浮床下游段，最大流速區分布在浮床兩側及下方水體中。

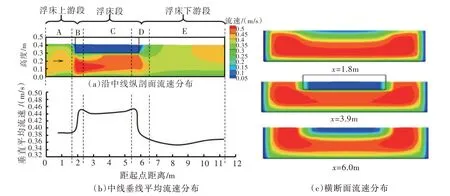
圖8 串聯浮床工況流速分布

（2）浮床不同間距串聯排列對比。如圖9所示，隨著浮床相對間距的不斷增大，浮床上游左、中、右線垂線平均流速逐漸減小；浮床下游左、右線垂線平均流速基本不變，中線垂線平均流速逐漸減小。浮床上游左右線與中線垂線平均流速差值基本不隨著浮床相對間距變化，約為0.01 m/s；浮床下游左右線與中線垂線平均流速差值隨著浮床相對間距增大而增大。

圖9 浮床不同相對間距串聯排列工況垂線平均流速變化

（3）浮床不同間距交錯排列對比。如圖10所示，隨著浮床間距的不斷增大，浮床上游右線垂線平均流速基本保持不變，左線、中線垂線平均流速逐漸減小；浮床下游中線、右線垂線平均流速逐漸增大，左線垂線平均流速逐漸減小。上游左、右線差值隨著浮床間距增大而不斷增大，下游反之。

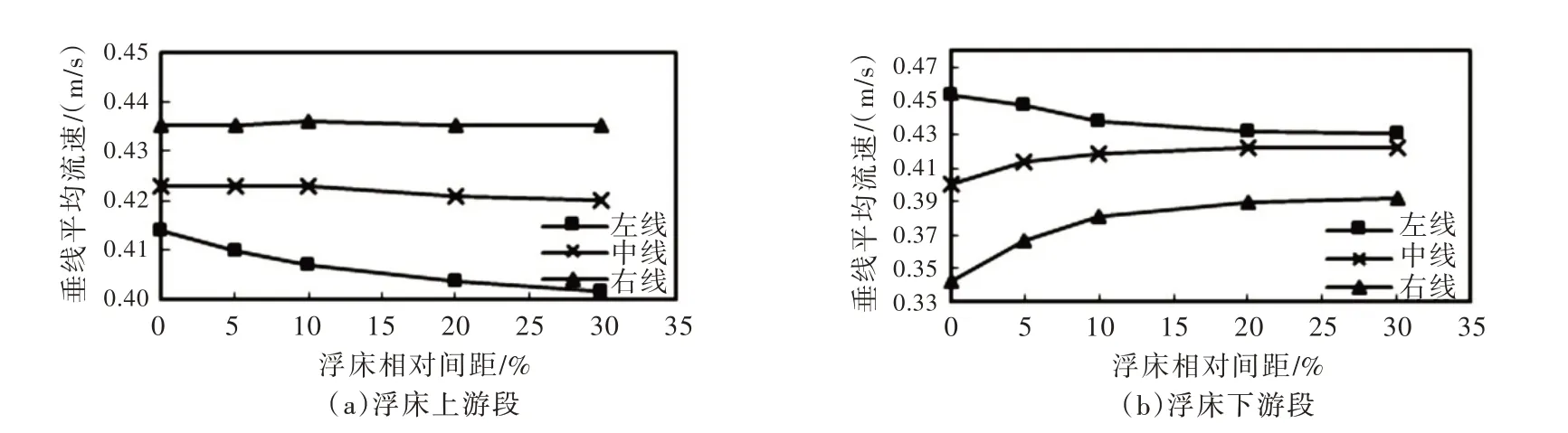
圖10 浮床不同相對間距串聯排列工況垂線平均流速變化

3.2.3 紊動能 無量綱化單位質量流體的時均紊動能可以根據下式進行計算：

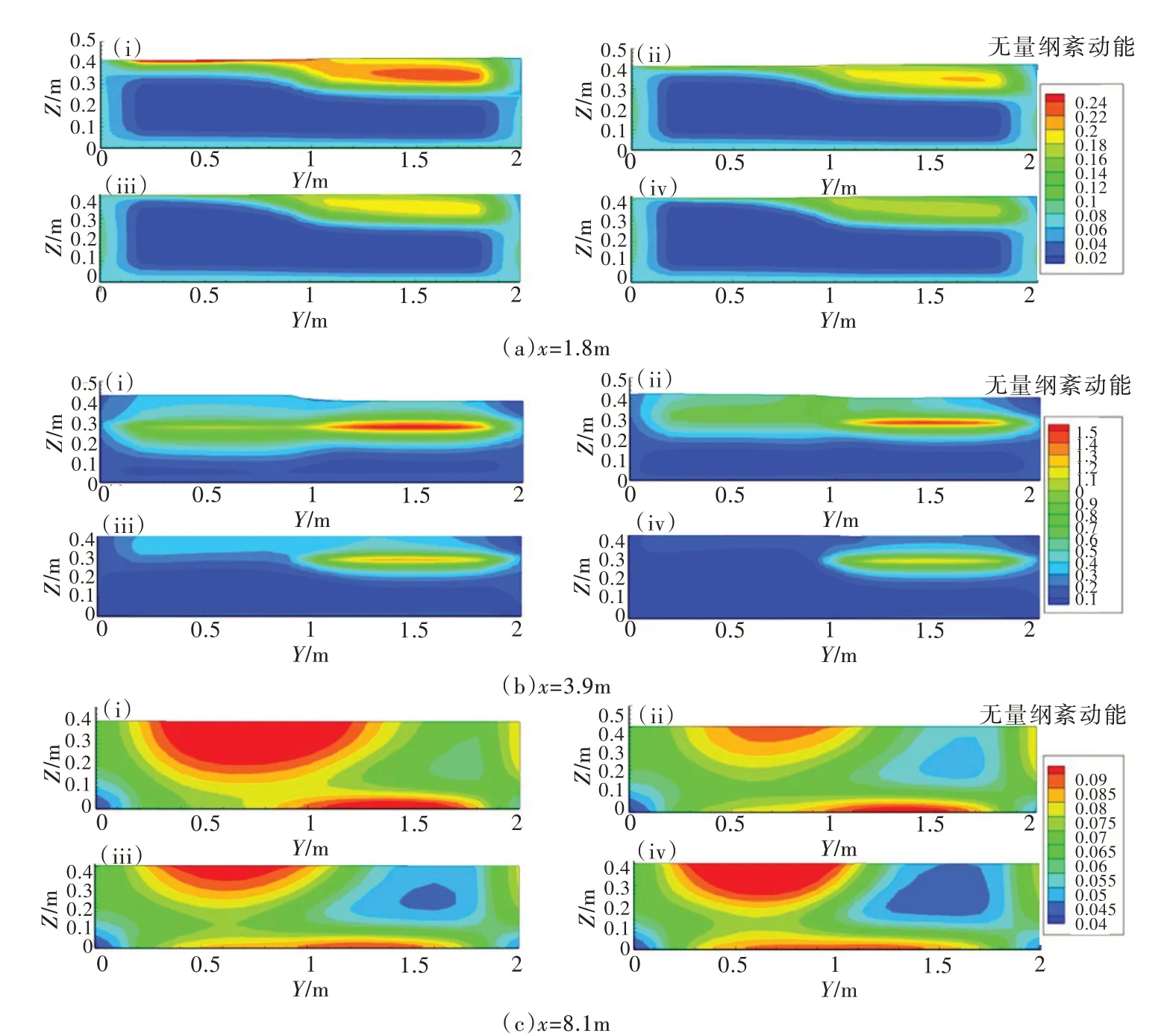
圖11 浮床交錯排列工況無量綱紊動能變化（（i）、（ii）、（iii）、（iv）分別為浮床間距為0、0.1、0.2、0.4m的工況）

3.3 討論

3.3.1 紊流計算中多孔介質處理方式及誤差分析 生態浮床的根系區域存在復雜的相互連通的微小空隙，且柔性的植物根須隨水流擺動，產生附加的紊動能與耗散，造成較大的阻力損失。目前，數值模擬時對植物根系區域存在多種概化方式，例如Cheng[19]等將規則排列的圓柱陣列模擬阻水植物，通過在動量守恒方程、紊流模型方程中增加阻力作用項，描述植物對水流的阻礙作用，合理反映植株與水流之間的相互作用。本文主要針對浮床對水流的阻礙及擾動作用展開研究，將生態浮床概化為兩層式固定多孔介質域上層為低透水性的浮床主體區，下層為高透水性的浮床根系區。多孔介質模型采用經驗公式計算多孔介質對流動產生的阻力，即在三維數學模型動量守恒方程上考慮動量消耗的源項，計算分別考慮了浮床主體區和根系區的紊動耗散。阻力系數運用實測資料率定，類似于Cheng[19]在動量方程、紊流模型方程中增加動量消耗項，反映植物對動水的擾動及其阻水效果；另一方面，生態浮床根系區概化為多孔介質域類似于植物剛性化，而柔性植株的綜合糙率小于剛性植株[20]。本文主要針對浮床對水流的阻礙及擾動作用展開研究，雖然將植物根系概化為多孔介質相較于考慮植被的柔性根系隨水流擺動的狀態對水流的阻礙及擾動作用偏大，但這并不會導致“不同布設方式的生態浮床對水流結構影響研究”成果規律性的改變，且計算結果偏安全。

3.3.2 工程應用中浮床排列方式的選擇 生態浮床在凈化水質的同時，會壅高水位，影響河流行洪排澇能力。本文通過對比研究發現相比于串聯排列，交錯排列浮床上游段水面壅高度更大。隨著浮床間距的不斷增大，串聯排列浮床上、下游水位相對壅高度均不斷增大，當相對間距大于50%時基本穩定；而交錯排列浮床上、下游水位相對壅高度均隨浮床間距的增大而減小，當相對間距大于20%時基本穩定。因此，從減小水位壅高角度，同密度生態浮床串聯排列優于交錯排列方式，但交錯排列一定程度上增加水流紊動強度，有利于污染物的吸收與擴散。

4 結論

本文利用一種兩層式固定多孔介質域概化生態浮床，構建生態浮床不同布設方式的水槽三維水動力數學模型并運用試驗資料率定計算參數驗證數學模型。對比浮床不同間距的串聯、交錯排列方式等14種工況的計算成果，研究不同布設方式的生態浮床對水流流速、水位、紊動能等水動力參數結構的影響。主要結論如下：（1）布設生態浮床后浮床上游水面壅高、下游水面先局部降低后恢復。浮床段垂線流速分布呈水面和底壁附近流速較小、中間流速較大的“紡錘形”且平均流速及紊動能增大。（2）相較于浮床串聯排列，交錯排列方式對水位、流速、紊動能等水動力參數的影響增大，且增大程度隨交錯排列的浮床間距的增大而減小，與浮床串聯排列相關變化趨勢相異。（3）實際應用中可結合研究成果優化生態浮床的布設方式，既避免水位壅高過大，又營造適中的水流紊動強度，有利于污染物吸收分散。