亞軌道飛行器返場技術(shù)研究

汪保旭，孫歌蘋

(南京航空航天大學 飛行控制研究所，江蘇 南京 210016)

0 引言

亞軌道飛行器(SRLV)是一種在亞軌道空間飛行、可重復使用的多用途飛行器。相比于軌道飛行器，亞軌道飛行器具有系統(tǒng)結(jié)構(gòu)、發(fā)射條件簡單、飛行成本低等特點，因而在軍事和民營領(lǐng)域，亞軌道飛行器已經(jīng)成為研究的熱點。

根據(jù)不同的飛行任務(wù)，亞軌道飛行器在上升段與結(jié)束時狀態(tài)差異巨大，高度的變化范圍為30 km～70 km ,速度的變化范圍為0.76 m/s～1.27 m/s。不同的初始返回狀態(tài)對應(yīng)不同的航程，制導系統(tǒng)需根據(jù)初始返回點的狀態(tài)判斷飛行器能否返回著陸場。

亞軌道飛行器返回階段通常分為3個階段：初期返回段、能量管理段和著陸段。X-34應(yīng)急返場方案[1]可推算飛行器在能量管理段入口飛行狀態(tài)，比較該狀態(tài)下可飛行的航程以及到各個著陸場的待飛距離，選擇合適的著陸場并返回。航天飛機的GRTLS(glide return to launch site)即滑翔返回發(fā)射場制導[2-3]是在上升飛行的前4 min內(nèi)因發(fā)動機故障無法正常入軌，實施應(yīng)急策略，使航天飛機進入能量管理段窗口，并最終返回預先設(shè)計的發(fā)射場。

由于亞軌道飛行器的初期返回段高度較高，空氣稀薄，氣壓低，雖然待飛距離可以由橫側(cè)向制導算法計算出，但縱向無法規(guī)劃高度和動壓剖面，因而無法根據(jù)初期返回點的能量狀態(tài)判斷飛行器的航程能力，進而判斷能否返場。

本文將初期返回段當作能量管理段的延伸，參考能量管理段的判斷方法[4]，設(shè)計制導參數(shù)迭代算法，分別通過調(diào)整初期返回段的迎角指令、航向校準圓柱(heading align column, HAC)位置和切換進場方式來判斷飛行器能否從最高點返回著陸場，最后進行實例仿真驗證。

1 質(zhì)點動力學方程

亞軌道飛行器初期返回段主要考慮縱向運動，忽略橫側(cè)向的影響。由于地球自轉(zhuǎn)引起的哥氏力、重力加速度變化較小，假定重力加速度為常數(shù)，忽略地球曲率，忽略自轉(zhuǎn)的影響，簡化后的質(zhì)點動力學方程為：

(1)

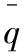
2 制導問題描述

根據(jù)不同的飛行任務(wù)，亞軌道飛行器從最高點返回時的狀態(tài)不同。高度越高，速度越大，飛行器的能量越大，可飛行的航程越遠，反之航程越近。因此，當初始返回點的位置、速度和高度確定時，制導系統(tǒng)就能夠判斷當前狀態(tài)能否返回著陸場。

參考能量管理段的判斷方法，速度一定時，由初始返回點到著陸場的待飛距離計算出高度指令。若當前高度小于高度指令，則飛行器到不了著陸場；若當前高度大于高度指令，則飛過著陸場。由上文知，無法單獨根據(jù)初期返回點的能量狀態(tài)判斷飛行器的航程能力，進而判斷能否返場。

初期返回段縱向制導采用的是跟蹤開環(huán)迎角指令，調(diào)整迎角指令可以改變初期返回段結(jié)束時的高度。另一方面，由于初期返回段的航程受迎角指令變化影響較小，因而調(diào)整返回段的待飛距離主要影響能量管理段后面的飛行階段。制導系統(tǒng)通過調(diào)整初期返回段的迎角指令和返回段的待飛距離來驗證給定狀態(tài)的飛行器能否返回著陸場。

3 迎角指令對高度的影響

在初期返回段，亞軌道飛行器的軌跡角為負，升力和阻力在縱向的分力豎直向上，平衡重力，從而降低垂直加速度，抑制下沉率[5]。下沉率的公式為：

(2)

式中V為空速。

(3)

式中：L為升力；D為阻力。

由于CL、CD是迎角α、馬赫數(shù)Ma和氣動舵面的函數(shù)，當馬赫數(shù)和氣動舵面一定時，迎角越大，CL、CD越大；升力越大，阻力越大，兩者豎直向上的合力越大。從而垂直加速度越小，下沉率變化越小，初期返回段結(jié)束時高度越高；反之，迎角越小，初期返回段結(jié)束時高度越低。

同一初始返回狀態(tài)，不同初始迎角條件下，圖1是初期返回段的航程變化曲線，圖2是下沉率變化曲線，圖3是高度變化曲線。可知，初期返回段航程受迎角指令變化的影響較小，下沉率和高度影響較大。

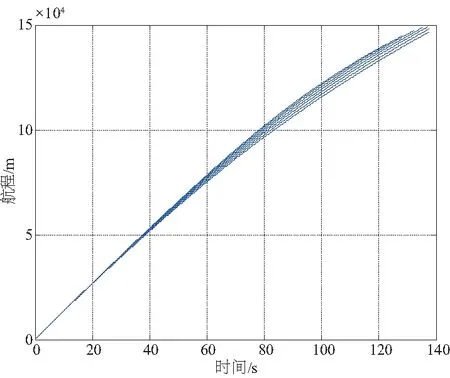
圖1 初期返回段航程變化曲線

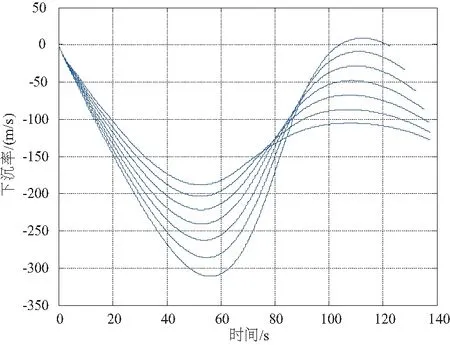
圖2 初期返回段下沉率變化曲線

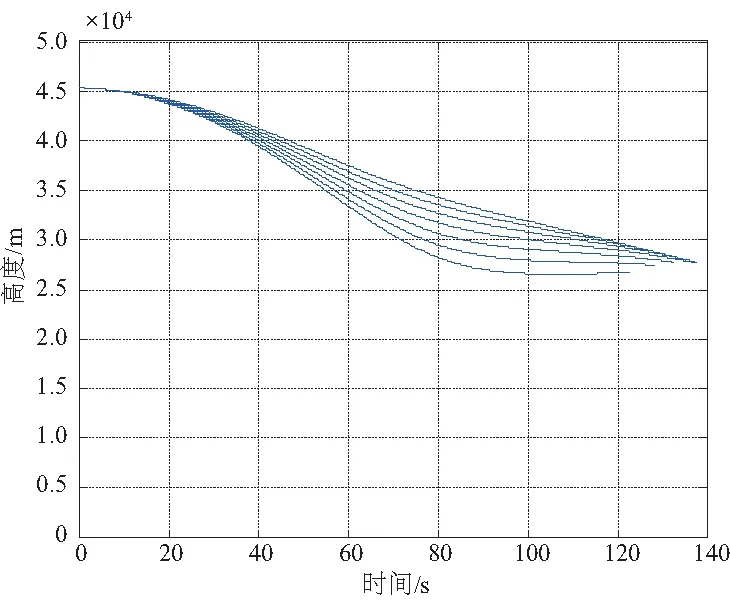
圖3 初期返回段高度變化曲線

4 調(diào)整待飛距離的影響

當初期返回段的迎角指令調(diào)整到邊界值時，再通過調(diào)整HAC位置和切換進場方式來改變整個返回段的待飛距離。

由第3節(jié)可知，初期返回段不同的迎角指令對航程影響不大，因而調(diào)整HAC的位置主要影響能量管理段后面的待飛距離。當初期返回段結(jié)束時，實際高度低于高度指令，將HAC調(diào)整到最小位置，減少待飛距離；反之，實際高度大于高度指令時，將進場方式由直接進場改為間接進場，增大待飛距離。由表1可知，HAC距離跑道越近，返回段的待飛距離越小，剩余的待飛距離越短，計算出的高度指令越低。圖4是進場方式示意圖，由圖可知，間接進廠的待飛距離遠，剩余飛行的距離多，計算出的高度指令高。

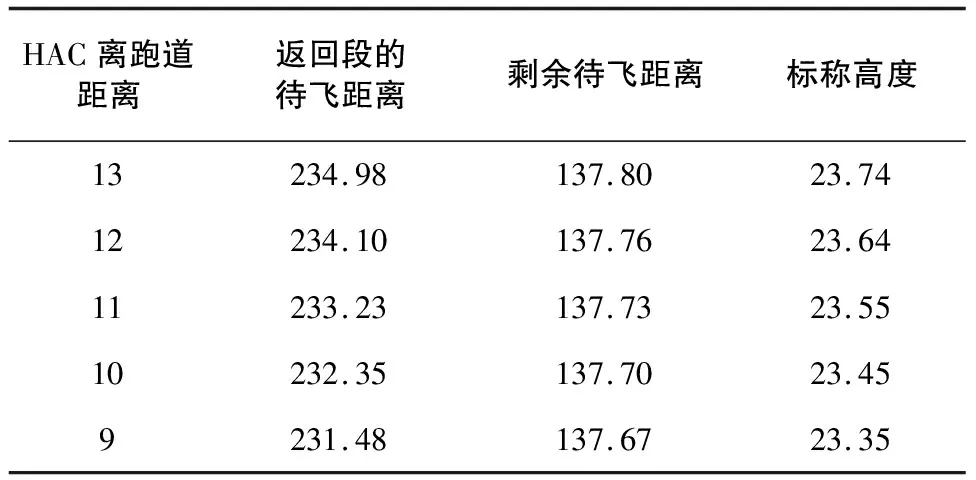
表1 初始返回點狀態(tài) 單位：km

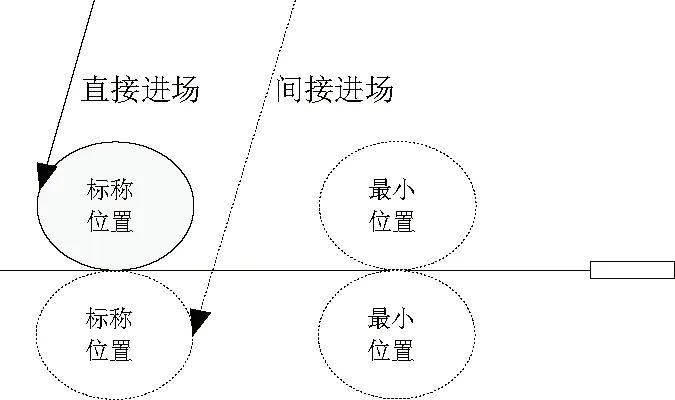
圖4 進場方式以及HAC位置示意圖

5 設(shè)計制導參數(shù)迭代算法

上文分別分析了RLV返回過程中，迎角指令對再入段結(jié)束時高度的影響以及調(diào)整HAC位置、切換進場方式對返回段待飛距離的影響。基于此，設(shè)計了制導參數(shù)迭代算法。

具體算法如下：任意給定一個初始返回狀態(tài)，首先初始化HAC和著陸機場，制導系統(tǒng)計算出到著陸場的待飛距離，并根據(jù)初始速度計算出迎角指令，接著進行時間迭代。當初期返回段結(jié)束時，可以得到初期返回段的航程，用總的待飛距離減去初期返回段的航程得到剩余的待飛距離。再由剩余的待飛距離插值出標稱高度指令，比較實際的高度和標稱高度，判斷能否返回著陸場。

當實際高度高于標稱高度時，能量過大，飛過著陸場，將初始迎角指令減少1°，進行時間迭代。再次判斷兩者的關(guān)系，若實際高度已經(jīng)小于標稱高度，或者實際高度比標稱高度僅高不到500 m，則該迎角指令可以滿足返場條件，飛行器可以返回著陸場；若實際高度還遠大于標稱高度，重復上步驟進行迎角迭代，直到迎角指令<16°時跳出迎角迭代(迎角指令下邊界取16°，上邊界取29°)。同樣，當實際高度小于標稱高度時，迎角反向迭代。

當迎角迭代到達邊界值時，進入調(diào)整待飛距離階段。當迎角指令迭代到16°時，實際高度依然遠大于標稱高度，切換進場方式為間接進場；當迎角指令迭代到29°時，實際高度依然小于標稱高度，調(diào)整HAC位置到最小位置。若實際高度與標稱高度之差依然>500 m，則飛行器無法返回著陸場，算法結(jié)束。軌跡迭代算法流程圖如圖5所示。

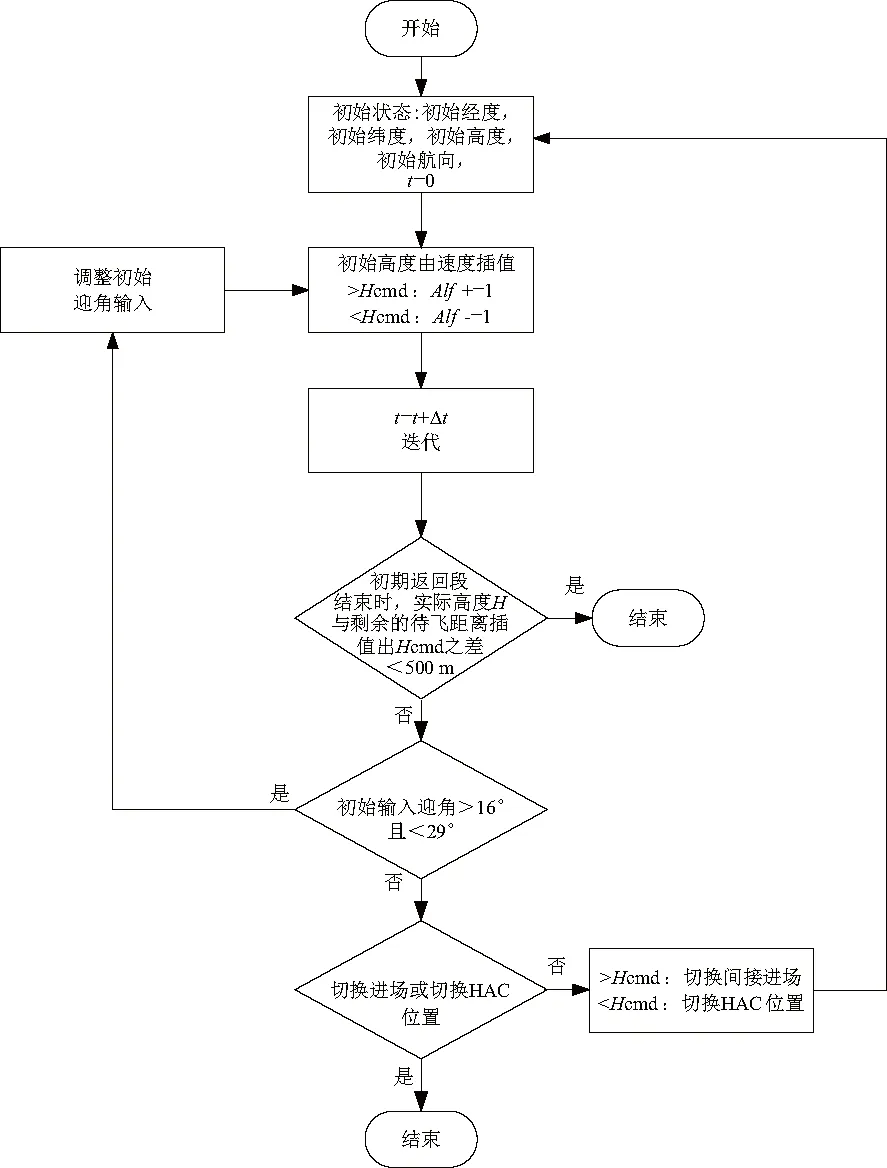
圖5 軌跡迭代算法流程圖

6 仿真實例驗證

給定3個初始返回狀態(tài)A、B、C，如表2所示，通過上述軌跡迭代算法判斷這3個不同的狀態(tài)能否返回著陸場。

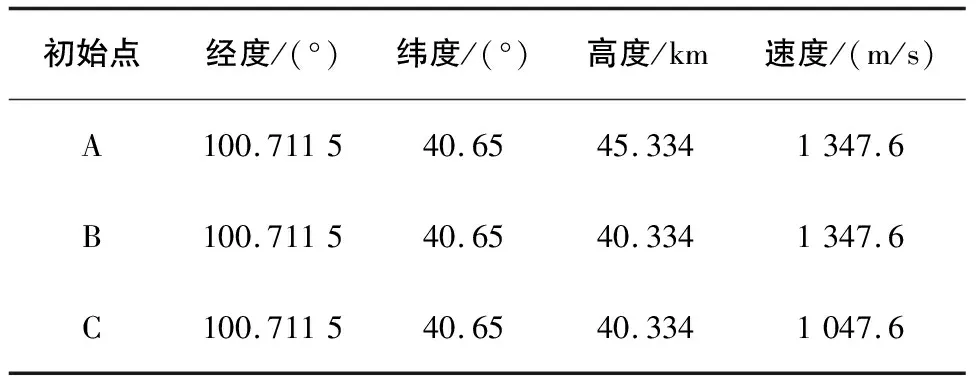
表2 初始返回點狀態(tài)

圖6是A點的返場狀況、圖7是B點的返場狀況、圖8是C點的返場狀況。藍色線是調(diào)整迎角指令時的狀態(tài)變化，綠色線是初期迎角指令一定，調(diào)整HAC位置的狀態(tài)變化，紅色線是最后一次軌跡迭代的結(jié)果。從圖6中可以看出，調(diào)整迎角和HAC位置可以顯著改變返場能力，但因為初始返回點高度、速度過大，初期返回段結(jié)束時，高度遠遠大于指令高度，因而在迎角指令和HAC位置的可調(diào)范圍內(nèi)，飛行器不能返回著陸場；相比較狀態(tài)A、狀態(tài)B初始高度降低，初期返回段結(jié)束時高度更低，由最后一條紅線所示，經(jīng)過迭代，飛行器正好可以返回著陸場(本刊為黑白印刷，如有疑問請咨詢作者)。

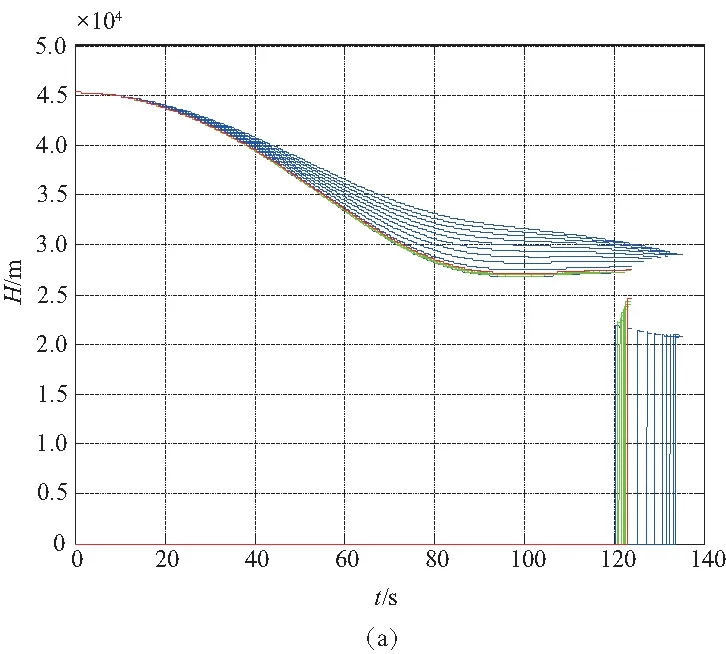
圖6 A點返場曲線

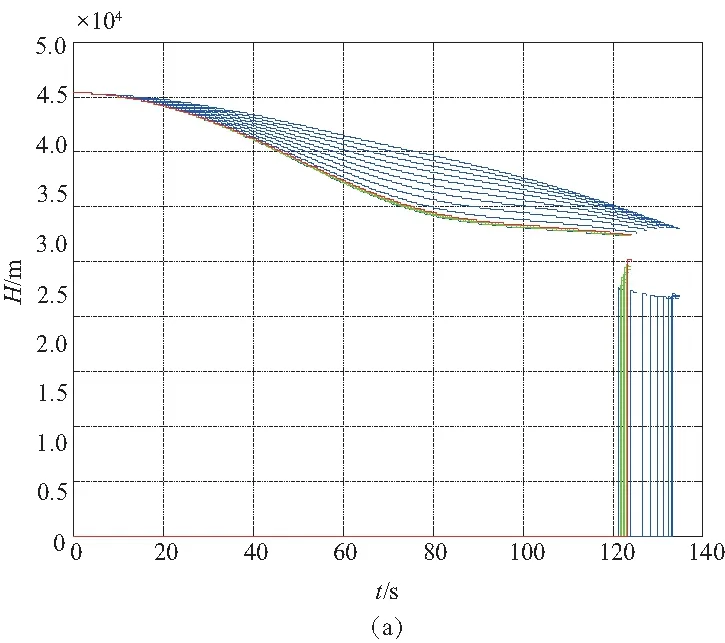
圖7 B點返場曲線

圖8 C點返場曲線

相比較狀態(tài)A和狀態(tài)B，狀態(tài)C的初始高度和速度均低，初期返回段結(jié)束時的高度明顯低于指令高度。由上文知，增大初期返回段的迎角指令，調(diào)近HAC的位置更低，經(jīng)過迭代，發(fā)現(xiàn)飛行器依舊不能返回著陸場。

7 結(jié)語

本文設(shè)計一種制導參數(shù)迭代算法，用來判斷亞軌道飛行器能否返回著陸場。由于初期返回段高度較高，空氣稀薄，氣壓低，制導系統(tǒng)縱向無法規(guī)劃高度和動壓剖面，無法根據(jù)初期返回點的能量狀態(tài)判斷飛行器的航程能力，進而判斷能否返場。通過調(diào)整初期返回段的迎角指令，調(diào)整HAC位置和切換進場方式改變待飛距離，在制導算法的迭代次數(shù)內(nèi)找到一組參數(shù)滿足高度的判斷條件，則當前狀態(tài)的飛行器能返回著陸場，否則算法結(jié)束迭代，不能返場。最后通過具體的實例驗證制導參數(shù)迭代算法的準確性。