基于Parareal算法的CIR模型數值保正性研究

查厚瀛 李永康 方澤來 師速利 李欣 劉翔

摘 要：CIR（Cox-Ingersoll-Ross）模型本身對數值算法具有保正性要求。因此，本文進行了隱式Euler方法作為粗細因子、Milstein方法作為粗細因子等四種不同組合的Parareal算法對CIR模型的數值計算，數值研究了Parareal算法在不同擾動值下的保正性及均方誤差收斂性。結果表明，上述考慮的Parareal算法具有均方收斂性和數值保正性。

關鍵詞：CIR模型? Parareal算法? 保正性? 收斂性

Research On the Numerical Positivity-Preserving of the CIR Model Based on the Parareal Algorithm

ZHA Houying*? LI Yongkang? FANG Zelai? SHI Suli? LI Xin? LIU Xiang

（School of Science， China University of Mining & Technology， Beijing， 100089 China）

Abstract：CIR （Cox-Ingersoll-Ross） model itself has the requirement of preserving the correctness of the numerical algorithm. Therefore， in this paper， Parareal algorithm with four different combinations of implicit Euler method as the thickness factor and Milstain method as the thickness factor is performed for the numerical calculation of CIR model， and the positivity-preserving properties and the convergence of the mean square error of Parareal algorithm under different disturbance values are numerically studied. The results show that the Parareal algorithm has mean square convergence and numerical positivity.

Key Words： Cox-Ingersoll-Ross （CIR） model; Parareal algorithm; Positivity-preserving properties; Astringency

1? CIR模型介紹

Cox、Ingersoll和Ross于1985年撰寫發布了兩篇論文[1，2]，提出了一個適用于簡單完整經濟體的具有時間連續特性的廣義均衡單因素模型，并將此模型應用于檢驗資產價格的實際應用中。他們在利率期限結構的基礎上進行深入研究，建立了Cox-Ingersoll-Ross模型，即CIR模型。CIR模型假設利率圍繞一個平均值在一定范圍內波動，其模型如下：

dX（t）=（θ_1-θ_2 X（t））dt+θ_3 √（X（t）） dω（t）? ? ? ? ? ? ? ?（1）

其中θ_1、θ_2、θ_3均為實常數，ω（t）表示Brown運動。由于CIR模型主要是描述短期利率的變化情況，而短期利率在現實中都是非負的，所以CIR模型需要嚴格保正。由（1）式不難看出，利率在均值μ附近上下波動，并以回復速率λ回復到均值μ，這說明CIR模型具有均值回復性。

近些年來，諸多學者進行了CIR模型的數值研究。蔡井偉、陳萍等學者用數值模擬和實證分析來驗證分段時變參數CIR模型進行利率，匯率建模的可行性和合理性[3];張連增、段白鴿兩位學者給出了CIR利率模型下永久年金現值變量的分布模擬[4];Wei利用最小二乘估計研究了離散觀測下的小對稱α穩定噪聲驅動的Cox-Ingersoll-Ross （ CIR ）模型的參數估計，得到了估計量的顯式表達式[5];Cheng等學者導出了多元CIR模型下債券定價方程的顯式擾動解，該計算方法對債券價格的評估是可行和準確的[6];Stamatiou等學者考慮了具有延遲和跳躍的均值回歸CIR/CEV過程作為金融市場的模型，證明上述模型解的非負性，并利用半離散方法提出了一個顯式保正數值格式，該格式在強意義下收斂于精確解[7];Yuan等學者分析一種基于分裂步方法的半解析數值算法及其在數學金融中的應用，將研究的算法與目前流行的一類基于Euler離散的數值格式進行了比較，比較了CIR模型下歐式看漲期權的準確性和計算時間與CIR模型下路徑依賴期權的收斂速度[8];Aghda等學者研究了CIR模型的平衡隱式方法（ BIM ），通過選擇合適的控制函數，BIM提供了數值解，保持了模型解的非負性，此外，給出了該方法數值解的p階矩有界性，并證明了方法的收斂性[9];Cen學者針對固定利率抵押貸款估值中的線性互補問題，給出了一個穩健的數值格式，在基本利率服從CIR模型的假設下，證明了該方法相對于利率幾乎是二階收斂的[10]。

2? Parareal算法

Parareal算法首先由Lions、Maday等人于2001年提出[11]。Turinici、Maday在2002年對Parareal算法做了進一步優化[12]。近些年，Parareal算法已經成為了研究比較廣泛的時間域并行算法，在確定性的微分方程研究中有諸多成果。但在隨機微分方程的研究中仍處于起步階段，還有諸多問題亟待解決。在目前的數值計算方面，國內的吳樹林、王志勇等學者對Parareal算法進行了理論研究[13]，證明了Parareal算法在有限時間區間內是超線性收斂，在無限時間區間內是線性收斂的，這使得Parareal算法可應用于更多計算問題。國內的張利英學者給出了基于Milstein格式的Parareal算法的收斂性分析[14]，并且針對具有弱阻尼和附加噪聲的隨機Schr?dinger方程，提出了一種基于指數θ-格式的Parareal算法[15]。Legoll等學者研究了通過Parareal算法對具有時間尺度離散的隨機微分方程的擬實計算以及數值收斂性研究[16]。Mayday等學者給出了一種Parareal算法的自適應變體，通過動態地提高細算法的精度，提升了算法的并行效率[17]。與其他并行算法相比，Parareal算法實現步驟簡單，并行效率高。該算法的主要思想為：將一個大的計算時間域劃分為若干個小的計算子區間，在整個時間域進行算法迭代的同時，也在子區間上進行迭代。這樣既保證了最終數值解的精度，也提升了算法的計算效率。以隨機微分方程（1）為例，給定初值后Parareal算法具體步驟如下：

步驟1：將整個計算域[0，T]以大步長ΔT對粗算法進行劃分，共劃為N個大區間[T_n，T_（n+1）]，n=0，1，...，N-1由數值算法G在每個時間點上計算得到粗網格的初值。

{█（X_（n+1）^（（0））=G（X_n^（（0）），ΔT），n=0，1，...，N-1@X_0^（（0））=X_0 ）┤? ? ? ? ? ? ? ?（2）

步驟2：通過細算法F將粗網格再進行劃分為細網格，即將大區間[T_n，T_（n+1）]以小步長Δt=ΔT/M一致劃為M等分，并在每個大區間的左端點上以數值算法F進行迭代。

{█（X ?_（n+（m+1）/M）^（（k））=F（X ?_（n+m/M）^（（k）），Δt），m=0，1，...，M-1@X ?_n^（（k））=X_n^（（k）） ）┤? ? ? ? ? ? （3）

步驟3：在大區間[T_n，T_（n+1）]上進行串行校正。

{█（X_（n+1）^（（k+1））=G（X_n^（（k+1）），ΔT）+F（X_n^（（k）），?t）-G（X_n^（（k）），ΔT），n=0，1，...，N-1@X_0^（（k+1））=X_0 ）┤? （4）

步驟4：判斷迭代結果是否符合終止條件，如果是，終止迭代;否則返回步驟2，直到滿足迭代收斂條件退出校正，并輸出結果。

3 CIR模型的數值保正性

基于CIR模型和Parareal算法，記粗算法為G，細算法為F，我們利用如下四種不同粗細算法得到了新的CIR模型的并行算法格式。

選取粗算法G為Milstein算法，細算法F為Milstein算法。

〖G：X〗_（n+1）=X_n+ΔT（θ_1-θ_2 X_n）+θ_3 √（X_n ） ω（T）+1/2 〖θ_3〗^2 √（X_n ）（〖ω（T）〗^2-ΔT）

〖F：X〗_（n+1）=X_n+Δt（θ_1-θ_2 X_n）+θ_3 √（X_n ） ω（t）+1/2 〖θ_3〗^2 √（X_n ）（〖ω（t）〗^2-Δt）

X_（n+1）^（（k+1））=X_n^（（k））+Δt（θ_1-θ_2 X_n^（（k）））+θ_3 √（X_n^（（k）） ） ω（t）+1/2 〖θ_3〗^2 √（X_n^（（k）） ）（〖ω（t）〗^2-Δt）

+〖（X〗_n^（（k+1））-X_n^（（k）））+ΔTθ_2 （X_n^（（k））-X_n^（（k+1）））+θ_3 （√（X_n^（（k+1）） ）-√（X_n^（（k）） ））ω（T）+1/2 〖θ_3〗^2 （√（X_n^（（k+1）） ）-√（X_n^（（k）） ））（〖ω（T）〗^2-ΔT）

選取粗算法G為隱Euler算法，細算法F為Milstein算法。

〖G：X〗_（n+1）=（X_n+ΔTθ_1+θ_3 √（X_n ） ω（T））/（1+θ_2 ΔT）

〖F：X〗_（n+1）=X_n+Δt（θ_1-θ_2 X_n）+θ_3 √（X_n ） ω（t）+1/2 〖θ_3〗^2 √（X_n ）（〖ω（t）〗^2-Δt）

X_（n+1）^（（k+1））=X_n^（（k））+Δt（θ_1-θ_2 X_n^（（k）））+θ_3 √（X_n^（（k）） ） ω（t）+1/2 〖θ_3〗^2 √（X_n^（（k）） ）（〖ω（t）〗^2-Δt）

+（〖（X〗_n^（（k+1））-X_n^（（k）））+θ_3 （√（X_n^（（k+1）） ）-√（X_n^（（k）） ））ω（T））/（1+θ_2 ΔT）

選取粗算法G為顯Euler算法，細算法F為隱Euler算法。

〖G：X〗_（n+1）=X_n+ΔT（θ_1-θ_2 X_n）+θ_3 √（X_n ） ω（T）

〖F：X〗_（n+1）=（X_n+Δtθ_1+θ_3 √（X_n ） ω（t））/（1+θ_2 Δt）

X_（n+1）^（（k+1））=（X_n^（（k））+Δtθ_1+θ_3 √（X_n^（（k）） ） ω（t））/（1+θ_2 Δt）+〖（X〗_n^（（k+1））-X_n^（（k）））+ΔTθ_2 （X_n^（（k））-X_n^（（k+1）））

+θ_3 （√（X_n^（（k+1）） ）-√（X_n^（（k）） ））ω（T）

選取粗算法G為隱Euler算法，細算法F為隱Euler算法。

〖G：X〗_（n+1）=（X_n+ΔTθ_1+θ_3 √（X_n ） ω（T））/（1+θ_2 ΔT）

〖F：X〗_（n+1）=（X_n+Δtθ_1+θ_3 √（X_n ） ω（t））/（1+θ_2 Δt）

X_（n+1）^（（k+1））=（X_n^（（k））+Δtθ_1+θ_3 √（X_n^（（k）） ） ω（t））/（1+θ_2 Δt）+（〖（X〗_n^（（k+1））-X_n^（（k）））+θ_3 （√（X_n^（（k+1）） ）-√（X_n^（（k）） ））ω（T））/（1+θ_2 ΔT）

本文中，選取粗細算法均為Milstein的格式，粗算法為隱Euler、細算法為Milstein的迭代格式、粗算法為顯Euler、細算法為隱Euler，以及粗細算法均為隱Euler的4種組合算法，對CIR模型的保正性和均方誤差收斂性進行研究。

4 模型保正性分析

為了使CIR模型數值解有實際意義，要求Parareal算法計算所得的數值解嚴格保正。以CIR模型（1）為例，對上述4種不同粗細算法組合的Parareal算法進行數值實驗。

取初值X_0=0.5，θ_1=2，θ_2=1，細步長〖Δt=2〗^（-9），粗步長ΔT=8Δt。分別計算在擾動值θ_3=0，0.1，0.01，0.001情況下Parareal算法的數值解，并分析其是否具有保正性。

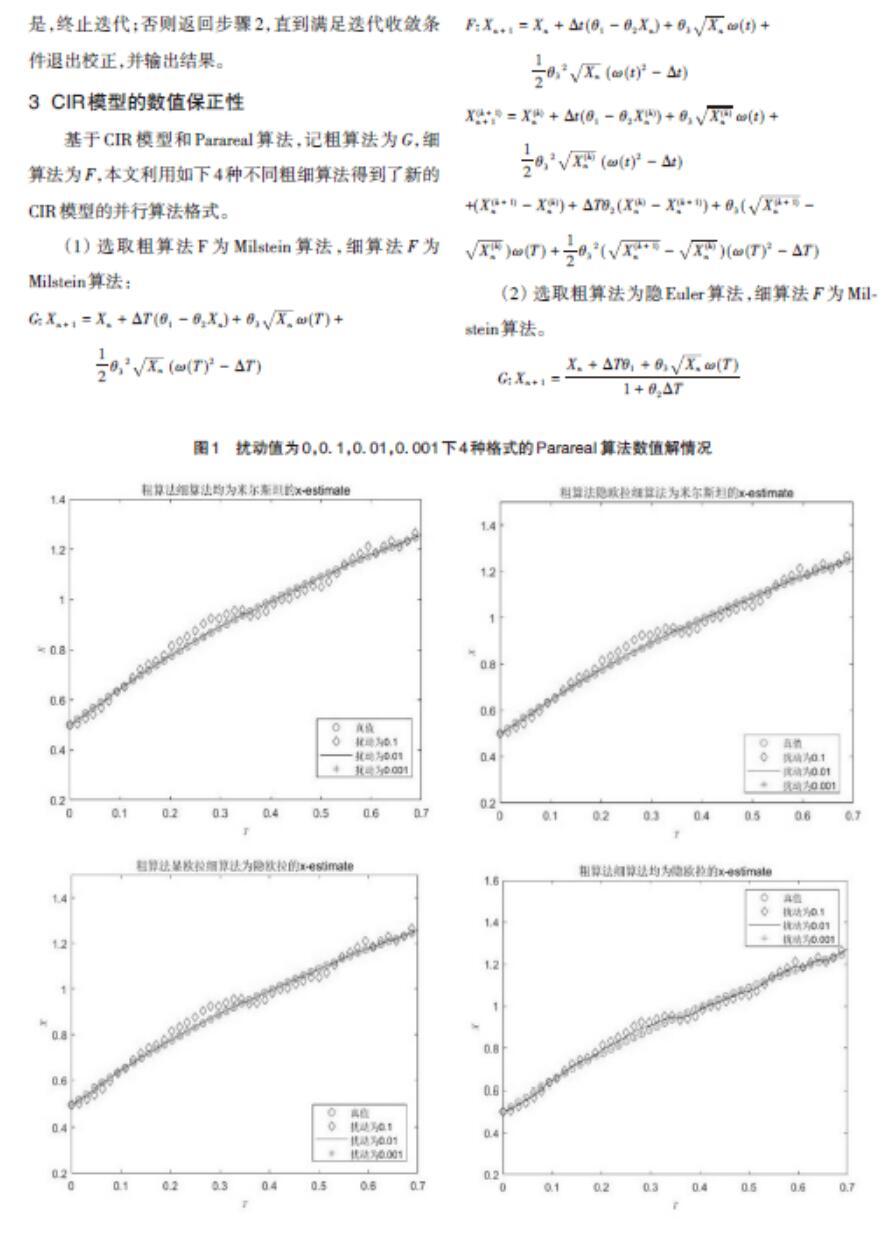
如圖1所示，橫軸表示粗步長，縱軸表示計算所得的數值解。在擾動值θ_3分別取0、0.1、0.01、0.001的情況下，均可觀察到數值解從0.5開始呈單調遞增趨勢，即上述四種不同粗細算子組合的Parareal算法均具有保正性。

5 均方誤差收斂性

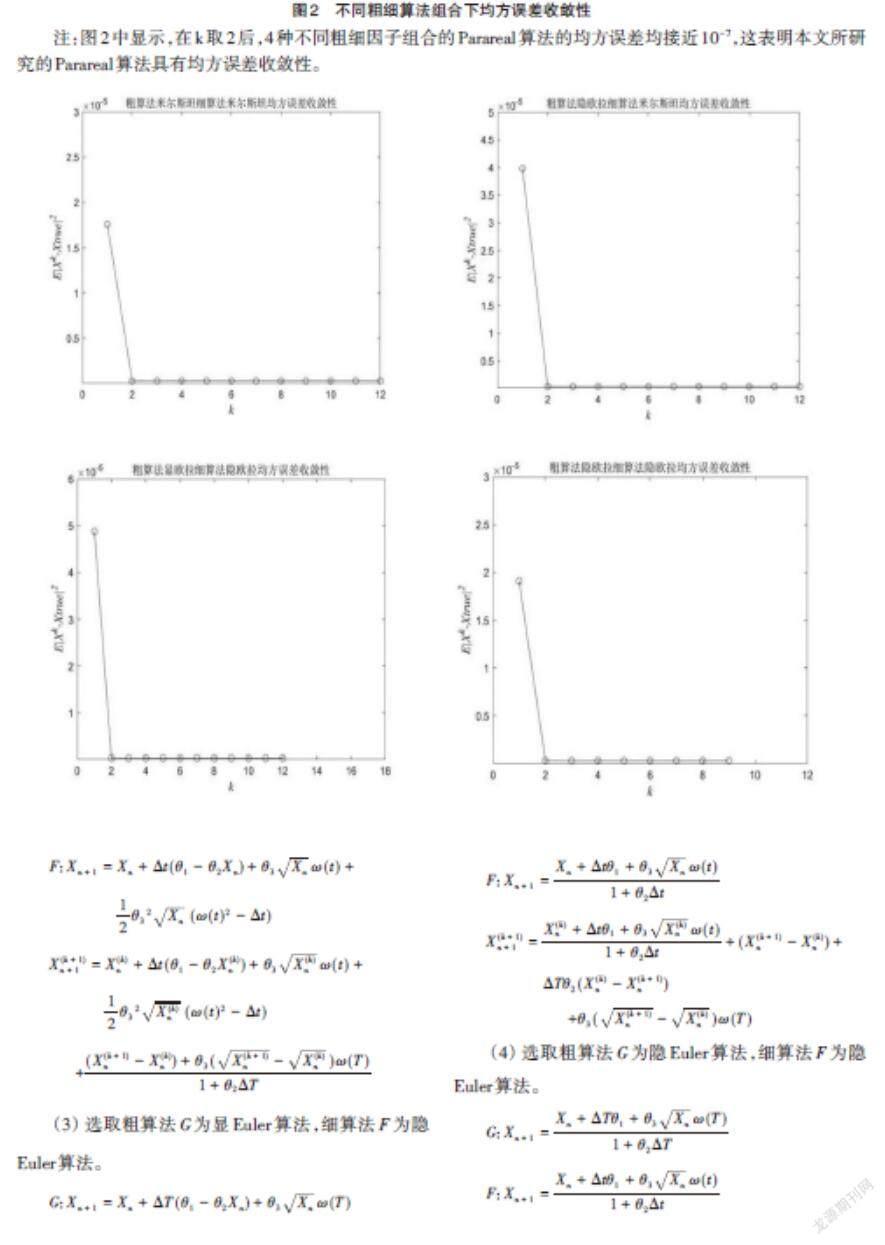
仍以（1）為例，取初值X_0=0.5，θ_1=2，θ_2=1，細步長〖Δt=2〗^（-9），粗步長ΔT=8Δt，精度為10^（-15），取100條軌道，在沒有擾動，即θ_3=0的情況下，真值可以計算為x_true=2-（3e^（-t））/2。應用上述4種不同粗細因子組合的Parareal算法求出數值解，計算數值解與真值的均方誤差supE（〖|X^k-X_true |〗^2），基于不同的粗細因子，得到如圖2所示結果。

圖2中顯示，在k取2后，4種不同粗細因子組合的Parareal算法的均方誤差均接近10^（-7），這表明本文所研究的Parareal算法具有均方誤差收斂性。

參考文獻

[1]John C. Cox，Jonathan E. Ingersoll，Stephen A. Ross. Abstract： A Theory of the Term Structure of Interest Rates and the Valuation of Interest-Dependent Claims[J]. Journal of Financial and Quantitative Analysis，1977，12（4）：385-407.

[2]John C. Cox，Jonathan E. Ingersoll，Stephen A. Ross. Duration and the Measurement of Basis Risk[J]. The Journal of Business，1979，52（1）：325-341.

[3]蔡井偉，陳萍，梅霞.分段時變參數CIR模型及其實證研究[J].數學的實踐與認識，2017，47（12）：76-83.

[4]張連增，段白鴿.CIR利率模型下永久年金現值變量的分布模擬[J].系統工程學報，2014，29（1）：56-65.

[5]Chao Wei. Estimation for the Discretely Observed Cox–Ingersoll–Ross Model Driven by Small Symmetrical Stable Noises[J]. Symmetry，2020，12（3）：3-9.

[6]Cheng-Hsun Wu. Perturbation solutions for bond-pricing equations under a multivariate CIR model with weak dependences[J]. Journal of Computational and Applied Mathematics，2019，361：208-213.

[7]I.S. Stamatiou. An explicit positivity preserving numerical scheme for CIR/CEV type delay models with jump[J]. Journal of Computational and Applied Mathematics，2019，360：83-97.

[8]Yuan Yuan. Non-Negativity Preserving Numerical Algorithms for Problems in Mathematical Finance[J]. Applied Mathematics，2018，9（3）：313-317.

[9]A.S. Fatemion Aghda，Seyed Mohammad Hosseini，Mahdieh Tahmasebi. Analysis of non-negativity and convergence of solution of the balanced implicit method for the delay Cox–Ingersoll–Ross model[J]. Applied Numerical Mathematics，2017，118：250-258.

[10]ZHONGDI CEN. ROBUST NUMERICAL SCHEME FOR A FIXED-RATE MORTGAGE VALUATION MODEL UNDER CIR INTEREST RATES[J]. Asian Journal of Mathematics and Computer Research，2016，11（2）：281-288.

[11]Lions Jacques Louis，Maday Yvon，Turinici Gabriel. A “Parareal” in time discretization of PDE"s[J]. Comptes Rendus de l"Academie des Sciences Series I Mathematics，2000，332（7）：381-390.

[12]Yvon Maday，Gabriel Turinici. A Parareal in time procedure for the control of partial differential equations[J]. Comptes rendus - Mathématique，2002，335（4）：387-392.

[13]吳樹林，王志勇，黃乘明.Parareal算法的均方穩定性分析[J].計算數學，2011，33（2）：113-124.

[14]L. Zhang， J. Wang， W. Zhou， et al.Convergence analysis of parareal algorithm based on Milstein scheme for stochastic differential equations[J]. Comput. Math.， 2020，38（3）： 487-501.

[15]J. Hong， X. Wang， L. Zhang. Parareal exponential θ-scheme for stochastic Schr?dinger equations with weak damping and additive noises， SIAM[J]. Sci. Comput.，2019，41（6）：B1155–B1177.

[16]Frédéric Legoll， Tony Lelièvre， Keith Myerscoughet， et al.Parareal computation of stochastic differential equations with time-scale separation： a numerical convergence study[J].Computing and Visualization in Science，2020，23（1-4）：172-182.

[17]Y. Maday， O. Mula.An adaptive parareal algorithm[J].Journal of Computational and Applied Mathematics，2020，377：3-15.

通信作者：查厚瀛（2000—），女，本科在讀，研究方向：統計學。? ? ?Email：1749775495@qq.com。

基金項目：本項目由北京市大學生創新訓練項目資助（項目編號：202011413190）。