UWB 測距室內定位算法誤差分析

張 媛，繆相林，王 梅，丁 凰

（1.西安交通大學 城市學院，西安 710018；2.西安交通大學 計算機科學與技術學院，西安 710049）

0 引言

如今，室外定位系統已經發展的非常成熟，如美國的全球定位系統（global position system, GPS）[1]、我國的北斗衛星導航系統（BeiDou navigation satellite system, BDS）以及歐盟的伽利略衛星導航系統（Galileo satellite navigation system, GSNS）。這些定位系統在室外具有較準確的定位性能，但是它們在室內環境下，則無法完成定位。而現今，室內定位已成為傳感網絡的最主要的議題[2-4]。

為了提高室內定位精度，研究人員提出了一些局部定位系統（local positioning system, LPS）。例如：文獻[5]將無線保真（wireless fidelity, WiFi）定位技術應用到復雜的室內環境中；文獻[6-7]采用射頻識別（radio frequency identification, RFID）標簽進行室內定位。盡管基于WiFi 和RFID 的LPS技術已經在室內環境中廣泛使用，但是它們只能提供米級的定位精度。

為了獲取更高的定位精度，研究人員把目光投向超寬帶（ultra wide band, UWB）技術。例如，文獻[8]利用UWB 技術跟蹤室內環境的目標。UWB信號頻帶寬范圍為3.1～10.6 GHz，寬的頻帶性能使其具有極窄的脈沖，時間分辨率高，穿透性強，適合室內環境定位。此外，相比于其他技術，UWB 技術的功耗也小。

目前，研究人員針對UWB 定位系統，提出了不同的定位算法。例如：文獻[9]提出了融合UWB測距信息的室外高精度定位算法，根據車輛行駛航跡，并結合UWB 測距信息估計車輛位置。文獻[10]提出了改進雙向測距到達時間差定位算法的超寬帶定位系統，利用雙向測距并通過線性處理，提高定位精度。通常，基于UWB 定位算法，首先利用UWB 測距，然后再利用這些測距值，并結合定位算法估計節點位置。這些算法包括線性最小均方誤差估計（linearized least square estimation,LLSE）、指紋估計（finger print estimation, FPE）、加權質心估計（weighted centroid estimation, WCE）等。

這些定位算法的定位特性存在差異，在不同的環境下，定位性能并不相同。為此，本文在考慮視距（lineof-sight, LOS）和非視距（non-line-of-sight, NLOS）場景下，對LLSE、FPE 和WCE 的定位算法的特性（包括定位精度和算法的復雜度）進行分析計算。

1 基于UWB 的定位模型

圖1 為基于UWB 的室內定位模型。將錨節點（reference node, RN）部署在已知坐標值的固定位置上，測量RN 的信號到達盲節點（blind node, BN）的時間（time of arrival, TOA），并用測距方程將TOA 轉化為距離。然后將距離信息作為定位算法（LLSE、FPE 和WCE）的輸入，最終得到盲節點位置的估計值。

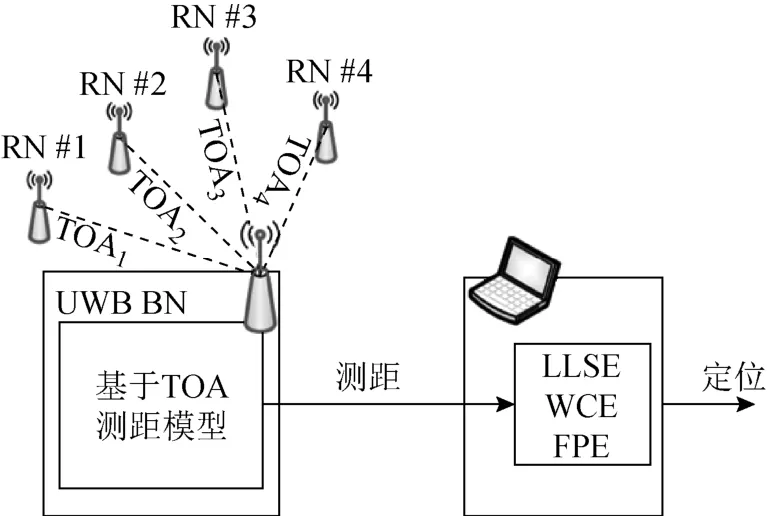
圖1 基于UWB 的定位模型

2 定位算法

2.1 線性最小均方誤差估計（LLSE）算法

LLSE 屬于UWB 室內定位算法中最簡單的1 種。通過最小化觀測數據間的均方誤差[11]來估計節點位置。令 di為盲節點離第i 個錨節點間的距離[12]，其定義為

式中： p =( xp,yp)為標簽位置；pi=( xi,yi)為第i 個錨節點位置。對式(1)進行平方、簡化處理后可得

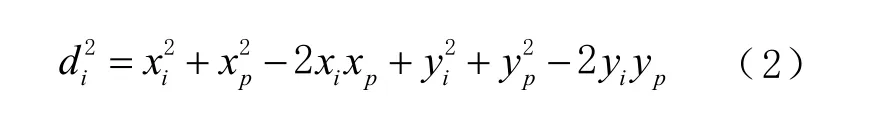
若有N 個錨節點，即 i =1, 2,… , N，可建立N 個等式。例如，第N 個等式為

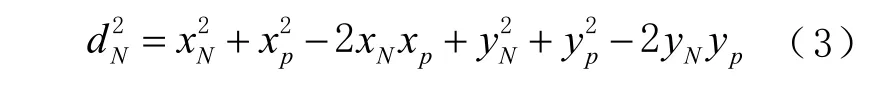
將式（2）與式（3）相減可得

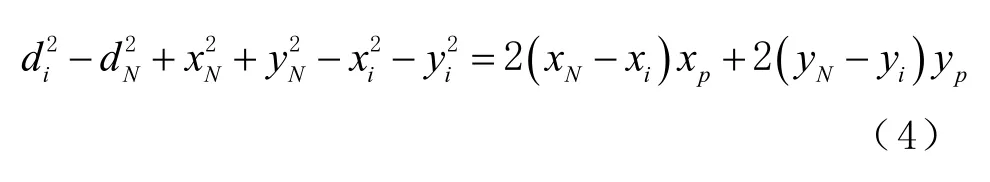
將N-1 個等式減去第N 個等式，再以矩形形式表述為

式中：b 為( N－ 1) ×1維矩陣； p 為 2 ×1維矩陣；A為(N－ 1)×2 維矩陣，它們的定義為

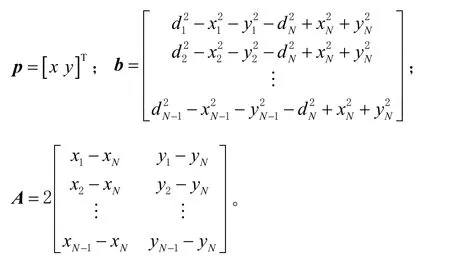
若A 不是方矩陣，就利用偽逆矩陣估計節點位置[13]為

2.2 加權質心估計（WCE）算法

WCE 的算法先估計盲節點到錨節點的距離d，再依據這些錨節點位置和距離估計盲節點位置。

具體而言，令( x1,y1),( x2, y2),…,( xN, yN)表示這N 個錨節點的位置，1d , d2,…,dN表示這些錨節點離盲節點的距離，則盲節點的位置坐標（x,y）為

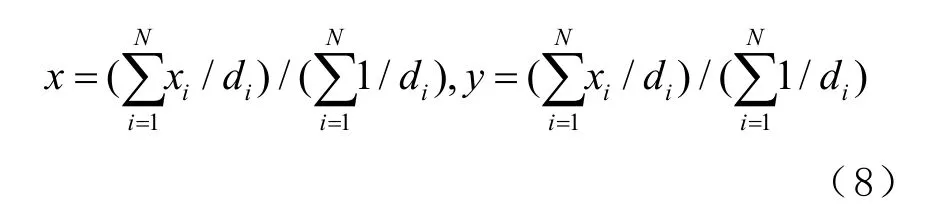
式中：i 表示錨節點的索引號；ix 表示第i 個錨節點的橫坐標；yi表示第i 個錨節點的縱坐標。

盲節點根據距離遠近選出與其最近的4 個錨節點，再利用這4 個錨節點位置即可出估計盲節點的位置。

2.3 指紋估計（FPE）算法

FPE 算法是基于UWB 測距的室內定位最常用的算法。先構建錨節點與盲節點間距離的指紋匹配圖，然后計算當前距離，進而估計盲節點的位置。

具體而言，FPE 算法可分為離線采集和在線匹配2 個階段，如圖2 所示。

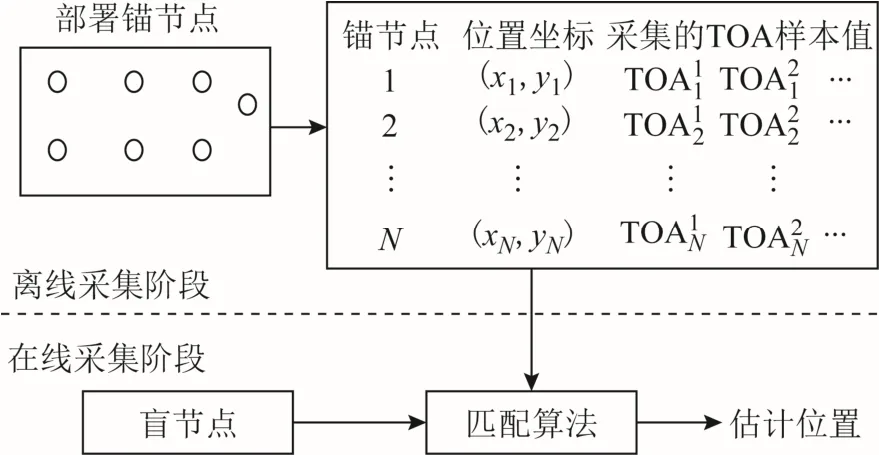
圖2 指紋估計模型

在離線采集階段，部署錨節點，并獲取錨節點在各點位置的TOA 值，即將每個位置坐標信息和相應的TOA 值構成1 條信息鏈，形成1 條指紋。在在線匹配階段，估計盲節點所接收的TOA 值，再與數據庫里的指紋進行匹配，找到匹配度最高的位置作為盲節點位置。

令 fj表示存儲在數據庫的距離測量值，其定義為

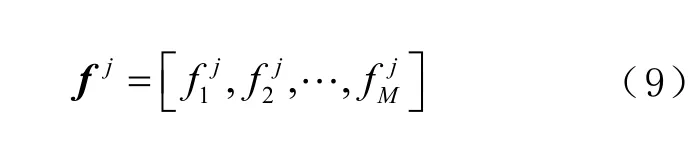
式中M 為測量次數。

假定盲節點離錨節點的距離矢量為

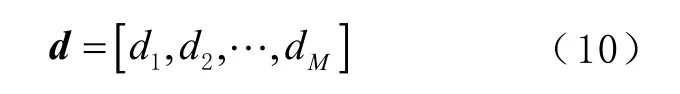
再將 fj與d 進行比較，并將具有最小距離的位置點作為盲節點位置，即

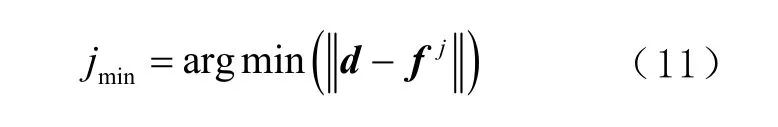
盲節點位置的估計值為

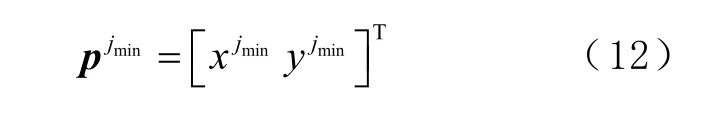
3 性能分析

為了更好地分析LLSE、WCE 和FPE 算法的性能，利用矩陣實驗室（MATLAB）R2016a 軟件建立仿真平臺。考慮LOS 和NLOS 2 個場景。在2 維 100 m× 120 m 仿真區域內部署5 個錨節點和10 個盲節點，且以隨機方式部署這些盲節點。10 個盲節點的真實位置如表1 所示。

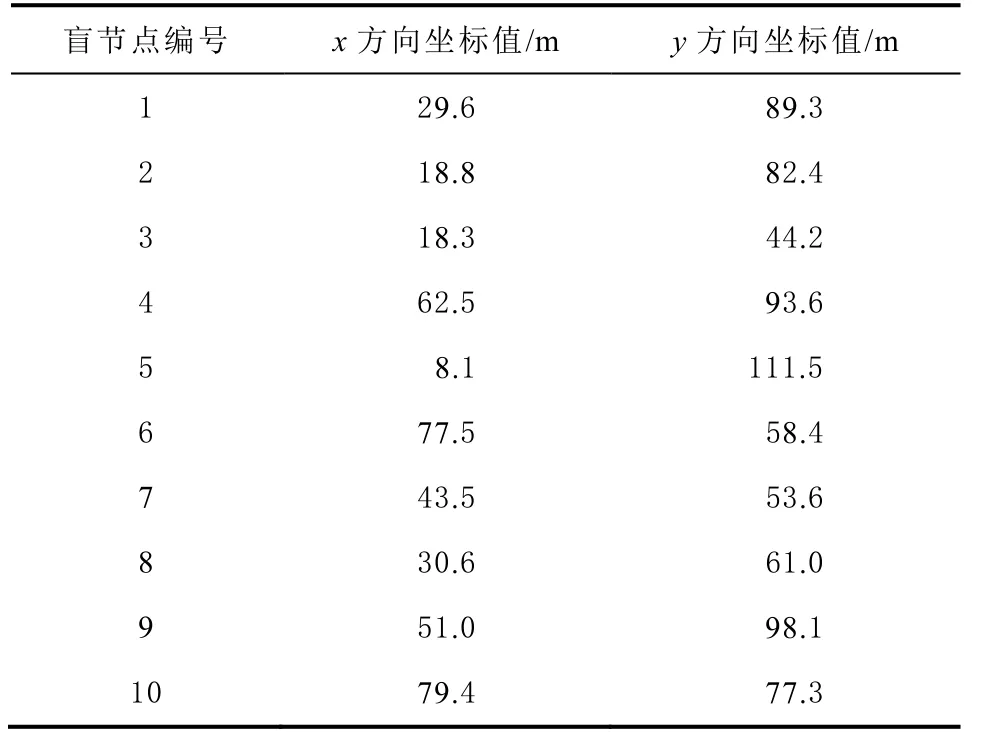
表1 10 個盲節點的真實位置

先利用圖1 流程建立模型測距，再利用LLSE、WCE 和FPE 算法估計盲節點位置。此外，在以下仿真圖中：實黑圓點表示錨節點位置；三角形表示盲節點的真實位置；空心圓點表示算法估計的盲節點位置。

3.1 LOS 場景

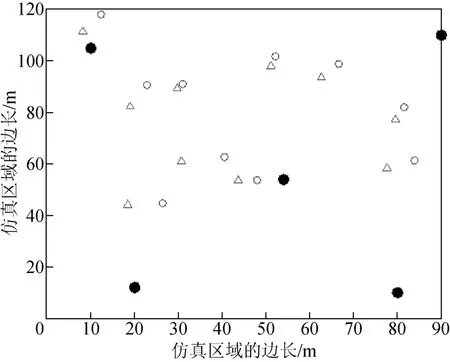
圖3 LLSE 算法對盲節點的位置估計（LOS 場景）

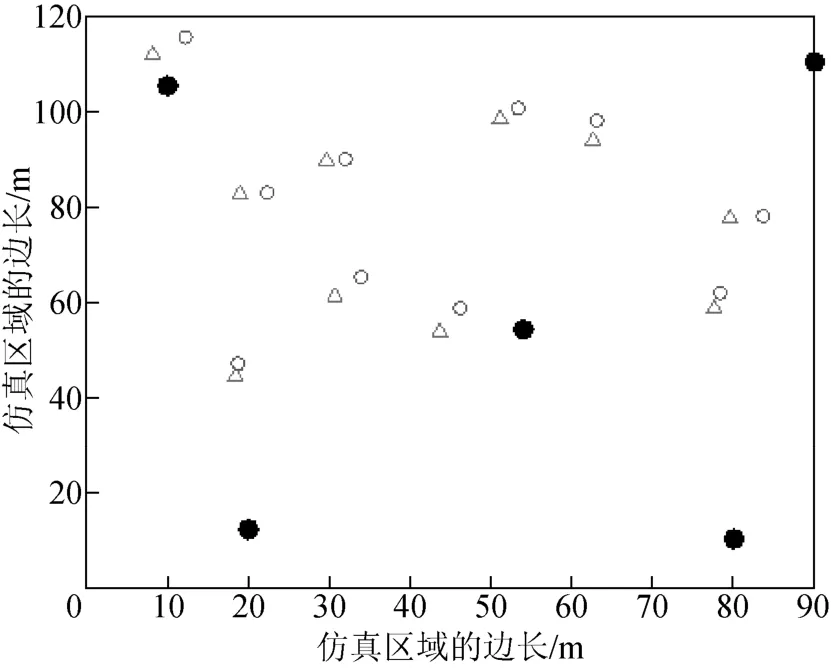
圖4 WCE 算法對盲節點的位置估計（LOS 場景）

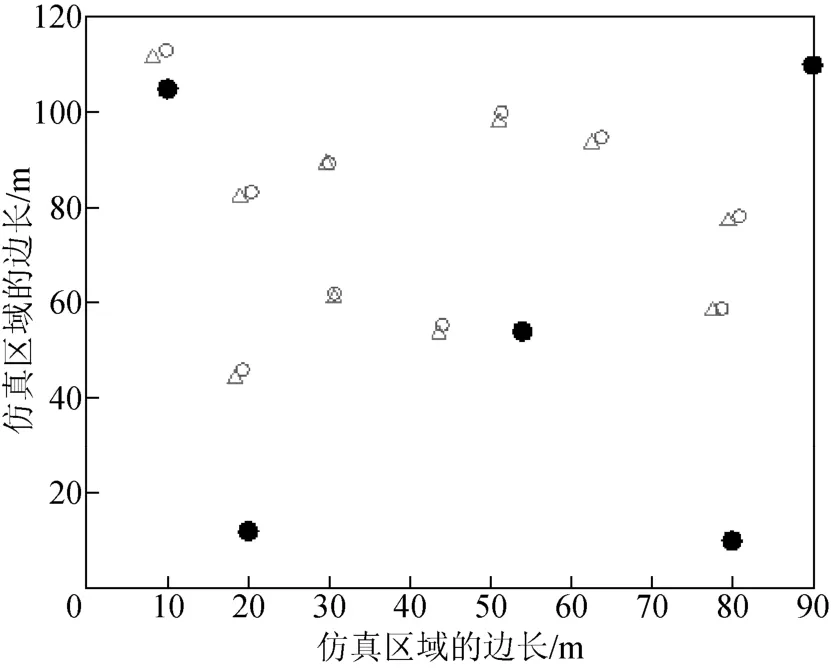
圖5 FPE 算法對盲節點的位置估計（LOS 場景）

圖3 ～圖5 分別顯示了LLSE、WCE 和FPE 算法對盲節點的位置估計，圖中的橫、縱坐標分別表示2 維區域長和寬。

從圖3～圖5 可知：相比于LLSE 和WCE，FPE算法能夠準確估計盲節點的位置；LLSE 算法的估計誤差最大；FPE 算法的均方誤差為0.657 4 m；LLSE 算法和WCE 算法的均方誤差分別為0.871 2 和0.723 4 m。

表2 為3 種算法的定位精度及復雜度程度。從表2 可以看出，FPE 算法的運行時間最多，這也說明FPE 算法的復雜度高，是以高的復雜度換取高的定位精度。

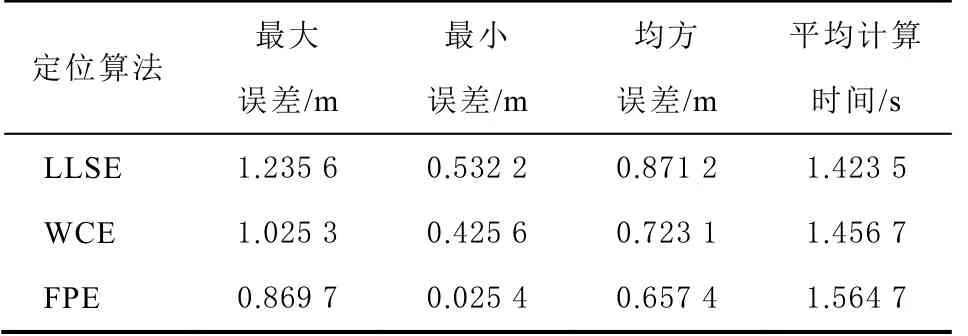
表2 LLSE、WCE 和FPE 算法的定位及復雜度性能（LOS 場景）

3.2 NLOS 場景

本小節分析3 個定位算法在NLOS 場景中的定位特性。圖6～圖8 顯示了LLSE、WCE 和FPE算法的定位特性。

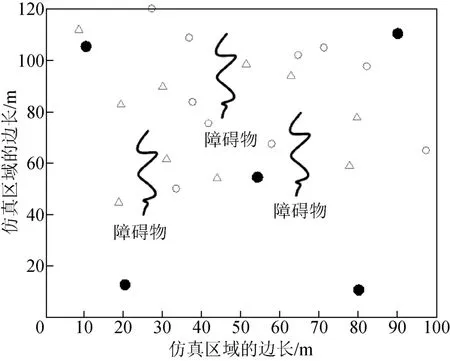
圖6 LLSE 算法對盲節點的位置估計（NLOS 場景）

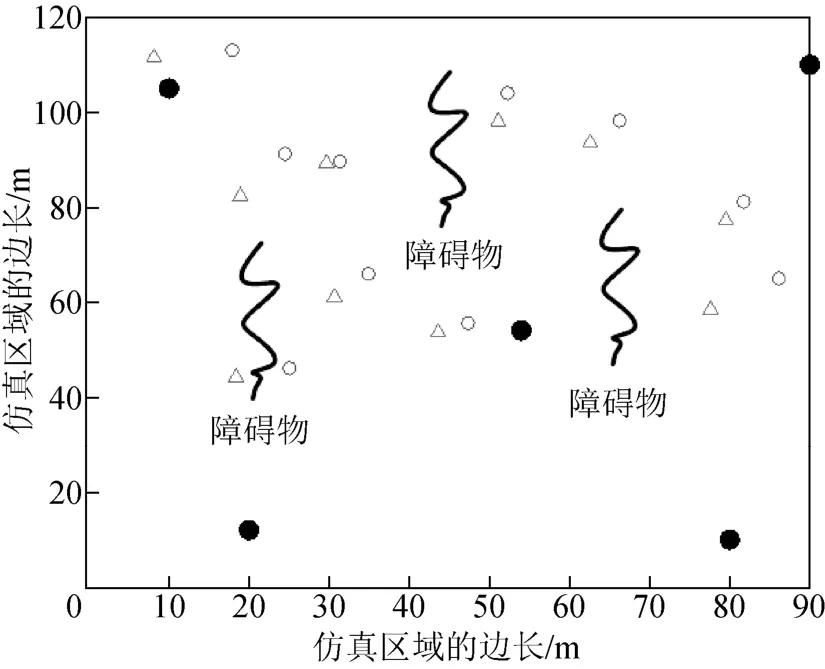
圖7 WCE 算法對盲節點的位置估計（NLOS 場景）

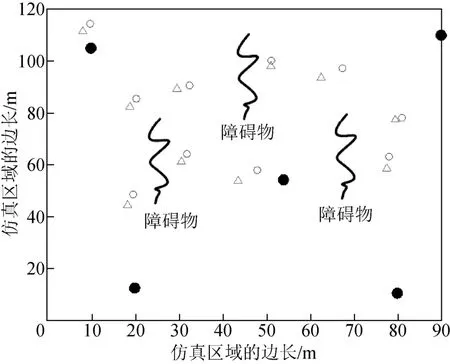
圖8 FPE 算法對盲節點的位置估計（NLOS 場景）

正如預期的那樣，相比于LOS 場景，NLOS 場景下的定位精度下降。原因在于：NLOS 場景中的障礙物阻礙了信號傳輸，擾動了對信號的TOA 測量，加大了測距誤差，最終降低了定位精度。此外，相比于LLSE 和WCE 算法，FPE 算法仍具有高的定位精度。

表3 表示了3 個算法在NLOS 場景下的定位精度及運算時間。對比表2 和表3 內數據可知，NLOS 場景下的定位誤差較差，例如，LLSE 算法在LOS 場景下的均方誤差為0.871 2 m，而在NLOS 場景下的均方誤差達到1.230 3 m。但各算法在LOS 和NLOS 2 個場景下運算時間并沒有多大變化。

表3 LLSE、WCE 和FPE 算法的定位及復雜度特性（LOS 場景）

4 結束語

本文針對基于UWB 測距的室內定位算法進行分析，分析了在NLOS 和LOS 2 個場景下，LLSE、WCE 和FPE 算法的均方誤差和復雜度。實驗數據表明，相比于LLSE 和WCE，FPE 算法具有更低的定位誤差，但復雜度較高。此外，NLOS 場景對定位有負面影響。相比于LOS 場景，NLOS 場景下的定位精度有所下降。