基于模糊PID的水下金剛石繩鋸機張緊力控制策略研究

徐田豐楊 啟

(1.上海交通大學 海洋工程國家重點實驗室，上海200240；2.上海交通大學 高新船舶與深海開發(fā)裝備協(xié)同創(chuàng)新中心，上海 200240；3.上海交通大學海洋水下工程科學研究院有限公司，上海200231)

0 引 言

近年來，海洋工程產(chǎn)業(yè)規(guī)模不斷擴大，海洋油氣資源的開發(fā)利用也迅速發(fā)展，為國家能源供給提供了重要保障。隨著海洋油氣田的不斷開發(fā)與發(fā)展，很多使用年限較長的海底石油管道與導管架平臺逐步被廢棄，需要通過水下切割作業(yè)進行拆除。在各類切割方法中，水下金剛石繩鋸機憑借環(huán)保清潔、對環(huán)境要求低等特點，成為國內(nèi)外研究與發(fā)展的熱點。上海交通大學針對勝利油田導管架平臺拆除問題，研制了水下金剛石繩鋸機樣機，并開展了大量的切割試驗研究[1]。除了廢棄樁基的拆除，金剛石繩鋸機還被應用于海底裝備維修、打撈等海洋工程領域，2000年，在俄羅斯庫爾斯克號核潛艇的打撈工作中，采用金剛石繩鋸機完成了艇體外殼的分割作業(yè)[2]。

水下金剛石繩鋸機是一種柔性切割工具，在切削過程中，切割平臺在行進系統(tǒng)的推動下朝被切工件移動，通過金剛石切割鏈高速轉動對工件進行磨削，完成切割作業(yè)。切割鏈張緊力與磨削力密切相關，過小的張緊力會使切削工件速度較慢，效率低下；而過大的張緊力則會加快金剛石串珠的磨損，甚至造成切割鏈繃斷的風險。因此關于切削過程中切割鏈張緊力控制策略的研究對于提高切削效率具有重要意義。張永銳等通過金剛石繩鋸切削海底管道效率試驗得到串珠繩張緊力與切削壓力的關系曲線[3]。王海波等進行金剛石繩鋸切割管道的正交試驗，對切割過程中串珠繩張緊力與其他切削參數(shù)進行了優(yōu)化與協(xié)調[4]。Wu等針對金剛石線切割鋸繩張力控制提出了一種PI(比例積分)控制方法[5]。

本文針對水下金剛石繩鋸切削過程進行動力學建模，構建切割系統(tǒng)狀態(tài)空間方程，進而提出一種基于模糊PID的切割鏈張力控制策略。通過仿真試驗，驗證了該策略的魯棒性與動態(tài)性能。

1 水下金剛石繩鋸切割動力學分析

1.1 切割系統(tǒng)動力學模型

常見的水下金剛石繩鋸機本體結構如圖1所示，主要由切割裝置(包括切割鏈與切割滑輪)、行走裝置、夾緊裝置以及上下平臺結構等部分組成。從事切割作業(yè)時，母船在預定海域將金剛石繩鋸機下放到水中，經(jīng)由潛水員的輔助將夾緊裝置固定在海底石油管道、導管架平臺等目標上。母船通過臍帶纜等裝置與繩鋸機相連，進而控制切割過程。

水下金剛石繩鋸切割系統(tǒng)的簡化動力學模型如圖2所示，其中，輪1與輪2為可調整從動輪，輪3與輪4為主動切割輪，主動切割輪參數(shù)相同，可輸出同樣大小的驅動力矩。

考慮到工程實際情況，在建立水下金剛石繩鋸切割動力學模型之前，對其做出以下假設：

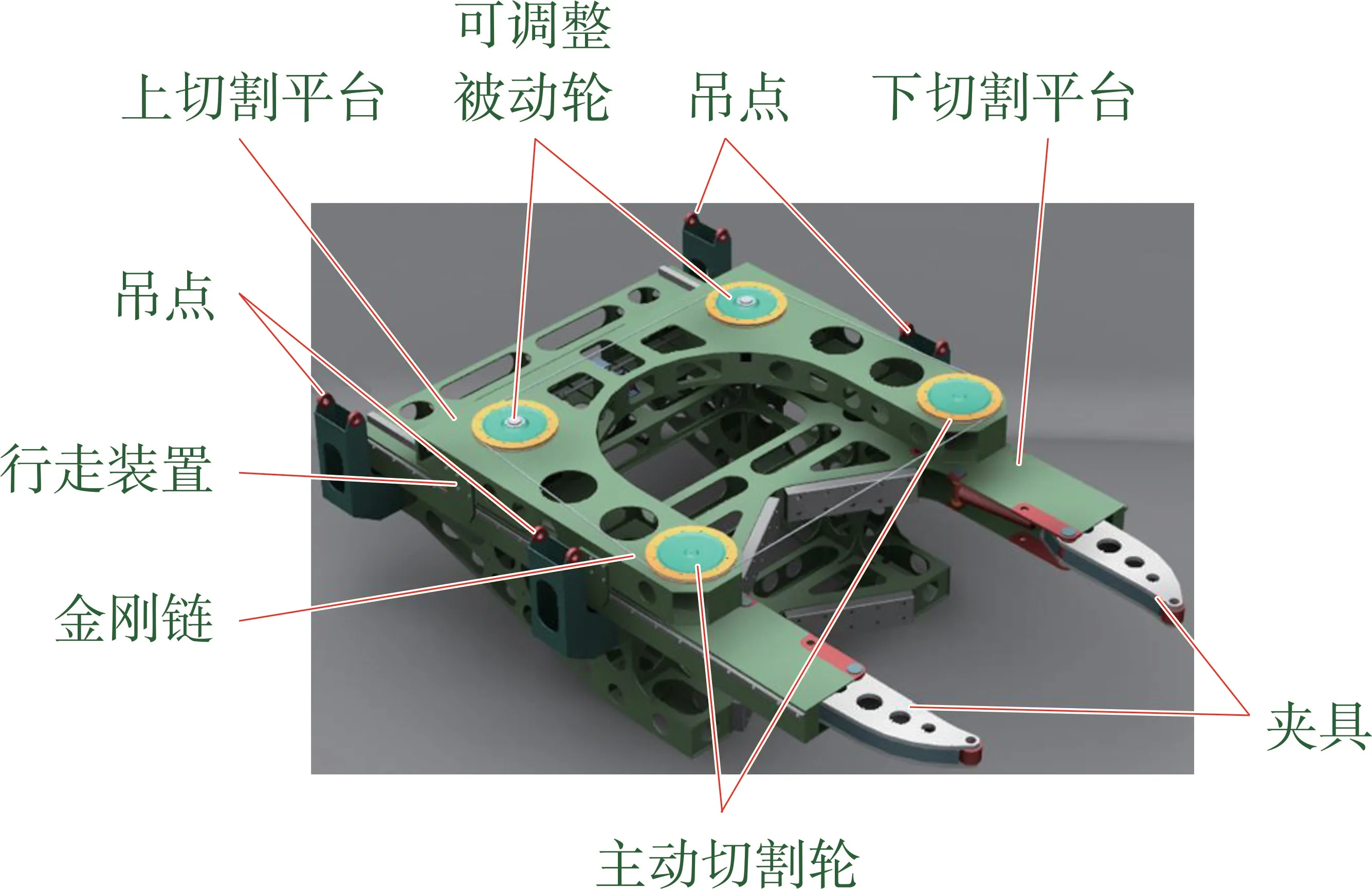
圖1 水下金剛石繩鋸機本體結構

(1) 將金剛石切割鏈整體看作是具有一定剛度的彈簧。

(2) 在切割過程中，金剛石切割鏈和滑輪不發(fā)生相對運動，受到的阻力與阻力矩均作用在滑輪上。

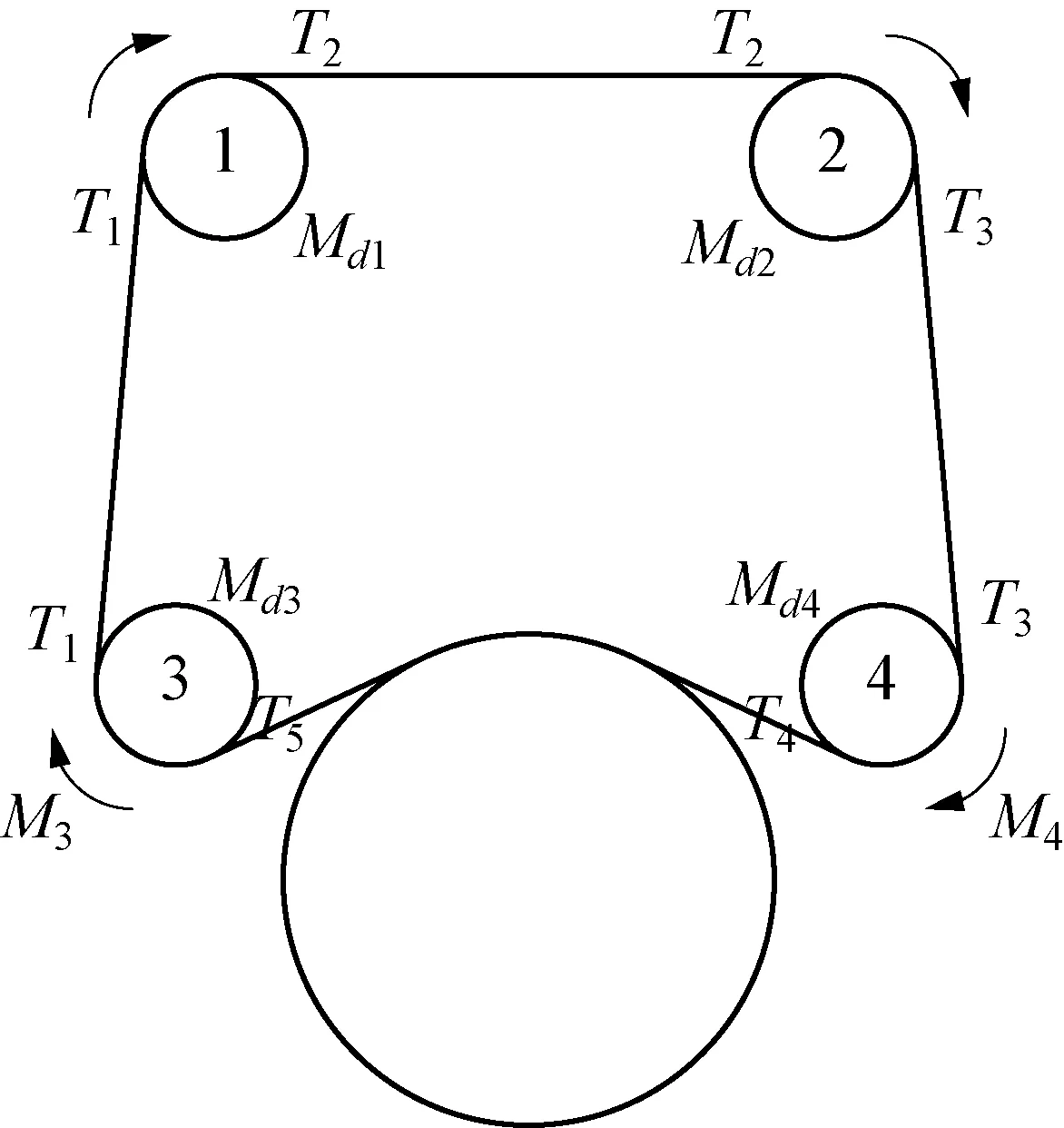
圖2 水下金剛石繩鋸切割系統(tǒng)動力學模型

在上述假設的基礎上，水下金剛石繩鋸切割系統(tǒng)的動力學方程為

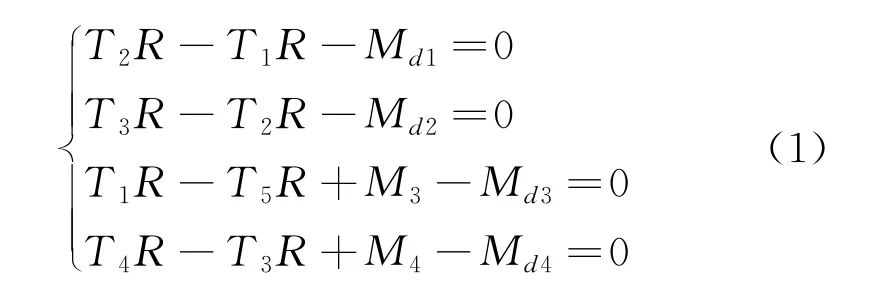
式中：R=262.5 mm，為切割滑輪的半徑；T1～T5分別表示各個滑輪兩側金剛石繩鏈的張緊力；M3與M4為主動輪3和輪4提供的驅動力矩，大小相等；Md1～Md4分別為4個滑輪在切割過程中受到的阻力矩，其中包括由于滑輪與鋸繩之間摩擦作用而產(chǎn)生的阻力矩。當繩鋸機在水下從事切割作業(yè)時，滑輪受到的海水黏滯力矩為阻力矩的主要組成部分，根據(jù)流體力學相關理論，海水黏滯力矩的大小[6-7]：

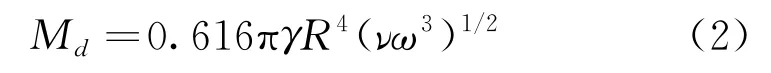
式中：γ=1 023 kg/m3，為海水的密度；ν=1.01×10-6m2/s，為海水的運動黏性系數(shù)；ω為滑輪轉動的角速度。

1.2 金剛石切割鏈張緊力分析

水下金剛石繩鋸通過驅動行進系統(tǒng)實現(xiàn)對工件的切割，當切割系統(tǒng)的進給速度與磨削工件的速度匹配時，切削壓力與鋸繩張緊力達到較為平衡的狀態(tài)，此時串珠與金剛石磨粒處于正常磨損狀態(tài)。增大行進系統(tǒng)前進油缸的壓力，使切割系統(tǒng)的進給速度超過磨削工件的速度，鋸繩會進一步張緊，進而增大磨削力，提升切削效率。但張緊力與磨削壓力過大時，一方面會加劇金剛石串珠與磨粒的磨損，另一方面，鋸繩也會有繃斷的風險。圖3所示為通過繩鋸切割試驗測得的鋸繩張緊力與其變形伸長撓度之間的關系，從圖中可以看出，在一定范圍內(nèi)，鋸繩的張緊力與其進給運動產(chǎn)生的撓度成近似線性關系，即

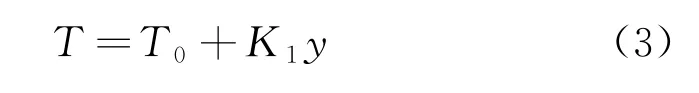
式中：T0為鋸繩的初始張緊力；y為鋸繩伸長的撓度；K1為鋸繩的剛度。圖3所示的關系也與上文所說的假設(1)相符。

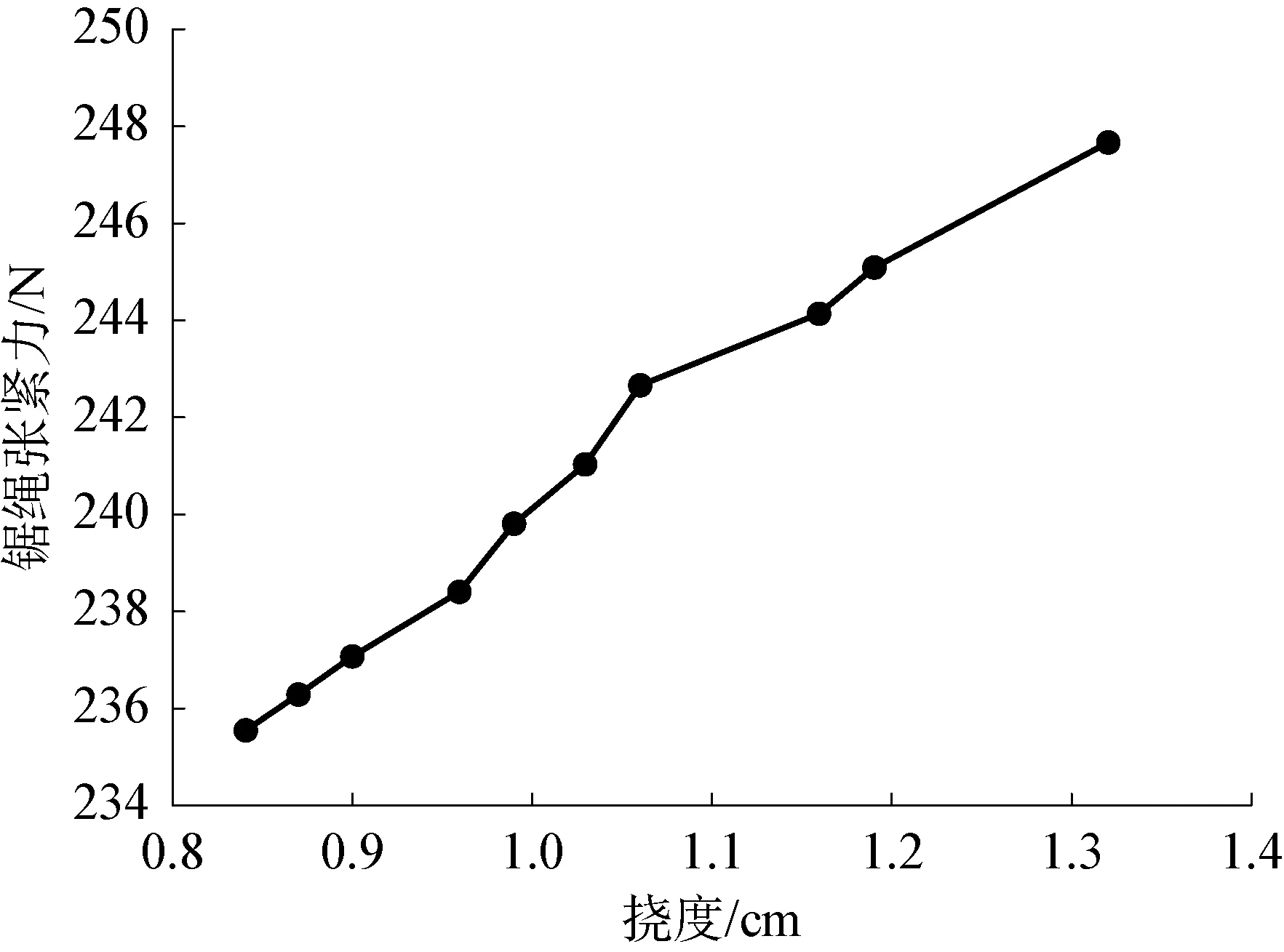
圖3 鋸繩張緊力隨撓度變化曲線

當量磨削厚度常被人們用來描述磨削過程[8]，根據(jù)Bus等的研究，當量磨削厚度與磨削工件所受的磨削力在一定范圍內(nèi)具有良好的線性關系[9]。對于金剛石繩鋸切割，在磨削過程中，工件由夾緊裝置夾持，保持固定，因而其當量磨削厚度可視作金剛石串珠繩的磨削厚度。設h為切削時金剛石串珠的磨削厚度，F(xiàn)t為主切削力，上述關系可以表示為

設串珠的寬度為b，則其沿切向的切削面積為

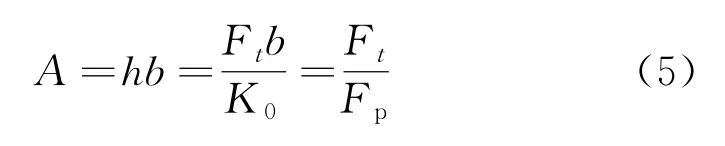
設鋸繩上相鄰兩串珠的間距為L，Vs為切割鏈轉動的線速度，則在單位時間內(nèi)，繩鋸切除工件的厚度，即繩鋸切削工件的速度為

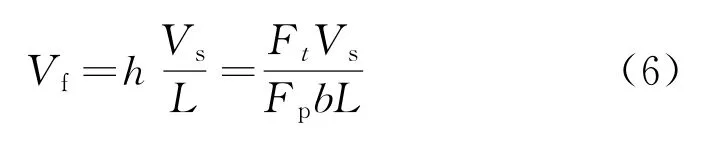
結合式(3)，若切割系統(tǒng)的進給速度為Vk，則在一小段時間dt內(nèi)，鋸繩張緊力的變化：

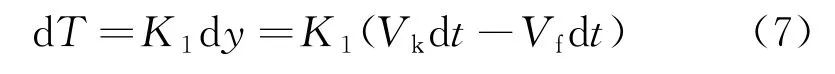
變化率為

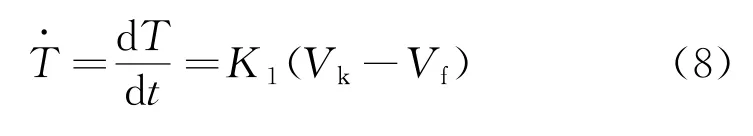
1.3 金剛石串珠切割過程力學分析

在金剛石繩鋸切割工件的過程中，單個串珠受力狀態(tài)如圖4所示，其兩端鋸繩拉力分別記為Ti與Ti+1，設單個串珠引起的鋸繩張緊力變化為dT，即Ti+1=Ti+dT。串珠受到工件的法向作用力Fn，用以磨削的切向作用力Ft。繩鋸在切割海底石油管道等工件時，以一定的弧度依附于工件表面，設單個串珠在工件上的包角為dα，則鋸繩張緊力與串珠運動方向夾角為在切割過程中，單個串珠尺寸相對于工件來說很小，則有

根據(jù)以上分析，串珠切向受力平衡方程為

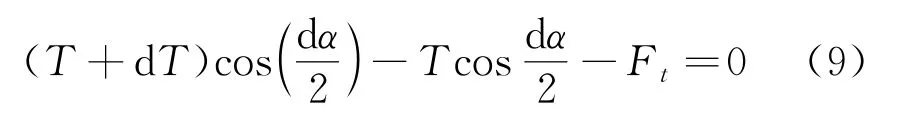
法向受力平衡方程為

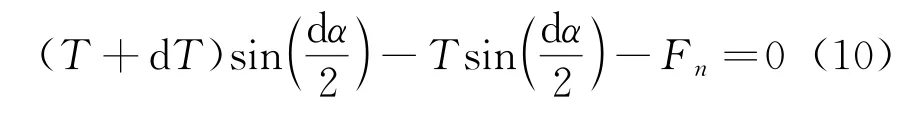
以上兩式整理后，可得

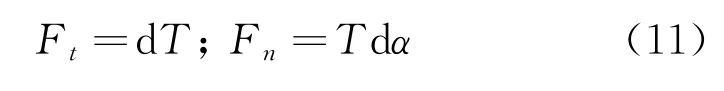
進一步可得

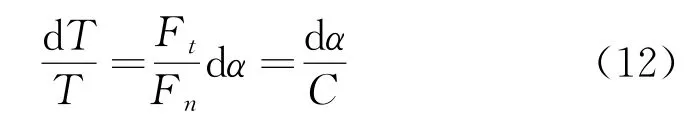
對式(7)左右兩邊進行積分，便可得到串珠兩側鋸繩張緊力之間的關系，即

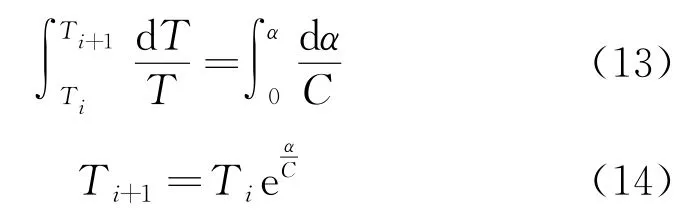
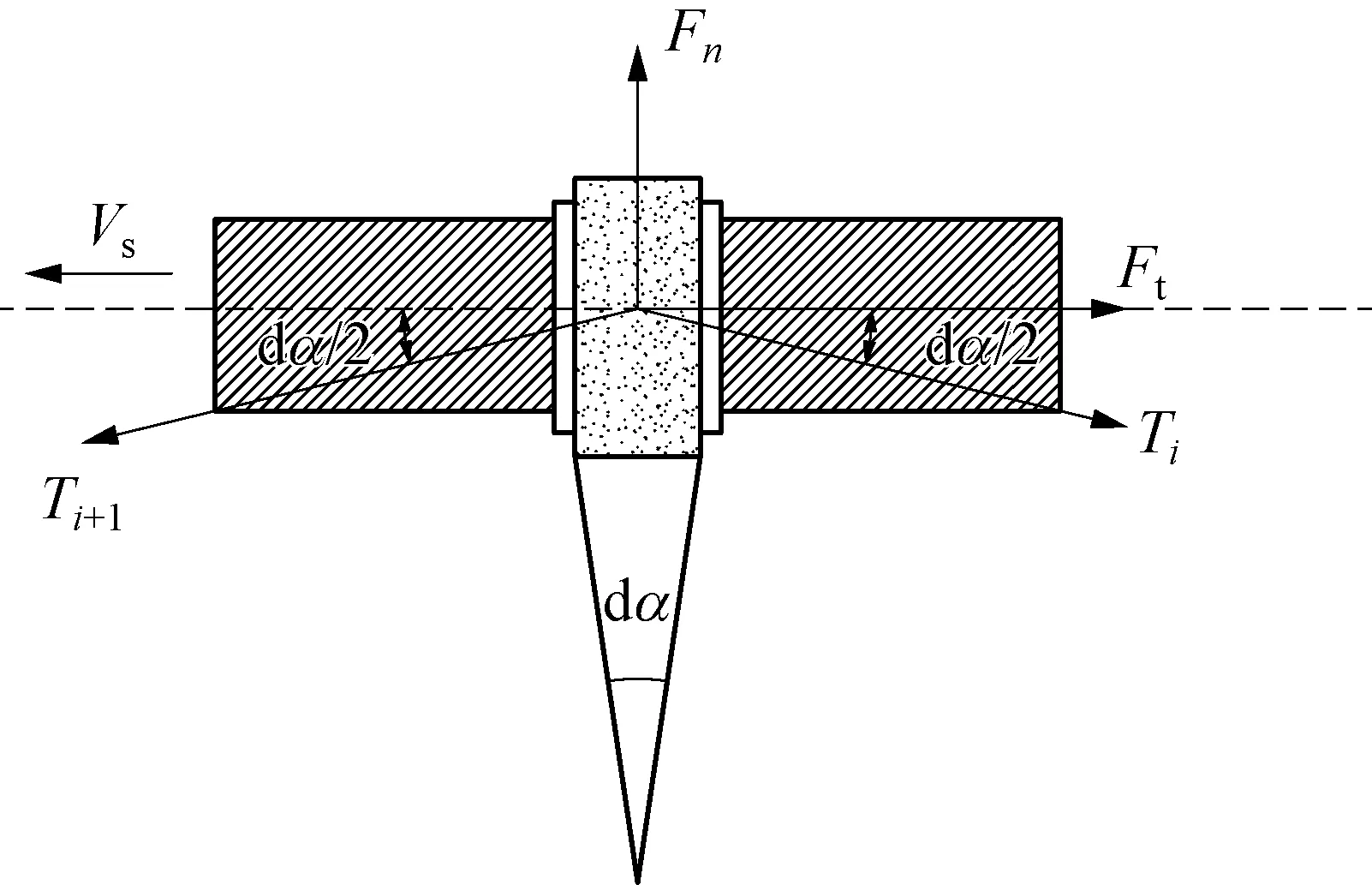
圖4 單個串珠切削過程受力分析

1.4 切割系統(tǒng)狀態(tài)空間

綜合上文給出的切割系統(tǒng)動力學方程式(1)以及式(8)、式(14)，金剛石繩鋸切割系統(tǒng)的狀態(tài)空間方程如下：

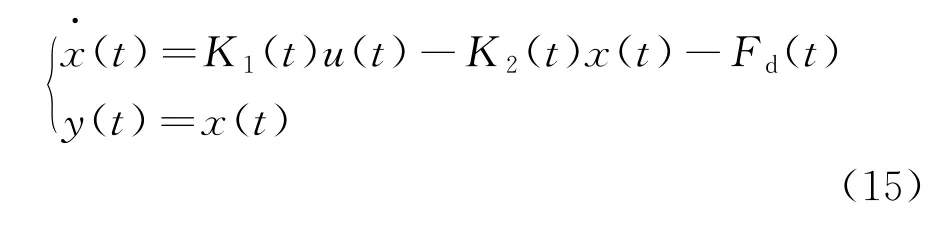
式中：x(t)=T1(t)，為切割系統(tǒng)從動輪處鋸繩張緊力；u(t)為切割系統(tǒng)的進給速度，即系統(tǒng)的輸入；y(t)為系統(tǒng)的輸出；K1(t)為鋸繩剛度系數(shù)；K2(t)是與繩鋸切割線速度、串珠自身形狀、工件材料特性等因素有關的參數(shù)；Fd(t)為系統(tǒng)的干擾，一方面來源于主動輪驅動力矩，海水黏滯力矩等，另一方面來源于信號干擾與測量誤差。從上面的狀態(tài)空間方程可以看出，切割系統(tǒng)是一個具有多參數(shù)的時變系統(tǒng)，隨著切割的進行，系統(tǒng)部分參數(shù)將會發(fā)生改變，造成系統(tǒng)的擾動。

2 模糊PID控制模型

在金剛石繩鋸切割過程中，切割鏈張緊力的大小與多種切削參數(shù)相關。本文考慮工程的實際情況，假設繩鋸機在切割過程中，主動切割輪轉速穩(wěn)定，金剛石切割鏈保持一定的線速度，此時切割系統(tǒng)的進給速度是影響切割鏈張緊力的主要因素。為避免切割鏈張緊力劇烈波動造成切割效率下降以及鋸繩斷裂，本文采用模糊PID控制策略對切割鏈張緊力進行控制。相比于傳統(tǒng)的PID控制策略，模糊PID控制根據(jù)傳感器反饋的張緊力的誤差與誤差變化率，通過模糊推理對切削狀態(tài)進行判斷與分類，再根據(jù)知識庫中的模糊規(guī)則選取合適的輸出，實時調整PID控制器的參數(shù)，使張緊力處于穩(wěn)定的狀態(tài)。

模糊PID控制模型如圖5所示，控制器以切割鏈預設張緊力T(t)與實際張緊力T'(t)的誤差值e(t)以及誤差值的變化率de(t)/dt作為輸入，經(jīng)過模糊推理環(huán)節(jié)后輸出PID控制器參數(shù)Kp、Ki、Kd的補償值ΔKp、ΔKi、ΔKd，從而調節(jié)PID控制器參數(shù)。對于PID控制器，其輸出為切割系統(tǒng)進給速度的控制量Vk(t)，控制方程為

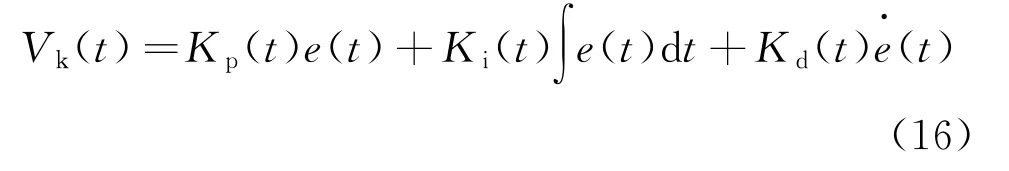
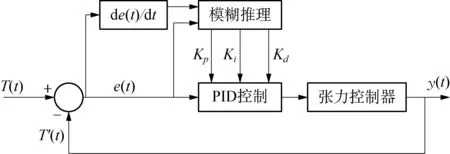
圖5 模糊PID控制模型

3 模糊PID控制仿真

3.1 恒張緊力仿真

為檢驗本文模糊PID控制方法對切割鏈張緊力的控制效果，采用仿真軟件進行相應仿真實驗分析，并將結果與傳統(tǒng)PID控制進行對比。模糊PID控制器的初始參數(shù)Kp、Ki、Kd與傳統(tǒng)PID控制器相同。控制系統(tǒng)的目標張緊力，根據(jù)相關試驗與金剛石切割鏈性能指標設為220 N，仿真總時間為200 s，采樣周期Ts=0.1 s。

切割系統(tǒng)狀態(tài)空間方程由式(15)給出，式中，鋸繩剛度系數(shù)K1=2 621 N/m，由試驗測得，在仿真過程中視為常數(shù)。系統(tǒng)狀態(tài)空間方程系數(shù)K2與線速度、串珠形狀、材料特性等因素有關，具有一定的時變性。為檢驗控制系統(tǒng)的魯棒性，引入系統(tǒng)參數(shù)的攝動，在t=100 s時將參數(shù)K2突然增大至原先的2倍。對于干擾項Fd，其來源于驅動力矩與阻力矩的部分，在仿真中保持不變；由于信號與測量誤差造成的系統(tǒng)干擾具有隨機性，因此在仿真過程中簡化為高斯白噪聲。

需要注意的是，在工程實踐中，切割系統(tǒng)的進給速度存在額定值與最小值，為了使仿真結果與實際情況更相符，在控制系統(tǒng)中加入篩選環(huán)節(jié)，使切割系統(tǒng)進給速度的控制量維持在其限定范圍內(nèi)。

模糊PID控制與傳統(tǒng)PID控制的仿真結果如圖6所示，從圖中可以看出，模糊PID控制的超調量與調整時間均小于傳統(tǒng)PID控制。當系統(tǒng)的參數(shù)發(fā)生突變時，模糊PID控制系統(tǒng)受到的影響較小，張緊力可以在很短的時間內(nèi)收斂到目標值，而傳統(tǒng)PID控制系統(tǒng)則會產(chǎn)生一定量的偏差，50～60 s后收斂到原設定值。以上結果表明，模糊PID控制具有較強的魯棒性。

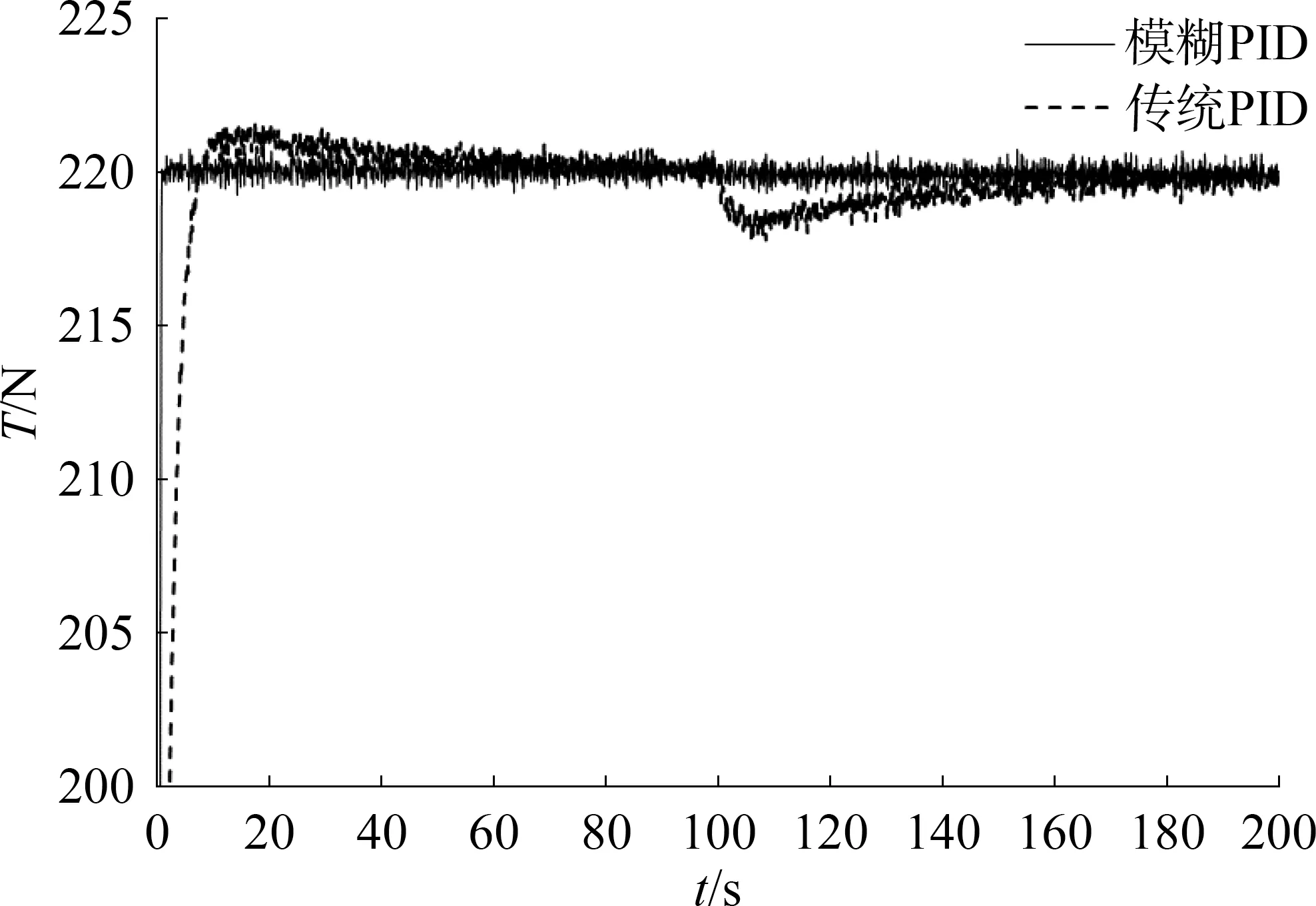
圖6 系統(tǒng)參數(shù)突變時的仿真結果

3.2 動態(tài)性能仿真

水下金剛石繩鋸在實際切削過程中，由于磨削力的限制，其磨削工件的速度相對較小，因而在工程實踐中，金剛石繩鋸磨削工件通常采用步進式的方案，即在短時間內(nèi)給行進系統(tǒng)一個較大的進給速度，使整個切割框架向前移動一小段距離。此時，鋸繩張緊力以及磨削力增大，繩鋸切削工件速度加快。隨著切削過程的進行，繩鋸的變形伸長逐漸恢復，張緊力不斷減小，直至達到平衡狀態(tài)。通過循環(huán)往復這一過程，實現(xiàn)對工件的切割。根據(jù)上文的描述，切割鏈張緊力在切削過程中表現(xiàn)為鋸齒狀的變化。為檢驗本文中模糊PID控制系統(tǒng)的動態(tài)性能，設置鋸齒力為系統(tǒng)輸入：

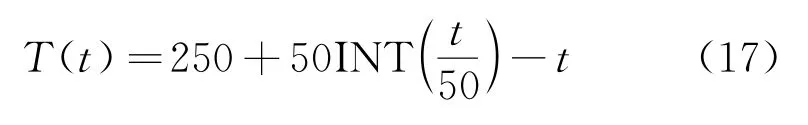
式中：INT()為取整函數(shù)，鋸齒力的峰值與谷值分別為250 N與200 N，周期為50 s。為進一步檢測控制系統(tǒng)的動態(tài)性能，相比于上述過程中張緊力的瞬時增長，考慮張緊力在每個步進周期內(nèi)緩慢增長的情形，設置正弦力作為系統(tǒng)輸入，同樣進行仿真試驗：

其中，正弦力的峰值與谷值分別為250 N與200 N，周期為100 s。

兩種目標張緊力及各自不同控制方式的仿真實驗結果如圖7與圖8所示。

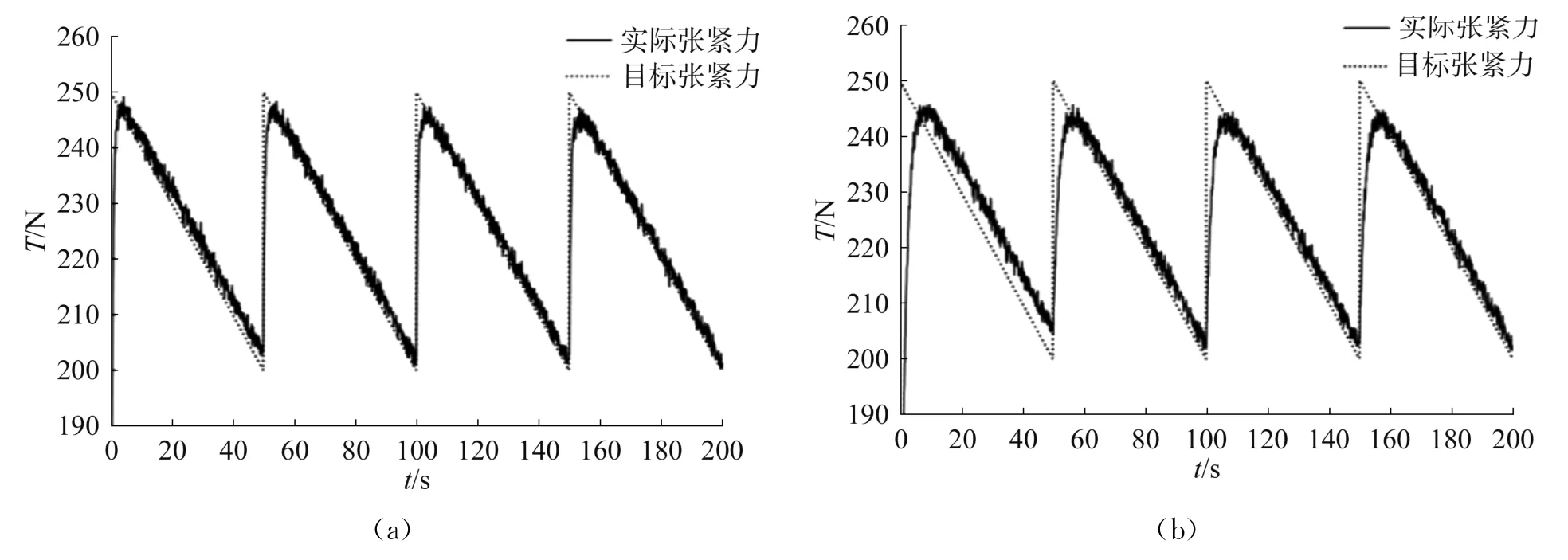
圖7 鋸齒力控制仿真結果

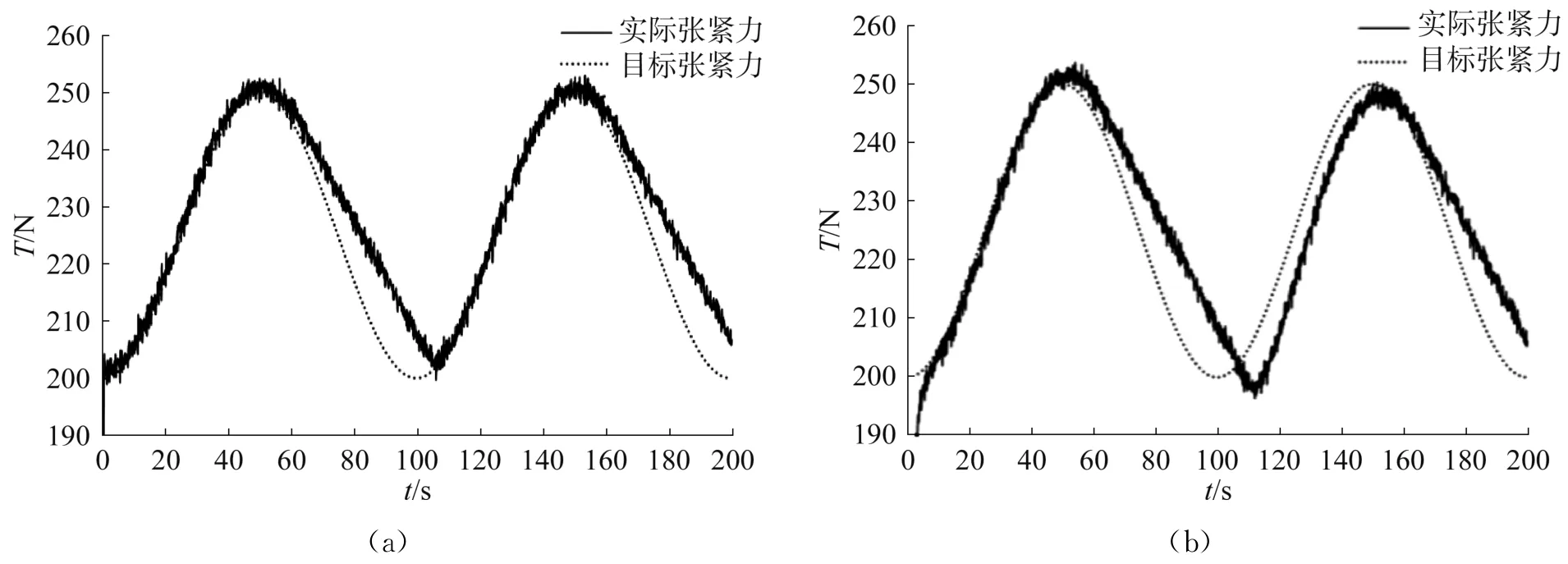
圖8 正弦力控制仿真結果

表1為模糊PID控制與傳統(tǒng)PID控制的性能指標的對比，結合表1與上文控制結果曲線，可以看出模糊PID控制相對于傳統(tǒng)PID控制具有響應速度快、平均誤差小以及波動較小的特點。對于鋸齒型目標張緊力，模糊PID的平均誤差為傳統(tǒng)PID的51%，標準差為傳統(tǒng)PID的66%；對于正弦目標張緊力，模糊PID控制的平均誤差為傳統(tǒng)PID的69%，標準差為傳統(tǒng)PID的90%。以上結果表明，本文采用的模糊PID控制系統(tǒng)對于動態(tài)控制目標具有較好的控制效果和性能，可以有效提高控制精度。

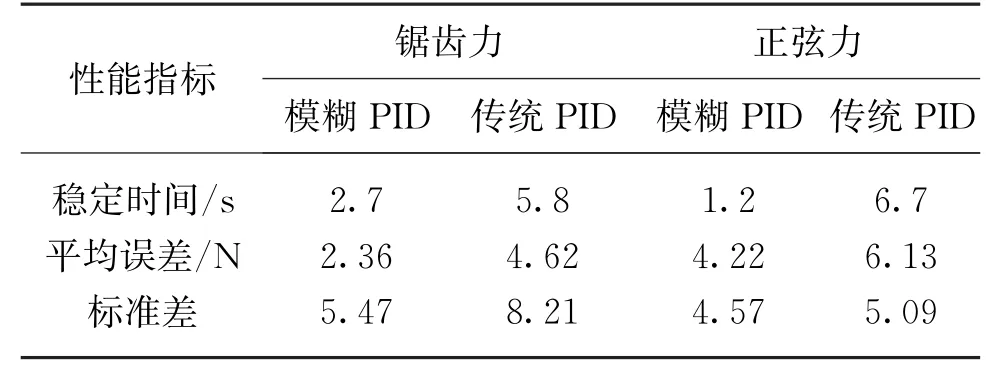
表1 兩種方式控制性能對比

4 結 語

本文首先從整體上建立了金剛石繩鋸切割系統(tǒng)的動力學模型，之后從總體到局部，對切削過程中鋸繩自身以及單個串珠進行了力學分析，將以上各個力學方程串聯(lián)，構建了以切割系統(tǒng)進給速度為輸入，切割鏈張緊力為輸出的切割系統(tǒng)狀態(tài)空間方程。

在切割系統(tǒng)狀態(tài)空間方程的基礎上，提出了一種基于模糊PID的切割鏈張緊力控制策略。進行恒張力控制仿真實驗，在仿真中引入系統(tǒng)參數(shù)的攝動。結果表明，模糊PID控制策略相較于傳統(tǒng)PID控制具有更強的魯棒性。同時進行動態(tài)張緊力控制仿真實驗，仿真結果顯示模糊PID控制的動態(tài)性能優(yōu)于傳統(tǒng)PID控制，能夠有效減小切削過程中切割鏈張緊力的波動，提高控制精度。

水下金剛石繩鋸機張緊力受多種切削參數(shù)影響，本文以進給速度為控制量，提出的模糊PID控制策略對于工程實踐中切割鏈張緊力的控制以及切削效率的提升具有參考意義。