新型外轉子升船機的研究與探索
李昕濤,韓增強
(1.太原科技大學 重型機械教育部工程研究中心,山西 太原 030024 ;2.太原科技大學 電子信息工程工程學院,山西 太原 030024)
0 前言
在內河通航中,傳統的多級船閘[1]通航,存在著下泄內河大壩的蓄水水量,直接造成大壩發電量的減少,綜合效益的下降;而垂直升船機具有在不影響大壩蓄水量的同時,可以有效實現內河船舶的通航[2,3]。目前,國內外在航運領域,將船舶提升一定高度所采用的裝置有多種,如電動卷揚機提升、齒輪齒條傳動提升、水利驅動提升等[4,5];現有垂直升船機結構復雜、運營成本高,由于提升承船廂載荷大,往往需要多臺大型電機同步驅動,加之確保船舶穩定提升,造成了控制難度高,往往帶來通航能力取決于垂直升船機的安全運行能力[6,7]。據此,本文提出了外轉子電機拖動的升船機[8]。
1 外轉子升船機的結構
新型外轉子升船機結構如圖1所示,在壩體之間的水面上放置有承船廂,承船廂通過皮帶,并經過第一導向輪與外轉子電機的兩側轉筒連接。壩體的外側分別設有配重,配重通過皮帶,并經過第二導向輪與外轉子電機兩側轉筒連接;外轉子電機及其提升機構結構相同,對稱布置安裝在壩體上。
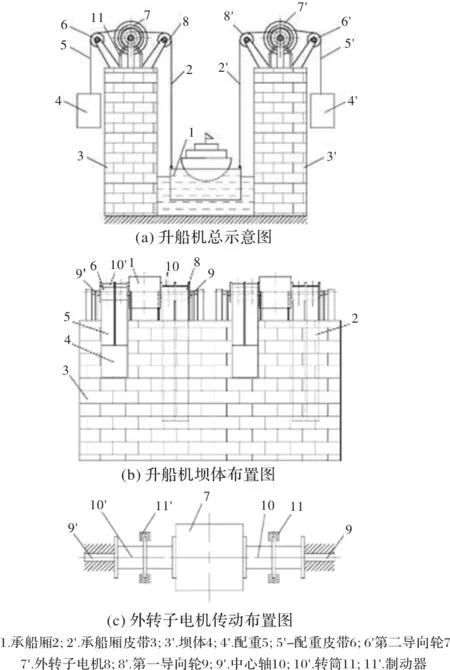
圖1 升船機結構示意圖
升船機單側外轉子電機傳動布置,如圖1c所示,外轉子電機的中心軸通過支架固定安裝在壩體上,在其皮帶轉筒通過螺栓與皮帶連接,在皮帶轉筒的中間位置安裝有前后制動器。
此時,配重抵償升船廂自重,外轉子永磁同步電機僅提供運行的驅動力,減少運營成本。在軸承載荷平衡的情況下,外轉子電動機驅動僅需克服軸承的摩擦力,實現升船機勻速起降運行。
2 垂直升船機力學分析
2.1 外轉子電機驅動的力學分析
如圖1所示,設承船廂的驅動力為F驅動,根據靜力學力學定律(以向上為力的正方向)可知:
F驅動+G配重-G承船廂=M承船廂a承船廂
在確保水位不變的條件下,承船廂內的船舶數量與大小,都不影響升船水廂的重量G承船廂;因此,當外轉子電機驅動的垂直升船機結構確保了承船廂與配重等重時,其外轉子電機的驅動力F驅動僅提供了升船機升降時所需承船廂升降加速度a承船廂的力,即當G配重=G承船廂時,F驅動=M承船廂a承船廂。此時,設承船廂對通航船舶的浮力F船浮力,根據阿基米德原理和牛頓力學定律知,承船廂中船舶的受力F船舶為
化簡可得
可知,船舶的提升(下降)加速度取決于排開水體積V船排的變化,設排開水體積V船排的變化為ΔV船排,則有
V船排+ΔV船排=a承船廂b承船廂(h液面+Δh液面)
式中,a承船廂為承船廂的長度;b承船廂為承船廂的寬度。
由此可知,船舶排開水體積V船排的變化,提供了船舶的加速度a船舶,由于承船廂水量一定,船舶排開水體積V船排變化ΔV船排,引起承船廂中液面高度h液面發生相應的變化Δh液面,承船廂水位的升高或下降提供了船舶上升或下降的動力。
設升船機承船廂中運送n艘船只,暫不考慮船只間的耦合振動對承船廂液面的影響下,則n艘船只對承船廂液面變化的影響為
將其列寫微分方程為

每艘船的排開水的體積和其吃水線有關,當升船機向上提升時,每艘船相對于水面向下運動深度是不同的,船舶側立面對水的壓力也不一樣,因此,產生水面的波動,帶來承船廂的擺動[9-11]。
此時,若承船廂中通航船舶型號一致時,根據水彈性動態響應,易引發水體的共振,帶來控制難度增加。外轉子電動機驅動可以實現勻速運行,僅在其加、減速過程出現共振問題,通過智能算法的平滑性控制和制動器的投入,可以有效地減少承船廂水體的晃動。
2.2 承船廂運行偏載受力的分析
由于承船廂上下運行時,由于多吊點運行,傳統的起升機構會帶來側傾,以三峽升船機為例,三峽承船廂長×寬×高(100m×20m×18m);若兩側高差相差1 cm,計算其兩側重量差為
G偏載=ρ液V偏載g=20 t
顯而易見,承船廂兩側高差1 cm,偏載20 t。當承船廂向上起升時,承船廂中各船只對承船廂水位影響不同,會帶來動態偏載問題。根據垂直升船機外轉子電機驅動與承船廂運行偏載受力的理論分析,必須提供一種特定的智能控制算法,才能主動防御外轉子電動機拖動的升船機的載荷波動、偏載問題。通過外轉子永磁電機的固定時間超螺旋智能控制方法,來解決超大慣性升船機的載荷沖擊問題。
3 固定時間超螺旋的智能控制算法的研究
固定時間超螺旋的智能控制方法可以在不依賴于系統初值的情況下,使系統以固定的時間收斂,改善了其收斂可靠性, 并提高了其響應時間。也就是說,自由狀態下,升船機配重不能恒等于承船廂重量,帶來承船廂水位的晃動,引起外轉子電機負載不平衡的狀態;不論初始情況下電機載荷是否一致,均布在壩體上的外轉子電動機,都能在固定時間內準確到達承船廂預期的固定位置。每臺電機都按照這一要求智能運行,各自采用這樣的算法到達控制目標位置。在上百臺外轉子電動機實際運行中,一旦出現電機隨機損壞后,剩余多臺電機載荷突然變化,升船機依然可以正常運行。即升船機實現智能故障容錯,這對于內河通航意義重大。
3.1 外轉子永磁電動機數學模型的建立
升船機采用表貼式外轉子永磁同步電動機,對于表貼式外轉子永磁同步電動機,考慮到id對電機調速影響很小,可令id=0,建立d-q坐標系下的外轉子永磁同步電動機數學模型[12,13]。
式中,ud、id、Ld、Lq、uq是坐標系變換后定子電壓、電流和電感在直軸(d軸)和交軸(q軸)上的分量值,且滿足Ld=Lq=Ls;R為定子電阻;pn為電機磁極對數;ψf為永磁體與定子交鏈的磁鏈;Te和TL則分別為電磁轉矩、負載轉矩;J為轉動慣量;ω為轉子機械角速度;B為摩擦系數。
外轉子永磁同步電動機的調速系統的控制器以級聯的形式分別構成速度外環和電流內環。其結構圖如圖 2 所示。
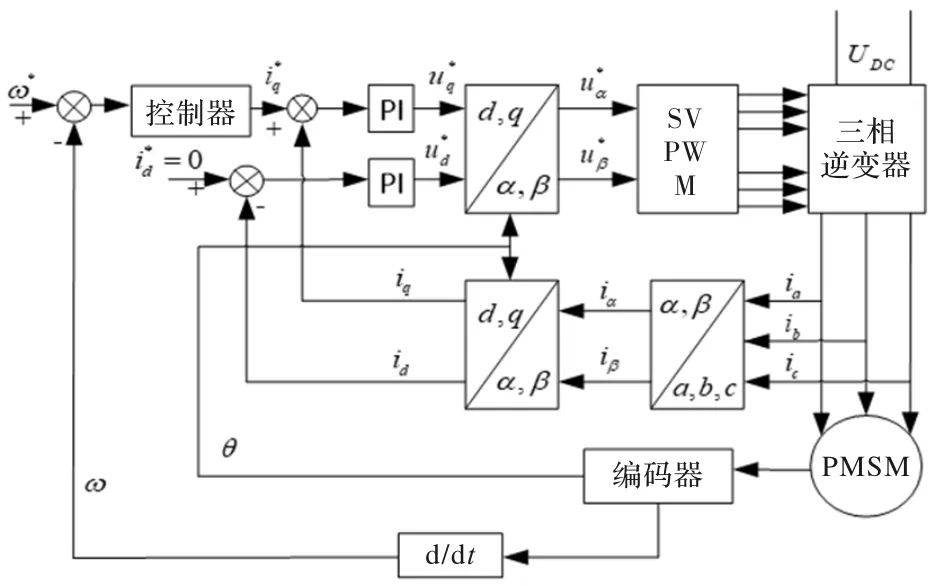
圖2 外轉子永磁電動機控制系統框圖
3.2 外轉子永磁電動機數學模型的建立
3.2.1 固定時間收斂控制律
考慮微分方程的系統:
(1)
式中,x=[x1,x2,…,xN]T∈RN,F(x):D∈RN在原點的開區間D∈RN上是連續的,且F(0)=0。
若任意給定初始時間t0和初始狀態x0∈D,都存在時刻T(x0),使系統(1)的每一個解x(t)滿足關系
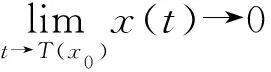
(2)
則系統(1)的平衡點x=0是有限時間穩定的,如果原點是在N=RN有限時間穩定,則其是“全局有限時間穩定”平衡。此外,原點的有限時間穩定性意味著原點的漸近穩定性。學者 Zuo Z 提出了固定時間穩定性的概念,無論初始條件如何,都能提供收斂時間的一致有界性[14]。
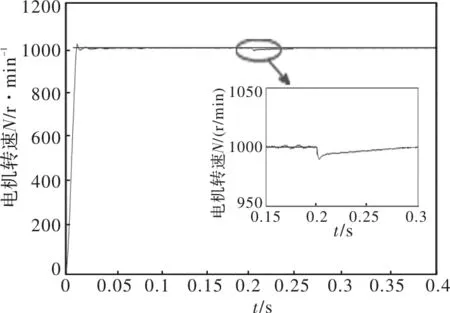
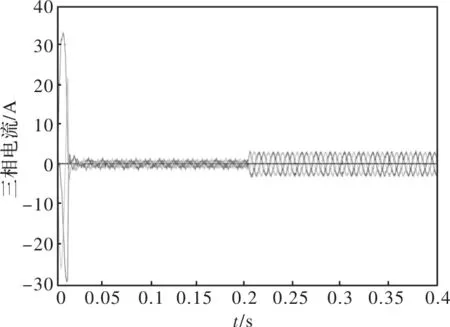
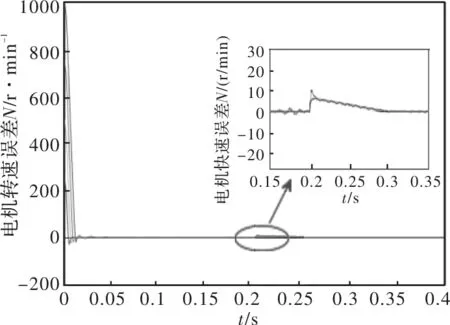
定義1:原點被認為式(1)的“固定時間穩定”平衡點,如果全局有限時間穩定的并且建立時間函數T(x0)是有界的,即,存在Tmax>0,且 ?x0∈RN,都有T(x0) 引理1:考慮一個標量系統 (3) 其中α>0,β>0,并且m、n、p、q是滿足m>n且p (4) 由式(4)可知,系統的收斂時間僅依賴與系統的固有參數m、n、p、q、α和β,與系統的初始狀態無關,因此可以以設定的方式保證收斂時間。 3.2.2 固定時間超螺旋收斂控制律 定義:本文所提出的式(1)被稱為是在原點處收斂的固定時間。若存在一個時間T,對所有t≥T從任何初始條件x0開始,都有系統的狀態x(t)=0成立。 Panathula,等學者提出并研究一個連續的控制率[15]: (5) 式中,λ1,λ2,a>0 且p>1。 從而得出系統的超螺旋控制率的表達為 (6) 考慮動態系統存在的擾動ξ(t),以常數L為邊界,則狀態變量x(t)和y(t)均在固定時間內均勻的收斂于原點。 (7) 由式(7)可知,公式右邊代表的是超螺旋系統(式6)的收斂固定時間的上限估計,此值獨立于未知的初始值,并不受初始狀態x(0)的影響。這意味著對于任何初始條件x(0),公式(6)所表示的超螺旋系統的兩個狀態變量x(t)、y(t)在有限時間Tf不大于式(4)中的上限估計值時,均能可靠收斂到原點。 3.2.3 速度控制器設計 對固定時間以及超螺旋控制率的數學模型分析,設計外轉子永磁同步電動機的控制器。 定義外轉子永磁同步電動機的狀態變量: x1=ωref-ω (8) 式中,x1為控制系統的角速度誤差;ωref為給定的機械角速度;ω為實際角速度。 考慮到摩擦系數B很小,忽略摩擦系數,由公式(1)可得, (9) 定義iq為u,則式(9)變為 (10) 基于固定時間理論表達式(3)和超螺旋表達式(6),故而,可將控制器設計為 (11) 將式(11)代入式(10)中可將其變形為 (12) 式(12)為所設計的超螺旋固定時間控制方程。由固定時間定理的公式(4)可知,系統的收斂時間T與系統的初始變量參數無關。 為驗證設計控制器(12)的穩定性,定義 Lyapunov 函數為 (13) 同時,由建立的時間 可知,系統的收斂時間不大于(4)中的上限估計值,故均會可靠收斂到原點。 在Matlab/Simulink中搭建外轉子永磁同步電機調速系統仿真模型[16-18]。用以驗證該控制算法的可靠性,仿真中所用電機的參數設置為定子電阻R=2.875 Ω, 定子電感Ls=8.5 H,轉動慣量J= 0.003 kg·m2,永磁體磁鏈f=0.175 Wb。仿真結果如圖 3~7 所示。 圖3 轉速的仿真結果 圖4 三相電流的仿真結果 圖5 電磁轉矩的仿真結果 圖3 ~圖5分別為電機轉速為1 000 r/min 時的轉速、三相電流以及電磁轉矩的仿真結果圖。可以看出,轉速的動態響應快,超調量小,同時在 0.2 s 時突加負載TL=2 N·m后,快速穩定性。 設置電動機轉速的初始誤差分別為250 r/min、500 r/min、750 r/min、1 000 r/min,圖6在0.2 s時突加負載后,四種不同初始誤差的響應曲線均在約0.1 s時間內收斂到零,且抖振較小,較好的提高了系統的抗干擾能力。由圖7可知,系統在不同的初始轉速誤差的條件下,其轉速誤差減小到零的時間基本一致,即其收斂時間均約為0.02 s,與初始誤差無關。 圖6 0.2 s突加負載時的仿真結果 圖7 四種不同轉速誤差下的收斂時間仿真結果 外轉子永磁電動機在升船機載荷不均的狀態下,可實現速度快速同步;承船廂與每個外轉子電機速度一致,即動態平衡運行[19-20]。 本文對外轉子升船機進行了力學理論分析,并通過理論分析得出結論: (1)外轉子升船機采用配重抵償升船廂自重,電機僅提供承船廂運行的動力,大大降低了垂直升船機運行成本。 (2)自由狀態下,配重與承船廂重量偏差來源于——承船廂升降過程中水位的晃動,故外轉子電機載荷不均衡; (3)通過對固定時間超螺旋智能算法應用于外轉子永磁電機控制的研究,其仿真結果表明智能算法有效實現動態平衡運行;為新型外轉子升船機的研制提供了理論依據。
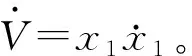
3.2 仿真結果分析


4 結論

