不同轉速下低速重載齒輪動態磨損特性研究

盧 玲

(吉林電子信息職業技術學院，吉林 吉林 132021)

0 前言

齒輪作為重型機械領域中應用最為廣泛的傳動部件之一，其使用壽命直接關系到機械的整體壽命。磨損作為不可避免的一種故障形式，準確預測齒輪磨損過程對齒輪壽命分析具有重要的研究意義。在低速重載條件下，齒輪表面油膜難以形成，齒輪的主要磨損形式為粘著磨損，導致齒輪表面產生嚴重磨損[1]。無法準確估計齒輪表面磨損發展過程將導致齒輪有過度的冗余設計，進而導致機械重量增大，成本增加，運行與維護難度大。Flodin等人針對齒輪粘著模型進行了研究，將Archard磨損模型引入到齒輪磨損計算中，提出了齒輪磨損的計算模型，為齒輪磨損問題奠定了基礎[2-4]。潘東等人充分考慮了齒輪負載及轉速對齒輪副齒面磨損的綜合影響，建立了齒輪磨損壽命預測模型，但僅僅考慮了單一齒輪在恒定工況下的齒輪磨損壽命預測[5]。馮松等人對齒輪齒面磨損對齒輪剛度的影響進行了分析，結果發現磨損對齒輪剛度的影響可以忽略，該研究對齒輪磨損后剛度計算的簡化提供了依據[6]。周長江等人則針對圓柱斜齒輪提出了在準靜態和動態載荷下的粘著磨損計算，并計算出磨損后的動力學特性[7]。本文結合Archrad磨損模型，充分考慮齒輪的內部和外部激勵，得到齒面的動態載荷分布，從而計算齒輪齒面磨損分布。

1 磨損模型

粘著磨損計算首先是由Archard提出，計算粘著磨損公式為[8]

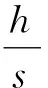
(1)

式中，h為磨損厚度；s為相對滑動距離；k是磨損系數；p為觸壓力；由式(1)可以得

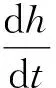
(2)

式中，v是滑動速度；在齒輪磨損計算中需要進行離散化分析，可以得到離散化齒輪磨損計算公式為

hi,j=hi,j-1+kpi,j-1vjΔt

(3)

式中，hi為i微元內的齒輪磨損深度，i為嚙合點所在單元，j為p點的磨損次數；p為嚙合點所受壓強；vp為嚙合點滑動速度；Δt為時間步長。齒面磨損離散化模型具體如圖1所示。

圖1 齒面離散化

圖中θ1和θ2為齒輪旋轉角度；v1和v2為齒輪齒面線速度，vp=v1-v2。

2 齒輪動力學模型

本文以直齒輪為研究對象，建立2個自由度的動力學模型，分別為內外齒輪的角位移θ1和θ2，具體如圖2所示。其中，Rb1、Rb2分別為外、內齒輪基圓半徑；T1、T2分別為輸入、輸出力矩；I1、I2分別為外、內齒輪轉動慣量；m1、m2分別為外、內齒輪的質量；Ke(t)為齒輪時變嚙合剛度；c(t)為時變嚙合阻尼；e(t)為齒輪齒廓誤差；f(δ)為齒輪應變函數。

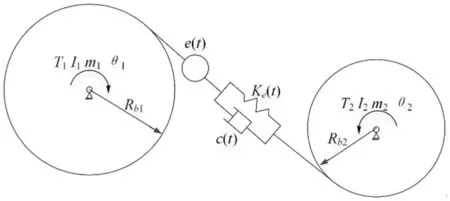
圖2 內嚙合直齒輪動態嚙合模型

為求解動態嚙合力，將角位移θ1、θ2轉化為嚙合方向的線位移y1、y2。假定Fd表示外部載荷力，則Fd滿足Fd=T1/Rb1=T2/Rb2可得[9]

(4)

式中，S1i=ρ1i/Rb1，S2i=ρ2i/Rb2分為外、內齒輪嚙合點處曲率半徑與其基圓半徑之比。

對于任意嚙合齒對i，其動態嚙合力可以表示為

Fi=Kei(xr-e)

(5)

其中，當xr-e≤0時齒輪嚙合點處的嚙合力為0，當xr-e>0時Fi>0。

將式(6)代入式(5)整理后可得

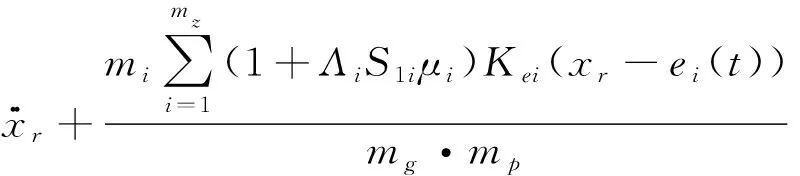
(6)

將粘性阻尼考慮進去整理后可得

(7)

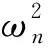
3 齒輪嚙合剛度

根據最小勢能原理可以準確求解出齒輪嚙合剛度。通過計算在齒輪接觸過程中的各應變勢能，累加后得到總應變勢能，從而計算總的接觸剛度。計算的直齒輪輪齒的彈性勢能U可以表示為彎曲勢能Ux、擠壓勢能Un和剪切勢能Us[11]：

U=Ux+Un+Us

(8)

所有的勢能可以通過彈性理論公式進行計算：

(9)

式中，F為兩齒間法向接觸力；ξP為P點壓力角；B為齒輪軸向寬度；E為彈性模量；G為剪切彈性模量；y為齒輪截面旋轉中心坐標；e(y)為y的函數，表示y對應的齒輪截面齒厚；yb和yP分別為根截面和載荷截面對應的值；Cs為當量修正系數，這里取值為1.5；具體參數如圖3所示。

圖3 齒輪幾何參數

可以將U轉化為關于嚙合壓力角ξP的函數，計算公式為

式中，ξP與嚙合參數有關，γb為齒輪根部角厚度。

在齒嚙合過程中會出現多對齒同時參與嚙合的情況，得到多齒彈性勢能Uz。

(10)

式中，在當齒輪嚙合點的嚙合參數為ξP時，其相鄰齒面嚙合點參數分別為ξP+1和ξP-1。為得到不同輪齒的齒面載荷，定義Us的逆函數Vs滿足以下條件

(11)

4 齒面磨損計算

主動輪齒輪模數為5.5，壓力角為0.35 r/min，輸入功率為50 kW，其他參數如表1所示。

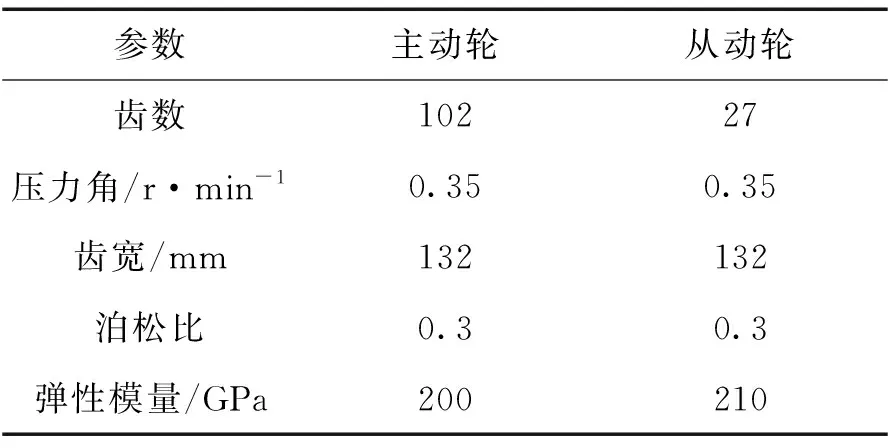
表1 齒輪參數

將齒輪從進入嚙合到退出嚙合等間距分割成100個時間步長，并假設每個時間微元內認為齒輪齒面幾何參數不變。為求解齒輪運行過程中的齒面動態載荷隨時間變化的函數，需要求解出齒輪齒面的穩態載荷分布，并結合龍格庫塔法進行迭代求解。計算流程圖如圖4所示。

圖4 齒輪表面磨損流程圖

根據最小勢能法可以計算得到齒輪穩態狀態下的齒面嚙合力，并作為計算迭代的初值進行計算。同時為研究不同轉速下對齒輪磨損的影響，分別計算在主動輪轉速分別為10 r/min、40 r/min、70 r/min時的嚙合力,如圖4所示。

圖5 齒輪齒面滑動速度和齒面嚙合力

圖5中Tz為輪齒嚙合周期。可以看出齒輪在單-雙齒嚙合過程中兩次明顯突變。而在動態條件下的低速齒輪齒面嚙合力如圖6所示。

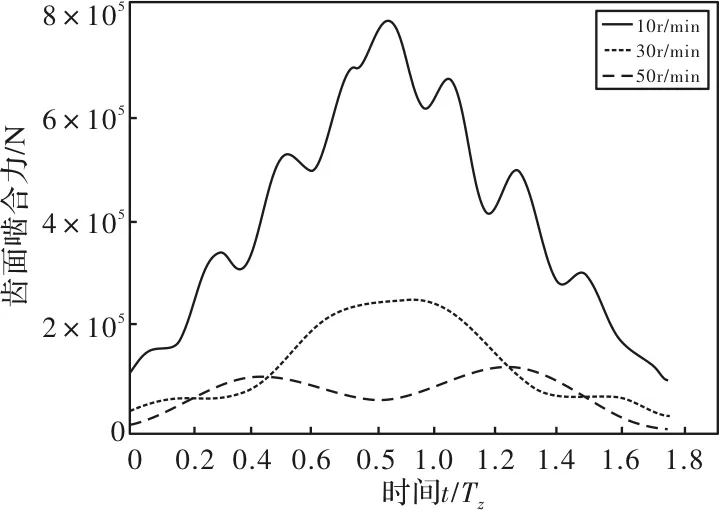
圖6 齒輪齒面滑動速度和齒面嚙合力

從圖6中可以看出，在功率不變時，齒輪轉速增加齒輪齒面嚙合力從10 r/min時的多峰分布逐漸轉變為30 r/min和0 r/min時的雙峰分布。此時齒輪齒面嚙合力呈明顯的動態特征。

分別計算轉速為10 r/min、30 r/min和50 r/min時，主動輪和從動輪經過10 000、20 000、…、100 000次嚙合厚度的齒輪表面磨損分布，如圖7～圖12所示。

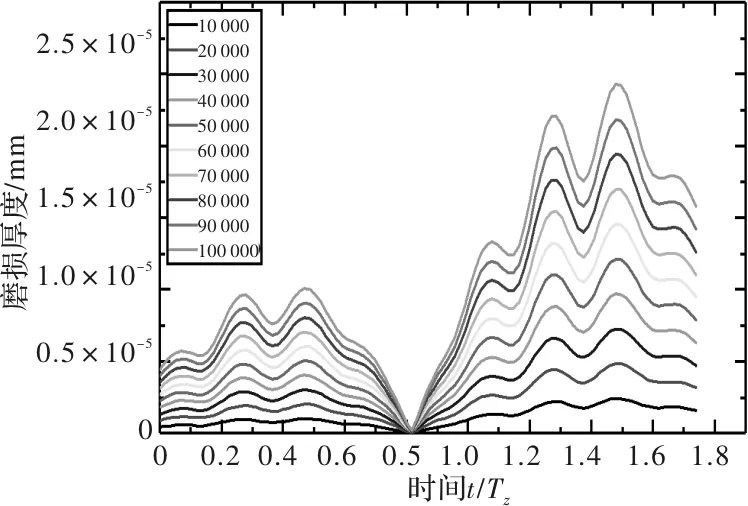
圖7 10 r/min時主動輪齒面磨損分布

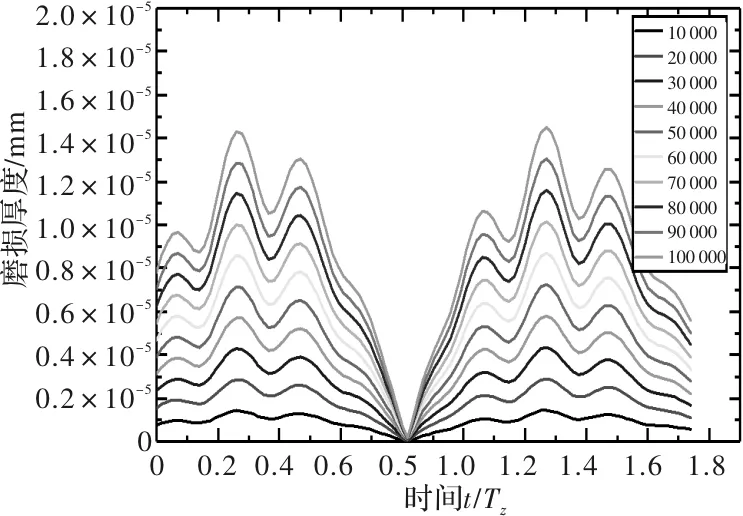
圖8 10 r/min時從動輪齒面磨損分布

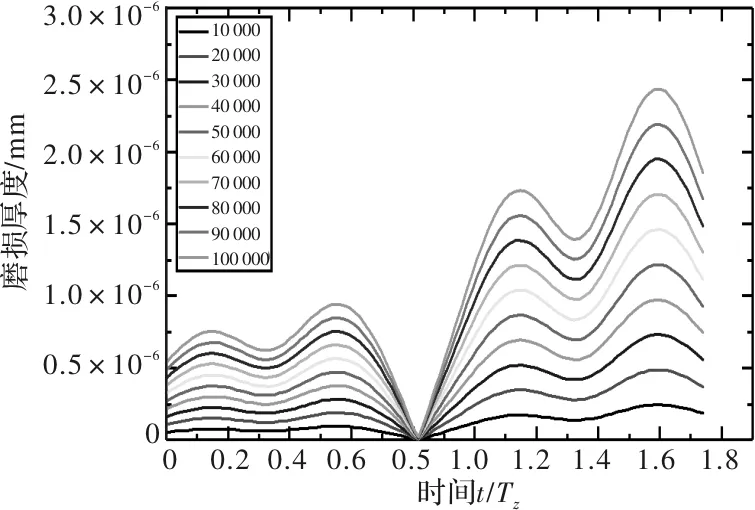
圖9 30 r/min時從動輪齒面磨損分布

圖10 30 r/min時從動輪齒面磨損分布

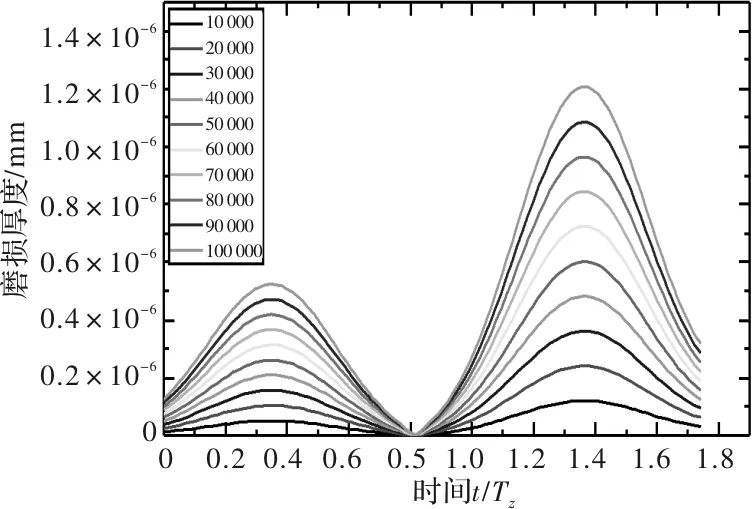
圖11 10 r/min時從動輪齒面磨損分布

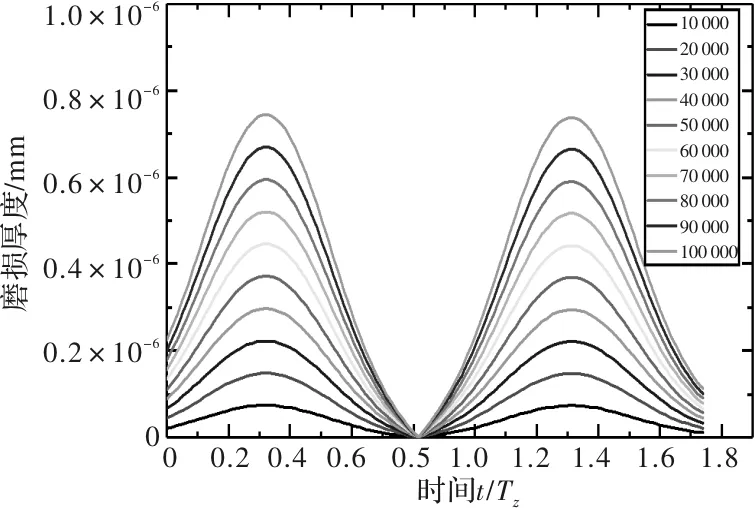
圖12 10 r/min時從動輪齒面磨損分布

從圖7～圖12中可以看出，主動輪在進入嚙合段時的磨損較退出嚙合段有明顯減少，同時從動輪在進入和退出嚙合段的磨損較為均衡。且主動輪最大磨損較從動輪增加約67%。同時在功率不變時，隨著轉速增加，齒輪表面磨損逐漸平緩，齒輪齒面磨損量減少。

王曉筍等人則基于齒輪準靜態條件計算齒輪齒面磨損分布，具體如圖13～圖18所示[12]。

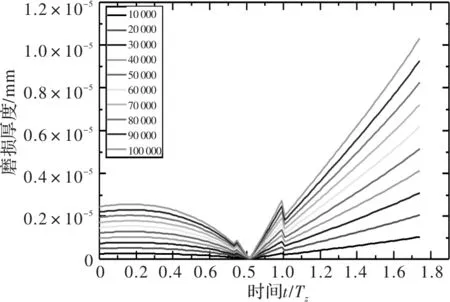
圖13 準靜態條件下10 r/min時主動輪磨損厚度

圖14 準靜態條件下10 r/min時從動輪磨損厚度

圖15 準靜態條件下30 r/min時主動輪磨損厚度

圖16 準靜態條件下30 r/min時主動輪磨損厚度

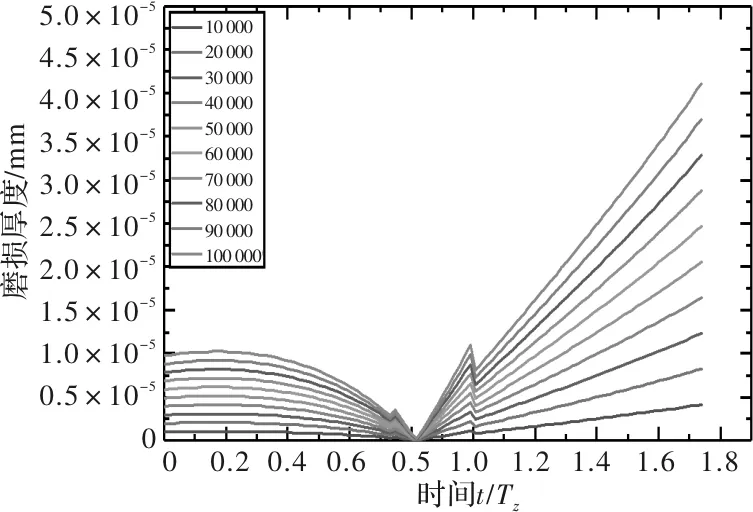
圖17 準靜態條件下50 r/min時主動輪磨損厚度

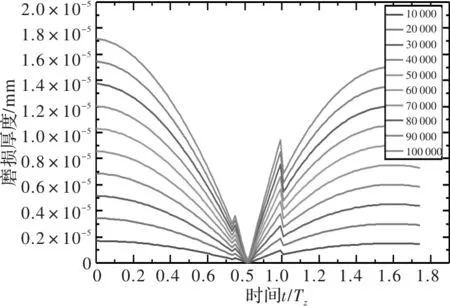
圖18 準靜態條件下50 r/min時主動輪磨損厚度

圖13～圖18中分別給出了主動輪和從動輪在10 r/min、30 r/min和50 r/min轉速下，嚙合次數分別為10 000，20 000，…，100 000時的齒面磨損厚度。可以看出，王曉筍等人計算齒面磨損分布時，在節線處齒輪磨損厚度同樣為零，齒面磨損厚度隨著齒輪節線距離增加而增加，但是在齒輪嚙合力突變處能看出有明顯突變。從動輪在進入嚙合段的磨損較大，而主動輪在進入與退出嚙合段的磨損較為均衡。可以看出準靜態齒輪齒面磨損計算無法反映出齒輪的動態特性。

5 結論

本文利用Archard粘著磨損理論，并結合最小勢能理論計算低速重載齒輪在轉速變化時的齒輪齒面嚙合力變化規律，同時計算出在變載荷條件下的齒輪磨損厚度變化。隨著轉速升高，齒輪齒面動態嚙合力逐漸趨于平穩，齒面沖擊減弱。通過對比準靜態齒輪齒面磨損計算方法，可以看出需要充分結合齒輪的動態特性并計算齒面磨損分布，齒輪齒面動態嚙合力變化是導致齒齒面磨損分布變化的主要原因。