基于反步自適應控制算法的船舶航向控制方法
安 順,何 燕,王龍金
(青島科技大學 機電工程學院,山東青島266061)
0 引言
傳統船舶航向控制器通常采用一階野本模型[1](Nomoto線性模型),但由于船舶航行具有大慣性、非線性和大時滯性的特點,同時受風、浪、流等環境因素的干擾作用,使得船舶運動模型具有不確定性和非線性的特性。反步法,又稱反演法(Back-stepping),它的基本思想是對復雜的非線性系統進行分解,使得子系統的階數小于系統階數,然后為每個子系統設計Lyapunov函數和中間變量,通過“反演”后退到整個系統,最后將所有子系統集成起來完成整個系統的控制率設計[2]。自上世紀90年代,KOKOTOVIC[3]等率先提出反步法并應用于控制器設計,使得對非線性系統的控制更加廣泛化,之后各國學者又對該方法不斷發展。陳佳偉[4]采用反步自適應法對模型不確定性、輸入飽和以及外部干擾分別設計了控制器,并取得了較好的仿真結果。BENASKEUR等[5]將反步法應用到自適應PID控制當中,通過加入一個積分作用,克服了基于確定性等價原理PID控制沒有考慮動態性自適應的問題,使得PID控制更具有魯棒性。
Lyapunov穩定性理論是先進控制理論研究非線性系統最一般的理論,是現代控制理論的基礎。它是由蘇聯數學家LYAPUNOV A M[6]在1982年提出,Lyapunov穩定性理論主要有兩種分析方法(直接法和間接法),間接法是通過對非線性系統的線性化分析系統在平衡點的局部穩定性,直接法是通過構造一個“能量型函數(V型函數)”,研究該函數隨時間的變化分析系統的穩定性。隨著計算機水平的提高,由此理論發展出一系列對非線性系統的先進控制方法,并且和智能控制相結合,如模糊自適應控制、神經網絡自適應控制、滑模控制等等[7],使得非線性系統控制器的設計更具有魯棒性。
本文深入研究了船舶航向自適應反步控制器設計方法,以含有未知非線性項參數的船舶數學模型為研究對象,設計了一種基于反步法的自適應船舶航向控制器,并通過Matlab對控制系統進行仿真試驗。仿真試驗結果表明,所設計的控制器具有良好的控制性能。
1 船舶數學模型的建立
1.1 Norrbin非線性數學模型
傳統一階Nomoto模型只適用于小擾動情況,但在實際情況中,當船舶受到較大擾動時則必須采用非線性模型才能準確描述船舶的運動狀態。Norrbin在1963年提出了船舶運動非線性數學模型[8]

式中:T和K為船舶操縱特性指數,與船型、裝載及航速有關;r為航向角速度;α為未知Norrbin系數,在設計控制器時假設T、K和α均為未知參數;δ為輸入舵角。
選取狀態變量1x φ= ,2x r φ= = ˙,u δ= ,φ是航向角,得到含有未知參數的單輸入單輸出船舶航向非線性數學模型,即
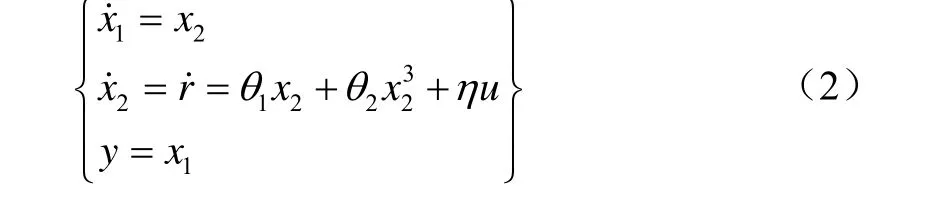
式中:θ1=?1/T;θ2=?α/T;η=?K/T。
1.2 舵機特性計算模型
由于舵機伺服系統具有飽和、延遲及死區等非線性特性,使得船舶舵機系統不能實現階躍性操舵,如果忽略舵機特性,會對船舶航向控制系統產生較大的影響[9]。為使船舶航向控制系統控制效果逼近真實操舵效果,應當充分考慮舵機伺服系統的特性。通常,船舶舵機特性用一階慣性模型表示,即

2 反步自適應船舶航向控制器設計
針對含有未知參數的非線性船舶運動數學模型,采用反步法和Lyapunov直接方法設計船舶航向自適應控制器,控制器的目標是尋找一個控制律u=δ,使得船舶實際航向φ能夠良好的跟蹤給定的期望航向φd。




3 實驗及仿真結果
本文以大連海事大學的教學實習船“育龍”輪[12]為對象進行仿真研究,以驗證本文反步自適應控制器的有效性。該船的相關模型參數為:K=0.478,T=216,非線性系數α3=30s2。參數K1、K2和ρ可以在保證系統穩定的前提下取為常數,這里取為K1=1,K2=50,ρ=15,λ1和λ2為自適應參數增益,與參數更新的速率有關,對控制效果影響不大,在保證控制器收斂的情況下,取λ1=λ2=0.05。圖1為控制系統的仿真流程圖,在Simulink中進行建模,設定指令航向為10°,航向角和指令舵角的變化曲線如圖2和圖3所示,航向誤差差變化曲線如圖4所示。
由圖2可知,船舶實際航向x1能夠快速平滑跟蹤給定的參考航向x1d,沒有超調,控制效果良好。從圖3可知,指令舵角δ在經歷短暫滿舵后快速衰減,而后平滑的增加,最終趨于0,控制舵角變化合理。圖4說明航向誤差快速衰減為0,最終達到0誤差,即完全跟蹤指令航向。
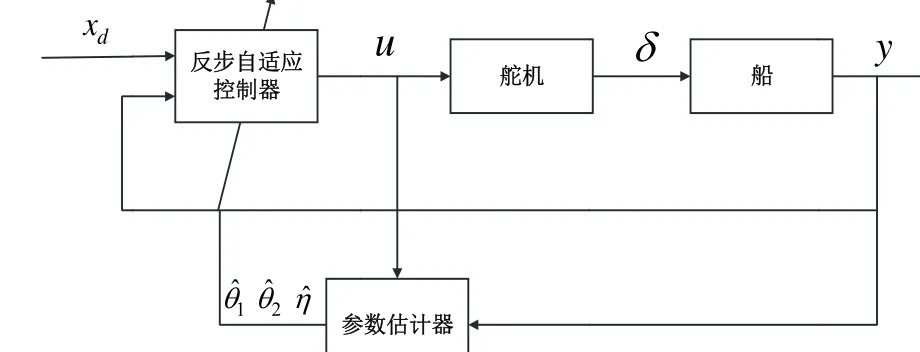
圖1 反步自適應仿真流程圖
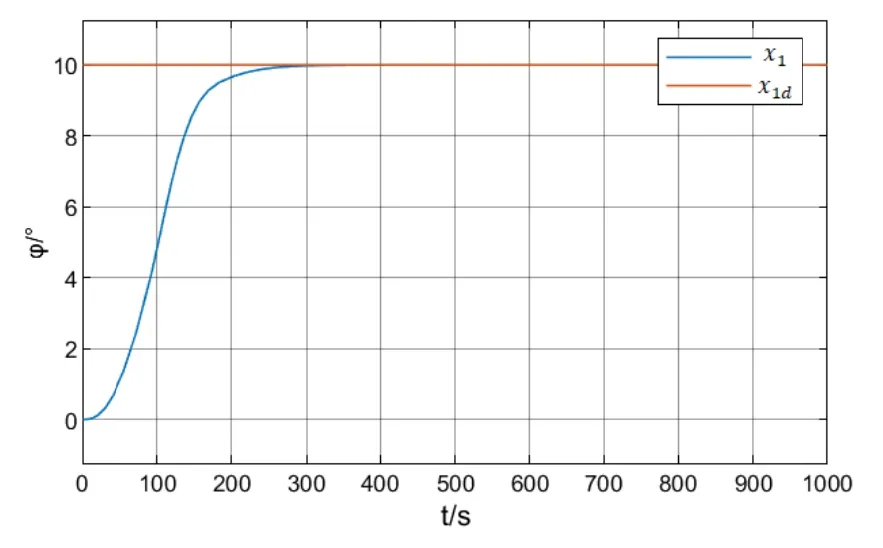
圖2 船舶航向變化曲線
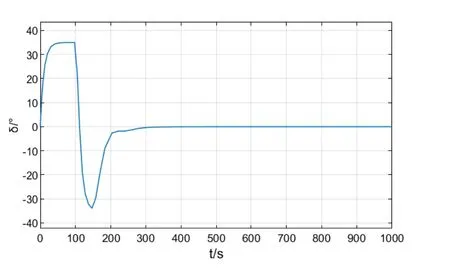
圖3 輸入舵角變化曲線
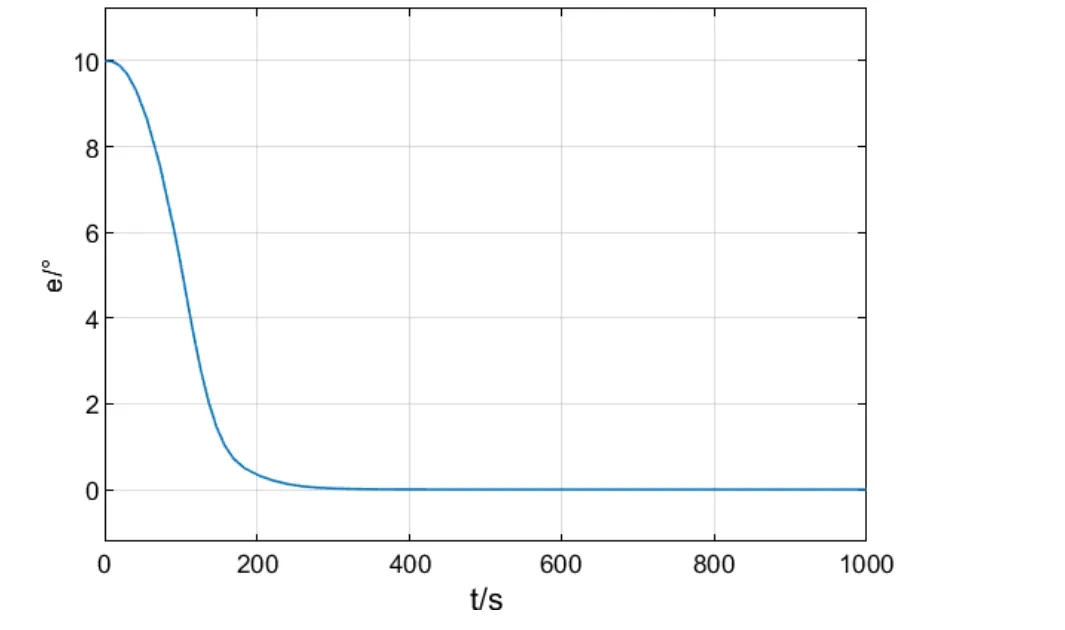
圖4 航向誤差變化曲線
4結論
針對船舶運動數學模型的不確定性和非線性特性,本文設計了基于反步法的自適應航向控制系統,并在Simulink 中進行仿真試驗。仿真試驗表明,在給定期望參考輸入信號的情況下,控制器能夠良好的跟蹤參考信號,證明本文設計的控制器是合理有效的。

