基于灰色關聯模型的針織物熱濕舒適性分析與預測

王麗莎，馬曉紅，孟 花，馮愛芬

(1.河北科技大學 紡織服裝學院，河北 石家莊 050018； 2.河北省紡織服裝技術創新中心，河北 石家莊 050018)

熱濕舒適性指人體在變化的環境中通過熱濕傳遞的作用獲得舒適滿意度的感覺[1]。織物在人體和環境之間形成一個微小氣候區作為人體與外界環境熱濕傳遞的中間物，直接影響二者之間的熱濕交換，從而影響人體的熱濕舒適感。織物的熱濕舒適性是一個物理學和生理學的綜合問題，是評判服用性能的重要組成部分[2-3]。灰色模型(Grey Model，簡稱GM)是多變量灰色系統建模方法的基本模型，該模型中包含多個影響因子變量，常用于分析多個影響因子變量對系統行為變量的作用，來確定該系統未來發展的變化趨勢，為規劃、決策提供依據[4-5]。本文主要運用灰色模型預測針織物的熱濕舒適感覺，將織物所測得可能影響織物熱濕舒適性的10個指標看作一個灰色系統，運用灰色關聯分析法處理數據，計算出10個指標與熱濕舒適性加權分值之間的關聯程度，確定每個熱濕指標的權重系數，最后建立熱濕舒適性灰色模型并進行預測。

1 試驗部分

1.1 試驗材料

由河北吉篙化纖有限責任公司提供的7種針織物作為研究對象，織物中所含艾草改性竹漿纖維和竹漿纖維均為河北吉篙化纖有限責任公司生產。已知紗線原料成分、紗線細度、織物組織，測試了針織物密度、面密度和厚度，其基本規格見表1。

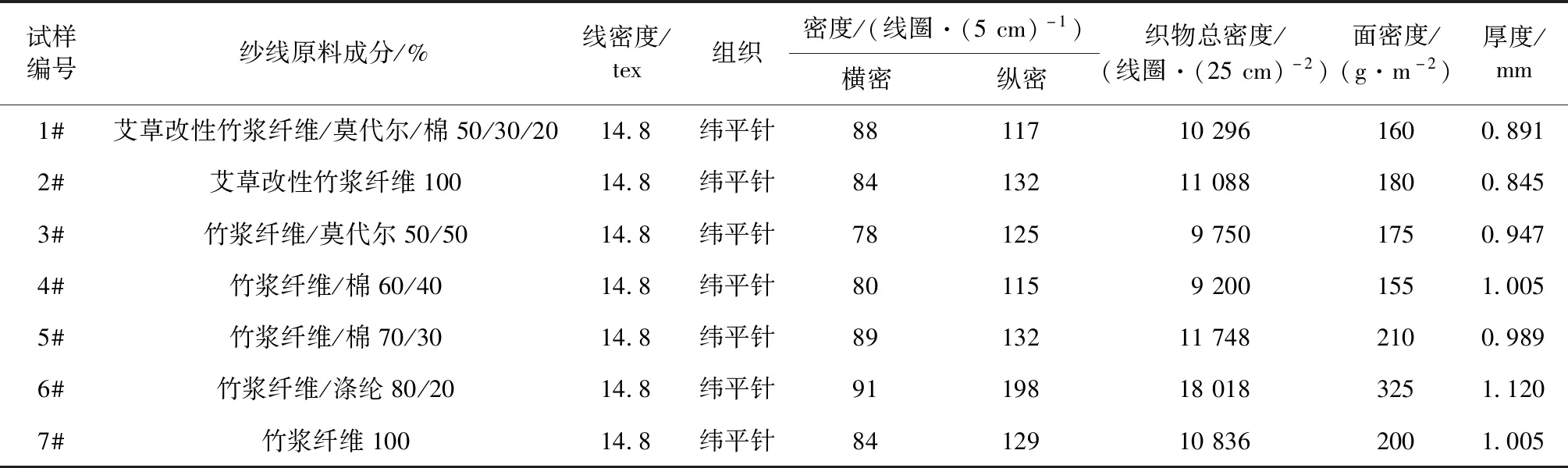
表1 織物規格及結構參數

1.2 織物導熱性和接觸冷暖感性能測定

采用KES-F7測試儀(日本加多技術有限公司)測試織物的熱傳導系數和瞬間冷暖感，參照儀器的試驗方法，將織物裁剪為20 cm×20 cm，試驗前將裁剪好的試樣放入恒溫恒濕室平衡24 h，在恒溫恒濕的條件下進行測試，每種織物測試3次，取其平均值。

1.3 織物透氣性測定

采用YG461E型數字式透氣量儀(寧波紡織儀器廠)，參照GB/T 5453—1997《紡織品 織物透氣性的測定》,將織物裁剪為30 cm×30 cm，試驗前將裁剪好的試樣放入恒溫恒濕室平衡24 h，試驗面積為20 cm2,壓強100 Pa，每種織物不同部位測試10次，取其平均值。

1.4 織物透濕性能測定

采用YG601型電腦式織物透濕儀(寧波紡織儀器廠)，參照GB/T 12704.2—2009《紡織品 織物透濕性試驗方法 第2部分：蒸發法》，將織物裁剪為直徑7 cm的圓形試樣，試驗溫度37 ℃，相對濕度50%，時間1 h，每種織物測試3次，取其平均值。

1.5 織物回潮率性能測定

采用Y(B)802G型八籃恒溫烘箱(溫州大榮紡織儀器有限公司)，將織物裁剪為30 cm×30 cm，試驗前將裁剪好的試樣放入恒溫恒濕室平衡24 h達到吸濕平衡并稱量，質量記為G，再將試樣放入105 ℃的烘箱中放置2 h，記錄質量為G0，按式(1)計算織物回潮率W，每種織物測試3次，取其平均值。

(1)

式中，W為紡織材料的回潮率，%；G為紡織材料的濕質量，g；G0為紡織材料的干質量，g。

1.6 織物導水性能測定

采用YG(B)871型毛細管效應測定儀(溫州大榮紡織標準儀器廠)，參照FZ/T 01071—2008《紡織品 毛細效應試驗方法》,將織物裁剪為250 mm×30 mm，橫向和縱向各3塊，試驗前將裁剪好的試樣放入恒溫恒濕室平衡24 h，水溫27 ℃，記錄30 min后液體沿試樣上升的高度值。

1.7 主觀服裝熱濕舒適性測定

將7種面料分別制成160/84 A同一款式同一規格的普通無袖運動背心，挑選14名紡織服裝專業女生，年齡為(23±2)歲，體重為(50±3)kg,身高、體重都符合GB/T 1335.2—2008《服裝號型 女子》女性的標準中較為普遍的Y體160/84A的要求。試驗前將服裝放置在恒溫恒濕的壞境中平衡24 h。測試條件：溫度為35～37 ℃，相對濕度46%～50%，運動15 min，運動結束后在恒溫恒濕的環境中休息10 min后進行熱濕舒適性評分，最小值評分值為0，最大值評分值為100。

2 試驗結果與分析

2.1 試驗測試結果

根據前文方法對試樣進行測試，試驗測試結果如表2所示。由表可知，織物在各方面的性能優劣不同，很難根據某一項具體指標作整體熱濕舒適性評價。此外，由于數據規律分布不明顯并且數據量少，用傳統的確定性數學進行分析很難得出有效的結論。因此，本文引用模糊數學中的灰色理論系統建立灰色關聯模型更好的預測針織物的熱濕舒適性感覺。

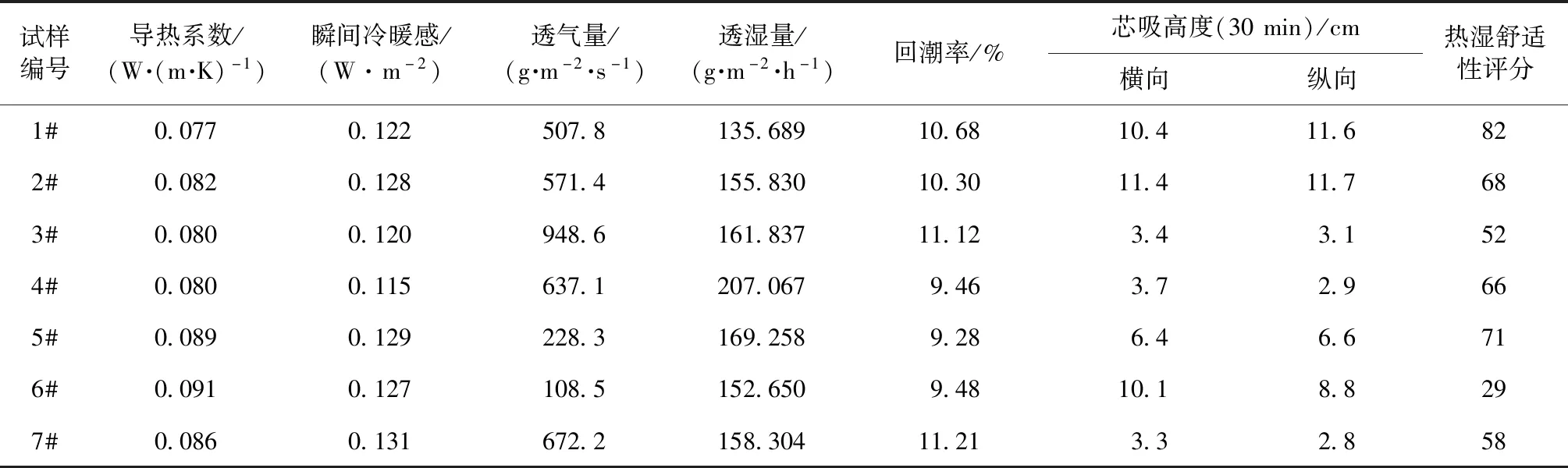
表2 織物熱濕性能測試值

2.2 灰色關聯分析

2.2.1 灰色關聯度

灰色關聯分析的原理是根據序列曲線幾何形狀的相似程度來判斷其關系是否緊密，曲線越接近，相應序列之間的關聯度就越大，反之就越小[6]。

設x0=(x0(1),x0(2),…,x0(n))={x0(k)|k=1,2,…，n}為系統參考序列，xi=(xi(1),xi(2),…,xi(n))={xi(k)|k=1,2,…，n}(i=1,2,…,m)為比較序列。而灰色綜合關聯度即體現了折線x0和xi的相似程度，又能反應x0與xi相對于始點的變化速率的相近程度，是一個較為全面地表征序列之間聯系是否緊密的量。灰色綜合關聯度求解過程如下[7]：

均值化：

(2)

求差序列：

(3)

求兩級差：

m=minimink|x0(k)-xi(k)|為兩級最小差，M=maximaxk|x0(k)-xi(k)|為兩級最大差。

求關聯系數：

(4)

式中ρ為分辨系數，ρ∈(0,1)，本文取ρ=0.5。

求關聯度ri：

(5)

ri反映了比較數列xi與參考數列x0的相關程度，ri值越大，表示二者的關系越密切，說明比較數列xi對參考數列x0的影響因素越大[8]，通過灰色關聯度分析，找出對織物熱濕舒適性影響程度大的因素作為主要因子。

2.2.2 關聯度求解

將針織物的基本參數、物理指標看作一個灰色系統，熱濕舒適性加權評分分別為參考數列，記X0=(x0(1),x0(2),…,x0(7))針織物的基本性能與物理性能為比較數列，記Xi=(xi(1),xi(2),…,xi(7))，i=1,2,3，…，10，即X1為總密度，X2為面密度，X3為厚度，X4為導熱系數，X5為瞬間冷暖感，X6為透氣量，X7為透濕量，X8為回潮率，X9為橫向芯吸高度，X10為縱向芯吸高度。由式(2)～(5)計算關聯系數和關聯度，計算結果見表3。

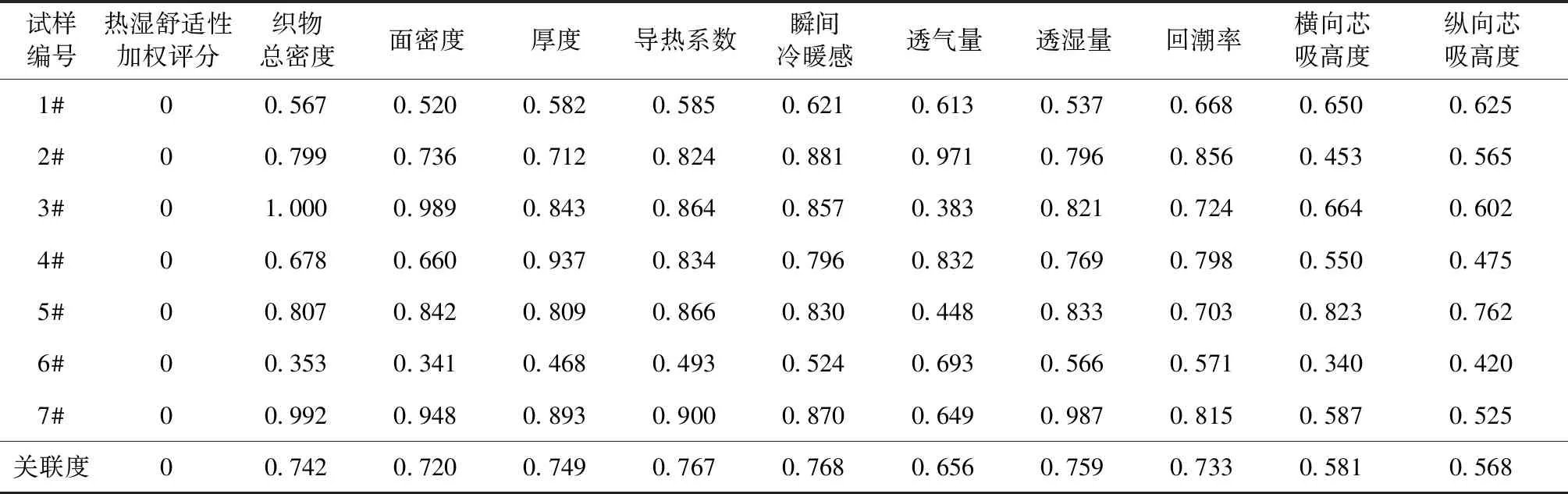
表3 關聯系數和關聯度

從表3可以得出，面料性能與熱濕舒適性之間的關聯度大小排序：瞬間冷暖感>導熱系數>透濕量>厚度>織物總密度>回潮率>面密度>透氣量>橫向芯吸高度>縱向芯吸高度。根據表3可知，7種針織物各熱濕舒適性之間的關聯度均在0.55以上，表示這10個性能指標均可在某種程度上影響針織物的熱濕舒適性。為了更好地研究針織物的性能與熱濕舒適性之間的關系，將排名前4位的看作是預測模型中的主要影響因素，因此關聯系數較大的熱濕舒適性能因素依次為瞬間冷暖感、導熱系數、透濕量、厚度。

2.3 針織物性能的灰色關聯模型

針織物的熱濕舒適性受多個指標的影響，而在灰色系統模型中GM (1,N)模型適用于對多數組變量的預測，因此可用GM (1,N)模型進行針織物熱濕舒適性預測。

2.3.1 GM(1,N)模型理論分析

由上述對針織物性能與熱濕舒適性的關聯度求解可知，熱濕舒適性與瞬間冷暖感、厚度、回潮率、透濕量相關，通過使用灰色預測理論建立GM (1,N)模型來實現針織物熱濕舒適性之間的預測，建模步驟如下[8]:

① GM (1,N)模型是由N個變量組成的一階線性動態模型，其微分方程為：

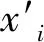
(6)

其中

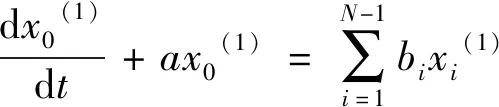
(7)

(8)

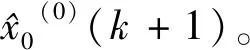
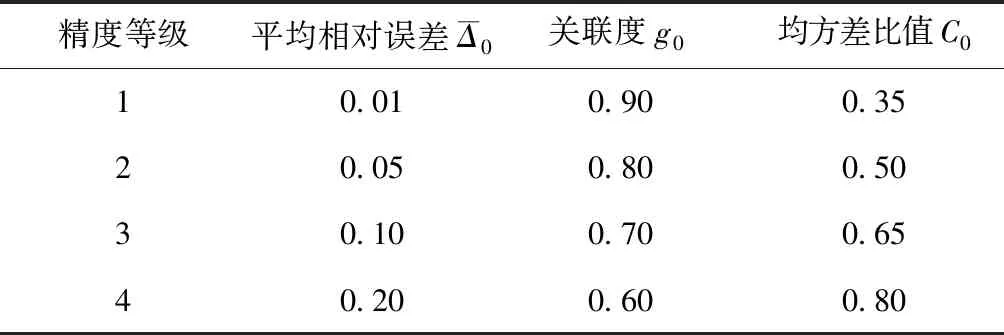
表4 灰色模型預測精度等級標準

2.3.2 建立熱舒適性預測模型

原始數據序列為Xi={xi(1)，xi(2)，…，xi(n)}，其中i=0，1，2，3，4,n=1，2，3，…，7，X0=熱濕舒適性加權分值，X1=厚度，X2=導熱系數，X3=瞬間冷暖感，X4=透濕量，生成序列見表5。

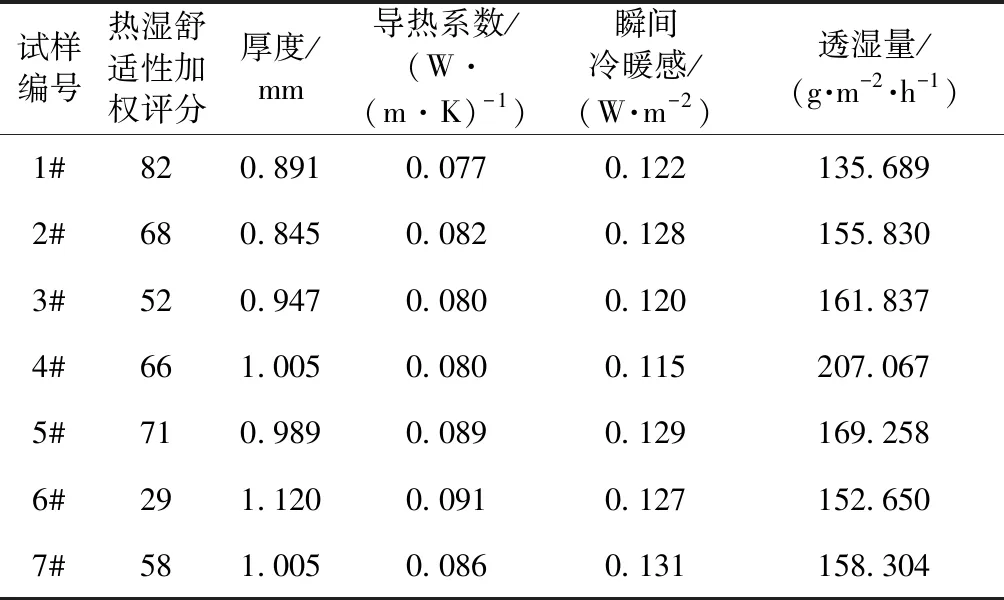
表5 生成序列

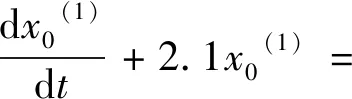
3 869.8x3(1)+1.2x4(1)

(9)

由式(7)可得GM(1, 5)模型的解為：

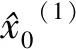
(10)

模型精確度驗證：分別取k=0,1,2，…，6。結合式(8)和式(10)計算得到模型殘差檢驗的各項指標見表6。

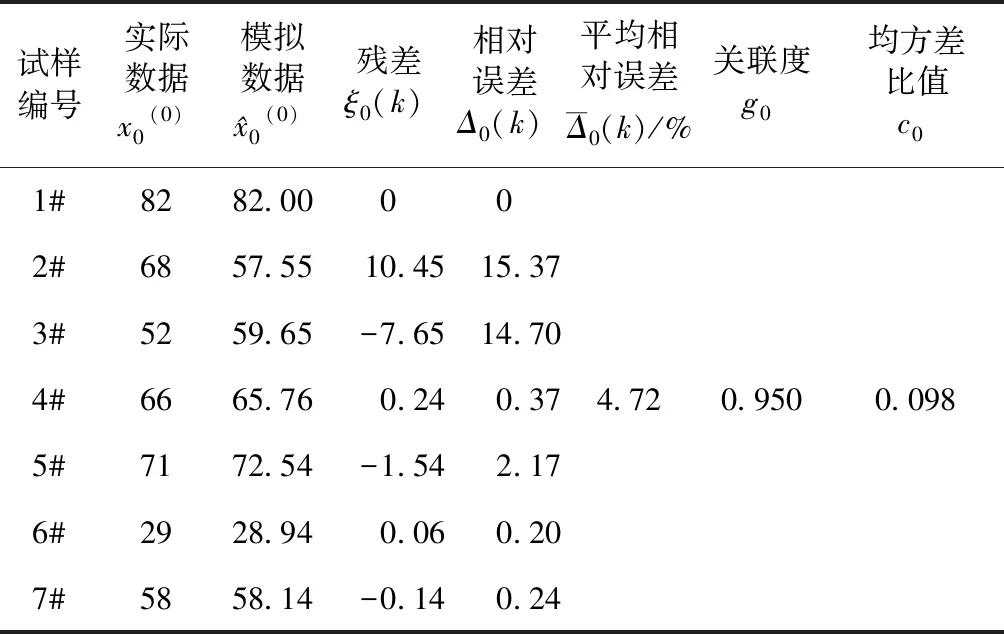
表6 殘差檢驗

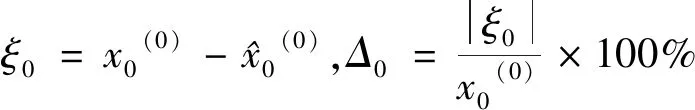
由表6可知模型模擬值與實際值比較接近。相對誤差控制在5%以內的有5個，占總體的71.43%；控制在5%～15%之間的有2個，占總體的28.57%。根據表4灰色模型預測精度等級標準平均相對誤差為4.72%，大于二級精度；關聯度為0.950，為一級精度；均方差比值為0.098，為一級精度，表明此模型模擬數據與實際數據具有較高的相關度。

2.4 模型應用

對艾草改性竹漿纖維/滌綸(84/16)面料進行測試，測試結果見表7。

表7 織物測試數據

取k=0，將表7中的織物測試參數分別代入式(10)計算得出織物的熱濕舒適性評分為63.88。由此可知此織物熱濕舒適性相對較好，可以應用于服裝中，為消費者提供更多的選擇。

3 結 論

通過灰色關聯度分析，結果顯示織物性能與熱濕舒適性之間的關聯度大小依次為瞬間冷暖感、導熱系數、透濕量、厚度、織物總密度、回潮率、面密度、透氣量、橫向芯吸高度、縱向芯吸高度。

對影響因素較大的影響因子瞬間冷暖感、導熱系數、透濕量、厚度與熱濕舒適性建立了GM(1, 5)關聯模型，模型與實際預測值具有較高的相關度，從而在得知織物的瞬間冷暖感、導熱系數、透濕量、厚度的情況下實現對織物熱舒適性的預測分析，節省了試驗量，提高了工作效率。