基于非監(jiān)督貝葉斯學(xué)習(xí)雷達(dá)性能指標(biāo)動(dòng)態(tài)評(píng)估

楊 磊, 毛欣瑤, 楊曉煒, 張 海, 楊 菲, 孫 麟

(1. 中國(guó)民航大學(xué)天津市智能信號(hào)與圖像處理重點(diǎn)實(shí)驗(yàn)室, 天津 300300;2. 中國(guó)工程物理研究院電子工程研究所, 四川 綿陽(yáng) 621999)

0 引 言

在雷達(dá)領(lǐng)域,除了研究先進(jìn)的系統(tǒng)集成工藝和信號(hào)處理算法外,針對(duì)雷達(dá)系統(tǒng)性能指標(biāo)的評(píng)估也是重要的研究方向[1-2]。尤其在雷達(dá)工作面臨的目標(biāo)特性和電磁環(huán)境日益復(fù)雜的情況下,研究各種因素動(dòng)態(tài)演化過(guò)程中雷達(dá)系統(tǒng)性能指標(biāo)的變化趨勢(shì),為優(yōu)化雷達(dá)系統(tǒng)性能提供重要的參考,對(duì)提升雷達(dá)系統(tǒng)實(shí)際工作效能具有重要的現(xiàn)實(shí)意義。傳統(tǒng)的雷達(dá)系統(tǒng)性能指標(biāo)評(píng)估方法大多是靜態(tài)的,在固定目標(biāo)特性和電磁干擾環(huán)境后,計(jì)算雷達(dá)系統(tǒng)相關(guān)性能指標(biāo),從而獲取系統(tǒng)性能指標(biāo)。這樣的方法對(duì)系統(tǒng)真實(shí)工作效能的反映相對(duì)單一,難以體現(xiàn)系統(tǒng)動(dòng)態(tài)演化的目標(biāo)特性和電磁干擾環(huán)境中的真實(shí)工作表現(xiàn),指示作用有限且實(shí)際應(yīng)用存在局限性。

傳統(tǒng)的動(dòng)態(tài)評(píng)估方法大多是基于中心極限定理的蒙特卡羅(Monte Carlo,MC)[3]方法,該方法通過(guò)多次重復(fù)一定實(shí)驗(yàn)環(huán)境來(lái)計(jì)算指標(biāo)值,再通過(guò)多次的實(shí)驗(yàn)數(shù)值結(jié)果計(jì)算統(tǒng)計(jì)均值和方差,從而確定指標(biāo)的估計(jì)值及其變化范圍。然而,這種評(píng)估方法存在一定的局限性。首先,評(píng)估方法相對(duì)機(jī)械,需要遍歷全部可能的目標(biāo)特性或環(huán)境參數(shù)才能獲得評(píng)估結(jié)果;其次,評(píng)估結(jié)果指示意義有限,根據(jù)MC方法獲得的統(tǒng)計(jì)均值和方差僅能表示一定條件下多次重復(fù)實(shí)驗(yàn)的收斂性,擴(kuò)展性有限,理論指示意義一般,無(wú)法給出定量的約束表達(dá)式;最后,該方法的精度嚴(yán)重依賴于實(shí)驗(yàn)次數(shù),因此評(píng)估效率較低,評(píng)估成本較高。

針對(duì)MC方法的局限性,業(yè)界展開(kāi)了廣泛的研究,主要包括定性法[4]、定量法[5-6]及定性定量結(jié)合法[7]。定性法簡(jiǎn)單易懂,可操作性強(qiáng),但是具有很強(qiáng)的主觀性,應(yīng)用效果受外界影響較大,無(wú)法進(jìn)行定量評(píng)估;定量法原理清晰,客觀性強(qiáng),但是該方法大多忽略了已有的先驗(yàn)知識(shí),只適用于仿真數(shù)據(jù)和參考數(shù)據(jù)均存在的情況,擴(kuò)展性有限,指示意義較差;定性定量結(jié)合法將定性法和定量法所得信息加以綜合,發(fā)揮定性和定量方法的優(yōu)勢(shì),可對(duì)仿真系統(tǒng)的可信度進(jìn)行整體判斷,但是其在仿真系統(tǒng)具體考察方面以及綜合不同方面獲取信息上并沒(méi)有形成統(tǒng)一的結(jié)論,現(xiàn)實(shí)意義反映能力一般。因此,探索一種指示意義以及現(xiàn)實(shí)反應(yīng)能力強(qiáng)的評(píng)估方法很有必要的。

綜上所述,現(xiàn)有的雷達(dá)系統(tǒng)性能評(píng)估方法大多是基于靜態(tài)指標(biāo)評(píng)估準(zhǔn)則的,即設(shè)計(jì)性能指標(biāo)難以反映系統(tǒng)環(huán)境變化以及系統(tǒng)存在誤差情況下的動(dòng)態(tài)性能,實(shí)際參考價(jià)值有限。因此,有必要研究針對(duì)雷達(dá)系統(tǒng)性能指標(biāo)的動(dòng)態(tài)評(píng)估方法。本文采用貝葉斯學(xué)習(xí)的方法來(lái)實(shí)現(xiàn)雷達(dá)系統(tǒng)性能指標(biāo)的動(dòng)態(tài)評(píng)估,利用其提供的指標(biāo)解析后驗(yàn)概率密度函數(shù),獲得待評(píng)估指標(biāo)的期望及方差等高階統(tǒng)計(jì)量,從而可獲得可靠的指標(biāo)估計(jì)值及置信區(qū)間,進(jìn)而實(shí)現(xiàn)對(duì)系統(tǒng)性能指標(biāo)的動(dòng)態(tài)評(píng)估,此方法最大的優(yōu)點(diǎn)是只需要一次觀測(cè)數(shù)據(jù)便可以獲得解析的指標(biāo)評(píng)估結(jié)果,指示物理意義明確。本文在實(shí)驗(yàn)中改變不同的參數(shù)及仿真環(huán)境,通過(guò)與傳統(tǒng)MC方法評(píng)估結(jié)果做對(duì)比,定量和定性地分析了非監(jiān)督貝葉斯學(xué)習(xí)在雷達(dá)性能指標(biāo)評(píng)估上的優(yōu)勢(shì),并驗(yàn)證了所提方法的穩(wěn)健性、高效性及通用性。

1 回波信號(hào)模型

通常的,雷達(dá)目標(biāo)探測(cè)系統(tǒng)回波數(shù)據(jù)可以建模為

Y=EAXB⊙F+C+N+I

(1)

式中，Y∈CN×M表示接收雷達(dá)目標(biāo)探測(cè)數(shù)據(jù),可以是一維單脈沖數(shù)據(jù),也可以是二維多脈沖數(shù)據(jù),如合成孔徑雷達(dá)(synthetic aperture radar, SAR)成像回波數(shù)據(jù),N和M分別表示方位向和距離向的采樣點(diǎn)數(shù);X∈CN×M表示探測(cè)結(jié)果或待評(píng)估性能指標(biāo)變量;A和B分別表示方位向和距離向傅里葉變換或匹配濾波字典,主要作用是完成二維成像壓縮處理;E表示方位向時(shí)變誤差字典,如SAR成像過(guò)程中可能存在的相位誤差,根據(jù)相位誤差的非空變特性,可建模為對(duì)角矩陣,對(duì)角線上的元素對(duì)應(yīng)相應(yīng)方位時(shí)刻的相位誤差;⊙表示Hadamard積;F表示越距離單元徙動(dòng)校正字典或包絡(luò)誤差校正字典;C表示背景雜波;N表示系統(tǒng)熱噪聲;I表示有意或無(wú)意的干擾。

式(1)可以描述典型雷達(dá)探測(cè)系統(tǒng)的回波數(shù)據(jù)模型[8],該模型適用范圍廣,適用性強(qiáng)，既可以兼容非建模誤差,又可以兼容噪聲、干擾、雜波等加性誤差。其中方位相位誤差(azimuthal phase error,APE)和非系統(tǒng)性距離單元徙動(dòng)(nonsystematic range cell migration,NsRCM)誤差分別在E和F中表示,基于非監(jiān)督貝葉斯學(xué)習(xí)的雷達(dá)性能指標(biāo)動(dòng)態(tài)評(píng)估的標(biāo)準(zhǔn)即為評(píng)估E、C、N、I對(duì)X的影響。

2 雷達(dá)性能指標(biāo)貝葉斯建模

2.1 目標(biāo)指標(biāo)先驗(yàn)概率模型

本文研究針對(duì)典型雷達(dá)探測(cè)系統(tǒng)性能指標(biāo)評(píng)估問(wèn)題,應(yīng)用貝葉斯學(xué)習(xí)方法,引入目標(biāo)指標(biāo)先驗(yàn)概率分布,并考慮環(huán)境統(tǒng)計(jì)分布,從而獲取指標(biāo)后驗(yàn)概率分布估計(jì),實(shí)現(xiàn)對(duì)性能指標(biāo)的動(dòng)態(tài)變化區(qū)間估計(jì)。因此,首先需要對(duì)典型性能指標(biāo)或雷達(dá)目標(biāo)探測(cè)結(jié)果施以合適的先驗(yàn)概率分布。

雷達(dá)目標(biāo)探測(cè)系統(tǒng)中,目標(biāo)相對(duì)背景環(huán)境滿足稀疏性特征,比如對(duì)空探測(cè)雷達(dá),感興趣的目標(biāo)相對(duì)于天空背景雜波是稀疏的;地面運(yùn)動(dòng)目標(biāo)檢測(cè)中,動(dòng)目標(biāo)相對(duì)地面背景雜波是稀疏的。此時(shí)可以對(duì)相關(guān)目標(biāo)特征施加稀疏先驗(yàn),或?qū)ο鄳?yīng)性能指標(biāo)施加稀疏性特征。從概率的角度描述稀疏特征,通常可以將待估計(jì)(隨機(jī))變量的先驗(yàn)概率分布建模為重尾的概率分布,而Laplace分布為典型的重尾先驗(yàn)分布,其表示為

(2)

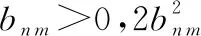
2.2 目標(biāo)探測(cè)數(shù)據(jù)似然函數(shù)模型

在完成對(duì)待評(píng)估指標(biāo)X的先驗(yàn)建模后,需要對(duì)接收雷達(dá)目標(biāo)探測(cè)數(shù)據(jù)Y建立概率模型,即建立Y的似然函數(shù)模型,考慮典型雷達(dá)探測(cè)系統(tǒng)觀測(cè)數(shù)據(jù)存在誤差,比如系統(tǒng)熱噪聲、探測(cè)系統(tǒng)電磁環(huán)境動(dòng)態(tài)演化、背景雜波等都會(huì)影響目標(biāo)探測(cè)數(shù)據(jù)的準(zhǔn)確性,因此有必要對(duì)這些誤差建模分析。

系統(tǒng)熱噪聲通常可以直接利用零均值的高斯分布進(jìn)行統(tǒng)計(jì)建模。當(dāng)環(huán)境電磁干擾為隨機(jī)變量時(shí),比如壓制式干擾,由于其造成的影響主要是導(dǎo)致回波信干比升高,因此可將其建模為類高斯分布;當(dāng)雜波為均勻雜波時(shí),可用高斯分布進(jìn)行統(tǒng)計(jì)描述。因此,將噪聲、干擾、雜波這些測(cè)量誤差假設(shè)成高斯模型是合理的,對(duì)于非高斯分布的模型,可通過(guò)混合高斯模型進(jìn)行假設(shè),即利用多個(gè)參數(shù)不同的高斯分布混合建立成一個(gè)相對(duì)復(fù)雜的概率分布[9]。所以,雷達(dá)目標(biāo)探測(cè)數(shù)據(jù)似然函數(shù)模型為

(3)

式中，β=[β1,β2,…,βM],表示每個(gè)距離單元對(duì)應(yīng)的加性誤差干擾的精度,βm表示第m個(gè)距離單元的精度;對(duì)應(yīng)高斯分布中方差的倒數(shù)CN(·)代表復(fù)高斯分布;Y:m表示接收雷達(dá)目標(biāo)探測(cè)數(shù)據(jù)的第m列;X:m表示該評(píng)估性能指標(biāo)變量的第m列，I0表示單位對(duì)角矩陣。

2.3 貝葉斯分層概率模型

基于上面建立的性能指標(biāo)先驗(yàn)概率模型和回波數(shù)據(jù)似然函數(shù)模型,便可以在貝葉斯推論下獲取指標(biāo)后驗(yàn)概率密度函數(shù)估計(jì)。然而,擬建立的稀疏Laplace先驗(yàn)分布與高斯似然函數(shù)非共軛,無(wú)法獲得后驗(yàn)分布的有效閉合解,因此本文運(yùn)用貝葉斯分層概率模型,針對(duì)非高斯的Laplace先驗(yàn)概率模型建立貝葉斯分層概率模型[10-11],通過(guò)引入中間超參數(shù)分層建立概率模型,來(lái)保證后驗(yàn)概率密度函數(shù)的可解性。

在層次結(jié)構(gòu)的第一層[12-13],將待評(píng)估指標(biāo)X建模為多變量聯(lián)合高斯分布

(4)

式中，Λm=diag(α:m)為超參數(shù)矩陣α的第m列所組成的對(duì)角矩陣,即為X:m的協(xié)方差矩陣,Λm相互獨(dú)立。在第二層,超參數(shù)α被建模為服從參數(shù)η和λ的Gamma分布[12-13]，可表示為

(5)

然而,剩余的超參數(shù)λ維度較高,容易導(dǎo)致計(jì)算結(jié)果過(guò)擬合。因此,針對(duì)λ再次引入Gamma分布進(jìn)行第三層分層建模[14]，可表示為

(6)

式中，a和b為常數(shù),根據(jù)經(jīng)驗(yàn)值可取10-6。

此外,為了建立更加實(shí)用的貝葉斯模型,最后考慮對(duì)觀測(cè)誤差精度β建立服從Gamma分布的概率模型如下：

(7)

式中，c和d為常數(shù),根據(jù)經(jīng)驗(yàn)值可取10-6。觀察如式(7)所示的概率模型可見(jiàn),針對(duì)不同距離單元的噪聲精度建立概率模型,并在后續(xù)貝葉斯中實(shí)現(xiàn)推理,可以保證對(duì)不同距離單元的誤差進(jìn)行差異化建模,精度更高。

3 指標(biāo)的后驗(yàn)概率密度函數(shù)求解

根據(jù)第2.3節(jié)給定的貝葉斯分層概率模型,直接應(yīng)用貝葉斯推論計(jì)算目標(biāo)探測(cè)結(jié)果或待評(píng)估性能指標(biāo)變量X和超參數(shù)α,λ,β的聯(lián)合后驗(yàn)分布為

(8)

式中，等號(hào)右側(cè)分子項(xiàng)已由式(3)～式(7)分別給出。但是為了得到分母項(xiàng),需要對(duì)公式的分子項(xiàng)進(jìn)行高維積分如下：

p(α|λ)p(λ)p(β)dβdλdαdX

(9)

然而,求解式(9)的多重積分在實(shí)際中難以實(shí)現(xiàn),因此必須借助有效的求解算法。

常規(guī)地,求解如式(8)所示的聯(lián)合后驗(yàn)分布的方法可分為兩類:近似確定性算法和統(tǒng)計(jì)采樣算法。其中，變分貝葉斯期望最大化(variational Bayesian expectation maximization,VB-EM)[15]作為一種典型的近似確定性算法,可有效實(shí)現(xiàn)隱隨機(jī)變量推理,并通過(guò)期望最大化步驟獲得隨機(jī)變量后驗(yàn)分布解析解和誤差變量最大似然估計(jì)。吉布斯采樣作為一種典型的統(tǒng)計(jì)采樣算法,基于馬爾可夫鏈MC(Markov chain MC,MCMC)[16]方法建立,能夠在確定后驗(yàn)概率分布的條件下,通過(guò)迭代循環(huán)采樣來(lái)獲取參數(shù)樣本,進(jìn)而得到變量估計(jì)值。然而,對(duì)于高維數(shù)據(jù),吉布斯采樣算法運(yùn)算量高,運(yùn)行效率低。因此,本文運(yùn)用計(jì)算思路清晰、計(jì)算效率高的VB-EM算法實(shí)現(xiàn)對(duì)后驗(yàn)概率密度函數(shù)的求解。

本文中將Y,X,α,λ和β作為隨機(jī)變量,其中Y是顯變量,接收雷達(dá)目標(biāo)探測(cè)數(shù)據(jù)可以直接獲得,其他變量是隱變量,包含在Θ={X,α,λ,β}這個(gè)待求解隨機(jī)變量組成的集合中,這些隱變量的后驗(yàn)概率密度函數(shù)可以通過(guò)VB-EM算法求得。乘性干擾E被視為一個(gè)待估計(jì)的參數(shù),則式(3)的對(duì)數(shù)似然函數(shù)可以寫成[17]

lnp(Y;E)=F(q,E)+KL(q‖p)

(10)

式中，

(11)

(12)

式中，q(Θ)是近似的后驗(yàn)概率密度函數(shù);KL(q‖p)表示后驗(yàn)p(Θ|Y;E)和近似q(Θ)之間的Kullback-Leibler(KL)散度[18]。由于KL(q‖p)≥0,所以lnp(Y;E)≥F(q,E),也就是說(shuō),F(q,E)為對(duì)數(shù)似然函數(shù)的證據(jù)下界(evidence lower bound,ELOB),當(dāng)且僅當(dāng)p(Θ|Y;E)=q(Θ)時(shí),KL(q‖p)=0,此時(shí)q(Θ)可解,將其代入式(11)即可求得E。EM算法即是讓下界F(q,E)相對(duì)于q和E最大化。

在VB-EM算法中,根據(jù)平均場(chǎng)假設(shè)[15],可利用因式分解來(lái)近似q(Θ)，表示為

q(Θ)≈q(X)q(α)q(λ)q(β)

(13)

式中，q(·)表示對(duì)應(yīng)隨機(jī)變量的后驗(yàn)概率密度函數(shù)。基于式(13)中的因式分解,VB-EM算法采用兩步迭代過(guò)程,使變分E步中的下界F(q,E)和變分M步中的對(duì)數(shù)似然最大化。

將式(13)代入到式(11),可得相應(yīng)隨機(jī)變量Θi的解為

(14)

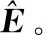
(15)

將式(3)、式(4)代入式(15)中可得

(16)

其中

(17)

式中，上標(biāo)H是共軛轉(zhuǎn)置算子,由式(16)可見(jiàn),待評(píng)估性能指標(biāo)X的后驗(yàn)概率密度函數(shù)估計(jì)服從復(fù)高斯分布;期望μ:m表示X第m個(gè)距離單元的均值,是對(duì)相應(yīng)雷達(dá)性能指標(biāo)的估計(jì),與線性最小均方誤差(linear minimum mean square error, LMMSE)估計(jì)[19]是一致的;Σm表示X的第m個(gè)距離單元的協(xié)方差矩陣,表示估計(jì)值的波動(dòng)范圍,可在此基礎(chǔ)上根據(jù)模型及需求確定待評(píng)估性能指標(biāo)的置信區(qū)間和置信度。

同理,根據(jù)式(14)可得超參數(shù)α的后驗(yàn)概率密度函數(shù)估計(jì),并將式(4)、式(5)代入可得αn m的第l階矩為

(18)

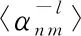
根據(jù)式(14)可得超參數(shù)λ的后驗(yàn)概率密度函數(shù)估計(jì),并將式(5)、式(6)代入,可得λm的每個(gè)元素服從Gamma分布,λm的均值為

(19)

同理,根據(jù)式(14)可得超參數(shù)β的后驗(yàn)概率密度函數(shù)估計(jì),并將式(3)、式(7)代入式(14),可得βm的每個(gè)元素服從Gamma分布,βm的均值為

(20)

式中，‖·‖F(xiàn)表示矩陣的Frobenius范數(shù);Tr(·)表示對(duì)矩陣求跡算子。在前面提出的變分近似貝葉斯推理中,通過(guò)迭代更新—直到收斂,可以得到雷達(dá)探測(cè)系統(tǒng)待評(píng)估性能指標(biāo)X。由于Θ中的隨機(jī)變量相互依賴,迭代過(guò)程可以極大程度地減小誤差,從而提高相應(yīng)指標(biāo)評(píng)估精度。另外,由于對(duì)加性觀測(cè)誤差精度β進(jìn)行了迭代更新,進(jìn)一步抑制了殘余雜波和去噪。由于在迭代過(guò)程中,各變量之間相互制約,隨著迭代次數(shù)的增加,隨機(jī)變量的均值逐漸收斂到期望值。

在變分最大化步驟,獲得隨機(jī)變量Θ的后驗(yàn)概率密度函數(shù)估計(jì)后,可通過(guò)下式對(duì)乘性誤差E的估計(jì)[14]進(jìn)行計(jì)算：

(21)

觀察式(21)可見(jiàn),目標(biāo)函數(shù)為非凸函數(shù),不存在閉合解,因此以坐標(biāo)下降方式來(lái)解決這個(gè)問(wèn)題,通過(guò)分別對(duì)E對(duì)角線上元素的實(shí)部和虛部計(jì)算偏導(dǎo)并置零可得乘性誤差的解為

(22)

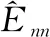
4 雷達(dá)性能指標(biāo)評(píng)估

本節(jié)基于上述基于貝葉斯機(jī)器學(xué)習(xí)得到的待評(píng)估指標(biāo)X和超參數(shù)α,λ,β的后驗(yàn)概率密度函數(shù)估計(jì),實(shí)現(xiàn)對(duì)待評(píng)估指標(biāo)的動(dòng)態(tài)指示,提供相比傳統(tǒng)指標(biāo)評(píng)估方法所不能提供的數(shù)學(xué)解析動(dòng)態(tài)變化范圍。系統(tǒng)評(píng)估過(guò)程必然存在可信度[20-23]的問(wèn)題,缺乏足夠可信度的評(píng)估系統(tǒng)是沒(méi)有應(yīng)用價(jià)值的,其評(píng)估結(jié)果甚至?xí)?duì)戰(zhàn)略決策者造成誤導(dǎo),釀成無(wú)法挽回的后果,所以在對(duì)雷達(dá)探測(cè)系統(tǒng)進(jìn)行性能評(píng)估時(shí),有必要對(duì)雷達(dá)相應(yīng)性能指標(biāo)的置信度和置信區(qū)間進(jìn)行評(píng)估。

在統(tǒng)計(jì)學(xué)中,一個(gè)概率樣本或概率密度函數(shù)的置信區(qū)間,是對(duì)這個(gè)樣本的某個(gè)總體參數(shù)的區(qū)間估計(jì),置信區(qū)間展現(xiàn)的是這個(gè)總體參數(shù)的真實(shí)值有一定概率落在與該測(cè)量結(jié)果有關(guān)的某對(duì)應(yīng)區(qū)間,置信區(qū)間給出了生成總體參數(shù)的真實(shí)值在測(cè)量值的區(qū)間所具有的可信程度,即前面所要求的“一定概率”,這個(gè)概率被稱為置信水平,即為置信度。

置信區(qū)間給出了相應(yīng)估計(jì)值以一定的置信水平屬于該區(qū)間的可靠性,不僅僅給出了動(dòng)態(tài)的變化范圍,而且給出了在該區(qū)間內(nèi)變化的可信度。更重要的是,由于可以解析計(jì)算出相應(yīng)指標(biāo)變量的后驗(yàn)概率密度函數(shù),因此可以直接解析計(jì)算相應(yīng)的估計(jì)值即期望以及動(dòng)態(tài)變化范圍即置信區(qū)間,并不需要對(duì)系統(tǒng)進(jìn)行多次重復(fù)性實(shí)驗(yàn),以獲取大量檢驗(yàn)樣本,從而大大降低了系統(tǒng)測(cè)試及檢驗(yàn)的復(fù)雜度,降低系統(tǒng)測(cè)試運(yùn)行成本,提供更加清晰、可靠、豐富的指標(biāo)指示。例如,如果求解獲得的某一指標(biāo)變量的后驗(yàn)概率密度為高斯分布,如：

p(X|Y)=CN(X;μ,Σ)

(23)

式中，μ表示期望;Σ表示協(xié)方差矩陣,由期望和協(xié)方差矩陣可構(gòu)建式(23)所示高斯分布的置信區(qū)間。簡(jiǎn)單分布的置信區(qū)間容易計(jì)算,如果某一誤差變量服從均值為0、方差為1的標(biāo)準(zhǔn)正態(tài)分布,其置信區(qū)間通常表示為在區(qū)間[-3,3]的概率為99.73%。也就是說(shuō),誤差在±3區(qū)間內(nèi)的概率是99.73%。針對(duì)更加復(fù)雜形式的概率分布置信區(qū)間計(jì)算則可通過(guò)如下計(jì)算公式計(jì)算：

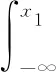
(24)

式(24)表示了變量X在后驗(yàn)概率密度函數(shù)p(X|Y)下的置信區(qū)間[x0,x1]內(nèi)的置信度為P。利用式(24)可對(duì)任意形式的后驗(yàn)概率密度函數(shù)求解其置信區(qū)間及置信度。而對(duì)于常用形式的后驗(yàn)概率密度函數(shù),則可以通過(guò)其提供的一階距(即均值)及二階矩(即方差)進(jìn)行計(jì)算。

本文以典型雷達(dá)目標(biāo)探測(cè)為例,對(duì)測(cè)高精度和檢測(cè)概率進(jìn)行動(dòng)態(tài)評(píng)估。對(duì)于測(cè)高結(jié)果的估計(jì)值均值和方差即為式解析計(jì)算的結(jié)果,通過(guò)均值和方差可以完成對(duì)測(cè)高精度的動(dòng)態(tài)評(píng)估。對(duì)于檢測(cè)概率,其表達(dá)式為

(25)

5 實(shí)驗(yàn)驗(yàn)證

本文所提方法無(wú)需多次獨(dú)立同分布實(shí)驗(yàn),僅需單次測(cè)量結(jié)果,便可以獲得動(dòng)態(tài)變化區(qū)間,通過(guò)建立模型代替實(shí)驗(yàn),也就是說(shuō)在不同的環(huán)境下,當(dāng)目標(biāo)滿足稀疏性時(shí),根據(jù)已建立好的概率模型即可推導(dǎo)相應(yīng)的指標(biāo)估計(jì)值及相應(yīng)的動(dòng)態(tài)范圍,有很好的指示效果,大大降低了系統(tǒng)開(kāi)發(fā)、測(cè)試及檢驗(yàn)成本。為了驗(yàn)證所提的非監(jiān)督貝葉斯學(xué)習(xí)雷達(dá)性能動(dòng)態(tài)評(píng)估方法的有效性和通用性,本節(jié)以測(cè)高精度和檢測(cè)概率兩個(gè)雷達(dá)性能指標(biāo)為例,將本文所提方法與傳統(tǒng)MC方法做對(duì)比,并引入處理增益來(lái)直觀地顯示兩種方法的比較結(jié)果,最后改變仿真的環(huán)境,驗(yàn)證本文方法在不同分布的干擾情況下的通用性。

5.1 測(cè)高精度

5.1.1 不同SNR下的測(cè)高精度

本節(jié)以測(cè)高精度為例,通過(guò)將本文方法與傳統(tǒng)MC方法做對(duì)比來(lái)驗(yàn)證本文方法在雷達(dá)性能動(dòng)態(tài)評(píng)估中的穩(wěn)健性和有效性。目標(biāo)仿真參數(shù)如下:信號(hào)帶寬為1.5 GHz,脈沖重復(fù)頻率為1 000 Hz,載波頻率為10 GHz,方位向采樣脈沖數(shù)為1 156,目標(biāo)個(gè)數(shù)為3,其相對(duì)于背景呈稀疏性,目標(biāo)分別在(245,579,863)的位置,對(duì)應(yīng)的高度分別為(80 m,100 m,60 m),目標(biāo)高度評(píng)估對(duì)應(yīng)的置信區(qū)間為[μ-3σ,μ+3σ],置信度為99.73%。

圖1表示不同SNR下本文方法與傳統(tǒng)MC方法測(cè)高精度的對(duì)比,其中左側(cè)表示用傳統(tǒng)方法測(cè)得的結(jié)果,右側(cè)表示本文方法測(cè)得的結(jié)果,陰影圓柱表示檢測(cè)目標(biāo)真實(shí)高度值,分別是80 m、100 m和60 m,實(shí)心圓點(diǎn)表示相應(yīng)方法估計(jì)的均值,垂直誤差條表示相應(yīng)方法得到的方差,仿真中設(shè)置了3種加噪聲場(chǎng)景,SNR分別為0 dB、10 dB和20 dB。

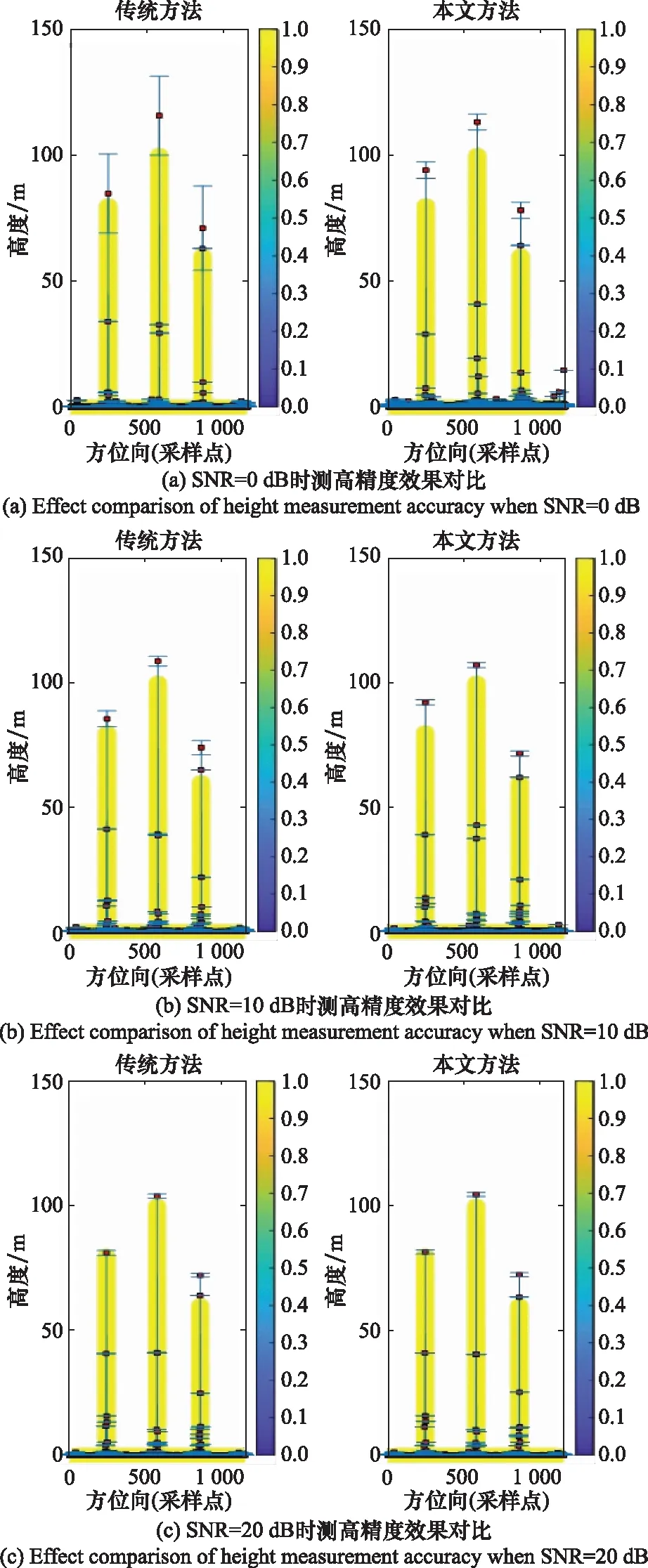
圖1 不同SNR情況下測(cè)高精度效果對(duì)比

從圖1中可看出,本文方法與傳統(tǒng)MC方法在相同的環(huán)境下對(duì)高度評(píng)估的估計(jì)值以及其對(duì)應(yīng)的置信區(qū)間和置信度。低SNR時(shí)如圖1(a)所示,本文方法比傳統(tǒng)MC方法得到的方差小,波動(dòng)范圍小,即得到的置信區(qū)間窄,估計(jì)結(jié)果更準(zhǔn)確,可信度更高,性能評(píng)估結(jié)果更好,這是由于本文方法對(duì)觀測(cè)誤差精度β進(jìn)行了概率統(tǒng)計(jì)建模。中等SNR時(shí)如圖1(b)所示,兩種方法得到的置信區(qū)間相比于低SNR時(shí)都有所變窄,但本文所提方法得到的置信區(qū)間更窄,評(píng)估性能更好。高SNR時(shí)如圖1(c)所示,兩種方法性能評(píng)估結(jié)果基本一致。通過(guò)比較3種同SNR情況下的測(cè)高精度結(jié)果,不難發(fā)現(xiàn),當(dāng)置信度一定時(shí),隨著加入噪聲的減小,本文方法和傳統(tǒng)MC方法得到的估計(jì)值越接近目標(biāo)真實(shí)高度值,估計(jì)產(chǎn)生的方差也越小,估計(jì)越精確,兩種方法的趨勢(shì)一致,驗(yàn)證了本文方法的穩(wěn)健性和有效性。

5.1.2 測(cè)高精度處理增益

為了更加直觀地衡量本文方法的優(yōu)越性,本節(jié)實(shí)驗(yàn)引入測(cè)高精度處理增益來(lái)驗(yàn)證,將傳統(tǒng)MC方法得到的方差與本文所提方法得到的方差之比定義為測(cè)高精度的處理增益,即

(26)

式中，GH表示測(cè)高精度的處理增益;σMC表示通過(guò)傳統(tǒng)MC方法得到的高度估計(jì)值均方差;σ表示用本文方法得到的高度估計(jì)值均方差。

測(cè)高精度處理增益結(jié)果如圖2所示,圖中橫坐標(biāo)表示SNR,縱坐標(biāo)表示測(cè)高精度的處理增益值,“*”表示測(cè)高精度處理增益的具體值,曲線是對(duì)該具體值的擬合,其中直線增益值為1以更直觀的觀察。圖2中測(cè)高精度的處理增益值恒大于1,說(shuō)明利用本文所提方法得到的高度方差總是比利用MC方法得到的高度方差小,精確度高,這種優(yōu)勢(shì)在低SNR的情況下更明顯,驗(yàn)證了所提方法的優(yōu)越性。

圖2 測(cè)高精度處理增益

5.1.3 非高斯分布干擾的測(cè)高精度

本節(jié)實(shí)驗(yàn)在非高斯分布干擾的情況下用本文方法實(shí)現(xiàn)對(duì)雷達(dá)系統(tǒng)測(cè)高精度的評(píng)估,并與干擾服從高斯分布時(shí)的評(píng)估結(jié)果做對(duì)比來(lái)驗(yàn)證本文方法的通用性。仿真結(jié)果如圖3所示,左側(cè)表示干擾服從高斯分布時(shí)的評(píng)估結(jié)果,右側(cè)表示干擾服從非高斯分布時(shí)的評(píng)估結(jié)果,兩個(gè)分布干擾的SNR均為10 dB,置信度均為99.73%,柱狀陰影部分代表檢測(cè)目標(biāo)真實(shí)高度值,分別是80 m,100 m,60 m,實(shí)心圓點(diǎn)表示估計(jì)的均值,垂直誤差條表示相應(yīng)分布的干擾用本文方法得到的方差。不難發(fā)現(xiàn),無(wú)論干擾服從哪種分布,都能測(cè)出高度的估計(jì)值并確定置信區(qū)間,說(shuō)明本文方法可以對(duì)不同分布干擾下的高度進(jìn)行動(dòng)態(tài)評(píng)估,證明了本文方法的通用性。

圖3 SNR=10 dB時(shí)不同分布干擾下本文方法的測(cè)高精度

5.2 檢測(cè)概率

5.2.1 恒虛警率下的檢測(cè)概率

本節(jié)以檢測(cè)概率為例,在恒虛警率的條件下,改變不同的SNR,得到本文方法下的檢測(cè)概率以及該概率對(duì)應(yīng)的置信區(qū)間,并將其與傳統(tǒng)MC方法在相同環(huán)境下的仿真做比對(duì)來(lái)驗(yàn)證本文方法的高效性。仿真結(jié)果如圖4所示,取恒虛警率的值為10-4。

圖4 Pfa=10-4時(shí)檢測(cè)概率效果對(duì)比

首先,運(yùn)用本文方法,不僅可以得到檢測(cè)概率的估計(jì)值,還可以得到該估計(jì)值的上限和下限,即置信區(qū)間,以動(dòng)態(tài)的范圍及估計(jì)來(lái)完成對(duì)檢測(cè)概率的評(píng)估。其次,低SNR時(shí),相同環(huán)境下,本文方法比傳統(tǒng)MC方法得到的檢測(cè)概率高,即便是本文方法所得檢測(cè)概率的下限,性能評(píng)估結(jié)果也比傳統(tǒng)MC方法好,充分說(shuō)明了本文方法的高效性;另外,在SNR=-2 dB時(shí),有一個(gè)突變,這是由于估計(jì)值噪聲方差大,傳統(tǒng)MC方法估計(jì)的噪聲方差要比動(dòng)態(tài)評(píng)估估計(jì)的噪聲方差大,根據(jù)Cramér-Rao界(Cramér-Rao bound,CRB)可知估計(jì)值方差是有下限的,說(shuō)明本文方法得到的方差更接近CRB,效果要比傳統(tǒng)的MC方法好,充分體現(xiàn)了本文方法的穩(wěn)健性。最后,通過(guò)圖4可發(fā)現(xiàn),當(dāng)虛警率一定時(shí),兩種方法得到的檢測(cè)概率隨著SNR的增大而變高,證明了本文方法的有效性。

5.2.2 檢測(cè)概率處理增益

為了直觀地衡量本文方法的高效性,本節(jié)實(shí)驗(yàn)引入檢測(cè)概率處理增益來(lái)驗(yàn)證,將本文方法優(yōu)于MC方法部分與本文方法劣于MC方法部分的比值定義為恒虛警率的處理增益。如圖5所示,以傳統(tǒng)MC方法在不同SNR下得到的檢測(cè)概率為界,將本文方法得到的檢測(cè)概率分成左右兩部分,陰影部分由本文方法在不同SNR下得到的檢測(cè)概率估計(jì)值的上限和下限組成,左側(cè)深色陰影部分為同SNR下本文方法對(duì)檢測(cè)概率的評(píng)估優(yōu)于傳統(tǒng)MC方法對(duì)檢測(cè)概率評(píng)估的部分,右側(cè)淺色陰影為本文方法對(duì)檢測(cè)概率的評(píng)估劣于傳統(tǒng)MC方法對(duì)檢測(cè)概率評(píng)估的部分,檢測(cè)概率的處理增益GPd定義為

(27)

圖5 檢測(cè)概率處理增益示意圖

檢測(cè)概率處理增益結(jié)果如圖6所示,“o”表示具體的檢測(cè)概率增益值,實(shí)曲線是對(duì)具體值的擬合,圖中直線的檢測(cè)概率處理增益值為1。不難發(fā)現(xiàn),無(wú)論恒虛警率取多少,檢測(cè)概率的處理增益值恒大于1,說(shuō)明在同樣的條件下,本文方法得到的檢測(cè)概率比傳統(tǒng)MC方法得到的檢測(cè)概率高,特別是在低虛警率低SNR的情況下,效果更明顯,充分體現(xiàn)了本文方法的高效性。

圖6 檢測(cè)概率處理增益

5.2.3 非高斯分布干擾的檢測(cè)概率

本節(jié)實(shí)驗(yàn)研究不同分布干擾環(huán)境下改變SNR的檢測(cè)概率,并與傳統(tǒng)MC方法做比對(duì)來(lái)驗(yàn)證本文方法的通用性。仿真結(jié)果如圖7所示。從圖7中可以看出,當(dāng)干擾服從非高斯分布時(shí),隨著SNR的變化,得到的結(jié)果與干擾服從高斯分布時(shí)用本文方法得到的結(jié)果以及用傳統(tǒng)MC方法的結(jié)果的趨勢(shì)是一致的,證明了本文方法通用性;雖然干擾服從非高斯分布時(shí)用本文方法得到的檢測(cè)概率結(jié)果比干擾服從高斯分布時(shí)本文方法得到的檢測(cè)概率結(jié)果低,但是比同情況下的用傳統(tǒng)MC方法得到的檢測(cè)概率高,這充分證明了本文方法的高效性。

圖7 Pfa=10-4時(shí)不同分布干擾的檢測(cè)概率對(duì)比

6 結(jié) 論

本文針對(duì)雷達(dá)系統(tǒng)性能指標(biāo)的評(píng)估,運(yùn)用復(fù)雜變化的雷達(dá)目標(biāo)特性和環(huán)境變量進(jìn)行了概率與統(tǒng)計(jì)建模,并基于貝葉斯機(jī)器學(xué)習(xí)理論獲取了解析的雷達(dá)性能指標(biāo)后驗(yàn)概率密度函數(shù),從而實(shí)現(xiàn)了對(duì)性能指標(biāo)動(dòng)態(tài)變化的定量評(píng)估。實(shí)驗(yàn)應(yīng)用多組數(shù)據(jù)多種環(huán)境進(jìn)行驗(yàn)證,同時(shí)對(duì)比傳統(tǒng)MC評(píng)估方法,證明了本文所提動(dòng)態(tài)評(píng)估方法的有效性和優(yōu)越性。然而,在實(shí)驗(yàn)過(guò)程中,本文方法對(duì)小范圍動(dòng)態(tài)變化實(shí)測(cè)數(shù)據(jù)的評(píng)估指示有限,有必要研究適用于更多應(yīng)用場(chǎng)景的評(píng)估方法,這將是后續(xù)工作的重點(diǎn)。