超大型干線集裝箱船配載優化

成保辰, 郭蘊華, 張青雷, 牟軍敏, 胡 義

(1.武漢理工大學 a.船舶動力工程技術交通行業重點實驗室；b.能源與動力工程學院；c.航運學院， 武漢 430063;2.上海海事大學 中國(上海)自貿區供應鏈研究院， 上海 201306)

集裝箱自引入到海上運輸貿易中以來，因其具有高效率、低成本等優點而掀起了一場全球航運業的革命。根據聯合國貿易和發展會議(United Nations Conference on Trade and Development，UNCTAD)[1]發布的《2018年海運報告》,2018年全球集裝箱貿易總量達到約1.48億TEU，年增幅達6.4%，創下了自2011年以來的最大增幅。UNCTAD預測2018—2023年海運集裝箱貿易將以每年約6.0%的速度增長，增幅遠超其他海運方式。

隨著集裝箱船智能化和大型化的不斷推進，單箱位運營成本大幅下降。因此各大航運公司紛紛訂造超大型集裝箱船(Ultra-Large Container Ship,ULCS),并引入相關智能管理系統。DYNALINERS[2]的分析數據顯示:2018年全球已有451艘ULCS投入運營，另外尚有129艘處于建造狀態。ULCS已成為國際干線航線上運營的主要船型。[3]

智能配載是智能船舶系統的重要組成部分，其中集裝箱船多港口Bay位優化問題,指已知各港口裝載需求數據求解船舶在全航線上的配載方案。該問題已被證明為復雜的NP-hard優化問題。[4]優秀的配載方案應滿足船舶航行中強度、浮態、靠港時間和裝載率等要求,以保證船舶安全、高效地運營。[5]PACINO等[6]提出考慮壓載水的線性模型，用于生成港口的積載計劃，采用一種線性化船舶重心計算和靜水數據表的方法處理排水量可變情況下的穩性和應力力矩約束;AMBROSINO等[7-11]沿襲WILSON等[12]提出的從戰略和戰術2個層面解決多港口配載問題的路線，提出解決戰略層面配載問題的多港口Bay位優化混合整數規劃(Mixed Integer Programming,MIP)模型。該模型考慮到集裝箱船的艙口和不規則龍骨，可處理標準集裝箱和冷藏箱的配載問題;ZHANG等[13]針對船舶在不同港口移箱費用不同的特點,提出MIP模型，使全航線中靠港總移箱費用最低，并采用改進的遺傳算法進行求解。

在已有研究中，并沒有將ULCS的強度和精確穩性作為優化約束條件，但該約束對于保障遠洋航線ULCS的安全性而言至關重要。本文以文獻[9]、文獻[10]和文獻[14]中的模型為基礎做出改進，針對干線集裝箱船航程長、裝載量大和對船舶強度要求高等特點，同時為避免以貨艙為基本單元的模型在求解層數多、裝載量大的ULCS時易出現裝載率較低等問題，提出以堆垛和貨艙為基本單元，兼顧堆垛內倒箱和開艙蓋倒箱2種情況，考慮船體精確強度約束并對穩性約束做出改進的模型。該模型同時滿足提高裝載率和保障近海、遠海航行安全的要求。

1 問題描述

ULCS結構示意見圖1，已知其結構信息和整條航線上每個港口待裝卸集裝箱的種類、尺寸和數量以及出發港、目的港等信息，據此制訂出整條航線上各港口的戰略配載方案。該方案需滿足所有集裝箱的裝載和船舶適航性的要求，同時須使靠港時間最短。

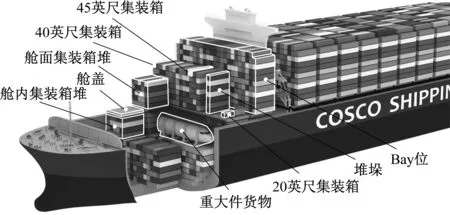
圖1 ULCS結構示意

集裝箱倒箱是在卸載集裝箱時，因先到港箱在后到港箱的下方，故在對其進行卸載時,需先卸載上方的后到港箱,該操作會增加運營成本,應設法消除倒箱。本模型中倒箱可分為同堆垛內倒箱和因開艙蓋操作導致的艙蓋上倒箱。倒箱數分別為該堆垛內先到港箱上方所有后到港箱數和本貨艙艙蓋上所有后到港箱數。

船舶在港口的裝卸時間取決于速度最慢的岸吊完成作業的時間，故所有岸吊作業量應平均分配，使其同時完成裝載作業，提升岸吊利用效率。本文以倒箱數最少和岸吊操作次數之差最少為目標縮短靠港時間。

2 多港口配載問題的數學模型

2.1 數據預處理

根據航線中重大件貨物的尺寸,將其長lb、寬wb和高hb除以40英尺集裝箱的長lt、寬wt和高ht,并向上取整得到該貨物占用40英尺集裝箱位的數量HLno，將2HLno設為重大件貨的折算TEU數。據此,在相應航段中船舶Bay位艙蓋下的貨艙內預留出該貨物的空間。為防止甲板上堆垛中出現單數個20英尺箱的情況，對相同目的港的2個20英尺箱同時編組進行計算。

為降低船舶航行時的重心，提高船舶的安全性，該模型假設船舶在離港時船底壓載艙為滿載狀態。在確定各港裝載信息之后，根據排水量計算式求得p港離港時的排水量Dispp為

(1)

式(1)中Wi,p為船舶在p港第i部分的重量;W空船為空船重量;C為船舶常數。根據Dispp在靜水力曲線表中二次插值可得到在p港離港時,船舶正浮狀態下的浮心縱向坐標LCBp和每厘米縱傾力矩MCTp。

船舶離港時空船、油水和備品部分的重量與重心位置已確定，故船舶總重心只與集裝箱的布置有關。為減少后續求解重心時的計算量，可根據式(2)求得離港前船舶縱向和橫向的固定力矩Mbacedim為

(2)

式(2)中:當dim=lo和ho時,Cogi,dim分別為i部分的LCG和TCG。

根據文獻[6]中由邦金曲線求解站間浮力的公式求得p港每站間的浮力,記作Dp,sta。

(3)

式(3)中：δw為海水的密度;Δl為站間距;kiWs+bi為對船舶邦金曲線的分段線性擬合。

2.2 模型數據集

P為全航線中所有港口的集合；D為所有港口間航線的集合；Dp為途經p港或p港為始發港的航線集合；Dp-為途經p港，但p港不為始發港的航線集合；H和ST分別為表示船舶貨艙和堆垛的集合；BAY為船舶Bay位的集合；G為集裝箱重量類別的集合(g=0為空箱、g=1為輕箱、g=2為中等箱、g=3為重箱)；S為集裝箱尺寸類別的集合(s=1為20英尺集裝箱(占1 TEU箱位);s=2為40英尺集裝箱(占2 TEU箱位);s=3表示45英尺集裝箱(本模型中占2 TEU箱位))；T為貨物種類類別的集合(t=1為普通箱;t=2為冷藏箱;t=3為重大件貨物)；Cogh,dim為貨艙h的橫縱坐標集合(dim=lo為縱向;dim=ho為橫向)；Yp為p港岸吊的集合；Hpc為p港岸吊c負責的貨艙的集合；HBay為船舶Bay位包含的貨艙集合；Kh為貨艙h中包含的堆垛的集合；Sta為船舶分站的集合；Ksta和Hsta分別為船舶sta站所包含的堆垛和貨艙的集合；Dispp為各港口離港時船舶排水量的集合；Dp,sta船舶在p港離港時，各站浮力的集合；Nstation,max和Mstation,max分別為船體各強度控制點剪力和彎矩最大許用值的集合；STAm為彎矩控制點所在站號的集合；perpn和perpm分別為船舶在p港到p+1港間，船體剪力和彎矩的安全閾值所占船體強度最大許用值百分比參數的集合。

2.3 模型參數

np為航線上港口總數；Chh和Chht分別為貨艙h艙蓋下的貨艙可容納的TEU箱總數和t種類集裝箱的TEU箱數；Ckk和Ckkt分別為甲板上堆垛k中可容納的TEU箱總數和t類集裝箱的TEU箱數；Qhobal為在近似無橫傾角狀態時,左、右舷各部分重量對船體中心線的橫向矩的最大差值；Nmix為同一堆垛內可存在的不同目的港的數量；Nod,stg為尺寸為s、種類為t、重量等級為g、始發港為o、目的港為d的自然箱數；Wg為重量等級為g的集裝箱重量(對于20英尺集裝箱,W0=2.5 t,W1=7 t,W2=14 t,W3=21 t；對于40英尺集裝箱,W0=4 t,W1=10 t,W2=20 t,W3=30 t；對于45英尺集裝箱,W0=5 t,W1=12 t,W2=24 t,W3=36 t)；TRIMmax為船舶離港時最大縱傾限制；opt,s為尺寸s種類t的集裝箱每TEU岸吊操作次數，本模型采用雙起升機構40英尺集裝箱岸橋，可同時吊起2個40英尺集裝箱或4個20英尺集裝箱，故20英尺集裝箱為1/4，40英尺集裝箱和45英尺箱為1/2，重大件貨物為1/HLno；PWf為各目標函數線性加權的權重(f=1,2)；Δl為船舶站間距。

2.4 模型變量

xhodh,stg和xdodk,stg為非負整數變量，表示在貨艙h或堆垛k中尺寸為s、種類為t、重量等級為g、出發港為o和目的港為d的自然箱數(xh和xd分別為艙蓋下和艙蓋上的貨艙)；yhpdh和ydpdk為布爾型變量，分別為若在p港、貨艙h中有目的港為d的集裝箱，則yhpdh=1，反之yhpdh=0；若在p港，艙蓋上的堆垛k中有目的港為d的集裝箱，則ydpdk=1，反之ydpdk=0；rph為非負整數變量，表示在p港、貨艙h中發生卸載艙蓋下的集裝箱和向艙蓋下裝載集裝箱中任意一個行為時，艙蓋上堆垛k的自然箱倒箱數；rpk為非負整數變量，表示在p港、堆垛k中，艙蓋上堆垛k的自然箱倒箱數；fph和fpk為布爾型變量，分別表示在p港，若貨艙h中艙蓋下存在集裝箱的裝載或卸載作業，需要艙蓋上的貨艙h中的集裝箱進行倒箱，則fph=1，反之fph=0；若堆垛k中存在堆垛內倒箱,則fpk=1，反之fpk=0；Xpk為正整數變量，表示船舶在p港時、堆垛k中,集裝箱最遠的目的港的編號；Lp,sta為實數變量，表示船舶離開p港時，sta站的載荷；Np,station為實數變量，表示船舶離開p港時，station與station+1站間的剪力；LCGp為實數變量，表示船舶離開p港時的縱向重心與艉垂線的距離；Mp,station為實數變量，指船舶各彎矩控制點的彎矩；oppc為非負實數松弛變量，表示在p港，岸吊c的操作次數；Δpce為非負實數松弛變量，表示在p港，任意2臺岸吊c和e的操作次數差值的絕對值；Δmax為非負實數松弛變量,表示Δpce的最大值。

2.5 數學規劃模型

2.5.1目標函數

(4)

式(4)為該模型的目標函數，通過將倒箱數最少和最大吊機操作次數之差最小的多目標函數,通過線性加權法轉化為單目標函數，各目標函數的權重分別為PW1和PW2。

2.5.2約束函數

s∈S;t∈T;g∈G

(5)

式(5)為所有貨艙和堆垛中各類集裝箱自然箱數之和必須等于整條航線上的貨運總量。

p∈P;p≠1;p≠pmax;h∈H

(6)

式(6)為在p港，若貨艙h艙蓋下有目的港為d的集裝箱，且在p-1港，貨艙h艙蓋上的貨艙中有目的地為d的集裝箱，變量fph大于0，因其為布爾型變量，有fph=1。

(7)

(8)

式(7)和式(8)為在p港，每個貨艙h內集裝箱的目的港必須相同；同時,為提高集裝箱配載靈活性，使堆垛k內可裝載不同目的港的集裝箱，同一堆垛內集裝箱目的港個數不超過Nmix個。

2xhodh,45tg)≤Chhyhpdh,

p∈P;d∈P;d≠p;h∈H

(9)

2xdodk,45tg)≤Ckk×ydpdk,

p∈P;d∈P;d≠p;k∈ST

(10)

式(9)和式(10)為在p港，每個貨艙h(堆垛k)中的TEU數量不超過其容量限制。

2xhodh,45tg)≤Chht×yhpdh,

p∈P;d∈P;d≠p;t∈T;t>1;h∈H

(11)

2xdodk,45tg)≤Ckkt×ydpdk,

p∈P;d∈P;d≠p;t∈T;t>1;k∈ST

(12)

式(11)和式(12)為在p港，貨艙h(堆垛k)中種類為t的TEU箱數不能超過t類箱容量限制。

(o,d)∈D;k∈ST

(13)

式(13)為若堆垛k中存在45英尺集裝箱，則該堆垛中至少保留2個40英尺集裝箱，以滿足45英尺集裝箱的裝配要求。

p∈P;p>1;d∈P;d≠p;d≠p-1;h∈H

(14)

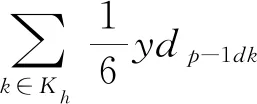
p∈P;h∈H

(15)

式(15)為計算p港因開艙蓋導致的倒箱數。

Xpk≥ydpdk×d,p∈P;k∈ST;(p,d)∈Dp

(16)

式(16)為在港口p，將堆垛k中集裝箱最遠的目的港的值d賦給Xpk，若堆垛k中無集裝箱，則將Xpk置0。

(Xpk-Xp-1k)/np-fph≤fpk,p∈P;h∈H;k∈Kh

(17)

式(17)為在港口p，若堆垛k中無集裝箱卸載操作且該堆垛所在貨艙不存在開艙蓋操作，同時堆垛內最遠集裝箱目的港Xpk變大，則表明堆垛k中有堆垛內倒箱情況，將變量fpk置1。

k∈ST;(o,d)∈D;d=Xpk

(18)

式(18)為計算p港堆垛k的堆垛內倒箱數。

p∈P

(19)

式(19)為計算p港船舶離港時船舶的LCGp。

|Dispp×(LCGp-LCBp)/(100MTCp)|≤TRIMmax,

p∈P

(20)

式(20)為在p港船舶離港時，船舶縱傾絕對值應不大于TRIMmax，以保證船舶為近似平吃水狀態。根據邦金曲線可計算得到當船舶縱傾絕對值不大于1 m時，船舶各站排水量與其平吃水狀態的相對誤差小于1%，由此可假設船舶為平吃水狀態。

p∈P

(21)

式(21)為p港船舶離港時，船艙內外左右舷堆裝的集裝箱箱重對船舶中線面橫向力矩應小于約束Qhobal，以減小集裝箱載荷對船體的橫向扭矩，并保證船舶為近似無橫傾角狀態。

p∈P;c∈Yp

(22)

式(22)為計算p港各岸吊的操作次數oppc。

|oppc-oppe|≤Δpce,

p∈P;c∈Yp;e∈Yp;c≠e

(23)

式(23)中:Δpce為p港岸吊操作次數的差值。

Δmax≥Δpce,

p∈P;c∈Yp;e∈Yp;c≠e

(24)

式(24)為整條航線中，計算所有岸吊操作次數差值的最大值Δmax。

sta∈STA;p∈P

(25)

式(25)為在p港，船舶離港時，根據船舶每站所受的重力與浮力之差求出該站的載荷Lsta,p。

p∈P;station∈STA

(26)

式(26)為在p港，船舶離港時對每站的載荷Lp,sta求積分得出每站間的剪力Np,station。

p∈P;station∈STAm

(27)

式(27)為在p港，船舶離港時對每站間剪力Np,station求積分得出站間控制點的彎矩Mp,station。

Np,station≤perpn×Nstation,max,

p∈P;station∈STA

(28)

Mp,station≤perpm×Mstation,max

p∈P;station∈STAm

(29)

式(28)和式(29)分別為船舶在p港，離港時船舶各點剪力和彎矩不能超過該點對應的閾值。各點船體強度的閾值根據下一航段距離，通過參數perpn和perpm進行調整。

(o,d)∈D;s∈S;t∈T;g∈G;h∈H;k∈ST

(30)

yhpdh∈{0,1},ydpdk∈{0,1},fpk∈{0,1},

p∈P;h∈H;k∈ST

(31)

式(30)和式(31)為配載方案中不可松弛為實數的變量。

3 計算試驗結果

選取裝載量為21 014 TEU、40英尺冷藏箱位為1 000個、Bay位數為24個、每個Bay位有4個艙蓋的ULCS作為試驗船舶。該船Bay位布置和縱向強度約束見圖2，結構參數見表1。船舶在離港時為近似正浮狀態，即船舶縱傾為平吃水狀態且橫向無橫傾角，同時艙底壓載水艙為滿載。配載的集裝箱貨物設定為普通箱、冷藏箱和重大件貨物等3種類型，其中普通箱有20英尺集裝箱、40英尺集裝箱和45英尺集裝箱等3種規格，每種規格又劃分為4個重量等級。根據干線航線中ULCS長途貨物遠多于短途貨物的特點[2]，假定

(32)

據此隨機生成11個航線場景。港口數為6的場景3～7中各港口貨運量、不同尺寸種類集裝箱比例以及所占船舶艙容百分比數據的平均值見表2。第8號和第9號場景見圖3，反映港口數為7的航線情況。在整個環線中，集裝箱船靠港順序為

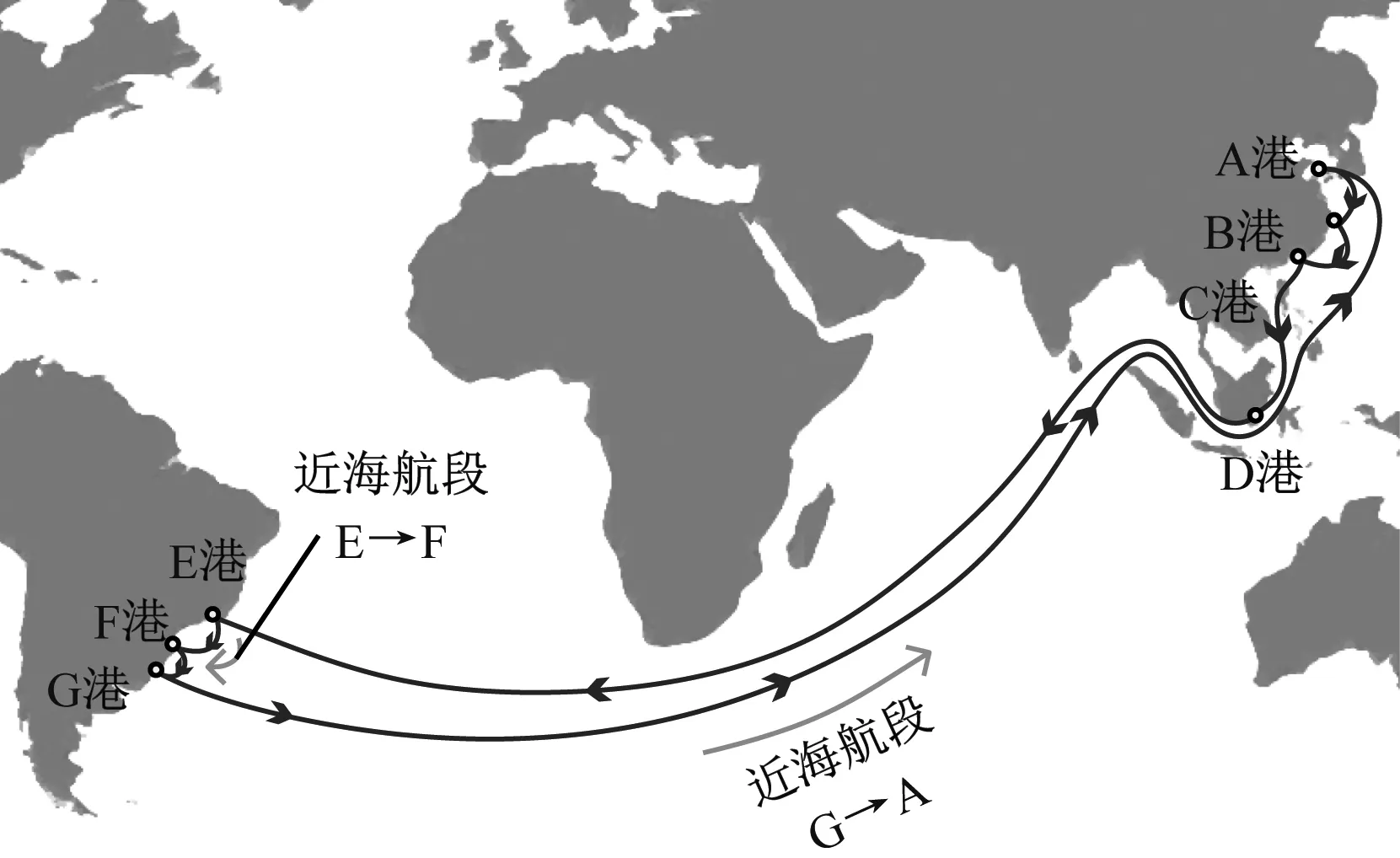
圖3 港口數為7的遠洋干線航線示意

圖2 ULCS的Bay位布置圖和縱向強度約束示意

表1 船舶結構參數

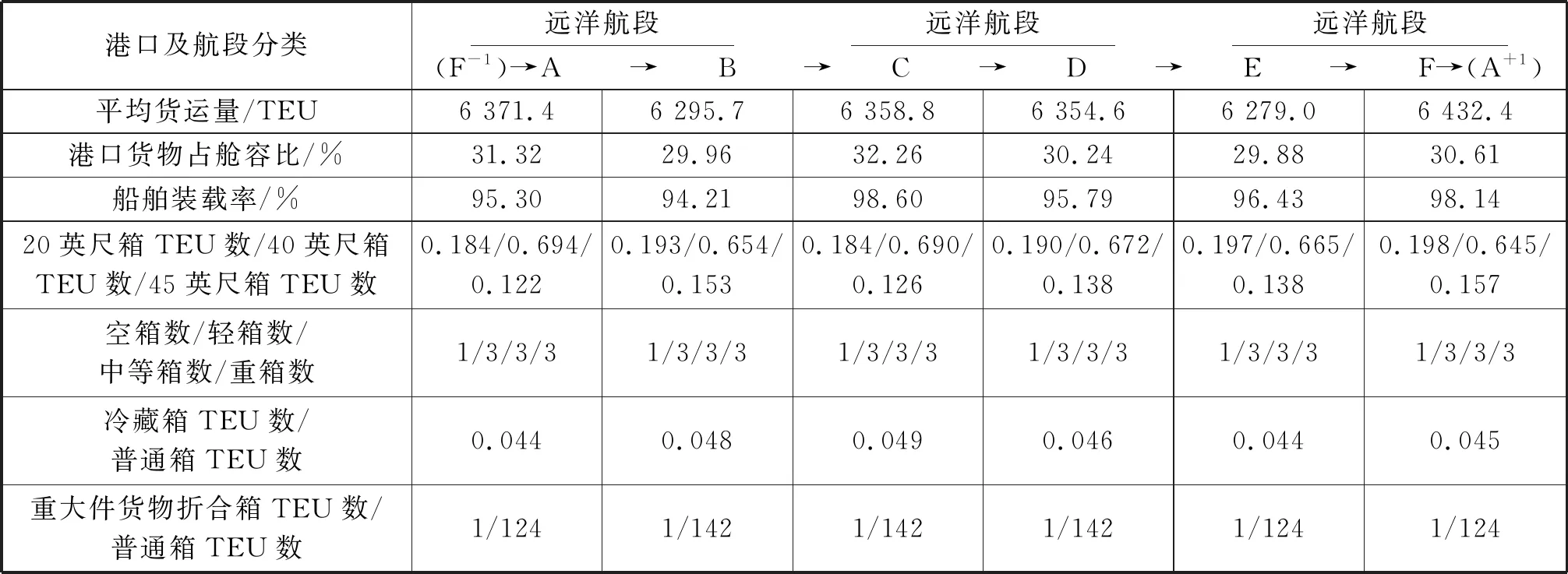
表2 場景3～場景7中各港口平均貨運數據

F-1→G-1→A→B→C→D→E→F→

G→A+1→B+1→…

(33)

式(33)中:F-1和G-1為上一輪循環中的F港和G港，A+1和B+1為下一輪循環中的A港和B港。將航行距離較遠的遠洋航段G-1→A、D→E和G→A+1的剪力和彎矩約束百分比perpn和perpm分別設置為90%和80%。為在保證船舶近海航行安全的同時提高求解速度，將近海航段站間剪力和彎矩約束百分比perpn和perpm放寬至95%和90%。各港口可用岸吊數量最大值為10。

模型中艙蓋以下的集裝箱以貨艙H而非堆垛ST為基本單元進行計算，同時艙蓋上堆垛內不同目的港數量Nmix值被設置為2，這些策略可在兼顧集裝箱配載靈活性的同時提高求解速度，也可有效減少開艙蓋操作次數。

將船舶相關參數約束和貨運量數據代入該模型，通過計算為增加可行解數量，將岸吊操作次數松弛為正實數。在其他變量不松弛的情況下，松弛的岸吊操作次數仍可作為配載方案優劣的評價標準。[10]該模型在雙2.5 GHz CPU、96線程、128 GRAM配置的服務器環境中，使用C++編程并調用CPLEX 12.9求解器求解，求解結果見表3。

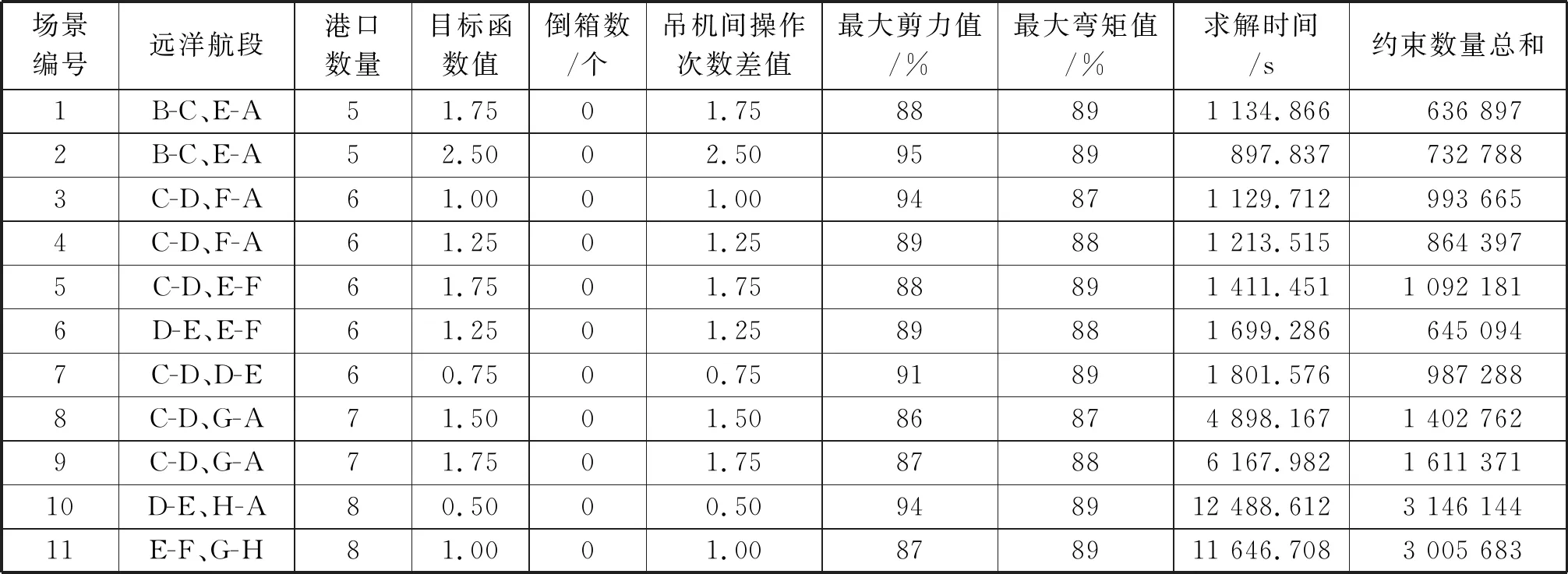
表3 不同場景中目標函數的計算結果

由表3可知:所有航線場景都能求解出倒箱數為0且岸吊操作次數差值小于3的配載方案。港口數分別等于5、6、7和8時,平均能在1 016 s、1 451 s、5 533 s和12 067 s內找到最優解。相對于干線船舶數天的航行時間來說，該時間是可接受的。

為驗證該模型對特種貨物配載的有效性，將重大件貨物和冷藏箱的裝載比例逐漸提高，計算結果見圖4和圖5。

重大件貨物裝載計算試驗結果如圖4所示。其試驗條件為:在港口數分別為5和6時，航線特征、出發—目的港貨運量、穩性和強度約束分別與場景1和場景3中各項約束相等。在保持不變的情況下，將重大件貨物的運量不斷提高。每個場景重復5次計算試驗，可得重大件貨物折算TEU數與求解時間的對應關系。該試驗結果表明:該模型的求解時間隨重大件貨物運量的增加而縮短，該特性源于數據預處理將特種箱位置固定的啟發式規則，縮小求解問題的空間，提高求解速度，驗證該模型可高效地解決不同裝載場景中重大件貨物的配載問題。

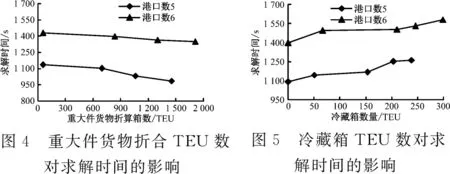
冷藏箱裝載計算試驗結果如圖5所示。該試驗在港口數分別為5和6的場景中，使航線特征、出發—目的港貨運量、穩性和強度約束分別與場景1和場景3中各項約束相等，并將其固定。逐漸增加各港口40英尺冷藏箱的裝卸數量，直至約束上限。重復5次計算試驗，可得模型求解時間與冷藏箱數量的對應關系。該試驗結果表明:隨著冷藏箱數量的增加，求解時間不斷增加。在港口數分別為5和6且全航線中冷藏箱滿載的情況下，最優解的求解時間，最大值為1 260 s和1 570 s均在可接受范圍內，驗證該模型能滿足不同冷藏箱裝載場景的求解需求。

上述各試驗結果表明:該配載模型可保證ULCS在近海和遠洋航行時的安全，可有效解決ULCS在不同場景中的配載問題。

4 結束語

本文通過對ULCS的結構和航線特點進行分析，提出該船型的多港口Bay位優化問題的模型。

1) 該模型以倒箱數最少，岸吊操作次數差值最小為目標，縮短船舶靠港時裝卸貨的時間。

2) 提出ULCS的精確剪力彎矩模型，并改進原有穩性模型，提高船舶在不同航區航行時的安全性。

3) 根據航段的距離，動態地調整船舶的結構強度約束，保證各航區的安全的同時,提高求解速度。

4) 提出重大件貨物的配載策略，同時,考慮冷藏箱和45英尺集裝箱的裝載需求，并驗證其有效性。

該模型也存在未考慮船舶垂向重心高度約束、未考慮危險品集裝箱和超限集裝箱貨物裝載約束等限制條件，仍需不斷完善。試驗結果表明:該創新多港口配載模型可在解決遠洋干線ULCS多港口Bay位優化問題時,有效提升ULCS配載效率，加快集裝箱船大數據智能運維平臺軟件國產化進程。