彈道解算用數值天氣預報風修正系數辨識

曹樹新,李 巖,李帥孝,徐樹威

(1.南京理工大學 能源與動力工程學院,江蘇 南京 210094;2.陸軍裝備部 沈陽地區軍事代表局駐沈陽地區第二軍事代表室,遼寧 沈陽 110004;3.齊齊哈爾建華機械有限公司,黑龍江 齊齊哈爾 161006)

隨著快速機動能力的不斷增強和偵察校射技術的不斷發展,現代戰爭對火炮的快速反應能力提出了更高要求,氣象保障作為火炮射擊保障的核心環節之一,有必要在提升氣象保障的速度和精度方面加以研究[1]。近年來,數值天氣預報在火炮氣象保障中的應用極大縮短了氣象保障的準備時間[2-5],但是,初始場測量處理誤差和數值模式建模誤差,使得數值預報結果中含有較大的預報誤差,且尤以風的預報誤差最為顯著[6]。現行有效的數值修正方法以數值天氣預報的預報誤差及其變化規律為依據,對臨近天氣預報的預報誤差進行數值修正[7],提升氣象要素的預報精度。因此,如何快速準確獲取預報誤差已成為提升彈道解算用數值天氣預報的預報精度需首要解決的問題之一。

目前,利用成熟的火炮外彈道跟蹤觀測技術獲取的實測彈道數據,為快速準確獲取彈道解算用數值天氣預報的預報誤差提供了新途徑。本文為獲取風的預報誤差,使用風修正系數描述風的預報誤差,提出一種采用無跡卡爾曼濾波算法,直接從實測彈道數據和原始預報氣象數據中辨識風修正系數的方法,并通過數值比對和彈道重構,對風修正系數的辨識精度進行分析。

1 系統模型

1.1 WRF模式簡介及參數設置

WRF(weather research and forecast,WRF)模式是由美國多家科研機構于2000年開發的新一代中尺度數值模式和數據同化系統,其廣泛應用于中小尺度到全球尺度的數值預報和大氣模擬,并可提供指定區域在未來時段內的時空網格化氣象數據。

本文中WRF模式預報區域位于我國東北地區的松嫩平原,該區域為溫帶大陸性季風氣候,太陽輻射充足。模式水平方向上采用單重網格結構,格點數為121×121,格點間距為4 km,垂直方向上分為81層,模式頂層氣壓為1 000 Pa,初始場使用NCEP發布的分辨率為0.25°×0.25°的再分析資料,積分步長為15 s,預報時長為4 h。

1.2 假設條件

影響彈丸飛行狀態的氣象要素包括氣壓、虛溫、縱風和橫風,為了具體分析彈道解算用數值天氣預報的氣象保障效果,本文以WRF模式的短時預報為例,一方面使用均方根誤差、平均絕對誤差和誤差標準差[8]對WRF模式預報的氣象要素進行檢驗,另一方面,基于外彈道仿真,分析WRF模式中單一氣象要素的預報誤差對彈丸飛行狀態的影響。其中,預報氣象數據和實測氣象數據描述的均為該地2019年12月14日12時的高空大氣狀態,外彈道仿真則使用某型榴彈的六自由度剛體彈道模型,射角為51°,射向為100.487°,射程約為30 km。WRF模式預報氣象要素的檢驗結果如表1所示,WRF模式單一氣象要素的預報誤差對彈丸飛行狀態影響的分析結果如表2所示。

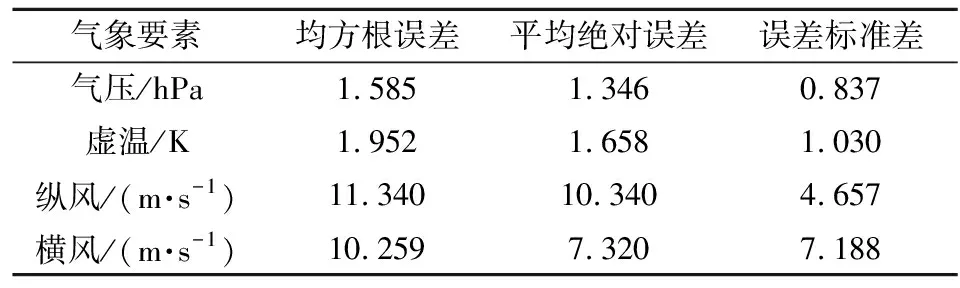
表1 WRF模式預報氣象要素檢驗結果

表2 彈丸飛行狀態偏差均值表

由表1和表2可得,相比于風的預報誤差,氣壓和虛溫的預報誤差及其離散程度以及預報誤差引起的彈道偏差均相對較小,因此,本文只將風修正系數作為待辨識參數,并忽略氣壓和虛溫的預報誤差對辨識風修正系數的影響,故本文做出如下假設:

①忽略氣壓和虛溫的預報誤差對辨識風修正系數的影響;

②風修正系數在辨識區間內為常值。

1.3 彈道模型

為了從實測彈道數據和原始預報氣象數據中辨識風修正系數,需構建彈丸運動模型,建立實測彈道數據與氣象數據之間的聯系。考慮到目前彈道跟蹤觀測數據主要以位置和速度為主,本文選用質點彈道模型,此彈道模型在有風條件下的彈道方程[9]為

(1)

式中:

x、y、z,vx、vy和vz分別為彈丸在發射坐標系下的坐標分量和速度分量;m,d,l和JC分別為彈丸質量、彈丸直徑、彈丸長度和彈丸極轉動慣量;Cx,C′y,m′z和m′xz分別為空氣阻力系數、升力系數導數、靜力矩系數導數和極阻尼力矩系數導數;p,Tv,wx,wz,vs,Rd和k分別為當地氣壓、當地虛溫、當地縱風、當地橫風、當地聲速、干空氣氣體常數和比熱比;kL和kC分別為縱風修正系數和橫風修正系數;g,v0,s和η分別為當地重力加速度、標定初速、彈道弧長和膛線纏度。

2 無跡卡爾曼濾波算法辨識風修正系數

為了實現從非線性彈道模型中辨識風修正系數,本文將無跡卡爾曼濾波算法作為辨識算法。由卡爾曼濾波穩定性原理[10]可知,如果濾波穩定,估計值和估計均方誤差將隨濾波時間的增長逐漸不受濾波初值的影響,并最終收斂,實現無偏估計。但是,每個估計值和每個估計均方誤差的收斂速度不同,若濾波時間較短,可能存在估計值和估計均方誤差沒有完成收斂的情況。因此,本文將原始預報氣象數據作為彈道模型的基礎氣象條件,采用無跡卡爾曼濾波算法對實測彈道數據進行迭代處理,并將每次迭代所得風修正系數和狀態變量的估計均方誤差作為下次迭代的初值,直至滿足迭代終止條件,其流程如圖1所示。

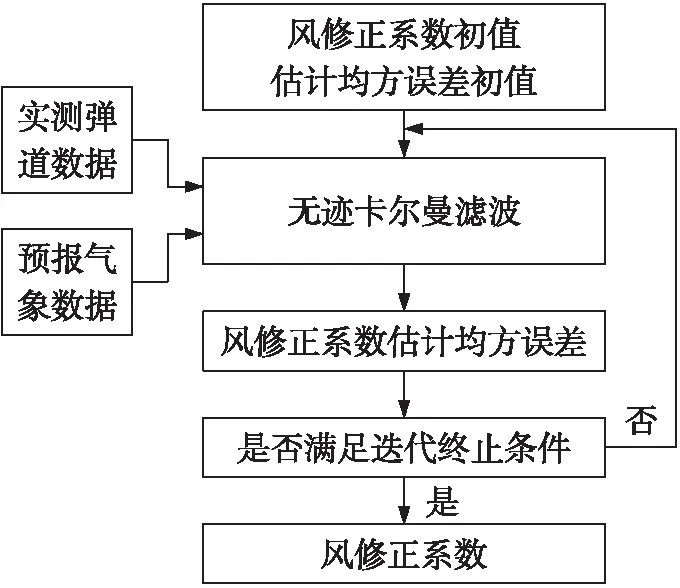
圖1 無跡卡爾曼濾波算法辨識風修正系數流程圖

由式(1)和實測彈道數據的種類可知,無跡卡爾曼濾波算法中的觀測變量為x、y、z,vx、vy、vz,狀態變量為x、y、z,vx、vy、vz、kL和kC,即:

Z=(xyzvxvyvz)T

(2)

X=(x1x2x3x4x5x6x7x8)T=

(xyzvxvyvzkLkC)T

(3)

將式(3)代入式(1),得:

(4)

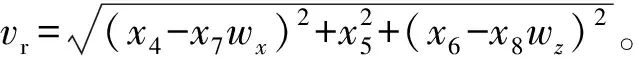
結合圖1,無跡卡爾曼濾波算法辨識風修正系數的主要步驟如下。

①第1步。選定初值。

②第2步。無跡卡爾曼濾波計算,詳細計算步驟可參考文獻[10]。

③第3步。判斷是否滿足迭代終止條件,若沒有滿足,則返回第2步。為了提高迭代效率,本文設置2個迭代終止條件,條件一為達到最大迭代次數nmax,條件二為連續2次迭代所得縱風修正系數之差εL和橫風修正系數之差εC均小于給定閾值。

為了提升辨識結果精度,減小包括氣動參數誤差和起始擾動誤差在內的其他誤差對辨識結果的影響,本文將彈丸風洞吹風數據作為彈道模型中氣動參數的真值,并將多組辨識結果的平均值作為最終的辨識結果。

3 數值計算與分析

為了檢驗無跡卡爾曼濾波算法辨識風修正系數的效果,本文基于某實測彈道數據和WRF模式原始預報氣象數據對其進行數值分析,相關參數設計如下。

①實測彈道數據的位置誤差(DRMS,68%):水平10 m,垂直10 m;速度精度(DRMS,68%):水平0.2 m/s,垂直0.5 m/s;

②彈道數據選擇距地面5 200～6 800 m的降弧段彈道數據;

③WRF模式參數設置與第1.1節中的參數設置相同;

④無跡卡爾曼濾波算法迭代終止條件一為最大迭代次數nmax=200,迭代終止條件二為連續2次迭代差值εL<0.000 1且εC<0.000 1。

基于上述參數,本文以其中一組實測彈道數據為例,在辨識過程中x、y、z的估計均方誤差隨迭代次數n(取前10次,下同)的變化如圖2所示,vx、vy、vz的估計均方誤差隨迭代次數的變化如圖3所示,kL、kC的估計均方誤差隨迭代次數的變化如圖4所示,kL、kC隨迭代次數的變化如圖5所示。

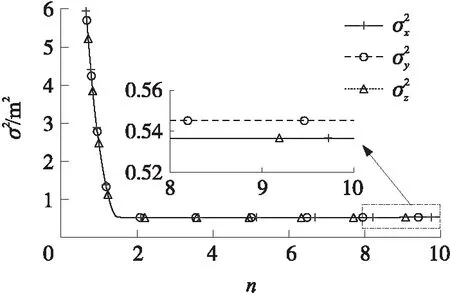
圖2 迭代過程中的位置估計均方誤差

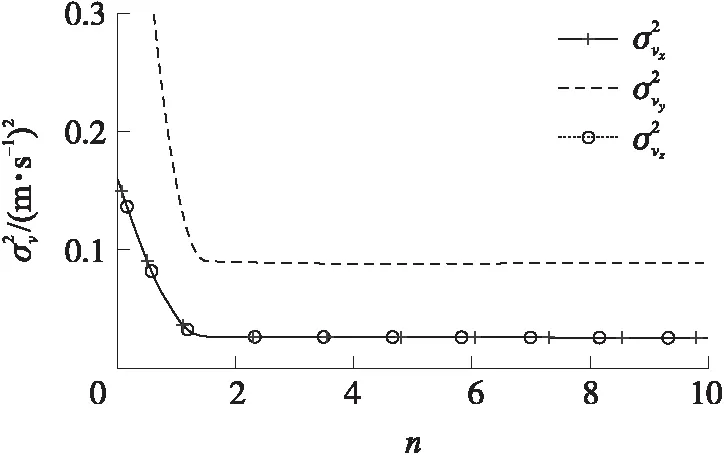
圖3 迭代過程中的速度估計均方誤差

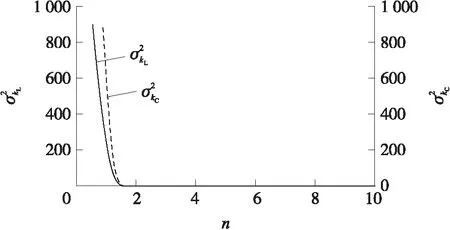
圖4 迭代過程中的風修正系數估計均方誤差

將3組辨識結果取平均值作為該辨識區段內的辨識結果,即辨識的縱風修正系數為2.084 056,橫風修正系數為1.254 748。實測的風修正系數如表3所示,使用加權平均值(權重由彈丸在每個高度段內的飛行時間確定,下同)代表實測的風修正系數,即實測的縱風修正系數為1.944 045,橫風修正系數為1.206 837。

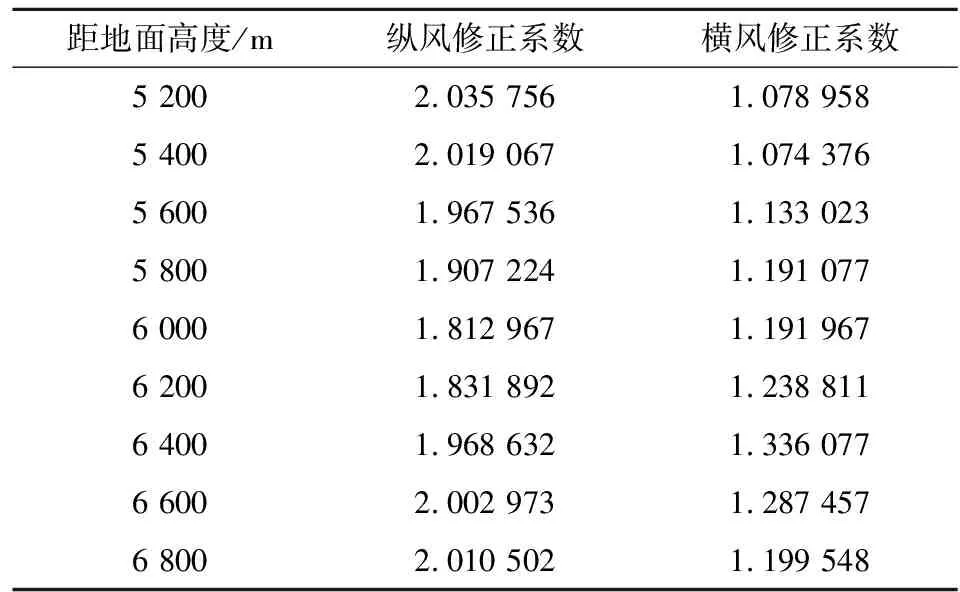
表3 實測的風修正系數

將實測的風修正系數和辨識的風修正系數進行對比可得,辨識的縱風修正系數和橫風修正系數的相對誤差分別為7.20%和3.97%,產生上述誤差的原因可能如下:一是辨識過程中未考慮氣壓和虛溫的預報誤差對辨識風修正系數的影響,將氣壓和虛溫的預報誤差折算入風修正系數當中;二是彈道模型誤差,結合六自由度剛體彈道模型可知,狀態變量還受彈丸姿態角等因素的影響,而質點彈道模型未考慮這些因素;三是實測氣象數據與實測彈道數據時空不匹配。

原始預報氣象數據和實測氣象數據描述的均為同一時刻且同一地點的高空大氣狀態,利用前文辨識所得的縱風和橫風的修正系數對原始預報氣象數據中的風進行修正,得到修正預報氣象數據,3種氣象數據中風的加權平均值如表4所示。

表4 彈道區段內風的加權平均值

由表4可得,原始預報氣象數據中的縱風和橫風經修正后,其誤差分別減小85.19%和79.27%。

分別使用原始預報氣象數據和修正預報氣象數據對位于距地面5 200～6 800 m的降弧段彈道進行重構,2種重構的彈道段和濾波處理的實測彈道段在x-y平面的投影如圖6所示,在x-z平面的投影如圖7所示,在z-y平面的投影如圖8所示,2種重構的彈道段與濾波處理的實測彈道段間的狀態均方根誤差如表5所示。

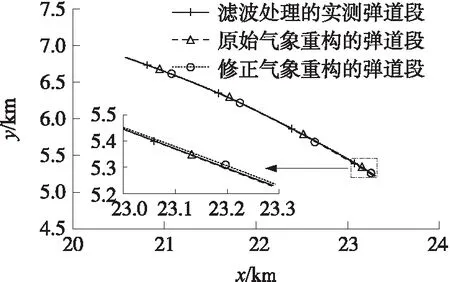
圖6 重構彈道段在x-y平面的投影

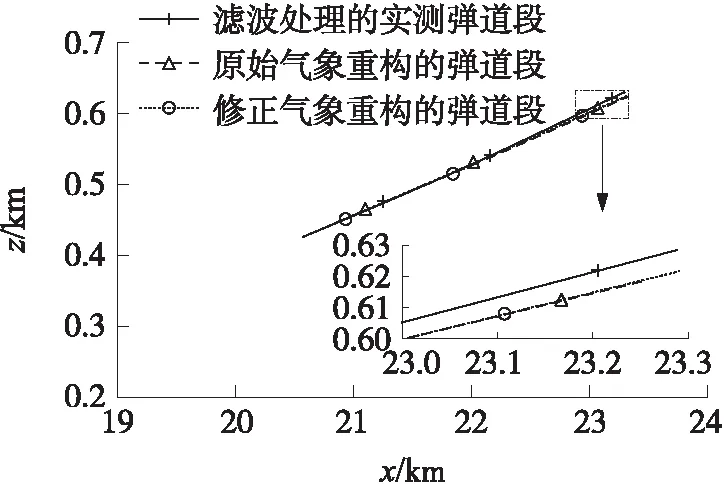
圖7 重構彈道段在x-z平面的投影

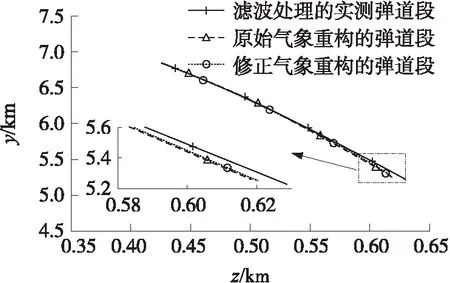
圖8 重構彈道段在z-y平面的投影

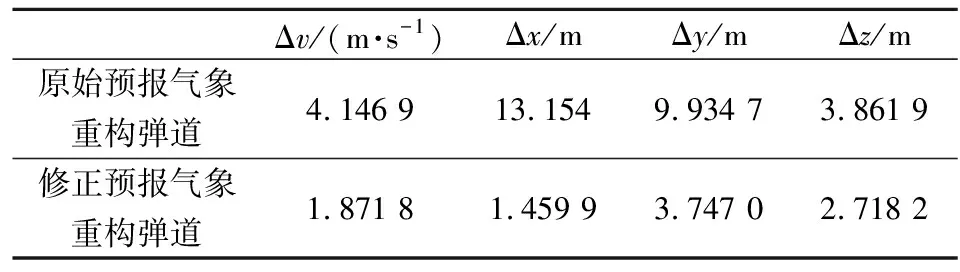
表5 重構彈道段的狀態均方根誤差

由圖6～圖8及表5可得,修正預報氣象重構的彈道段相比原始預報氣象重構的彈道段而言,更加接近于濾波處理的實測彈道段,因此,修正預報氣象比原始預報氣象對真實氣象的描述更為準確,從而說明辨識所得風修正系數的精度較高以及修正彈道解算用數值天氣預報的預報誤差是必要的。

4 結束語

本文將原始預報氣象數據作為基礎氣象條件,采用無跡卡爾曼濾波算法從實測彈道數據中辨識風修正系數,通過對實際辨識結果進行分析,得出以下結論:該方法辨識所得風修正系數具有較高的精度,可作為彈道解算用數值天氣預報的預報誤差,實現對臨近天氣預報的數值修正,滿足工程應用需求;無跡卡爾曼濾波算法在辨識風修正系數的過程中兼有濾波功能,能夠在一定程度上減小噪聲對辨識結果的影響。本文研究結果可以為提升彈道解算用數值天氣預報的預報質量提供一定的理論參考。