某小口徑槍械內彈道時期槍管的動態響應研究

方義川,王永娟,孫國旭

(1.南京理工大學 機械工程學院,江蘇 南京 210094;2.內蒙古北方重工業集團有限公司 南京研發中心,江蘇 南京 211100)

槍管是自動武器的關鍵部件,內彈道時期其受到高溫、高壓以及高速彈丸的載荷作用會產生變形和振動,這對于槍管壽命以及射擊精度會產生顯著影響[1-2]。因此掌握內彈道時期槍管的動態響應規律對于推動自動武器結構設計由傳統的靜態設計向動態設計轉變具有重要意義。

在槍管的熱彈耦合響應方面,徐寧等[3]通過建立轉管機槍槍管的有限元模型,比較熱載荷單獨作用、膛壓載荷單獨作用以及熱彈耦合作用條件下的計算結果,說明熱載荷對于槍管耦合應力響應影響較大,且軸向、周向和徑向的響應規律存在差異;文獻[4-5]在溫度響應分析的基礎上,將非均勻溫度場作為熱力學邊界條件對身管進行熱彈耦合分析。現有研究在計算熱彈耦合響應時,大多不考慮軸向熱傳遞的邊界條件,這與實際的三維模型存在較大的差異性。在槍管的振動方面,劉國慶等[6]采用非線性有限元方法建立了運動步槍的彈/槍相互作用模型,計算得到了槍口的橫向振動規律;周齊鄭等[7]將火炮身管簡化為Bernoulli-Euler均勻等截面懸臂梁,采用小參數法求解得到了單發彈丸激勵下身管振動方程的近似解;于情波等[8]同樣將身管簡化為變截面懸臂梁,建立了以振動理論為基礎的彈槍耦合有限元動力學模型。現有模型大多針對彈/槍相互作用或將身管簡化為懸臂梁進行槍管振動響應計算,未考慮槍管組件在射擊過程中與架座、機匣、導氣裝置或其他組件的相互作用,與實際的約束情況存在差異。

上述研究的某些結果并非完全適用于自動步槍的槍管動態響應。本文基于數字圖像相關法理論[9],采用3D-DIC試驗方法采集槍口狀態,進行數據處理分析,建立內彈道時期基于隨動邊界的槍管熱彈耦合有限元模型和槍管振動有限元模型,通過對比仿真獲得的槍口理論計算結果與試驗結果來研究小口徑槍械在內彈道時期的槍管動態響應規律。

1 基于3D-DIC的槍口狀態試驗研究

試驗數據采集基于的基本方法為數字圖像相關法(digital image correlation,DIC),其基本原理可以分為4步:采集未變形的參考圖像,采集變形后的圖像,劃分子區,尋找相關性進行計算。其中3D數字圖像的相關性函數定義為

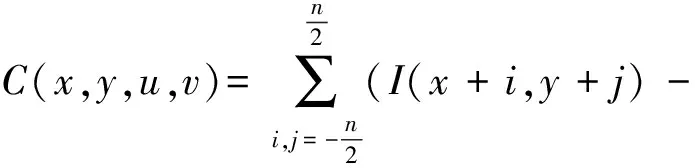
I*(x+u+i,y+v+j))2

式中:C(x,y,u,v)為圖像的相關性函數;x,y為像素點的坐標值;u,v為像素點的位移值;n為子區的大小;I(x+i,y+j)和I*(x+u+i,y+v+j)分別為變形前和變形后的圖片。DIC方法的基本原理如圖1所示。

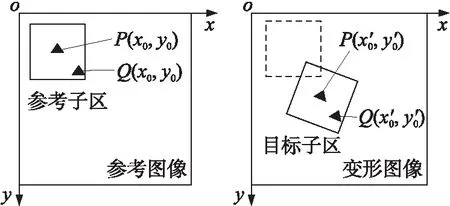
圖1 DIC方法的基本原理

試驗采用2臺Photron高速攝像機配上定焦鏡頭,基于VIC-Snap軟件的驅動,采用紅外觸發在center模式下進行信號的同步采集,相機的拍攝幀率設定25 000 s-1,通過VIC-3D軟件的計算能夠獲取槍管振動狀態和應變的信息。試驗過程可以分為4步:在去除膛口裝置的槍管外壁部分制作散斑,對相機進行標定,按照射擊規范進行試驗采集圖像,保存采集數據進行分析計算。試驗方案和部分試驗裝置實物如圖2和圖3所示。

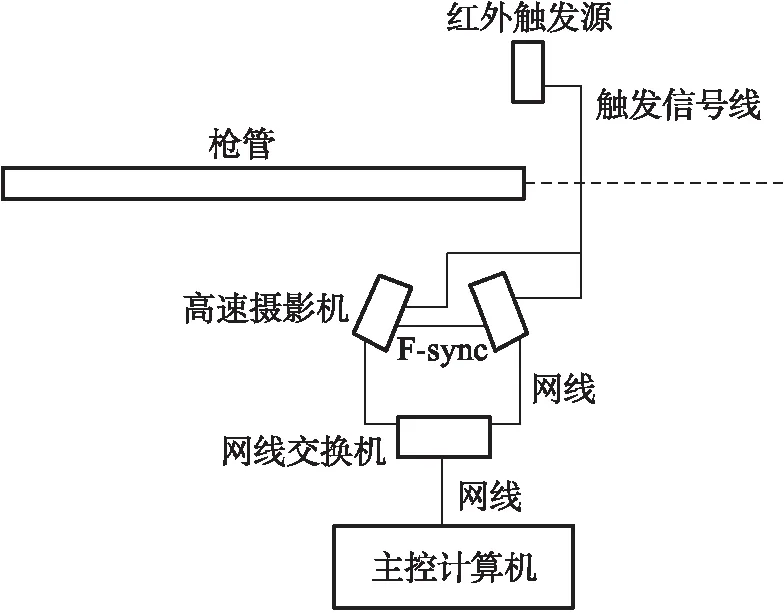
圖2 試驗方案

圖3 3D-DIC數據采集系統

3D-DIC數據采集系統包括自動步槍和槍架、槍口外壁的散斑涂層、高速攝像機、紅外觸發器和補光燈。步槍發射產生的槍口焰被紅外觸發器捕捉并產生觸發信號,高速攝像機依據計算機設定的觸發模式進行數據采集,采集后軟件根據2臺攝像機的采集結果處理得到位移、應變、應力等信息。

在3D-DIC軟件中設置分析區域合適的子區域大小,使攝像機在追蹤圖像分析區域之間的位移變化時能夠確保子區域內的散斑可以在不同的圖像之間被識別。本次研究計算步長設置為2,計算過程中軟件將對分析區域中橫向與縱向每間隔一個像素點計算一次。針對槍口參考點,為了降低結果的偶然性,實際計算時選取包圍該參考點的一個小圓,通過取計算范圍內像素點結果的平均值作為參考點的計算結果。后處理選取的分析區域和參考點C0如圖4所示。

圖4 分析區域AOI與槍口參考點

定義:以槍管尾端面中心為原點,槍管軸線方向為X方向,槍口指向為正;豎直方向為Z方向,向上為正;Y方向可由右手系原則確定。此時槍口參考點位置坐標可表示為(435 mm,6.75 mm,0)。在相同的試驗條件下,采用單發射擊方式進行5次重復試驗,得到了內彈道時期槍口參考點的三維運動軌跡如圖5所示。

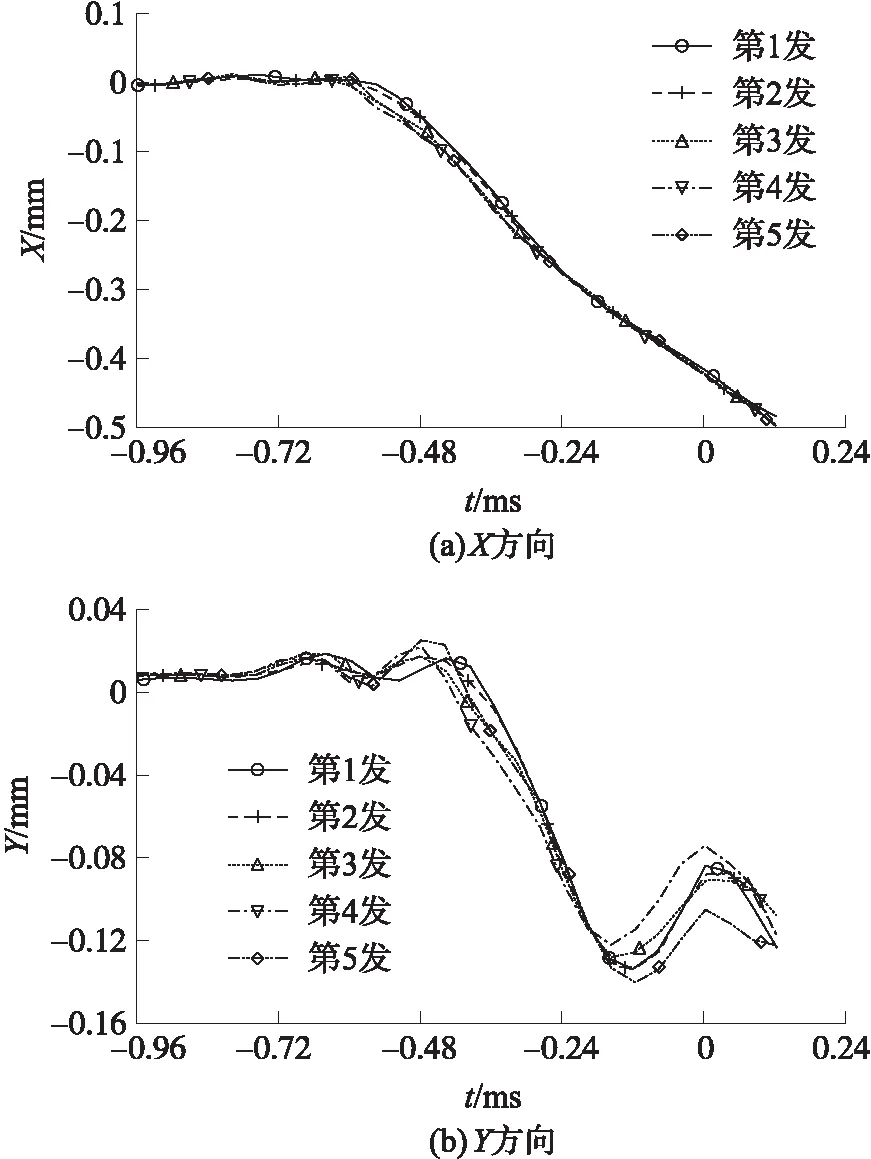
圖5 內彈道時期槍口參考點的三維運動采集結果

圖5中0時刻對應彈丸出膛瞬間,試驗結果表明:彈丸出膛前槍口就已經開始振動,此振動是X、Y、Z3個方向耦合的結果。在豎直方向上,槍口參考點先小幅向上運動,之后大幅向下運動,達到峰值后開始回彈,彈丸在槍口回彈的過程中出膛。槍口參考點的運動軌跡大部分位于第Ⅶ卦限,彈丸出膛時槍口參考點也位于第Ⅶ卦限。5次試驗的結果具有較高的重復性和一致性,說明試驗結果的規律是可靠的、科學的。

2 隨動邊界條件下槍管的應力響應研究

2.1 槍管熱彈耦合有限元模型的建立

內彈道時期,槍管彈后區域受到高溫高壓火藥燃氣的作用,作用區域隨著彈丸的運動不斷擴大。氣體壓力垂直作用于槍管內壁以及彈丸底面,槍管內壁與高溫火藥氣體間存在強迫對流,槍管外壁與空氣存在自然對流,熱量以熱傳導方式在槍管內部傳遞。內彈道時期槍管受熱載荷以及膛壓載荷作用的模型如圖6所示。

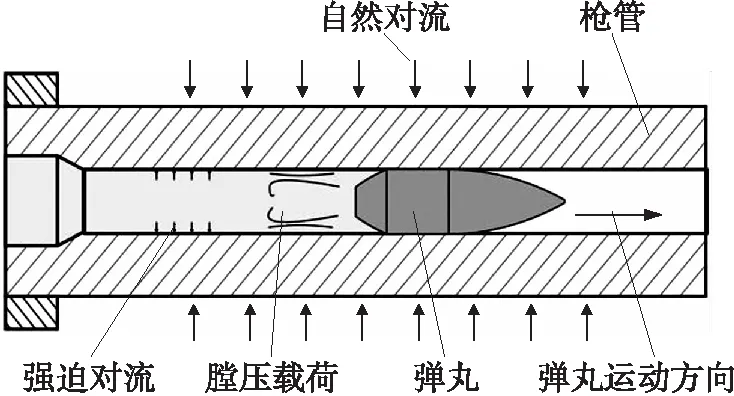
圖6 內彈道時期槍管受載模型

對本次研究的槍管劃分網格,得到的模型單元數為100 338,節點數為119 154,采用八節點線性傳熱六面體單元(DC3D8)計算溫度場,采用八節點線性六面體減縮積分單元(C3D8R)計算三維應力場。由于槍管內壁采用鍍鉻工藝,鉻層具有一定厚度,因此在進行熱傳遞計算時需要對鍍鉻層的網格進行必要的加密處理。由于溫度分布的不均勻性會影響槍管的應力應變場,而溫度場自身的分布則不會受到槍管應力應變場變化的影響,所以采用有限元軟件提供的順序熱彈耦合的方式建立有限元模型,首先通過傳熱計算獲取溫度場的分布結果,隨后將得到的溫度場結果與膛壓載荷作用耦合,計算得到槍管的熱彈耦合響應結果。仿真計算相關材料參數如表1所示。

表1 材料參數表

2.2 隨動邊界的確定

考慮到火藥燃氣密封于彈后空間,一方面膛壓大小會隨著彈丸的運動發生變化,另一方面彈丸的運動還會使火藥燃氣與槍管內壁作用的區域發生變化。為了在數值模型中體現上述隨動邊界條件,在有限元軟件中需要借助用戶子程序完成邊界條件的施加。內彈道邊界條件的時變曲線如圖7所示。

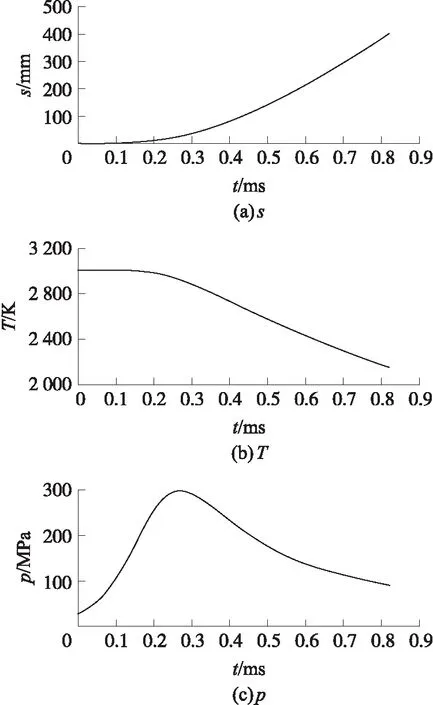
圖7 內彈道邊界條件的時變曲線

每一個載荷增量步,用戶子程序被調用,主程序將該步中彈丸位移參數傳送至子程序中進行判斷,若判斷“積分點坐標小于彈丸位移”為真,即表示該積分點位于彈后空間,子程序則將利用主程序中存儲的火藥燃氣時變參數、材料的物性參數以及環境邊界條件等參數為當前積分點賦值;若判斷“積分點坐標小于彈丸位移”為假,即表示該積分點位于彈前空間,火藥氣體和槍管內壁不發生作用,子程序將直接為該積分點賦值環境溫度和大氣壓強等其他初始參數。重復以上過程直至所有積分點均被賦值。子程序實現隨動邊界的過程如圖8所示。

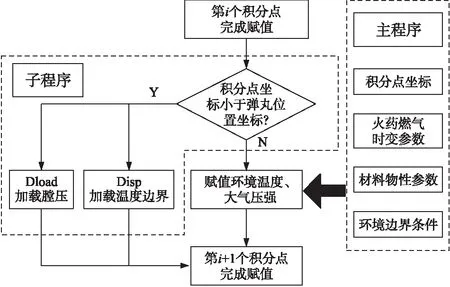
圖8 子程序實現隨動邊界的過程

2.3 槍管的應力響應分析

為了更清晰地觀察槍管內壁的應力響應,取槍管的縱截面,即可獲取不同時刻下基于隨動邊界條件的熱力耦合計算所得的槍管應力響應,如圖9所示。

圖9 熱彈耦合條件下槍管的應力響應(單位:MPa)

由圖9可以看出,小口徑自動步槍單發射擊時,槍管受到膛壓和熱沖擊同時作用,其應力響應隨著槍彈的運動會發生明顯的變化。槍管在彈后空間的應力沿軸向呈梯度分布,這主要是因為膛壓和熱沖擊載荷均為時變載荷,邊界的改變不僅使得槍管內壁在不同時刻產生明顯的時程響應,而且在同一時刻的應力響應沿軸線方向也不均勻。對于彈前空間來說,由于尚未受到膛壓和熱沖擊載荷的作用,不會產生明顯的應力響應,這與實際的物理場也是吻合的。

由于槍管材料的變形仍屬于彈性形變的范疇,因此根據測試得到的應變曲線和材料的楊氏模量,得到了槍口外壁參考點的VonMises應力響應σ,如圖10所示,圖中,N為拍攝幀數。

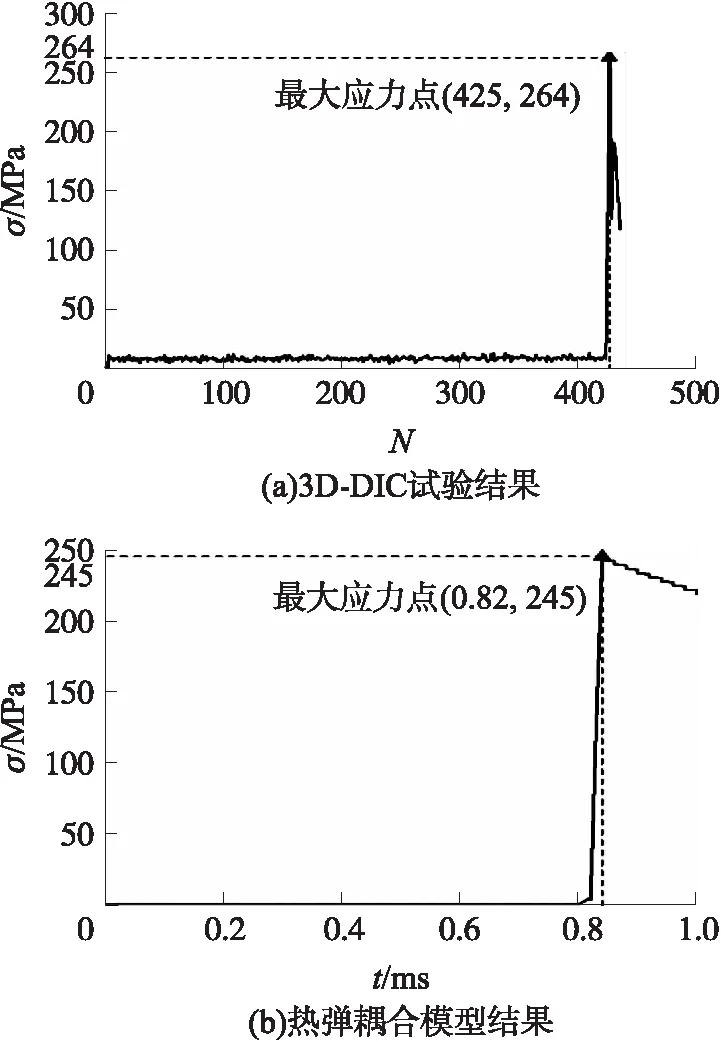
圖10 槍口外壁參考點的應力響應

通過對比3D-DIC試驗結果和有限元計算結果可知:3D-DIC試驗測得槍口外壁Mises應力響應在內彈道結束時響應峰值為264 MPa,熱彈耦合模型的計算結果為245 MPa,二者的誤差為7.2%,說明本文建立的熱彈耦合模型能較為準確預測實際載荷情況下槍管的應力響應。為了進一步定量分析槍管內壁的應力響應,在槍管內壁取4個積分點A、B、C、D,坐標分別為XA=15 mm,靠近槍管尾端面;XD=420 mm,靠近槍管口部;XB=120 mm,XC=240 mm,位于A點和D點之間,其應力的時程響應如圖11所示。

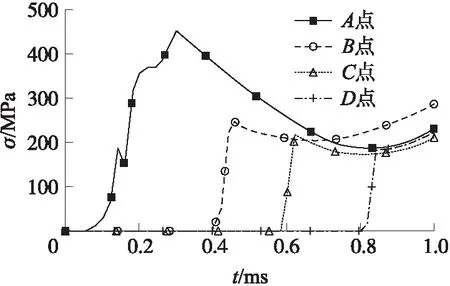
圖11 熱彈耦合條件下單點應力響應時程曲線

從圖11可以看出,隨著彈丸的運動,在膛壓和高溫熱沖擊同時作用于槍管內壁的瞬間,內壁會立即產生一個較大的應力響應:A點在0.3 ms時達到應力峰值σA,max=450 MPa,B點在0.46 ms時達到應力峰值σB,max=246 MPa,C點在0.62 ms時達到應力峰值σC,max=219 MPa,D點在0.82 ms時達到應力峰值σD,max=188 MPa,并且滿足σA,max>σB,max>σC,max>σD,max的關系。內壁節點處的相關參數如表2所示。

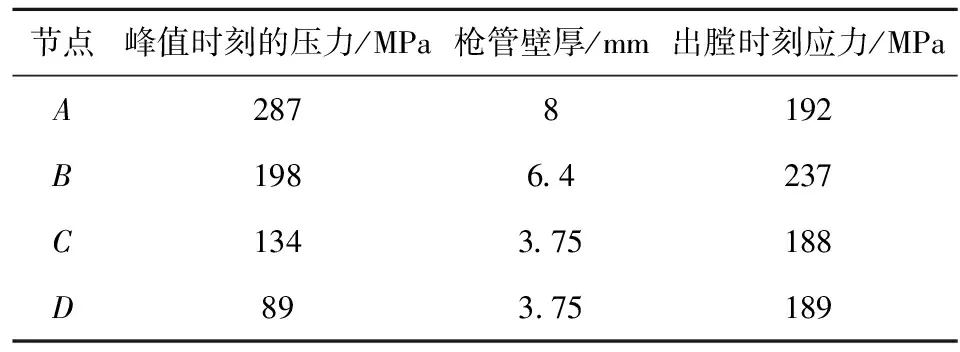
表2 內壁節點處的相關參數

對比膛壓曲線的數值與4個積分點的應力響應結果可知,熱沖擊載荷的介入會顯著提高內壁材料的應力響應峰值。此外,內壁積分點的應力響應達到峰值之后,不會隨著膛壓載荷的持續衰減而隨之衰減,A點、B點和C點均在應力響應衰減一段時間后逐漸提高,這是由于隨著熱載荷的持續作用,熱應力的作用效果能夠補償因膛壓下降造成的應力響應衰減,達到平衡狀態后會使應力響應開始增加。D點的膛壓衰減較大,而應力響應并未出現衰減段。因此在考慮槍管強度和槍管壽命問題時,熱載荷是一個不可忽略的重要因素。

注意到各點應力響應第二次增加的過程,對比各個積分點在出膛時刻的應力響應,存在如下關系:σB>σA>σC≈σD。由于B處的管壁較C和D而言更厚,熱應力在后續階段的作用效果更為明顯,壁厚越大,后期應力響應越大。而對于A點,由于考慮節套部分,壁厚雖然最大,但冷卻更快,所以出膛時刻應力并不是最大。

3 槍管振動響應研究

3.1 槍管振動的有限元模型

將3D-DIC試驗中的裝置在三維軟件中建模后,導入有限元分析軟件中,劃分四面體網格,槍管與節套、槍管與導氣箍為過盈配合連接,節套與下機匣、下機匣與架座采用銷連接。對槍機與節套的相互作用進行簡化,采用模擬閉鎖機構承受膛壓載荷,并傳遞到節套相應的閉鎖支撐面上,為了保證計算的精確度,對在配合面附近的網格進行了加密處理,網格總數為103 546。步槍發射系統的有限元模型如圖12所示。

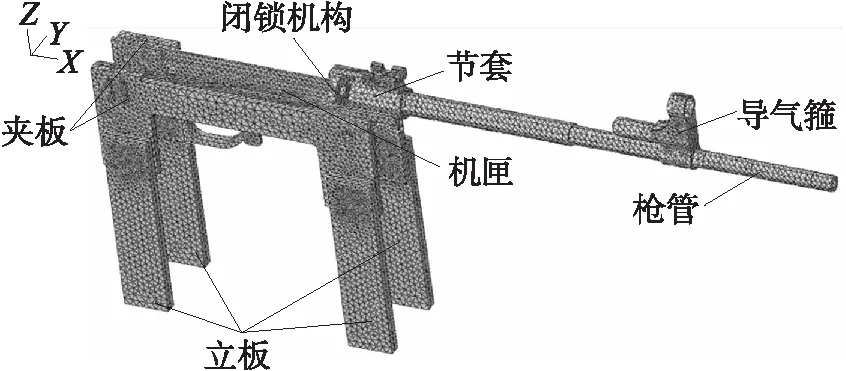
圖12 步槍發射系統的有限元模型

將槍管材料、節套材料和架座材料、導氣箍材料和閉鎖機構材料按照高強度鋼計算,下機匣材料按照鋁合金計算,材料相關的力學性能參數如表3所示。

表3 材料相關的力學性能參數

對于導氣式武器來說,載荷主要考慮膛壓載荷、氣室壓力載荷以及重力載荷。本文根據布拉文經驗公式,編制氣室壓力計算程序,得到載荷的時變規律如圖13所示。

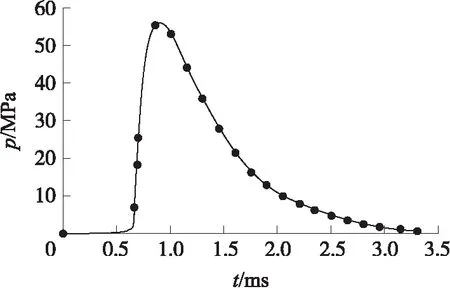
圖13 導氣室壓力的時程變化曲線

相互作用屬性中,面與面的接觸控制算法采用罰函數法和硬接觸,防止從面節點對于主面的穿透。邊界條件設置為4個立板的底面完全固定,與試驗的約束情況一致。彈丸發射前試驗裝置在重力的作用下處于靜平衡狀態,屬于靜態問題,此時槍管的彎曲變形適合采用隱式算法求解;膛壓載荷和氣室壓力作用時,伴隨瞬態較大的接觸力和變形,屬于瞬態問題,適合采用顯式算法求解。因此,實際計算時,將采用隱式算法求解得到的靜態結果導入顯式求解器,并將其作為瞬態問題求解的初始條件,能夠充分發揮顯、隱式算法的優勢,使得計算過程更貼近于實際情況,以提高有限元計算結果的準確性。

3.2 有限元計算結果分析

通過顯隱式混合運算,后處理中將變形系數設置為20,觀察槍管和節套在彈丸出膛時刻的動態響應,如圖14所示。

圖14 節套槍管的振動狀態

結果表明,內彈道時期槍管的位移動態響應大致可以分為3個階段。在0～0.3 ms時,盡管膛壓載荷已經接近峰值,但槍管橫向并未產生明顯的動態響應,只是沿槍管軸線方向產生了位移響應,因此槍口部分幾乎不會產生橫向振動;0.3～0.6 ms時,膛壓載荷持續衰減,此時槍管發生彎曲變形,靠近藥室部分的槍管橫向振動幅值較大,并向槍口部傳遞,槍口部分迅速向下彎曲,并在0.6 ms時達到最大后回彈;0.6～0.82 ms時,0.82 ms時刻彈丸出膛,槍管口部在此過程中發生小幅度回彈,槍管整體仍存在較大的彎曲變形,變形峰值處于槍管中部,尚未傳遞至槍口,彈丸出膛時槍口部分豎直位移為負,但槍口部分與水平方向的夾角為正。

提取槍口外壁參考點的計算結果,并將內彈道時期槍口位移的動態響應有限元結果與試驗中參考點數據進行對比,如圖15所示。

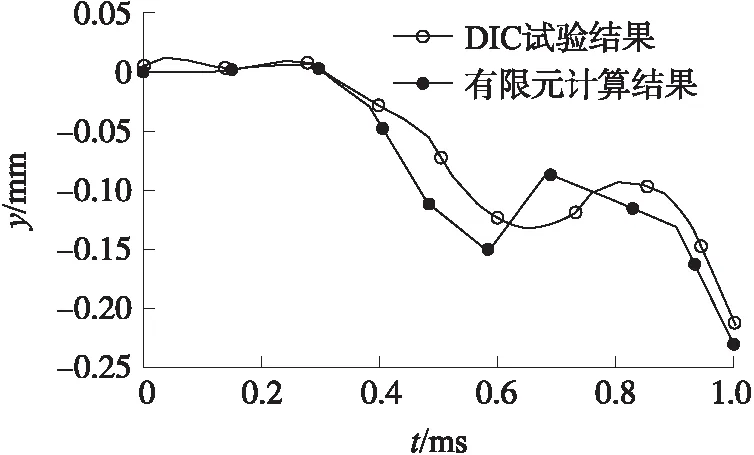
圖15 槍口外壁有限元結果與試驗對比

通過圖15可以看出,有限元計算結果和試驗結果基本吻合,均體現了槍口外壁在內彈道時期的動態響應。槍口在0.3 ms左右迅速向下振動,在0.6 ms處達到負向的峰值,有限元計算結果的峰值大小為-0.155 mm,試驗結果為-0.145 mm(誤差6.45%),達到峰值后開始回彈,回彈并未完全抵消第一階段的槍管下垂,達到回彈峰值后槍管口部繼續向下振動,彈丸在此過程中出膛,出膛時對應的振動幅值有限元計算結果為-0.12 mm,試驗結果為-0.105 mm(誤差為12.5%)。數值計算模型得到的規律在總體趨勢上與試驗一致,與試驗曲線的對比結果也驗證了模型的正確性和有效性。

3.3 槍口動態響應與射彈散布預測

對于射彈散布的計算可以采用面向射彈散布的槍械協同仿真模型[10]。該模型主要結合經典內彈道方程組、彈/槍相互作用有限元模型以及質點外彈道模型對槍械射擊精度進行預測。本文對于該計算模型進行簡化,利用所建立的有限元模型中提取到的輸入參數來計算彈丸的落點,并與試驗測試的彈著點進行比較。簡化后的槍械協同仿真模型主要由內彈道模型、槍管動態響應有限元模型以及質點外彈道模型組成,協同仿真模型的參數傳遞過程如圖16所示,槍管振動有限元模型輸出參數如表4所示。表中,v0為由內彈道方程組計算得到的彈丸初速;X,Y,Z,vx,vy,vz分別為槍口在彈丸出膛時刻各個方向上的位移和速度;θh,θv分別為槍管在彈丸出膛時刻在XY平面上和XZ平面上的轉角。

當細白的蟹肉與Bin311在舌尖上不期而遇，便開始成就一場味蕾的盛宴：霞多麗清新而爽口的果香，彌漫著桃子與梨皮的氣息，化解了蟹膏的濃膩，唇齒留香；冷涼產區溯源地的葡萄提供了脆爽而持久的酸度，不僅解膩而且還提升了蟹的鮮美；經由橡木桶的“畫龍點睛”而呈現出燧石的復雜度與乳脂般質地的酒體，更是與蟹的甜美交相呼應并將其所有的鮮味喚醒，令人愉悅。一眨眼的功夫，佐以干白，幾屜蟹便已全部食得干凈，回味無窮。

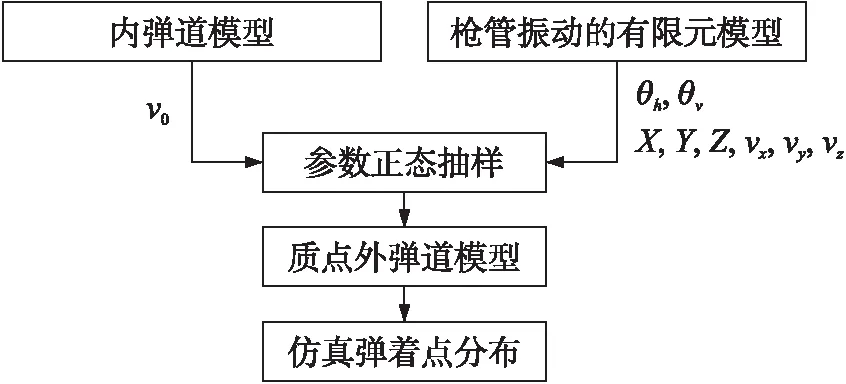
圖16 簡化后的槍械協同仿真模型參數傳遞

表4 槍管振動有限元模型輸出參數

射擊過程具有隨機性,槍管的動態響應本質上是一個隨機過程,對于相應的隨機因素在正態分布范圍的抽樣方法參考文獻[10],抽樣結果需要進行Shapiro-Wilk正態校檢[11]以保證抽樣的科學性,將抽樣后的結果代入質點外彈道模型即可實現對于彈丸落點的隨機模擬。以彈丸初速為例,其20組抽樣結果與正態校驗結果如圖17和表5所示。

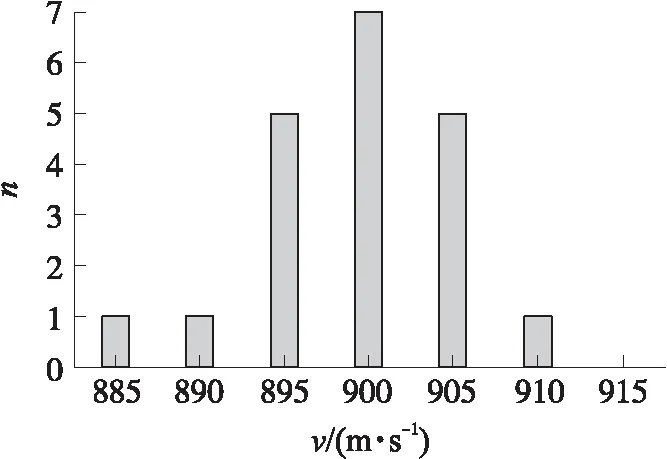
圖17 彈丸初速分布直方圖

表5 彈丸初速統計表

試驗中冷槍射擊的28發射彈在100 m立靶處的散布結果如圖18(a)所示,仿真中取20組參數隨機抽樣模擬得到的100 m立靶散布結果如圖18(b)所示。

圖18 理論彈丸落點與試驗彈丸落點的對比

通過對比可知,試驗所得單發的試驗散布為53 mm,仿真結果為55.9 mm,二者相對誤差為5.2%,對比結果進一步驗證了前述槍管振動有限元模型的準確性,也說明了運用本文建立的槍口振動有限元模型與協同仿真模型可以預測槍械單發射擊散布。

4 結束語

將3D-DIC槍口狀態采集試驗結果與有限元模型計算結果進行比較,得到如下結論:

①隨動邊界條件導致了槍管的應力響應沿著軸線方向存在極大的不均勻性,彈前空間幾乎沒有響應,彈后空間在隨動邊界條件施加后迅速達到響應峰值,而后衰減;

③內彈道時期槍口振動響應大致可以分為下垂—回彈—下垂3個部分,回彈幅度并未完全抵消初次下垂效果,彈丸在回彈峰值之后出膛,出膛時槍口部分豎直位移為負,但與水平方向的夾角為正;

④將正態抽樣后的槍口狀態參數代入簡化后的協同仿真模型中進行隨機模擬,得到的100 m立靶射彈散布結果與試驗散布結果接近,表明本文建立的有限元模型結合簡化后協同仿真模型能較好地預測100 m立靶單發射彈散布。