利用人工神經網絡進行紋樣重構與創新

沈淑敏，施清清，孫夢潔，林 麗，陶 晨

(紹興文理學院 紡織服裝學院，浙江 紹興 312000)

紋樣是紡織品的重要構成要素之一，紋樣的數字化和自動化生成，是紡織紋樣領域的研究熱點。目前，數字化紋樣技術主要源于數學模型的可視化，其中最重要的是分形算法，如迭代函數系統[1-2]、Julia集[3-4]、L系統[5-6]，均可產生新穎的、別具一格的圖案；其次是利用弱混沌系統[7]，包括準規則斑圖[8]、均勻隨機網[9]、哈密頓函數[10]等來生成紋樣圖案；其他生成圖案的方法還包括傅里葉變換[11]、參數化模型[12]等，這些方法用于紋樣創造(Creation)，可以產生新奇、有特色的圖案。但針對現有紋樣進行數字化改造(Innovation)，且在一定程度上保留原紋樣特征的新紋樣，未見系統性方法。紋樣改造和紋樣創造同樣重要，特別是對于經典傳統紋樣，有效地實施紋樣改造可為其注入新的生命力，是傳統文化保護和發揚的重要途徑。本文利用神經網絡對現有紋樣進行學習和改造的方法，通過將人工智能方法用于紡織紋樣的學習與重構，為紋樣的數字化創新開辟新的途徑。

1 研究方法

1.1 網絡模型

紡織紋樣可視為一個關系函數F，該函數描述紋樣中位置與顏色之間的關系，由式(1)表示：

C=F(P)

(1)

式中：P為紋樣在圖像中的位置；C為位置P處的顏色。

如果能掌握紋樣的關系函數F，就可以在各種條件下重建紋樣。關系函數F通常是非常復雜的，不能用簡單的數學公式描述，但可以通過人工神經網絡來學習和逼近。神經網絡結構見圖1。

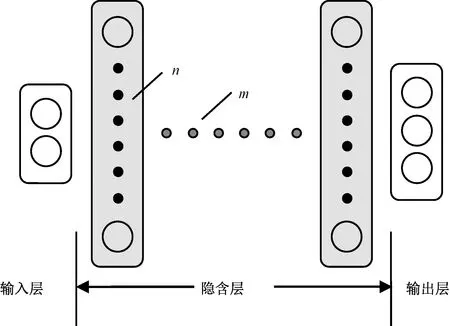
圖1 神經網絡結構

如圖1所示，該網絡包括一個輸入層、一個輸出層和若干隱含層。輸入層包含2個神經元，分別接受x、y坐標值輸入；輸出層包含3個神經元，分別輸出顏色r、g、b(紅、綠、藍)分量值；隱含層用來容納輸入、輸出層之間的關系模型F，其規模為n×m(n為每個隱含層所含神經元個數，m為隱含層數量)。由于輸入和輸出層神經元個數固定，隱含層的規模實際上決定了該網絡的規模。

該網絡的規模(即隱含層規模)可根據紋樣的復雜程度而定，復雜程度主要取決于紋樣中包含的顏色數目。如果網絡不能輸出令人滿意的結果，則可以擴大隱含層的規模。

另外，此網絡結構中的輸入和輸出值都應被標準化，以保證輸入/輸出數值落入范圍0～1內。坐標值x、y分別除以紋樣的寬度和高度進行標準化，顏色分量r、g、b則除以最大值255。

1.2 紋樣重構

紋樣學習就是訓練神經網絡用來逼近關系函數F。紋樣重構是指當網絡完整學習關系函數F后，利用它的輸出來重建紋樣。

紋樣圖像中的每個像素對應一個輸入樣本，該樣本即為對應像素的坐標值，其樣本標簽為對應像素的顏色值，如此1個紋樣構成1個訓練樣本集。紋樣圖像構成訓練樣本集見圖2。

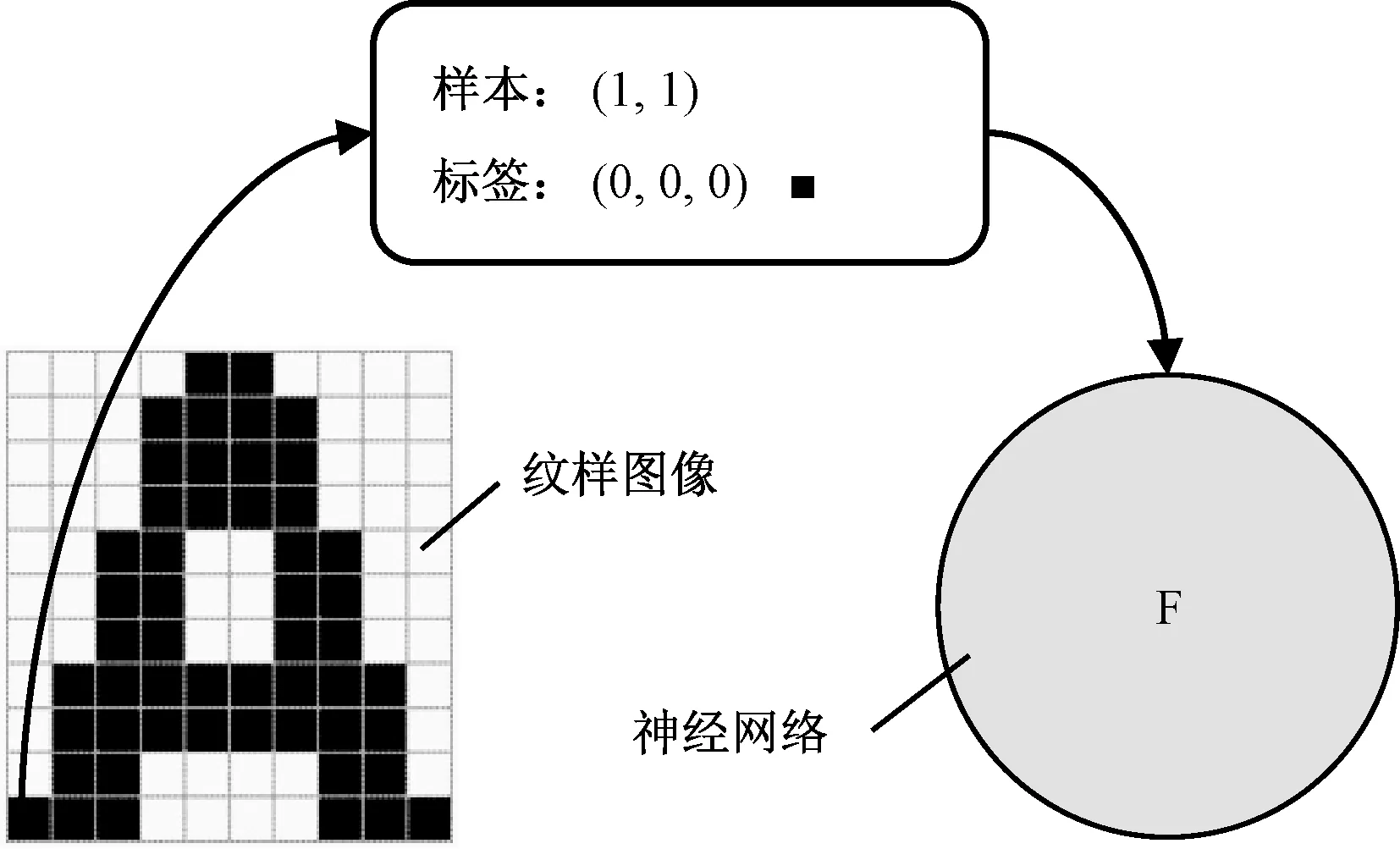
圖2 紋樣圖像構成訓練樣本集

使用該樣本集反復訓練網絡，采用反向回饋方法使網絡輸出與樣本標簽之間的誤差不斷減小，最終落入可接受的范圍內，即完成了紋樣學習。紋樣學習過程中的誤差變化見圖3。

圖3 紋樣學習過程中的誤差變化

由圖3可以看出，隨著訓練次數的增加，總體誤差不斷減小，逼近0。當誤差降低到一定程度，即可認為網絡完整學習了紋樣(即關系函數F)。一對坐標輸入，就會得到該坐標上的顏色輸出。紋樣重構見圖4。將這些顏色輸出重新置于對應的坐標上，便完成了紋樣重構。

圖4 紋樣重構

一般地，訓練次數越多，網絡輸出誤差越小，重構后的紋樣與原紋樣越接近。如果網絡輸出的誤差足夠小，該網絡稱為學習完善(Well-learnt)的網絡，如圖4(d)對應的網絡；否則稱為學習未完善(Poor-learnt)的網絡，如圖4(b)對應的網絡。這2種網絡之間沒有絕對的界限，但紋樣創新應該在學習完善的網絡上進行，以盡量保留原紋樣在造型或顏色上的一些特征。

1.3 紋樣改造

當神經網絡在一定程度上完整學習了關系函數F，可在網絡的輸入/輸出層上插入干擾函數，對輸入/輸出值進行調制，實現紋樣的改造和創新。干擾函數可以是任意函數，唯一的條件是其值域必須在0～1范圍內，以適應網絡模型對輸入/輸出值的要求。輸入干擾見圖5。

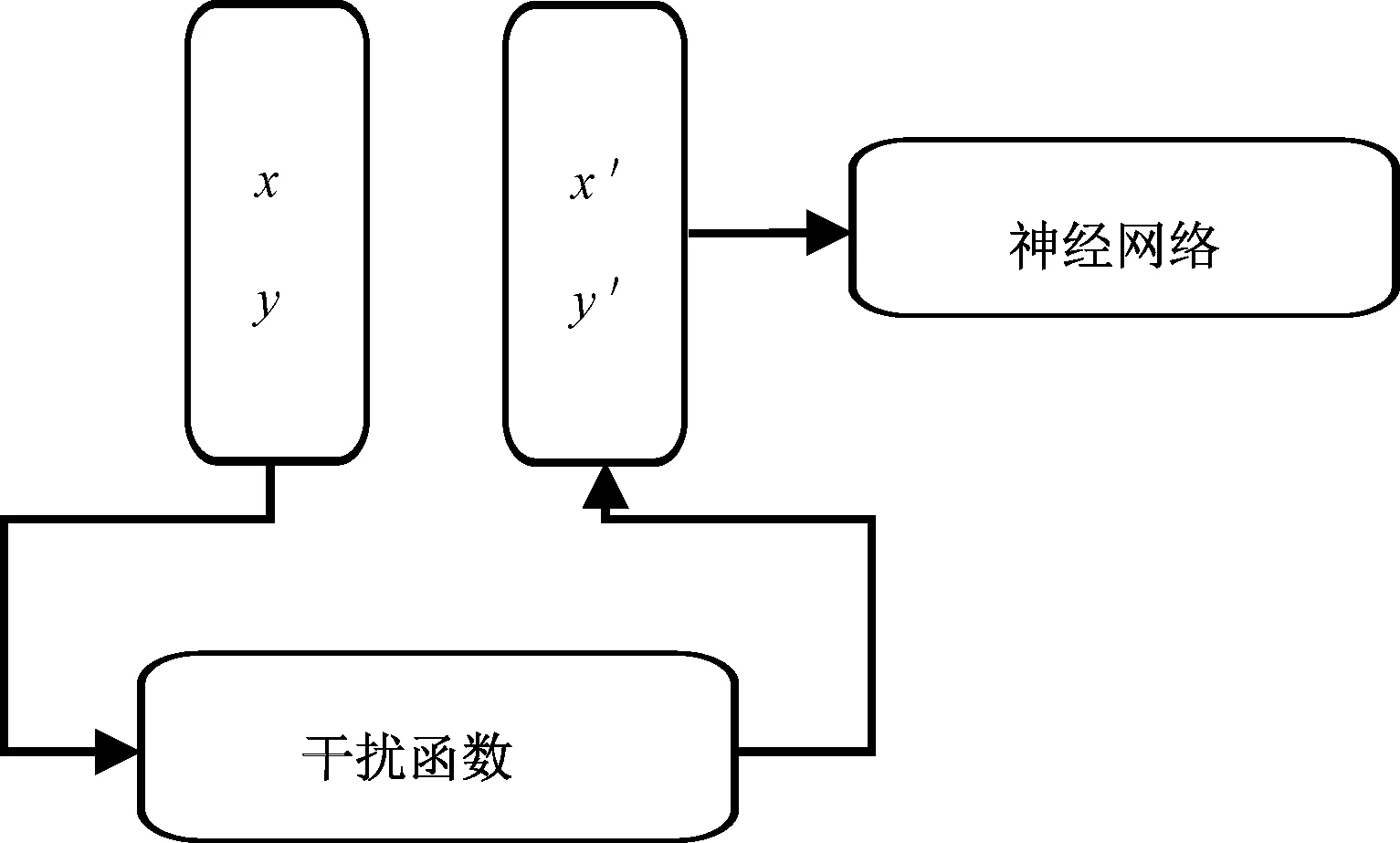
圖5 輸入干擾

在輸入層上，原輸入值x、y先經干擾函數處理并產生新的輸入值x′、y′，再將新的輸入值傳遞給神經網絡。因此，輸入干擾可定義為：

x′=Ix(x,y,r,g,b)

y′=Iy(x,y,r,g,b)

(2)

式中：Ix、Iy分別為原變量x、y上的干擾函數；x′、y′為相應干擾函數的結果變量；x、y、r、g、b為干擾函數中所涉及的變量，即參考變量。

通過輸入干擾進行紋樣改造，見圖6。

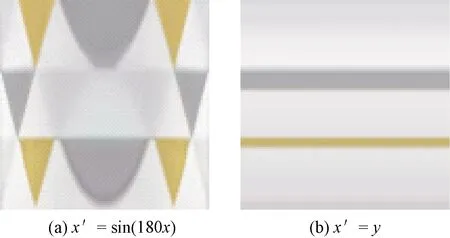
圖6 輸入干擾改造后的紋樣

在圖6(a)中，原變量x上的干擾函數利用正弦算子實施干擾，產生了具有對稱特征的新紋樣。該例中原變量y上的干擾函數實際為y′=y，如果某個干擾函數其結果變量等于原變量，則省略不寫。圖6(b)中，原變量x上的干擾函數將另一個原變量y賦予結果變量，實際上是對原紋樣的對角線特征進行橫向擴大。這2個紋樣都是在圖4(b)所對應的網絡(即學習完善的網絡)上施加干擾和輸出的。同理，可以在輸出層上插入干擾函數。原輸出值r、g、b經干擾函數處理并產生新的輸出值r′、g′、b′，再根據新的輸出值進行紋樣重構。輸出干擾見圖7。

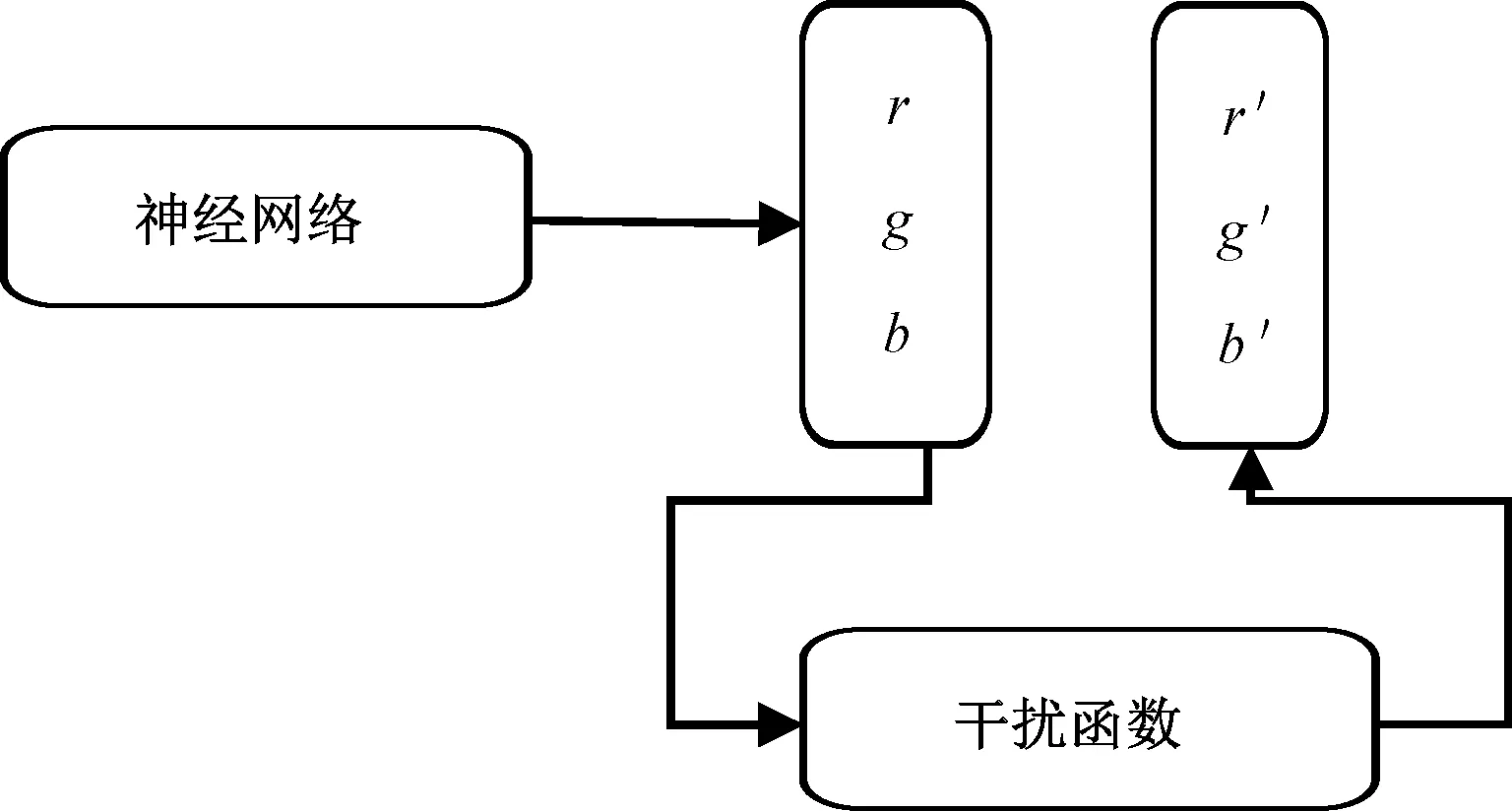
圖7 輸出干擾

輸出干擾可定義為：

r′=Ir(x,y,r,g,b)

g′=Ig(x,y,r,g,b)

b′=Ib(x,y,r,g,b)

(3)

式中Ir、Ig、Ib分別為原變量r、g、b上的干擾函數。

通過輸出干擾進行紋樣改造，見圖8。

圖8 輸出干擾改造后的紋樣

圖8(a)中，原變量r上的干擾函數以坐標x為其中一個參考變量實施干擾，對紋樣中的紅分量的橫向分布進行了調整。圖8(b)則同時對顏色變量r、g進行干擾，使得紋樣中的紅、綠分量的橫向和縱向分布發生了變化。可見，輸入干擾通過重塑造型進行紋樣改造和創新，而輸出干擾則是通過調整顏色分布的方式進行紋樣改造的。干擾函數中可以涉及的參考變量包括所有輸入和輸出變量。

2 結果與討論

2.1 網絡模型中的坐標形式

在本文研究中，將紋樣看作一個位置P與顏色C之間的關系模型，使用人工神經網絡學習該模型，從而能夠重構紋樣，以及進一步改造紋樣。如前所述，位置P由一對直角坐標(x,y)表示，但也可用其他形式表示，如極坐標(由極徑l和極角θ確定)。極坐標下的紋樣重構與創新見圖9。

圖9 極坐標下的紋樣重構與創新

圖9(a)為訓練8 000次后的輸出結果。圖9(b)中，原變量θ上的干擾函數以θ為參考變量，利用正弦算子實施干擾，產生的紋樣具有對角線對稱性質。圖9(c)中，原變量l上的干擾函數將參考變量θ直接賦予結果變量，其結果紋樣實際是原紋樣中所有數值滿足l=θ的點以左上角為中心的放射性擴展。圖9(d)是一個輸出干擾的例子，以θ為參考變量對顏色變量r實施干擾，使得結果紋樣中的紅分量在不同角度上的分布發生了變化。

同樣，顏色C除用RGB顏色(“紅/綠/藍”顏色)表達外，也可采用其他形式表達，如HSV顏色(“色調/飽和度/亮度”顏色)。HSV顏色下的紋樣重構與創新見圖10。

圖10 HSV顏色下的紋樣重構與創新

圖10 (a)是在HSV顏色下訓練8 000次后網絡輸出的結果。圖10 (b)是借助HSV顏色進行輸出干擾的結果，以坐標x、y為參考變量，利用if算子和正弦算子復合形式對顏色變量v實施干擾，使得結果紋樣出現了因明度變化引起的紋路。if算子的作用是條件選擇，它有3個參數，第1個參數是1個條件表達式，當該表達式成立時取第2個參數值，否則取第3個參數值。

總之，對圖1網絡結構，存在2種輸入形式(即直角坐標x、y輸入和極坐標l、θ輸入)和2種輸出形式(即RGB顏色輸出和HSV顏色輸出)。

2.2 紋樣重構的影響因素

如前所述，通過訓練可使神經網絡完整學習紋樣關系模型，然后將網絡輸出置于對應的位置上，實現紋樣重構。試驗發現，極坐標形式下紋樣學習過程與直角坐標形式類似，即總體誤差隨著訓練次數的增加而下降并逼近0。圖9(a)和圖4(d)同為訓練8 000次后的輸出結果，其圖像質量基本相當。

顏色表達方面，在神經網絡中使用HSV顏色進行學習和重構，其效率和精度不如使用RGB顏色，圖10 (a)與圖4(d)相比精度較低。數字圖形設備(如電腦顯示器)基本上都使用RGB顏色，因此神經網絡中的HSV數據需要經過2次轉換，第1次是構造訓練樣本時將數字設備上的RGB數據轉換成HSV數據，第2次是在網絡輸出后要將HSV數據轉換成RGB顏色以便在顯示器上繪制。由于RGB顏色與HSV顏色并不一一對應，2次轉換導致的精度損失使得HSV顏色下的紋樣重構不能令人十分滿意。

此外，紋樣重構的結果與訓練次數和網絡規模有關。訓練次數對紋樣重構的影響已由圖3、4顯示。給定訓練次數t=8 000，不同網絡規模下的紋樣重構見圖11。其中時間耗費(s)除以最大值進行標準化處理。

圖11 不同網絡規模下的紋樣重構

由圖11可以看出，在同樣的訓練次數下，網絡規模越大，逼近能力越強，輸出紋樣與原紋樣越接近，但時間耗費也越多。過大的規模可能不是必要的，圖11(c)(d)顯示的重構紋樣差異非常微小幾乎可以忽略，但耗費時間有顯著不同。經驗表明，如果網絡輸出長時間內不能達到訓練目標，則應擴大網絡規模。擴大網絡規模不會引起所謂“過擬合”問題，因為該網絡并不需要應用到新的紋樣上，即它不需要適應新的樣本。

2.3 紋樣創新

如前所述，通過在網絡的輸入/輸出點上插入干擾函數，對位置/顏色值進行調制，可實現紋樣創新。對位置輸入的干擾帶來紋樣造型的改造，而對顏色輸出的干擾帶來紋樣色彩分布的改造。紋樣改造能夠產生非常豐富、新奇的圖案，再結合簡單的鏡像處理，即可得到四方連續的紡織紋樣。鏡像處理見如圖12。

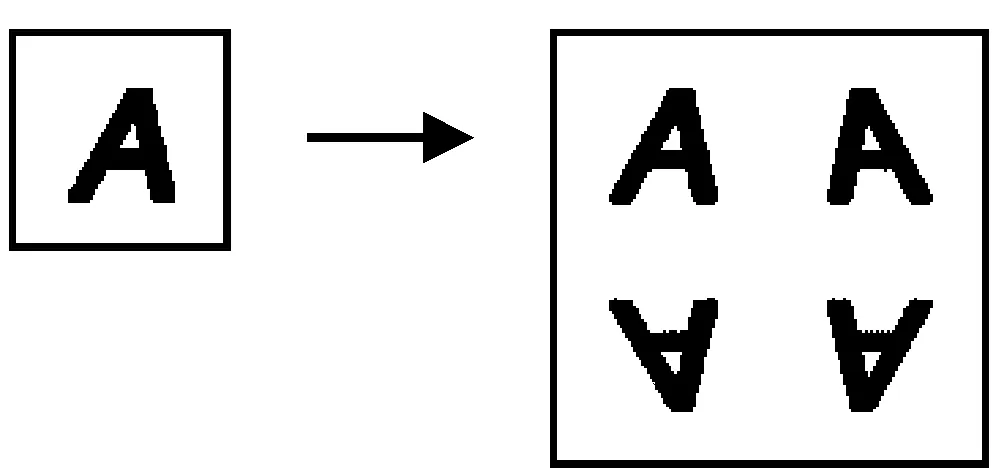
圖12 鏡像處理

這種利用干擾函數實施的紋樣改造不是隨機、不可控的，其是有規律、可控的。本文總結幾種典型的紋樣改造方式及其對應的干擾函數。

2.3.1 條紋化

條紋化是指提取原紋樣中的直線或曲線特征構成新的條紋紋樣，這是通過輸入干擾實現的，圖6(b)、圖9(c)都是條紋化改造的例子。條紋化改造的關鍵是，某個輸入變量上的干擾函數以另一個輸入變量為唯一參考變量。條紋化改造效果見圖13。生成的紋樣已經過鏡像處理。

圖13 條紋化改造效果

圖13(a)、(b)中，輸入變量y上的干擾函數以另一個輸入變量x為唯一參考變量。圖13(c)、(d)中，輸入變量θ上的干擾函數以另一個輸入變量l為唯一參數。它們的干擾函數中都使用了冪指數算子或三角算子。冪指數算子和三角算子是干擾函數中的基本算子，它們能保證計算結果在0～1范圍內，此外三角算子的周期性還能帶來圖案上的對稱和重復。

2.3.2 扭曲化

在輸入干擾中，如果某個輸入變量上的干擾函數同時依賴2個原輸入變量，結果紋樣呈現扭曲效果，扭曲化改造效果見圖14。

圖14 扭曲化改造效果

圖14(a)中，輸入變量l上的干擾函數被指定為2個原變量l、θ的復合運算形式，其中指數上的三角運算單元的絕對取值是為了保證其介于0～1內，從而結果變量也介于0～1之間。圖14(d)中對原變量x、y分別實施干擾，干擾函數都以2個原變量為參考變量。

2.3.3 沙 化

沙化是借助rand算子實現的一種隨機效果，rand算子的作用是生成0～1之間的均勻分布的隨機數。沙化改造效果見圖15。

圖15 沙化改造效果

圖15(a)是在圖14(a)所示紋樣基礎上進行的沙化處理，使用rand算子對輸入變量θ實施干擾。圖15(b)是對圖13(b)所示紋樣進行沙化，使用if算子有選擇地對紋樣中的某些區域進行處理。

2.3.4 疊 印

在輸出干擾中，如果干擾函數以位置變量(x、y、l、θ)為參數變量，并且使用高頻三角算子進行調制，可以得到帶有彩色紋路的疊印圖案。與條紋化處理得到的紋路不同，這種紋路是色彩因子分布規律性變化帶來的。疊印改造效果見圖16。其三角算子的頻率越高，紋路越細，如圖16(a)、(b)所示。疊印處理的另一個特點是，處理灰度紋樣也能產生豐富的彩色疊印效果，圖16(d)是對圖16(c)所示灰度紋樣進行疊印處理的結果。

圖16 疊印改造效果

3 結 論

本文研究將紡織紋樣視為位置和顏色之間的關系函數。使用人工神經網絡學習該關系函數，利用網絡輸出重構紋樣，可取得與原紋樣非常接近的效果。通過在網絡輸入輸出層上設置干擾函數來進行紋樣改造和創新，可獲得非常豐富的紋樣效果。

①在網絡模型方面，采用1個輸入層(2個輸入點)、1個輸出層(3個輸出點)和若干隱含層的反向回饋網絡結構，通過調節隱含層的規模可控制網絡容量以適應不同的紋樣關系函數。

②在紋樣重構方面，從紋樣像素構造網絡輸入樣本集，通過反復訓練將誤差降低到可接受的范圍內，將網絡的顏色輸出重新置于對應位置上實現紋樣重構。重構的精度受網絡規模、訓練時間和樣本集顏色模式的影響，網絡規模越大、訓練時間越長，重構精度越高；在樣本集中采用RGB顏色比采用其他顏色(如HSV)獲得的重構精度高。

③在紋樣創新方面，通過在網絡輸入輸出層上設置干擾函數，對輸入輸出量進行調制來實現紋樣改造和創新。在輸入層上設置干擾函數，對輸入位置進行調制，可實現紋樣造型的改造。在輸出層上設置干擾函數，對輸出顏色進行調制，可實現紋樣顏色分布的改造。通過在干擾函數中包含相應的結果變量、原變量、參考變量及某些特殊算子，可以實現條紋化、扭曲化、沙化和疊印4種主要的紋樣改造創新效果。

總之，基于人工神經網絡的紋樣重構與創新方法，可為紡織紋樣的數字化創新提供一條便捷的途徑。