考慮潮汐影響的連續泊位分配策略

徐亞偉 王志明 李蕓

摘要：針對潮汐影響下船舶進出港調度中的連續泊位分配策略優化需求，考慮潮汐影響下的船舶進出港時段、船舶靠離泊安全流速、泊位類型與船型相匹配等多因素約束，根據先來先服務原則，構建混合整數規劃模型，并采用改進粒子群優化（particle swarm optimization，PSO）算法進行求解。算例結果給出每艘船的靠泊位置和進出港順序安排，并通過與標準PSO算法求解的調度方案進行對比，驗證改進PSO算法的有效性。研究成果可為實際碼頭泊位分配決策提供參考。

關鍵詞： 連續泊位分配; 粒子群優化（PSO）算法; 潮汐影響; 先來先服務原則

中圖分類號： U691+.3 ? ?文獻標志碼： A

Abstract： In view of the demand of the continuous berth allocation strategy optimization in the scheduling of ships entering and leaving a port under the influence of tide， considering the constraints such as the time window of ships entering and leaving a port under the influence of tide， the safe flow rate of ship berthing and unberthing， and the matching of the berth type and the ship type， according to the first-come first-served principle， a mixed integer programming model is constructed， and an improved particle swarm optimization （PSO） algorithm is used to solve the model. The results of the example show the berthing positions and the sequence of entering and leaving a port of ships， and the results are compared with the scheduling scheme solved by the standard PSO algorithm to verify the effectiveness of the improved PSO algorithm. The research results can provide reference for the actual berth allocation decision-making.

Key words： continuous berth allocation; particle swarm optimization （PSO） algorithm; influence of tide; first-come first-served principle

0 引 言

在航海實踐中，若船舶提前進港則可能沒有泊位靠泊，船舶必須在港口內等待，這不僅對船舶安全不利，而且也有礙港口內其他船舶安全航行;若船舶延遲進港，則港口與船舶的等待時間必將延長，勢必造成港口服務效率下降。隨著港口吞吐量的增加及船舶數量的增多，合理的船舶進出港安排和泊位分配已經成為港口急需解決的問題。

近年來，由于全球港口吞吐量的增加，船舶進出港調度與泊位分配問題引起了學術界廣泛關注。在船舶進出港調度研究方面：張新宇等[1]為提高雙向通航港口的船舶調度效率，使用多目標遺傳算法獲取最佳調度方案;BIERWIRTH等[2]針對船舶調度問題進行了詳細的屬性分類研究。在離散泊位研究方面：IMAI等[3-4]首先提出了離散型泊位分配模型，然后在此基礎上提出了考慮船舶優先權的泊位分配模型;韓笑樂等[5]考慮了具有不同服務優先級別的船舶動態到達情形，以船舶在港總時間與加權延遲時間之和最小為目標，設計結合禁忌深度搜索算法與模擬退火算法的混合算法求解;TING等[6]考慮船舶動態到達情況下的泊位分配問題，以服務總時間最短為目標函數，設計粒子群優化（particle swarm optimization，PSO）算法求解;ZHEN等[7]考慮潮汐時間窗口和航道通行能力約束，建立泊位分配和岸橋分配的綜合優化模型，以等待和延誤總時間最短為目標函數，提出基于列生成算法的求解方法來求解該模型的最優解;鄭紅星等[8]針對考慮潮汐影響的泊位分配與船舶集成調度問題，構建了混合整數規劃模型，并設計了改進禁忌搜索算法求解。在連續泊位研究方面：童珊[9]針對考慮船舶優先權的泊位分配問題，以提高集裝箱船在港口的靠泊效率為目標，建立混合整數規劃模型，并利用遺傳算法進行求解。樂美龍等[10]在研究泊位和岸橋分配時，側重考慮泊位偏好和服務優先權兩大因素，以最小化所有船舶的在港總時間為目標建模并利用遺傳算法求解;SHEIKHOLESLAMI等[11]在研究集裝箱碼頭的動態泊位分配問題時，考慮了船舶優先權以及潮汐對錨地到碼頭的航道的影響，采用遺傳算法結合模式搜索算法求解該問題;DU等[12]考慮了潮汐和船舶虛擬到達策略，以船舶離港延誤總時間最短為目標建模，用CPLEX進行求解;張雯鈺等[13]考慮了公平措施，以船舶在港時間最短和集裝箱碼頭懲罰成本最小為優化目標建模，并設計了模擬退火算法進行求解。

綜上所述，現有關于船舶進出港調度和泊位分配的研究雖力求更加符合實際調度過程，但缺少考慮潮汐對船舶泊位分配的影響的深入研究，相關成果與滿足港口實際調度需求還有一定差距。本文針對潮汐影響下的船舶進出港次序與泊位分配問題，以船舶到港至離港的總時間最短為目標，總體上滿足先來先服務的原則，側重分析在安全流速下船舶靠離泊時段和船舶乘潮進出港的時間窗口，并采用改進PSO算法確定船舶進出港次序和泊位分配方案。

1 參數定義及泊位分配問題描述

1.1 參數定義

V表示到港船舶集合，i，j∈V;Vin表示需乘潮進港的船舶集合;Vout表示需乘潮出港的船舶集合;G表示港口泊位集合，b∈G;T表示時間序列集合，t∈T;K表示潮汐周期集合，k=1，2，…，K。ai為船i到港時刻;Touti為船i離開港口時刻;Xi表示船i靠泊的位置;Li表示船i的長度;Ti，w1表示船i等待進港時間;Ti，w2表示船i完成裝卸作業后等待離泊時間;Tbi表示船i準備靠泊時刻;T fi表示船i泊位作業完成時刻;Ci表示船i在碼頭的作業時間;Tini表示船i進港時刻;C表示船舶通過航道的時間;LB表示碼頭泊位的長度;TDi表示船i準備離泊時刻;TEDi表示預計船i離開泊位的時刻;M表示一個足夠大的正數;Sb表示泊位b的類型，其值1、2分別表示普通船泊位、需乘潮進出港船泊位;Hi表示船i的類型，其值1、2分別表示普通船、需乘潮進出港船;Eini表示船i的預計進港時刻;[Wi，k，B1，Wi，k，B3]表示需乘潮船i在第k次潮汐周期中可以乘潮進出港的時間窗口;[Wi，k，d2，Wi，k，d3]和[Wi，k，d4，Wi，k+1，d1]表示船i在第k次潮汐周期中可以靠離泊的時間窗口;[Wi，k，d1，Wi，k，d2]和[Wi，k，d3，Wi，k，d4]表示船i在第k次潮汐周期中不可以靠離泊的時間窗口。XBij，若船i與船j的泊位沒有重疊，則為1，否則為0;XTij，若船i與船j的靠泊時間在時間軸上沒有重疊，則為1，否則為0;Xi，t，b，若在t時間船i靠泊在泊位b上，則為1，否則為0;Ui，b，若船i延遲進港，則為1，否則為0;Zi，b，若船i延遲出港，則為1，否則為0;δini，k，若需乘潮船i的進港時刻在第k次潮汐周期中可以乘潮進港的時間窗口內，則為1，否則為0;δouti，k，若需乘潮船i的離泊時刻在第k次潮汐周期中可以乘潮出港的時間窗口內，則為1，否則為0。

1.2 泊位分配問題描述

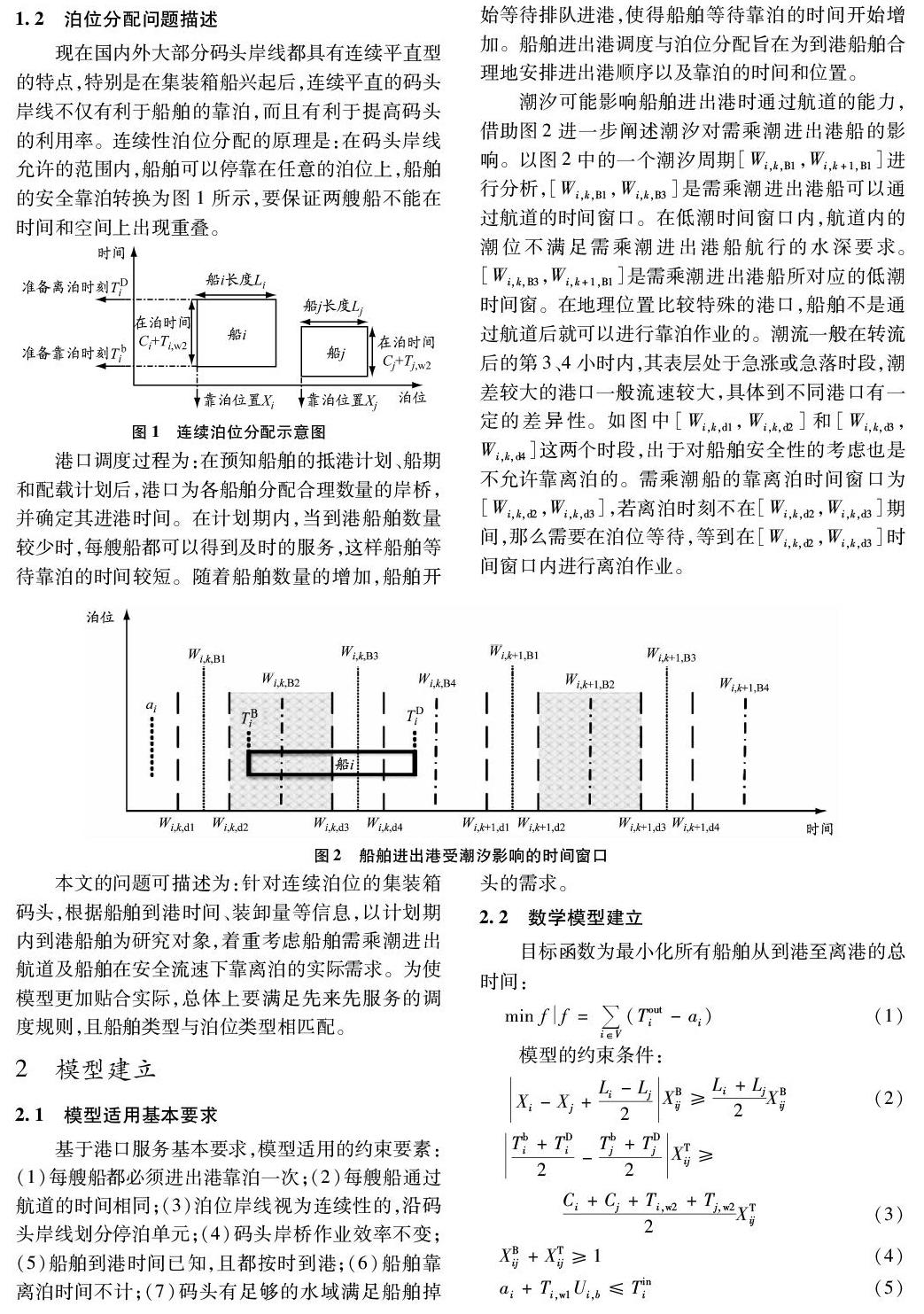
現在國內外大部分碼頭岸線都具有連續平直型的特點，特別是在集裝箱船興起后，連續平直的碼頭岸線不僅有利于船舶的靠泊，而且有利于提高碼頭的利用率。連續性泊位分配的原理是：在碼頭岸線允許的范圍內，船舶可以停靠在任意的泊位上，船舶的安全靠泊轉換為圖1所示，要保證兩艘船不能在時間和空間上出現重疊。

港口調度過程為：在預知船舶的抵港計劃、船期和配載計劃后，港口為各船舶分配合理數量的岸橋， 并確定其進港時間。在計劃期內，當到港船舶數量較少時，每艘船都可以得到及時的服務，這樣船舶等待靠泊的時間較短。隨著船舶數量的增加，船舶開始等待排隊進港，使得船舶等待靠泊的時間開始增加。船舶進出港調度與泊位分配旨在為到港船舶合理地安排進出港順序以及靠泊的時間和位置。

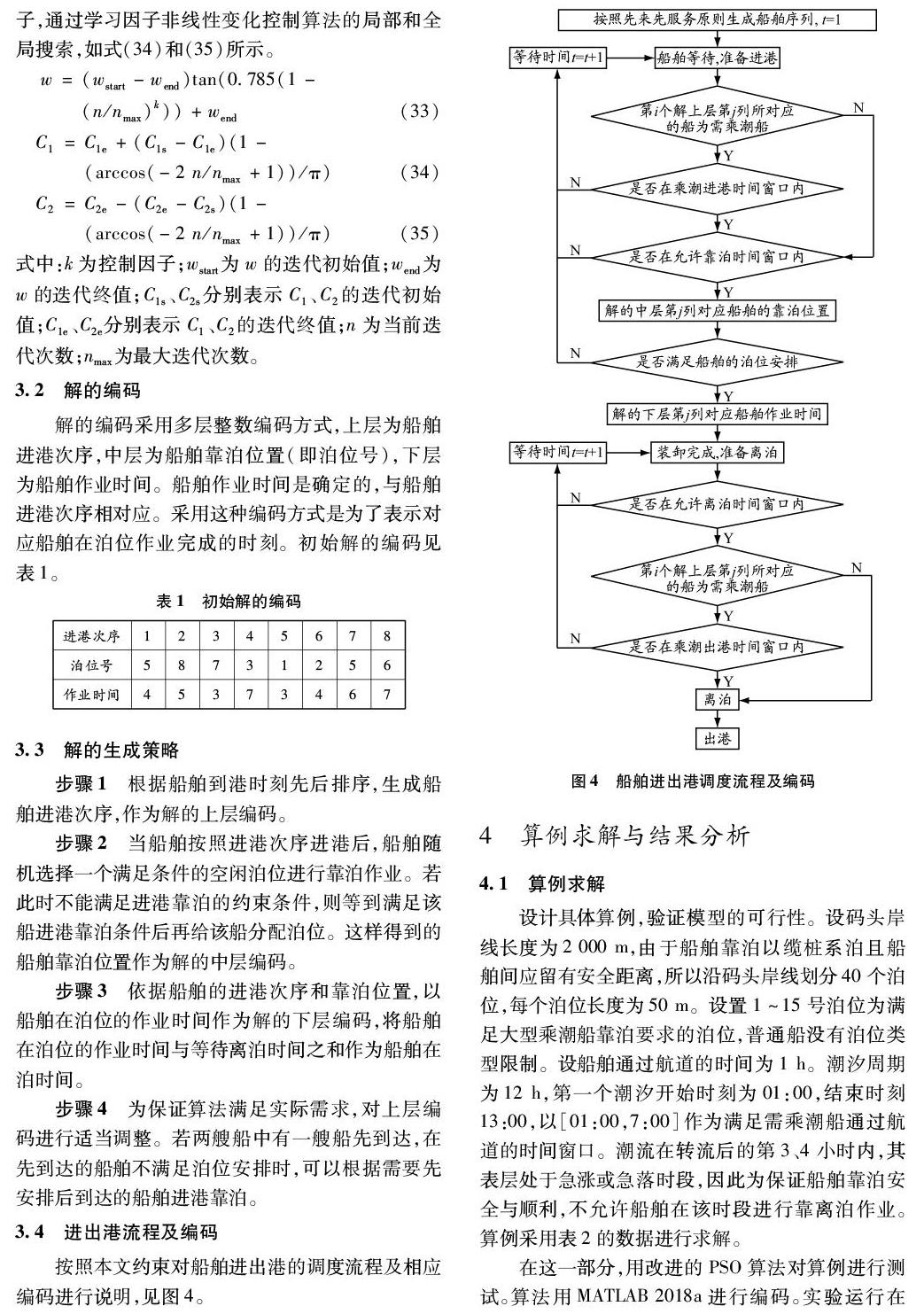
潮汐可能影響船舶進出港時通過航道的能力，借助圖2進一步闡述潮汐對需乘潮進出港船的影響。以圖2中的一個潮汐周期[Wi，k，B1，Wi，k+1，B1]進行分析，[Wi，k，B1，Wi，k，B3]是需乘潮進出港船可以通過航道的時間窗口。在低潮時間窗口內，航道內的潮位不滿足需乘潮進出港船航行的水深要求。[Wi，k，B3，Wi，k+1，B1]是需乘潮進出港船所對應的低潮時間窗。在地理位置比較特殊的港口，船舶不是通過航道后就可以進行靠泊作業的。潮流一般在轉流后的第3、4小時內，其表層處于急漲或急落時段，潮差較大的港口一般流速較大，具體到不同港口有一定的差異性。如圖中[Wi，k，d1，Wi，k，d2]和[Wi，k，d3，Wi，k，d4]這兩個時段，出于對船舶安全性的考慮也是不允許靠離泊的。需乘潮船的靠離泊時間窗口為[Wi，k，d2，Wi，k，d3]，若離泊時刻不在[Wi，k，d2，Wi，k，d3]期間，那么需要在泊位等待，等到在[Wi，k，d2，Wi，k，d3]時間窗口內進行離泊作業。

本文的問題可描述為：針對連續泊位的集裝箱碼頭，根據船舶到港時間、裝卸量等信息，以計劃期內到港船舶為研究對象，著重考慮船舶需乘潮進出航道及船舶在安全流速下靠離泊的實際需求。為使模型更加貼合實際，總體上要滿足先來先服務的調度規則，且船舶類型與泊位類型相匹配。

2 模型建立

2.1 模型適用基本要求

基于港口服務基本要求，模型適用的約束要素：（1）每艘船都必須進出港靠泊一次;（2）每艘船通過航道的時間相同;（3）泊位岸線視為連續性的，沿碼頭岸線劃分停泊單元;（4）碼頭岸橋作業效率不變;（5）船舶到港時間已知，且都按時到港;（6）船舶靠離泊時間不計;（7）碼頭有足夠的水域滿足船舶掉頭的需求。

2.2 數學模型建立

3.3 解的生成策略

步驟1 根據船舶到港時刻先后排序，生成船舶進港次序，作為解的上層編碼。

步驟2 當船舶按照進港次序進港后，船舶隨機選擇一個滿足條件的空閑泊位進行靠泊作業。若此時不能滿足進港靠泊的約束條件，則等到滿足該船進港靠泊條件后再給該船分配泊位。這樣得到的船舶靠泊位置作為解的中層編碼。

步驟3 依據船舶的進港次序和靠泊位置，以船舶在泊位的作業時間作為解的下層編碼，將船舶在泊位的作業時間與等待離泊時間之和作為船舶在泊時間。

步驟4 為保證算法滿足實際需求，對上層編碼進行適當調整。若兩艘船中有一艘船先到達，在先到達的船舶不滿足泊位安排時，可以根據需要先安排后到達的船舶進港靠泊。

3.4 進出港流程及編碼

按照本文約束對船舶進出港的調度流程及相應編碼進行說明，見圖4。

4 算例求解與結果分析

4.1 算例求解

設計具體算例，驗證模型的可行性。設碼頭岸線長度為2 000 m，由于船舶靠泊以纜樁系泊且船舶間應留有安全距離，所以沿碼頭岸線劃分40個泊位，每個泊位長度為50 m。設置1～15號泊位為滿足大型乘潮船靠泊要求的泊位，普通船沒有泊位類型限制。設船舶通過航道的時間為1 h。潮汐周期為12 h，第一個潮汐開始時刻為01：00，結束時刻13：00，以[01：00，7：00]作為滿足需乘潮船通過航道的時間窗口。潮流在轉流后的第3、4小時內，其表層處于急漲或急落時段，因此為保證船舶靠泊安全與順利，不允許船舶在該時段進行靠離泊作業。算例采用表2的數據進行求解。

在這一部分，用改進的PSO算法對算例進行測試。算法用MATLAB 2018a進行編碼。實驗運行在2.3 GHz Intel Core（TM） i5-8300H CPU和16 GB內存的計算機上。改進PSO算法的參數設置為：粒子數N=600;最大迭代次數n=4 000;慣性權重wstart=0.9，wend=0.1;學習因子C1s=2.5，C2s=0.5，C1e=0.5，C2e=2.5;k=0.4。在按照實際需求先來先服務的基礎上，最終運行得到船舶進出港調度方案，見表3。

改進PSO算法求解的泊位分配方案見圖5。由圖5可以看出：需乘潮船進港都有延遲，這主要是因為這種船需要在可以乘潮進出港的時間窗口內進出港，并且船舶類型需要滿足碼頭泊位類型的要求：普通船3、9、10、20進港靠泊都有延遲，這是因為普通船需要在安全流速下靠泊;船舶到達安排總體上滿足先來先服務的原則，圖中船舶都在安全時間窗口內靠離泊，以及在合適的時間窗口內進出港。根據該模型得出的結果，可以有序地安排船舶進出港及選擇相應的泊位。改進PSO算法求解出的目標函數總時間比標準PSO算法求解得出的小，說明采用改進PSO算法能提高解的質量。

潮汐因素影響船舶的進出港次序及船舶靠離泊的時間安排，從而影響后續船舶的泊位分配，因此，在港口服務中需要著重關注潮汐因素對泊位分配的影響。本文所用的模型具有以下特點：考慮先來先服務原則，保證該模型在更大程度上滿足航海實踐需求，遵循到港船舶服務公平性的原則;更加全面地考慮到實際船舶需要在安全流速下靠離泊，以及在合適的潮汐時間段進出港;考慮不同水深情況下泊位類型的情況，以滿足航海實務中船舶停靠的實際泊位需要。本文所得到的結果對于安排船舶進出港及泊位分配有一定的參考價值。

4.2 改進PSO算法有效性驗證

為驗證所采用的改進PSO算法在搜索性能上的增強，用標準PSO算法對同樣的實驗進行對比，參數設置為：粒子數N=600;最大迭代次數n=4 000;慣性權重w=0.8;學習因子C1=1.5，C2=1.5。具體的調度方案見圖6。圖7是算法求解過程：當改進PSO算法迭代約2 600次時，目標函數值收斂于252 h;當標準PSO算法迭代到約2 400次時，目標函數值收斂于256 h。

為增加實驗結果的可靠性，增加幾組實驗來體現算法改進前后的效果。在其他參數相同的情況下，選取其他20艘船，沿碼頭岸線分布40個泊位，最大迭代次數n=1 000，算法求解過程見圖8。選取其他25艘船，沿碼頭岸線分布50個泊位，最大迭代次數n=5 000，算法求解過程見圖9。

以上一系列數據仿真結果證明，所采用改進PSO算法的求解質量優于標準PSO算法。在改進PSO算法和標準PSO算法求解過程中，隨著迭代次數不斷增加，目標函數值均不斷優化，但是改進PSO算法能在提高算法收斂性的同時能夠有效避免陷入局部最優的情況，算法搜索能力更強。因此，上述分析符合預想的情況。

5 結束語

為滿足大型船舶順利進出港及安全靠泊的實際需求，本文在前人研究的基礎上考慮潮汐影響下的泊位分配策略。相較于以往的研究，著重分析了在安全流速下船舶靠離泊時段和需乘潮船進出港的時間窗口，建立了以船舶從到港至離港總時間最短為目標的函數，采用改進PSO算法求解該模型。算例結果顯示，所提出的船舶泊位分配模型能有效地安排船舶進出港及泊位分配，改進PSO算法求解出的方案優于標準PSO算法求解出的方案。

從本文的研究結果可知，船舶進出港次序與泊位分配受到潮汐因素的影響，因此，在港口服務中需要著重關注潮汐因素對泊位分配的影響。就提高該模型的實際應用價值而言，對多因素綜合約束類問題的理論研究還需通過實踐優化，才能最終轉化成便于用戶操作的實用工具。

參考文獻：

[1] 張新宇， 郭子堅， 王金濤， 等. 基于航道與泊位資源協調調度的船舶交通優化[J]. 中國航海， 2015， 38（3）： 33-36.

[2] BIERWIRTH C， MEISEL F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals[J]. European Journal of Operational Research， 2015， 244（3）： 675-689. DOI： 10.1016/j.ejor.2014.12.030.

[3] IMAI A， NISHIMURA E， PAPADIMITRIOU S. The dynamic berth allocation problem for a container port[J]. Transportation Research Part B， 2001， 35（4）： 401-417. DOI： 10.1016/s0191-2615（99）00057-0.

[4] IMAI A， NISHIMURA E， PAPADIMITRIOU S. Berth allocation with service priority[J]. Transportation Research Part B， 2003， 35（7）： 437-457. DOI： 10.1016/s0191-2615（02）00023-1.

[5] 韓笑樂， 陸志強， 奚立峰. 具有服務優先級別的動態離散泊位調度優化[J]. 上海交通大學學報， 2009， 43（6）： 902-905. DOI： 10.16183/j.cnki.jsjtu.2009.06.011.

[6] TING C J， WU K C， CHOU Hao. Particle swarm optimization algorithm for the berth allocation problem[J]. Expert Systems with Applications， 2014， 41（4）： 1543-1550. DOI： 10.1016/j.eswa.2013.08.051.

[7] ZHEN Lu， LIANG Zhe， ZHUGE Dan， et al. Daily berth planning in a tidal port with channel flow control[J]. Transportation Research Part B Methodological， 2017， 106： 193-217. DOI： 10.1016/j.trb.2017.10.008.

[8] 鄭紅星， 吳云強， 邵思楊， 等. 考慮潮汐影響的泊位分配與船舶調度集成優化[J]. 信息與控制， 2020， 49（1）： 95-103. DOI： 10.13976/j.cnki.xk.2020.9091.

[9] 童珊. 基于船舶優先權的集裝箱港口泊位分配問題[J]. 交通運輸工程與信息學報， 2012， 10（1）： 105-110.

[10] 樂美龍， 劉秀玲. 基于泊位偏好與服務優先級的泊位和岸橋分配[J]. 遼寧工程技術大學學報（自然科學版）， 2013， 32（5）： 709-712.

[11] SHEIKHOLESLAMI A， IIATI G， KOBARI M. The continuous dynamic berth allocation problem at a marine container terminal with tidal constraints in the access channel[J]. International Journal of Civil Engineering， 2014， 12（3）： 344-353.

[12] DU Yuquan， CHEN Qiushuang， LAM J S L， et al. Modeling the impacts of tides and the virtual arrival policy in berth allocation[J]. Transportation Science， 2015， 49（4）： 939-956. DOI： 10.1287/trsc.2014.0568.

[13] 張雯鈺， 郝楊楊. 基于船舶作業優先權的靠泊計劃仿真優化研究[J]. 計算機仿真， 2020， 37（6）： 130-135.

[14] BABAZADEH A， SHAHBANDI M G， SEYEDALIZADEH-GANJI S R， et al. A PSO algorithm for continuous berth allocation problem[J]. International Journal of Shipping & Transport Logistics， 2015， 7（4）： 479-493. DOI： 10.1504/IJSTL.2015.069687.

[15] 李麗， 牛奔. 粒子群優化算法[M]. 北京： 冶金工業出版社， 2009： 44-59.

[16] 陳水利， 蔡國榕， 郭文忠， 等. PSO算法加速因子的非線性策略研究[J]. 長江大學學報（自科版）理工卷， 2007， 4（4）： 1-4.

（編輯 賈裙平）