基于卡爾曼濾波的兩輪平衡姿態檢測系統設計
賈 勇,陳曉飛
(新疆工程學院 信息工程學院,烏魯木齊 830023)
0 引言
兩輪平衡系統是一種自然穩定性差、非線性、欠驅動的系統,以兩輪平衡車為例,若想維持車體的穩定性和平衡度,務必確保車身的重心和車輪的重心一直保持在同一個軸線上面[1]。在車體的平衡控制階段,姿態傳感器需要把檢測所得的車體傾角信號發送到控制器當中,通過相關計算得到控制量對左右電機進行驅動的控制力矩,進而對兩輪平衡車的右輪的運動速度與方向進行調節,能夠讓兩輪平衡車車輪沿著傾斜的方向運動,進而達到讓兩輪平衡車恢復到直立狀態的目的[2]。然而,傳統的互補濾波融合算法下的檢測控制借助的是傳統的慣性傳感器,因為慣性傳感器自身具備的固有特性,導致檢測過程中,傳感器會被溫度和噪聲等因素進行干擾,使得傳感器發生某種程度的偏移現象,這就會使得車體姿態檢測過程很難對真實的姿態角度進行檢測,所以在兩輪平衡姿態的檢測當中,需要借助多傳感器信號的信息融合,對最佳姿態角度進行檢測[3]。在得到傳感器檢測出的相關數據之后,傳統方式是利用互補濾波算法對傳感器檢測的數據進行融合,然而這種算法的置信度的設置比較固定,在動態的條件下,融合效果差,融合精度低,進而導致檢測效果差。
基于此提出以多傳感器為基礎的多傳感器信息融合算法的兩輪平衡姿態檢測系統,即為基于卡爾曼濾波的兩輪平衡姿態檢測系統。兩輪平衡系統被廣泛應用在軍事、航天、科研工作等諸多領域,具有非常廣闊的發展前景,具有很大的應用價值與實際價值,是當今社會著重關注的熱點之一所以基于卡爾曼濾波的兩輪平衡姿態檢測系統的設計具有十分重要的意義。
1 硬件系統結構設計
硬件部分的總體構成框架包括加速度計、上位機顯示器、姿態采集傳感器、PC通信、電動驅動、換向信息部分、主控芯片CPU、電源模塊,微控制器模塊,左右輪機等[4]。姿態檢測系統的核心是數字信號處理器,負責對相關數據信息進行獲取,分析處理與傳遞。主要構成部件有陀螺儀,姿態檢測系統的主體硬件結構設計如圖1所示。

圖1 硬件結構設計
針對上述內容,對硬件各個部分展開詳細分析。
1.1 姿態傳感器的設計
兩輪平衡系統的本質是一個不穩定的多變量系統,姿態檢測系統需要借助SCA610-CA1H1G型號姿態傳感器,姿態傳感器是以MEMS技術為基礎的,高性能的三維運動姿態測量系統[5]。姿態傳感器包含著諸多的組件,比如三軸陀螺儀、三輪加速計等一系列的運動傳感器。姿態傳感器的工作原理是借助內嵌的低功耗的ARM處理器進行相關的處理,進而能夠獲取到進行過溫度補償的三維姿態和方位的相關信息數據[6]。之后再借助以四元數為基礎的三維算法設計與特定的數據信息等技術四元數、歐拉角等用于對三維姿態方位數據信息進行表示與輸出。姿態傳感器的應用范圍很廣泛,比如航模、無人機、機械云平臺、虛擬現實、以及兩輪平衡系統等諸多方面[7]。
基于卡爾曼濾波的兩輪平衡姿態檢測系統設計當中,利用加速度計與陀螺儀借助整合型的6軸運動處理組件模塊形成新型的姿態傳感器電路,對比于傳統方式的傳感器的方式,剔除了加速計和陀螺儀間的軸差間形成的誤差數據,此外,在一定程度上也節省了很大的空間姿態傳感器的減速帶感測范圍是±250°/sec(dps)、±500°/sec(dps)、±1 000°/sec(dps)。
姿態傳感器的主要構成結構如圖2所示。

圖2 姿態傳感器結構圖
由圖2可知,使用能夠對快速、慢速等動作進行精確、較高的感應。姿態傳感器具備諸多特性,主要特性如下:
1)具有多數據輸出接口,比如串口式接口,SPI接口,12C接口等。
2)功耗很低,通過實際測量得出約為17 mA。
3)姿態傳感器是復合型濾波和數據的融合,利用了捷聯式慣導技術。
4)三維姿態方位數據的輸出是全角度的,并且沒有盲區的。
5)開機啟動快,進入穩定狀態系統消耗時間短,大約是0.1 s。
6)數據輸出率值很高,最大上限為500 Hz。
7)功耗很低,通過實際測量得出約為17 mA。
8)具備可選擇的多種數據輸出模式,比如歐拉角,旋轉矩陣,四元數等[8]。
1.2 硬件控制電路設計
電源的穩定性在整個系統中占據非常重要的地位,基于卡爾曼濾波的兩輪平衡姿態檢測系統利用的是獨立電源的設計,電源的組成部分的主體是多個相互獨立的電源共同執行供電任務,通過這種設計能夠很大程度上減弱因為每個模塊瞬時通過過大電流造成的整個系統的穩定性被破壞的問題。
電路中電源的設計指標如下所示:
1)對于直流減速電機供電的電源最適宜選取36 V電源。
2)對于有關外電路的供電最佳選擇5 V的電源。
3)系統的總電源由36 V鉛酸電池充當,把3個12 V 12 AH的鉛酸電池利用串聯在一起,保證能夠提供36 V的電能能源,經過DC/DC轉換之后,向各個用電模塊供電。
1.3 主控芯片CPU設計
主控芯片Pentium II/III/4系列CPU被稱作系統的“心臟”,因此它在整個系統中的地位非常高。CPU控制芯片能夠將系統的需要與相關可利用的資源進行重新組合、整合、分配、規劃利用[9]。CPU是一種能夠編程化的特殊性質的集成電路,CPU是可編程化的一種集成電路,屬于處理器的種類之一,它可以把所有組成元件執行小型化的處理、壓縮等存儲在電路之中,它是一種集成電路,能夠在一端或者是多端對編碼指令進行接收,運行該指令下達的內容,并將它的狀態信息進行描述和對外輸出,一系列的指令信息可以集中存儲在系統內部,別名半導體中央處理器,即CPU,屬于微型計算機的重要組成部件之一。微處理器的構件通常安裝在一個單片或者是同一個構件內部,然而卻不能保證一定分布在同一芯片上,可以分布在不同芯片上。
2 兩輪姿態檢測軟件設計
2.1 基于卡爾曼濾波去噪
由于硬件采集到的數據是包含噪聲的數據,因此,需將采集數據作為樣本數據,采用卡爾曼濾波法去除噪聲[10],去噪流程如圖3所示。
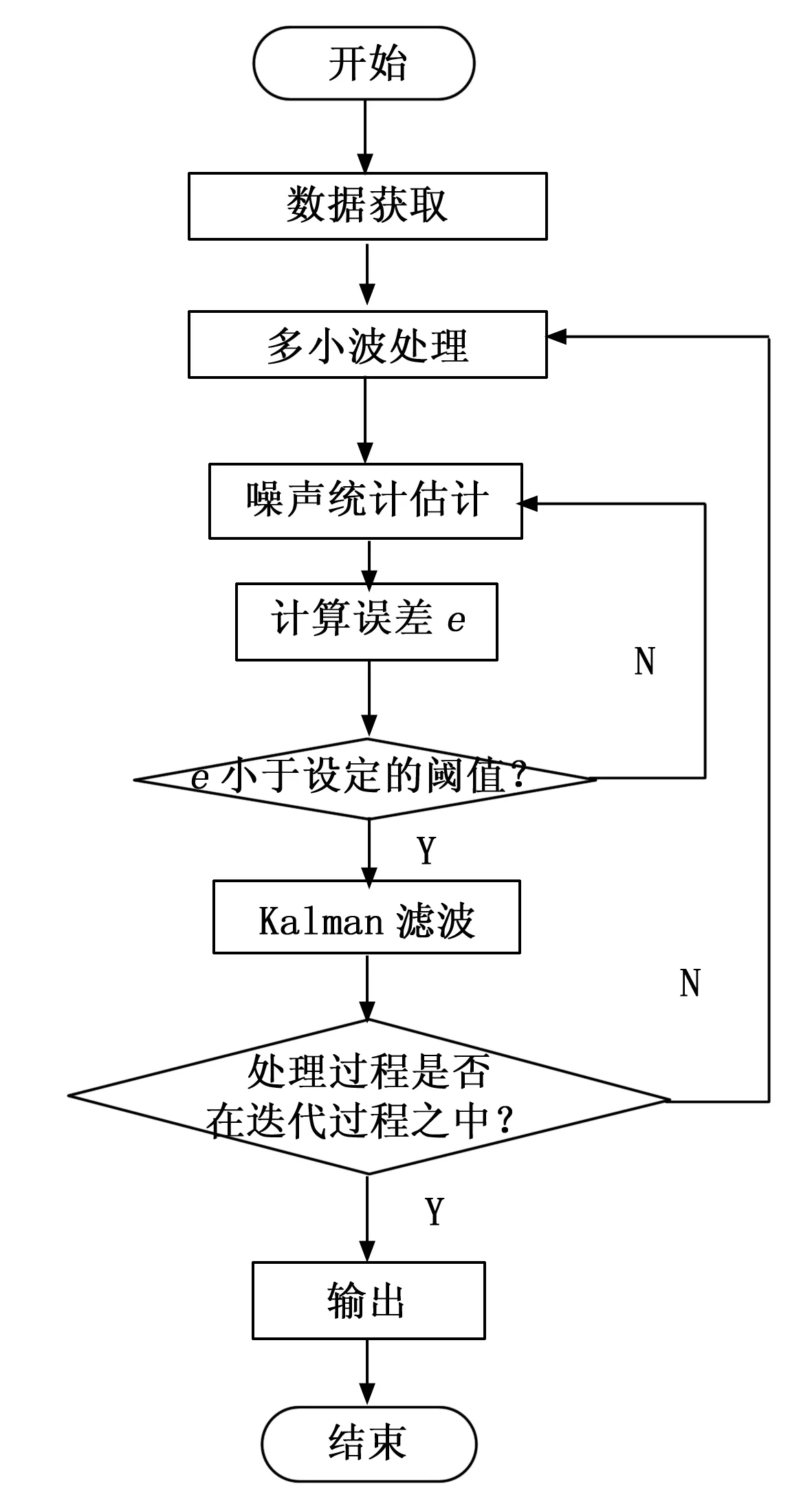
圖3 基于卡爾曼濾波去噪流程
由圖3可知,在獲取測量角速度信息后,對告饒信號初步消噪,并使用噪聲估計量統計噪聲值大小,利用卡爾曼濾波,判斷整個估計過程是否在迭代中進行,如果是,則直接輸出去噪后的數據,否則,重復檢測,直到滿足條件為止,為兩輪平衡姿態檢測提供數據支持[11]。
2.2 兩輪平衡姿態檢測流程設計
對于姿態檢測系統,只利用陀螺儀或者是加速儀都不能夠獲得到具有價值性并且精確度較高的信息,來確保系統的整體平衡度[12],兩輪平衡姿態檢測流程設計如下所示:
步驟一:根據上述卡爾曼濾波檢測流程剔除噪聲數據后,設定兩輪工作參數;
步驟二:利用狀態更新方程依據目前的系統運行情況以及噪聲的方差對下一個狀態的將運行狀況進行相關的估計與測量。
步驟三:將檢測的結果當作濾波器的輸入信息數據,借助狀態更新獲得先驗狀態的預估計狀態,進行一些列的狀態估計操作。
步驟四:依據下一時刻系統預計誤差,估計前一時刻系統預計誤差,獲取卡爾曼增益。
步驟五:構建誤差修正模型,由三軸陀螺儀和重力加速度計組成的系統,需將地理坐標系上重力加速度通過四元數轉旋轉矩陣轉移到當前設備坐標系上處理,設四元數方程為:
E=w(a0+a1+a2+a3)
(1)

Qbc=
(2)
地理坐標系重力向量為g,經過旋轉后,得到的重力向量到設備坐標系為:
gb=Qbc·g=

(3)
對測量數值進行歸一化處理,可得到無量綱標量。
步驟六:為了提高檢測精度,需更新四元數,使用定時采樣三階逼近法,計算公式為:
(4)
公式(4)中,?為陀螺儀在采樣周期內角增量,將該計算結果代入四元數方程中可確定兩輪平衡姿態旋轉方向,由此完成姿態檢測。
3 實驗研究
為了驗證基于卡爾曼濾波的兩輪平衡姿態檢測系統設計合理性,進行實驗驗證分析。
3.1 實驗背景與參數設置
以互補濾波檢測系統作為實驗對比方法,以兩輪平衡小車為實驗對象,對兩種算法的數據曲線效果,進而反映姿態檢測系統的準確度。車體運動簡化模型如圖4所示。

圖4 車體運動簡化模型
實驗的設置環境背景是,將兩輪平衡車的車體傾角在人為控制的前提下,把角度值由0°,逐漸上升到了25°左右之后,又逐漸下降到0的過程。在這個過程當中,兩輪平衡車的車體的運動狀態是由靜止變成加速狀態,之后變成慢慢減速至速度為0的靜止狀態。實驗的基本前提是需要保證在整個實驗的過程當中,加速度傳感器需要保持相對平穩狀態,盡力控制對加速傳感器造成的“抖動”狀態,并且要將它的加速度控制在一個小范圍當中,進行相關實驗。加速度計直接測出的數據曲線的效果比較精確,將它作為空白對照組,作為參照和卡爾曼濾波器與互補濾波器下的實驗結果進行對照分析,進而得出相關的結論。
3.2 實驗結果與分析
3.2.1 0~15 dB噪聲環境下
在0~15 dB噪聲環境下,分別采用互補濾波設計的檢測系統和基于卡爾曼濾波方法設計的檢測系統對旋轉角度檢測進行對比分析,結果如表1所示。
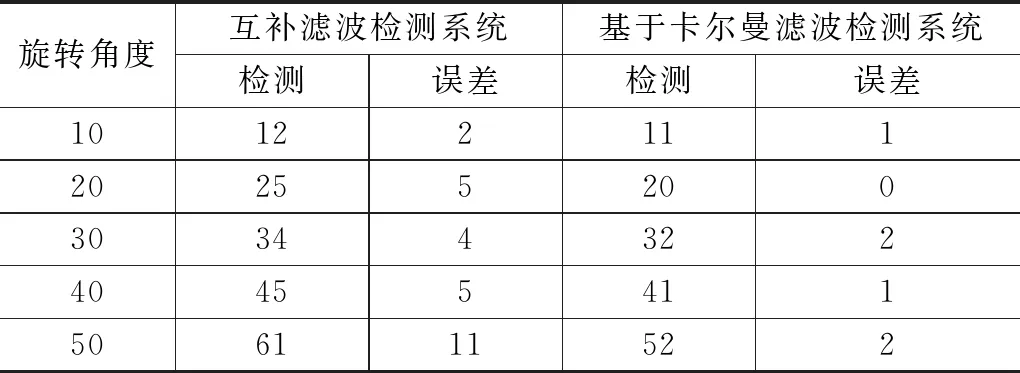
表1 0~15 dB噪聲環境下兩種系統旋轉角度對比分析 (°)
由表1可知,使用互補濾波設計的檢測系統在0~15 dB噪聲環境下,檢測誤差最大為11°,最小為2°;而使用基于卡爾曼濾波方法設計的檢測系統在0~15 dB噪聲環境下,檢測誤差最大為2°,最小為0°,由此可知,使用基于卡爾曼濾波方法設計的檢測系統檢測誤差較小。
3.2.2 15~30 dB噪聲環境下
15~30 dB噪聲環境下,同樣使用這兩種系統對旋轉角度檢測進行對比分析,結果如表2所示。
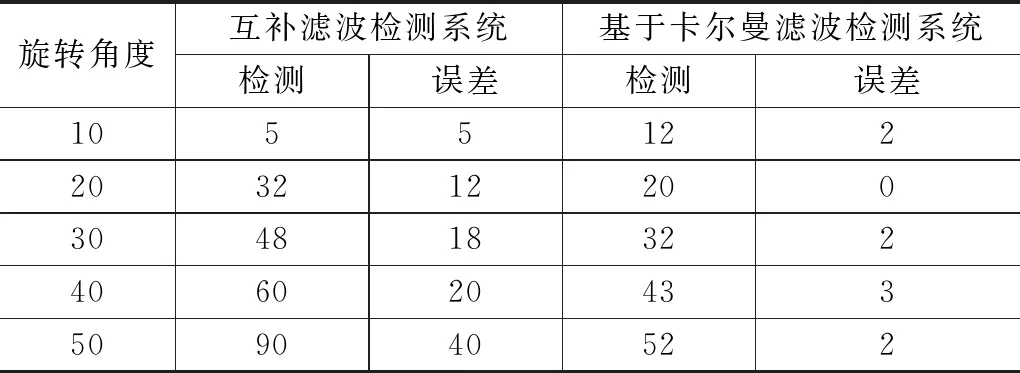
表2 15~30 dB噪聲環境下兩種系統旋轉角度對比分析 (°)
由表2可知,使用互補濾波設計的檢測系統在15~30 dB噪聲環境下,檢測誤差最大為40°,最小為5°;而使用基于卡爾曼濾波方法設計的檢測系統在0~15 dB噪聲環境下,檢測誤差最大為3°,最小為0°,由此可知,使用基于卡爾曼濾波方法設計的檢測系統檢測誤差較小。
結合上述對比情況,再次將兩種系統的檢測精準度進行對比分析,結果如圖5所示。

圖5 兩種系統檢測精準度對比分析
由圖5可知,在0~15 dB噪聲環境下,使用基于卡爾曼濾波方法設計的檢測系統,在旋轉角度為10°時,檢測精準度為85%。在旋轉角度為50°時,檢測精準度最高為92%;在15~30 dB噪聲環境下,使用基于卡爾曼濾波方法設計的檢測系統,在旋轉角度為10°時,檢測精準度為84.5%,在旋轉角度為50°時,檢測精準度最高為90%。
而采用互補濾波系統的檢測系統在0~15 dB噪聲環境下,旋轉角度為10°時,檢測精準度為18%。在旋轉角度為50°時,檢測精準度最高為51%;在15~30 dB噪聲環境下,使用基于卡爾曼濾波方法設計的檢測系統,在旋轉角度為10°時,檢測精準度為8%,在旋轉角度為50°時,檢測精準度最高為31%。
綜上所述,基于卡爾曼濾波的兩輪平衡姿態檢測系統檢測精準度較高。
4 結束語
基于卡爾曼濾波的兩輪平衡姿態檢測系統能夠精準檢測出兩輪平衡姿態旋轉方向,實驗結果表明卡爾曼濾波下的角度擬合曲線與多傳感器融合測量的加速度計測出角度曲線的角度差值比傳統的互補濾波小,擬合效果更好,說明檢測精度較高通過卡爾曼濾波有效地修正了零位誤差,減小了震動干擾的影響,同時實現了對動態傾角的平滑濾波。除此之外,這種方法與傳統的互補濾波方法相比,能夠更加容易借助嵌入式系統達成,提高姿態檢測性能的同時也方便了對兩輪自平衡車學習控制算法的深入研究。

