VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
Tao TAN (譚濤) Tao CHEN (陳陶) Lijun WU(吳黎君)? Yuhong SHENG (盛玉紅)
College of Mathematics and System Science, Xinjiang University, Urumqi, Xinjiang 830046, China E-mail : tantao.math@hotmail.com; chentao 1994@hotmail.com; xjmath@xju.edu.cn; sheng-yh12@mails.tsinghua.edu.cn

under the VaR and TVaR risk measures,and showed that two-layer reinsurance is always the optimal reinsurance policy under both the VaR and TVaR risk measures.From the perspective of an insurer,Cai et al.[5]studied the optimal reinsurance treaty by means of an approximation approach by minimizing the VaR and CTE of the insurer’s liability,where the admissible ceded loss functions were assumed to be the increasing convex functions.This method is quite complicated,as pointed out by Chi and Tan[9].For any increasing convex ceded loss functionI(x),Chi and Tan[9]demonstrated that it can be rewritten as

for some constantc∈[0,1]and a probability measureνdefined on[0,∞],where(x)+:=max{x,0}.This representation can greatly simplify the proof of Cai et al.[5].Later,Huang and Yu[17]further studied the optimal safety loading of the reinsurance premium principle based on the work of Cai et al.[5].However,it is well known that the insurer and the reinsurer have a conflict interest in a few of reinsurance contracts.Therefore,a natural and interesting question arises:with the admissible class of increasing convex ceded loss functions,and from the reinsurer’s perspective,what is the corresponding optimal reinsurance treaty?
In the present article,we will investigate the above-mentioned question.Namely,by employing the increasing convex functions as the admissible ceded loss functions,and from the reinsurer’s perspective,we study the optimal reinsurance treaty by minimizing the VaR of the reinsurer’s liability under the distortion premium principle.When the distortion premium principle is specified to the expected value premium principle,we study the optimal reinsurance treaty by minimizing the CTE of the reinsurer’s liability.The optimal reinsurance treaties are provided.It turns out that the obtained optimal reinsurance treaties are quite different from those of Cai et al.[5].The present study can be considered as a complement of that of Cai et al.[5].
The rest of this article is organized as follows:in Section 2,we briefly introduce the preliminaries.In Section 3,the optimal reinsurance design is studied under VaR,and the optimal reinsurance treaty is obtained in general.In Section 4,the optimal reinsurance design is studied under CTE,and the optimal reinsurance treaty is obtained in general.Finally,a conclusion of this article is provided.
2 Preliminaries
Let a non-negative random variableXwith positive and finite expectationE[X]be the loss initially faced by an insurer.We denote by X all the non-negative random variables with positive and finite expectations.We denote byFX(x)the distribution function ofX,and bySX(x):=1?FX(x)the survival function ofX.Assume thatXhas a continuous strictly increasing distribution function on(0,+∞)with a possible jump at 0.Furthermore,we assume that the survival functionSX(x)is differentiable with a negative derivative;that is,(x)<0 for allx>0.We denote by I the class of ceded loss functions,which consists of all increasing convex functionsI(x)defined on[0,∞)satisfying 0≤I(x)≤xforx≥0,but excludingI(x)≡0.
Under a reinsurance contract,the insurer cedes part of its loss,sayI(X)with 0≤I(X)≤X,to a reinsurer,and thus the retained loss of the insurer isRI(X):=X?I(X),where the functionI(x),satisfying 0≤I(x)≤x,is called the ceded loss function,and the functionRI(x):=x?I(x)is called the retained loss function.In exchange,the insurer agrees to pay a reinsurance premium to the reinsurer.Denote byπI(X)the reinsurance premium which corresponds to the ceded lossI(X).By definition,a distortion functionr:[0,1]→[0,1]is a non-decreasing function such thatr(0)=0,r(1)=1.The inverse ofris defined byr?1(x):=inf{y:r(y)≥x}.Corresponding to a distortion functionr,the distortion premium principleπis defined by

forX∈X,whereρ>0 is the safety loading.
Ifr(x)=x,then the distortion premium principle recovers the expected value principle.Throughout this article,we assume that the distortion functionr(x)has at least finitely many discontinuous points,withx=0 being a continuous point ofr.
Upon the issuing of a reinsurance contract,the total risk exposure of the reinsurer is

Note that(i)is from(15)of Dhaene et al.[16].(ii)follows from(i).(iii)is from Porth,Tand and Weng[23].
Next,we state the following lemma,the proof of which can be found in Lemma 2.1 of Cheung and Lo[14]:

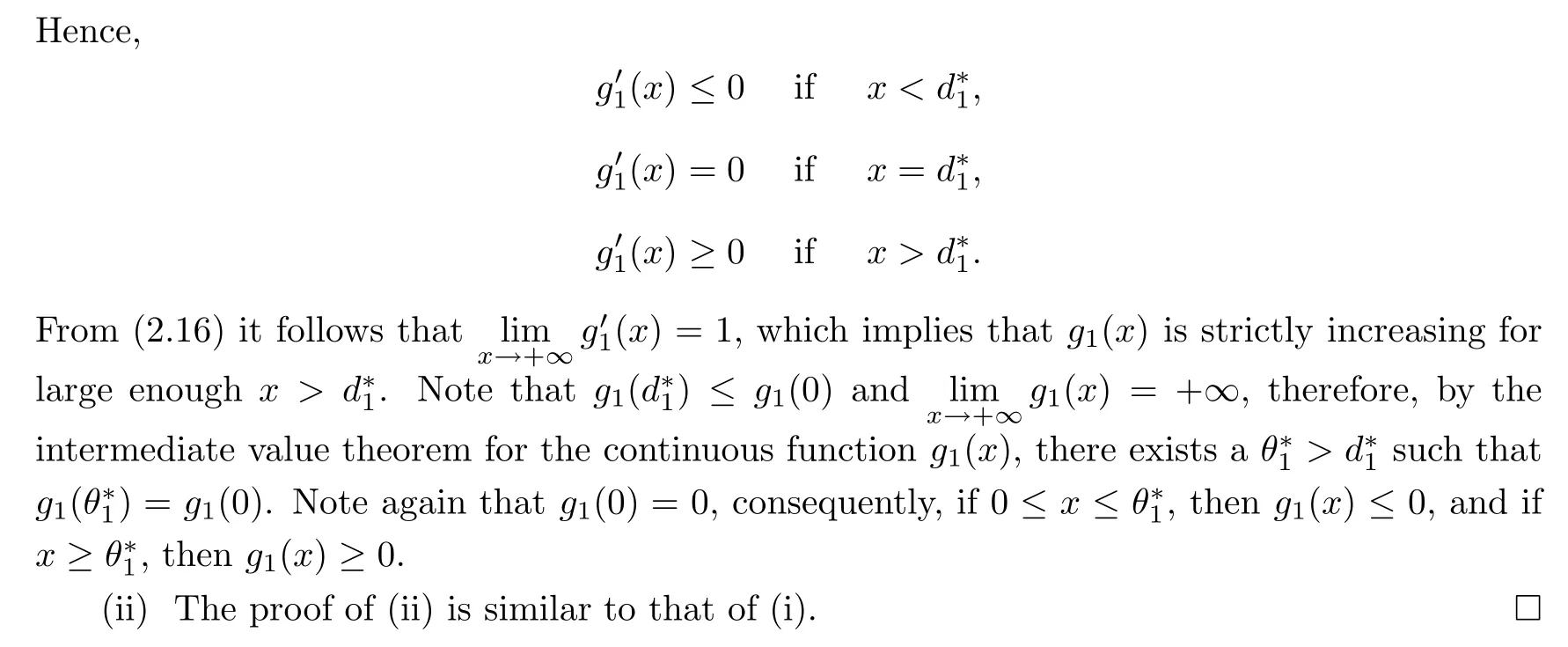
3 VaR-based Optimal Reinsurance
In this section,we will derive the optimal solution to model(2.9)under the admissible ceded loss functions.We begin this section with the following lemma,which is from Chi and Tan([10],Lemma 3.1):



Remark 3.3Theorem 3.2 shows that from the reinsurer’s perspective,the optimal reinsurance treaty is different from that of the insurer;see[5]for the optimal reinsurance treaty from the insurer’s perspective.These different ideas as to what constitutes the optimal treaty reflects the conflict interest between the insurer and the reinsurer in a reinsurance contract.How to balance both the insurer’s and the reinsurer’s interests in a reinsurance contract is an interesting issue,and this will be the subject of further work.
In the special case where the distortion functionr(x)=x,x≥0,


4 CTE-based Optimal Reinsurance
In this section,we will derive the optimal solution to model(2.10)under the admissible ceded loss functions with the expectation premium principle.Recall that from(2.7)and(2.11),we obtain



In this case,we need only to setνwith support on{0,VaRα(X)}.If CTEα(X)>u2(0)=u2(VaRα(X)),we setc=0,so the corresponding optimal ceded loss function becomesI?(x)=0.If CTEα(X)=u2(0)=u2(VaRα(X)),then the corresponding optimal ceded loss function becomesI?(x)=cxfor somec∈[0,1]orI?(x)=c(x?VaRα(X))+for somec∈[0,1].If CTEα(X) If CTEα(X)>u2(VaRα(X)),we setν(VaRα(X))=1 andc=0,so the corresponding optimal ceded loss function becomesI?(x)=0.If CTEα(X)=u2(VaRα(X)),then the corresponding optimal ceded loss function becomesI?(x)=c(x?VaRα(X))+for somec∈[0,1].If CTEα(X) (II)Assuming thatα<ρ?, In this case,we setν(∞)=1,and the corresponding optimal ceded loss function becomesI?(x)=0. Theorem 4.1 is proved. Remark 4.2Theorem 4.1 shows that from the reinsurer’s perspective,the optimal reinsurance treaty is different from that of the insurer;see[5]for the optimal reinsurance treaty from the insurer’s perspective. Remark 4.3Under the assumption that the class of increasing convex functions is the admissible ceded loss functions,Huang and Yin[18]studied the optimal reinsurance treaty by an approximation approach under the distortion risk measure and the distortion premium principle from the perspectives of an insurer and a reinsurer.This method is quite complicated,as pointed out by Chi and Tan[9].For any increasing convex ceded loss functionI(x),Chi and Tan[9]demonstrated that it can be rewritten as In this article,we have used this representation of an increasing convex function to derive the optimal reinsurance treaty,and this method is different from the one used by Huang and Yin[18]. In this article,we have studied two optimal reinsurance models from the reinsurer’s perspective.Under the assumption that the admissible ceded loss functions consist of all increasing convex functions,when the reinsurance premium principle is calculated by a general distortion premium principle,we obtained the optimal reinsurance treaties by minimizing the VaR of the reinsurer’s total risk exposure.When the reinsurance premium principle is calculated by a general expected value premium principle,we obtained the optimal reinsurance treaties by minimizing the CTE of the reinsurer’s total risk exposure.It turns out that the optimal reinsurance treaty for the reinsurer is quite different from that of the insurer.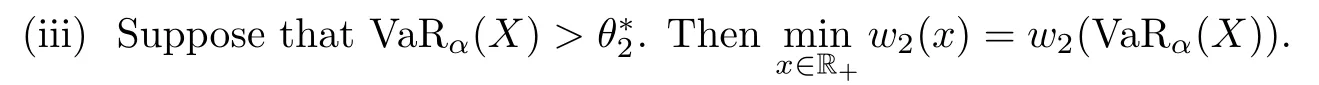
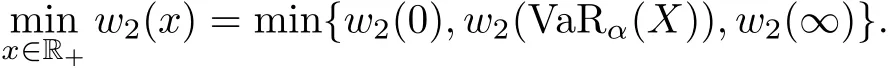

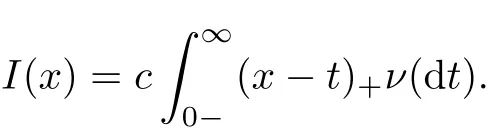
5 Conclusion
 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
