基于投影的不確定型多屬性群決策的Dice相似度法

周文坤

（上海大學 管理學院，上海 200444）

0 引言

隨著科學技術的發展和信息技術的推進，決策問題日益成為社會與經濟生活的重要內容之一，并且呈現出決策參與者越來越多的群體化特征，以及表達決策的信息具有很大的不確定性。由于客觀事物的復雜性和不確定性以及人類思維的模糊性，在群體決策過程中決策者往往不能明確地給出屬性的權重信息，而給出的屬性值是區間數形式的非實數值。對于這類不確定型群體決策問題的研究具有重要的理論意義和實際應用價值，因為它符合人類思維具有的不確定性特征，對決策者的思維過程刻畫比較符合實際狀況，因而它描述的決策過程也就更加細致與真實。在不確定型多屬性群體決策中，群體決策者面對決策屬性時往往使用沒有明確偏好信息的區間數作為評價值，首先需要對區間數信息進行集結處理，然后選擇最優備選方案或進行方案排序［1］。目前，不確定型多屬性群體決策在管理科學、決策理論、系統工程、運籌學等學科研究中都占據十分重要的地位，已經廣泛地應用于投資決策、項目評價、方案優選、工廠選址、經濟效益綜合評價等諸多領域，具有重要的理論價值和應用前景。根據國內外相關文獻，把投影模型引入群體決策中用于集成決策者的屬性權重獲得群體屬性權重，并使用Dice模型作為集成決策信息的研究沒有報道［2，3］，大多數文獻都采用TOPSIS法［4～6］和可能度法［7～20］。本文針對屬性權重和決策者權重均為未知的不確定型多屬性群體決策問題，利用規范化處理后的屬性值，建立各決策者的理想解權重模型并用投影模型集成求得群體屬性權重，同時還計算各決策者的權重，進而集成得到群體的綜合決策矩陣，并計算各方案與群體理想解的Dice相似度，再根據各方案與群體理想解的Dice相似度值大小對各方案進行優劣排序。最后，通過實例對該算法進行詳細驗證，結果表明本文提出算法的有效性和實用性。

1 不確定型多屬性群體決策模型

1.1 數據規范化

1.2 各決策者的屬性權重

1.3 確定決策者的權重

1.4 群體決策的Dice相似度

若方案與群體正理想解的相似度值越大，則對應的方案就越優。因此，以相似度值作為決策標準，相似度值越大則對應的方案就越好，相似度值越小則對應的方案就越差，從而可以確定群體對方案的決策排序。

2 不確定型多屬性群體決策的Dice算法

不確定型多屬性群體決策的Dice算法，首先分別計算各決策者的理想解權重，再集結成系統屬性權重，同時計算各決策者的權重，可以通過系統屬性權重和決策者權重集結成群體綜合決策矩陣，然后利用群體正理想解作為參照物，計算各方案與群體理想解的Dice相似度，并以Dice相似度值作為排序依據，確定各方案的優劣排序。因此，其詳細步驟如下：

步驟1對不確定型多屬性群決策，決策者El給出決策矩陣并按照式（3）和（4）對決策矩陣進行規范化處理，得到決策者El的規范化矩陣

步驟2根據式（9）計算屬性權重向量W*，并歸一化后得到系統屬性權重向量W**；

步驟3按式（14）計算決策者El的權重λl（l∈Q）；

步驟4由系統屬性權重向量W**和決策者El的權重λl（l∈Q），得到群體綜合決策矩陣

步驟5計算備選方案Xi與群體正理想解X*的Dice相似度；

步驟6根據Dice相似度由大到小對方案進行排序，相似度越大則對應的方案就越優。

因此，不確定型多屬性群決策的計算流程如圖1所示。

圖1 不確定型多屬性群決策的Dice算法

3 算例

某投資銀行決定對該市3家企業進行投資，由4位專家組成群體考查這3家企業，采用社會效益、環境污染和經濟效益等3項指標作為綜合評估依據，以便作出重點投資決策，其中社會效益和經濟效益為效益型屬性指標，而環境污染為成本型屬性指標。假設這3家企業的各項指標值均以區間數形式表示，4位專家群體的決策矩陣分別為

（2）根據式（6）計算4位決策者的理想解權重，分別得到：

因此，可以得到4組權重組成的向量矩陣：

按照式（7）標準化后，得到：

通過Matlab 6.0軟件計算出，式（10）中矩陣STS所對應的最大特征根λmax為0.7212，其對應的特征向量為W**＝（0.3721，0.4929，0.1350）T。

（3）根據式（13），求出4位決策者的系統屬性權重為：

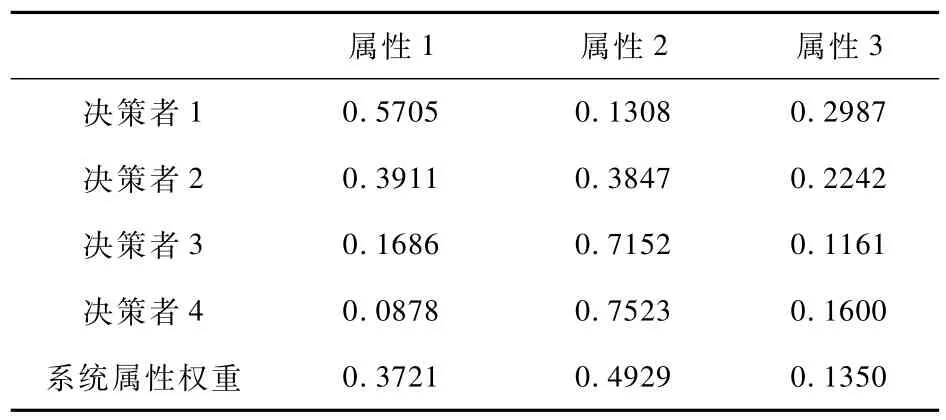
表1 各決策者的屬性權重與系統屬性權重

（4）計算各決策者權重：

根據定義6，求出群體正、負理想解分別為：

計算各決策者權重，如表2所示：

表2 各決策者權重

（5）計算群體綜合決策矩陣為：

（6）根據式（18）計算各方案的Dice相似度分別為：D（X*，X1）＝0.9830，D（X*，X2）＝0.9952，D（X*，X3）＝0.9883。

（7）根據Dice相似度的大小對方案優劣排序為：方案2?方案3?方案1。

4 結束語

本文針對屬性權重和決策者權重均為未知的不確定型多屬性群決策，首先建立各決策者的理想解權重優化模型，然后采用投影模型對各決策者的屬性權重進行非線性集成，進而得到系統屬性權重，同時利用投影模型計算決策者權重，并進一步得到群體綜合決策矩陣，由群體綜合決策矩陣計算出各方案與群體理想解的Dice相似度，然后根據Dice相似度大小確定各方案的優劣排序。目前，針對區間數不確定型多屬性群決策問題，大多數文獻采用TOPSIS法和可能度法，而本文的方法更簡潔與實用。最后，利用實例驗證了整個決策的詳細計算過程。本文的計算過程概念簡單、思路清晰、操作方便，對處理復雜的不確定型多屬性群體決策具有很強的實效性和可操作性。