服務時間變動下的可重入手術調度

王 愷，陳 夏，陳麗君

（1.武漢大學 經濟與管理學院；2.湖北中醫藥大學 信息工程學院）

0 引言

作為醫院內部最為核心的系統，手術系統涉及醫務人員、醫療物資和設備設施等各類手術資源，如何提升其運作效率已成為確保醫院整體收益與服務質量的重要問題。手術調度需要結合手術過程和資源需求，為調度期內亟待進行的手術確定開始時間和分配各類手術資源［1～3］。病人的手術過程通常分為術前準備、手術和術后恢復階段，依次在準備室、手術室和恢復室進行［4，5］。當前國內外的某些醫院受資金、空間的限制或者希望提高床位利用率，不單獨建設準備室和恢復室，而是設置更多的公共床位，可同時用于術前準備和術后恢復。美國明尼蘇達州的梅奧診所就采用了類似的作法［6］，不僅有效減少了特定時段因病人擁塞造成的床位不足，還大幅提高了護理人員的工作效率。

由于病人在術前準備和術后恢復時可進入同一區域使用床位，因此這類特殊的手術系統具有病人可重入的特點。可重入場景常見于生產制造領域，出于工藝的特殊要求，同一工件需要在一些特定的機器上進行多次操作處理，極大地增加了生產調度優化的難度［7］。目前暫未發現有學者進行過可重入手術系統的調度優化研究。

已有的醫院手術調度文獻大都集中在靜態環境下的調度優化問題，而實際手術過程會受醫護人員水平、病人病情和其它各類突發事件干擾，容易出現術前、術中和術后的服務時間偏離預期時間。因此，近年來部分學者開始關注動態環境下的手術調度問題，已有研究主要采用隨機規劃、魯棒優化和模糊規劃的方法進行數學建模。Molina-Pariente等［8］使用多個隨機變量描述急診病人的到達時間和手術時長，建立了用于求解手術室調度問題的混合整數隨機規劃模型。Addis等［9］針對考慮不確定手術時間的手術室計劃與調度問題構建了魯棒優化模型。類似地，周炳海和殷萌［10］以最小最大遺憾作為決策準則，對不確定時間下帶資源約束的手術室魯棒調度問題進行了研究。考慮到醫院手術調度問題的復雜性，學者們通常使用簡單的分派規則和模擬退火算法、禁忌搜索、遺傳算法、蟻群算法等高效的元啟發式方法進行求解［11，12］。目前關于動態環境下的手術調度研究均未同時考慮手術準備時間、手術時間和術后恢復時間的不確定性。

綜上所述，本文將對考慮服務時間變動的可重入手術系統調度進行研究，以最小化病人術后恢復的平均完成時間為目標，構建醫院可重入手術調度的數學優化模型，提出基于經典遺傳算法與變鄰域搜索的自適應混合調度算法，通過塊鄰域和基于輪盤賭的鄰域變換策略增強算法的局部優化性能。當前研究手術調度優化的文獻均未考慮術前準備與術后恢復共同占用床位資源的情況，也未同時考慮術前、術中、術后服務時間變動的情形。

1 問題描述及數學模型

1.1 問題描述

服務時間變動下的可重入手術調度問題可描述為：某醫院擁有M間設備齊全的手術室，公共區域有F張可用于術前準備和術后恢復的床位，可同時為多位病人提供術前、術中和術后的醫療服務。現需要為某工作日亟需手術的N位擇期病人安排手術。病人的手術過程分為三個階段，分別為使用公共區域的床位進行術前準備、手術室手術、術后重新轉移到公共區域的床位上恢復。每個階段的實際服務時長取決于醫護人員水平、手術類型和手術當天病人體征，可能會偏離預期服務時長。本問題的服務時長均采用三角模糊數來描述，即根據醫院的歷史統計數據來確定每位病人每個階段最長、最可能和最短的服務時長。

考慮到生產運作管理與醫療運作管理的相似性，近年來開始有學者將生產運作管理中的理論、模型和方法用于求解手術調度問題［13］。如下圖所示，多間手術室和公共區域的多張床位相當于車間里不同加工階段的多臺并行機，病人為待處理工件，術前、術中和術后的醫療服務可看作柔性流水車間（Flexible Flow Shop，FFS）的三個處理工序。由于病人會先后兩次使用公共區域的床位進行術前準備和術后恢復，因此該調度問題具有可重入特性，可視為可重入FFS調度問題，屬于NP難問題［14，15］。

圖1 病人的手術過程

該問題的數學模型基于以下假設：（1）只對擇期手術進行調度優化，而不考慮急診手術；（2）同一病人選擇不同手術室或不同床位對所需服務時長沒有影響；（3）同一病人術前準備、手術和術后恢復必須連續進行；（4）術前、術中和術后各階段所需資源（人員、藥品、工具等）在開放時段內隨時可用；（5）不考慮病人在手術室和公共區域床位間的轉移時間。

1.2 數學模型

考慮到服務時長的變動，每位病人術前、術中、術后的服務時長與各項服務的開始和結束時間均采用三角模糊數。模型中的符號與變量定義如下：

N：病人數量；

No：手術室數量；

Np：公共區域的床位數量；

pi，1：病人術前準備時長；

pi，2：病人手術時長；

pi，3：病人術后恢復時長；

ti，1：病人術前準備的開始時間；

ti，2：病人的術前準備的結束時間；

ti，3：病人手術開始時間；

ti，4：病人手術結束時間；

ti，5：病人術后恢復的開始時間；

ti，6：病人術后恢復的結束時間；

M：充分大的正數；

基于以上定義，可以得到本文研究問題的數學模型如下：

其中，目標函數（1）為最小化某工作日全部病人術后恢復的平均結束時間；約束（2）、（4）分別保證每位病人只能使用公共區域的一個床位進行術前準備和術后恢復；約束（3）保證每位病人的手術必須在一間手術室內完成；約束（5）、（6）保證公共區域內的任一床位不能同時為多位病人提供術前準備服務；約束（7）確保每間手術室不能同時進行多臺手術；約束（8）、（9）保證公共區域內的任一床位不能同時為多位病人提供術后恢復服務；約束（10）確保同一病人的術前準備、手術和術后恢復連續進行；約束（11）用于確定病人每項服務的結束時間；約束（12）確保病人術前準備時間的合法性；約束（13）規定了決策變量的取值范圍。

由于上述數學模型中采用三角模糊數描述不同服務的服務時長與各項服務的開始和結束時間，目標函數的計算將涉及到三角模糊數的累加、取大、比較等操作。假設b3）均為三角模糊數，累加操作＝（a1+b1，a2+b2，a3+b3）可用于計算每位病人不同階段的服務結束時間，取大操作＝（a1∨b1，a2∨b2，a3∨b3）可得到每位病人不同階段的服務開始時間，比較操作則用于比較同一問題兩個解（手術調度方案）的性能。對于任一三角模糊數本文的比較操作均采用以下三個通用準則［16～18］：

準則1c1（s）＝（s1+2s2+s3）／4，根據c1對和進行比較；

準則2c2＝s2，若的c1相等，則根據c2進行比較；

準則3c3（s）＝s3-s1，若上述兩個準則無法區分，則根據c3進行比較。

2 基于遺傳算法和變鄰域搜索的自適應混合優化算法HGA-AVNS

作為一種模擬生物進化的隨機搜索算法，遺傳算法（Genetic Algorithm，GA）采用選擇、交叉、變異操作達到種群進化［19］。變鄰域搜索（Variable Neighborhood Search，VNS）則基于特定的鄰域變換規則在不同的鄰域中實現高效的局部搜索［19］。由于VNS可以有效避免算法過早收斂，我們提出了基于GA和VNS的自適應混合優化算法（HGAAVNS）。HGA-AVNS通過較為新穎的塊鄰域和基于輪盤賭的鄰域變換策略來增強算法的局部搜索能力。

2.1 編碼、種群初始化、個體選擇

對于當日需要進行手術的n位病人，可基于服務這些病人的先后順序進行編碼。比如，編碼s＝（s（1），s（2），…，s（n））中的s（k）是第k位被服務病人的編號。HGA-AVNS首先隨機生成初始種群，然后通過輪盤賭方法選出較好的個體作為父代。考慮到種群中個體的目標函數值Zi為三角模糊數，我們通過準則1計算其精確值c1（Zi），并將其倒數作為個體適應度值。

2.2 交叉操作

為了更為有效地對解空間進行搜索，HGAAVNS通過兩點交叉法生成子個體。如圖2所示，該方法首先在父個體中隨機選取cut1、cut2兩個交叉點，然后子個體1直接復制父個體2中cut1、cut2間的病人，最后其它位置依次復制父個體1中未被復制的病人；子個體2也采用類似的方法生成。

圖2 兩點交叉示例

2.3 變異操作

為了保持種群中個體的多樣性，HGA-AVNS通過插入變異生成新個體。如圖3所示，對選中的個體隨機選取delete和insert兩個位置，將delete位的病人插入到insert位的病人之前。

圖3 插入變異示例

2.4 自適應變鄰域搜索

為了有效提高HGA-AVNS的局部搜索能力，本文提出了一種全新的自適應變鄰域搜索（Adaptive Variable Neighborhood Search，AVNS）算法。該算法采用了6種基于塊的鄰域結構進行局部搜索，并通過自適應的鄰域變換規則動態地選擇表現較好的鄰域結構。

2.4.1 基于塊的鄰域結構

病人術前準備和術后恢復都會使用公共區域的床位，如果因為床位不足而導致部分病人無法及時進行術前準備，則會出現即使有空閑的手術室也無法實施手術的情況。考慮到上述場景，我們把需要進行手術的病人分為等待與無等待兩類。等待病人指因公共區域空閑床位不足使得所分配手術室處于等待狀態的病人，無等待病人指在所分配的手術室可以連續進行手術的病人。通過將病人進行分類，可以將種群中的每個個體分解成多個病人塊，其定義如下：

塊：個體（病人序列）由包含n位需要進行手術的病人組成，等待病人將個體分成m個集合，即病人塊。塊內的第一位病人為塊首，最后一位病人為塊尾。在每一個塊內，除了塊首，其余病人全部是無等待病人。

本文研究的醫院手術調度可看作生產制造領域的可重入FFS調度。對于FFS調度問題，已有研究中常用的鄰域結構（Neighborhood Structure，NS）主要包括插入鄰域、互換鄰域與逆序鄰域等。根據塊的定義和調度問題常用的鄰域，本文采用下面6種基于塊的NS來實現局部搜索：

（1）NS1：在隨機選中的一個塊內使用插入操作，即在塊內隨機選取一位病人并將其隨機插入到塊內的其它位置；

（2）NS2：在隨機選中的一個塊內使用互換操作，即在塊內隨機選取兩位病人并互換位置；

（3）NS3：在隨機選中的一個塊內使用逆序操作，即在塊內將隨機選取的兩位病人之間的所有病人進行逆序排列；

（4）NS4：若個體中塊的數量m＞1，首先從前m-1個塊中隨機選取一個，然后將它的塊尾和后面相鄰塊的塊首互換；否則，保持個體不變；

（5）NS5：若個體中塊的數量m＞1，首先從前m-1個塊中隨機選取一個，然后將它和后面相鄰塊的塊首互換；否則，保持個體不變；

（6）NS6：若個體中塊的數量m＞1，首先從前m-1個塊中隨機選取一個，然后將它和后面的相鄰塊互換；否則，保持個體不變。

上述6種NS主要對塊內或塊間的病人進行調整，以期通過減少塊的個數來降低等待病人的數量與提高手術室的利用率。

2.4.2 隨機擾動和局部搜索

對于一個特定的當前解x，隨機擾動過程會根據所選取的NS生成一個新的鄰域解x′，從而避免HGA-AVNS的種群過早收斂。NS的選擇過程可詳見2.4.3鄰域變換。

在對當前解x進行隨機擾動后，對新的鄰域解x′進行局部搜索。與隨機擾動類似，該過程仍然是在當前選中的NS中進行，以期獲得手術調度問題的局部最優解。HGA-AVNS采用常見的 firstimprovement局部搜索方法。該方法不斷生成x′在當前鄰域結構中的鄰域解xn，若xn優于x，則x＝xn并更新當前局部最優解，重復上述過程直至連續迭代5次后局部最優解沒有改變。

2.4.3 鄰域變換

HGA-AVNS的局部搜索性能不僅取決于所使用的NS，還會受不同NS間搜索順序的影響。經典VNS一般先將NS按照其規模與復雜度進行排序，然后根據事先定義的規則更換鄰域進行局部搜索，這些規則通常不根據所生成鄰域解的優劣來確定NS，往往導致局部搜索效率不高。而HGA-AVNS則使用了全新的自適應鄰域變換規則，可以根據6個塊鄰域生成鄰域解的優劣來動態選擇合適的NS。

在該規則中，每次鄰域變換均要考慮當前鄰域的搜索效果。鄰域集合｛NS1，NS2，…，NS6｝中的任一鄰域NSk都有一個選中概率pk，其計算公式如下：

其中，ck和sk分別為使用Nk進行局部搜索的次數和得到更好的解的次數，m為一個非常小的正數以避免pk為零，Rk為多次通過Nk進行局部搜索時找到更好的解的比例。每個塊鄰域的選中概率均初始化為1／6，當所有鄰域遍歷一次后，pk可按式（14）～（15）進行更新，能夠找到更多更好鄰域解Nk的被選中的概率就越大。在各鄰域的pk更新之后，我們使用輪盤賭的方法來更換鄰域。

2.5 HGA-AVNS算法求解過程

步驟1初始化HGA-AVNS算法參數，主要包括HGA-AVNS的最大進化代數G1，種群規模PS，交叉率Pc，變異率Pm，AVNS的最大迭代次數G2；

步驟2隨機生成由PS個個體組成的初始種群，將其中最好的個體作為當前全局最優解πb，設定HGA-AVNS中的當前迭代次數g1＝1；

步驟3執行基于輪盤賭的選擇操作；

步驟4根據交叉率Pc執行兩點交叉操作：

步驟5根據變異率Pm執行插入變異操作：

步驟6選出當前種群中的最優個體π，執行AVNS進行局部搜索。設定AVNS中的當前迭代次數g2＝1，令π為AVNS最優解πm的初始值。如果g2≤G2，重復步驟6.1～6.3；否則，輸出；

步驟6.1鄰域變換：根據式（14）更新6種NS的選擇概率pk，并采用輪盤賭方法確定一種鄰域結構NSk，并更新其被選中次數ck＝ck+1；

步驟6.2隨機擾動：根據所選的NSk，生成π的一個鄰域解π′；

步驟6.3局部搜索：根據所選的NSk，對π′進行該鄰域內的局部搜索，得到局部最優解π″，則g2＝g2+1；若π″優于π，則π＝π″，sk＝sk+1；若π″優于

步驟7將AVNS得到的替代種群變異后的最差個體。若優于πb，則πb＝。同時使用精英保留規則，用πb替代種群中的最差個體；

步驟8令g1＝g1+1。若g1≤G1，將更新后的種群作為下一次迭代的輸入，轉至步驟3；否則，輸出最優解πb。

3 實驗結果與分析

為驗證HGA-AVNS求解服務時間變動下可重入手術調度問題的有效性，本文先通過田口實驗確定HGA-AVNS主要參數的取值，再對比HGAAVNS與其它幾種算法的優化性能。所有的優化算法全部采用MATLAB 2016a實現，實驗測試環境配置為InteCoreTMi7 4GHz CPU和4GB RAM。

3.1 實驗數據

考慮到服務時間變動下的可重入手術調度暫無國際公認的測試算例，本文基于多家醫院的歷史數據與已有的手術調度研究［20］，采用以下數據生成測試算例，其中服從均值為180分鐘、標準差為60分鐘的對數正態分布［16］*rand（）；pi，3＝，其中服從均值為-10分鐘、標準差為15分鐘的對數正態分布［16］，rand（）為0-1間均勻分布的隨機數。通過遍歷No，Np，N的所有組合共產生4×2×2＝16個測試問題。

3.2 關鍵參數實驗分析

HGA-AVNS為混合元啟發式方法，其優化性能受到G1、PS、Pc、pm和G2等算法參數影響。本文選取一個中等規模的手術調度問題（No＝13，Np＝15，N＝30），首先使用田口實驗方法對算法參數的靈敏性進行分析，然后確定HGA-AVNS上述四個參數的取值。

HGA-AVNS關鍵參數的因子水平為G1＝｛50，100，150，200｝、PS＝｛50，100，150，200｝、Pc＝｛0.6，0.7，0.8，0.9｝、Pm＝｛0.03，0.05，0.07，0.09｝、G2＝｛50，70，90，110｝。如表1所示，采用L16（45）正交表，共計16組典型參數組合。對于選定的中等規模問題，采用特定參數組合的HGA-AVNS分別求解10次，計算目標函數的平均值Z*，并通過準則1得到其精確值c1（Z*）。基于表1中的c1（Z*），圖4描述了各參數不同取值對HGA-AVNS優化性能的影響。由圖4可知，HGA-AVNS參數的最佳取值為G1＝200，PS＝200，Pc＝0.7，Pm＝0.03，G2＝70。

表1 田口實驗設計和實驗結果

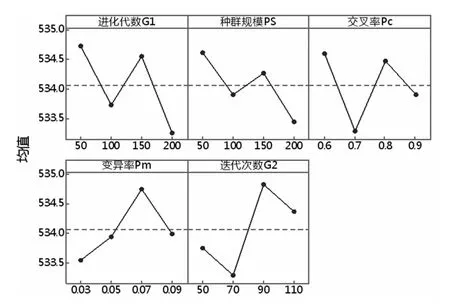
圖4 實驗設計均值主效應圖

3.3 算法性能實驗分析

針對服務時間變動下的可重入手術室調度問題，本文將HGA-AVNS與其它三種調度算法進行了對比：（1）最短服務時長規則（Shortest Service Time，SST）：優先為手術時長短的病人提供術前、術中和術后服務；（2）經典GA：選擇、交叉、變異操作和HGA-AVNS相同；（3）GA-VNS：與HGA-AVNS的唯一差別在于使用傳統的鄰域變換規則，即從第一個鄰域NS1開始，若在某鄰域NSk內進行搜索后獲得的新解優于當前解，則重新回到中搜索；否則，在下一個鄰域NSk+1中繼續搜索。

為了更加公平地對比優化算法性能，GA和GAVNS的主要參數取值與HGA-AVNS相同。對于每個測試問題，SST只求解1次，而GA、GA-VNS和HGAAVNS分別求解10次。表2給出了16個測試問題不同優化算法的測試結果。其中，Z*為解的均值，c1（Z*）為使用準則1得到的精確值，Dev為算法性能的相對偏差。Dev的計算公式為其中和分別為SST、GA、GA-VNS和HGA-AVNS得到的解或解的均值。

通過分析表2中各優化算法的Z*、c1（Z*）和Dev，我們可以得出下面的結論：（1）按優化性能從優到劣依次為HGA-AVNS、HGA-VNS、GA、SST；（2）三種元啟發式算法得到的解明顯好于SST；（3）在GA、HGA-VNS和HGA-AVNS三種元啟發式算法中，GA性能最差，表明對于本文所求解的手術室調度問題混合啟發式算法優于單一啟發式算法；（4）對于多數測試算例，HGA-AVNS求得的解要好于HGA-VNS，說明在GA和VNS的混合優化算法中引入高效的鄰域變換規則能夠增強算法的優化性能。

表3給出了上述幾種算法的CPU運行時間（單位為秒）。對于16個測試問題，算法的平均運行時間按由短到長排序分別為SST、GA、HGAVNS、HGA-AVNS。SST是一種十分簡單的分派規則，運行時間較短，但優化性能較差。GA、HGAVNS和HGA-AVNS均為元啟發式算法，通過種群的不斷進化實現隨機搜索，優化性能較好，但是運行時間偏長。特別地，作為混合優化算法，由于HGA-VNS和HGA-AVNS在GA里嵌入了VNS來提升局部搜索性能，導致它們的運行時間比GA稍長。與HGA-VNS相比，HGA-AVNS運行時間稍短。綜合表2和表3的實驗數據，盡管HGA-AVNS的求解時間稍長，但是優化性能最佳。

表2 不同規模問題下SST、GA、HGA-VNS、HGA-AVNS的測試結果

表3 不同規模問題下SST、GA、HGA-VNS、HGA-AVNS的運行時間

4 結論

對于服務時間變動下的可重入手術調度問題，本文使用三角模糊數描述術前、術中和術后的服務時長，以最小化病人術后恢復的平均完成時間為目標，構建了術前和術后共用床位的可重入手術調度模型，設計了基于GA和VNS的自適應混合優化算法HGA-AVNS。為了提高HGA-AVNS的局部搜索性能，設計了六種塊鄰域，并采用基于輪盤賭的方法動態選擇合適的鄰域進行搜索。最后通過一組測試算例比較了多個優化算法的性能，驗證了所提算法的優越性。

本文將可重入生產系統的特性引入至醫院的手術調度問題中，不但擴大了可重入理論的應用領域，而且提高了手術系統的穩定性和醫療設施的利用率。我們尚未考慮緊急手術、醫療資源有限等情況，因此未來可以在醫院動態手術條件下同時考慮不同類型的醫療資源約束，進一步加強本文所提出的模型和算法的實用性。