一種面向熱設計的反饋-模糊推理全局算法

雷飛 張天昊

摘 ? 要：針對常規模糊推理算法無法有效求解具有復雜或未知傳熱規律的傳熱學反問題，提出一種反饋-模糊推理全局算法. 基于模糊推理的基本流程，將變論域方法、反饋思想和模擬退火算法結合起來，通過反饋單元降低模糊規則對傳熱規律的依賴，并通過模擬退火單元防止陷入局部最優. 采用此方法對風冷散熱器翅片的幾何結構設計問題進行求解，并與常規模糊推理算法和模擬退火算法結果進行對比. 同時，對不同初始值、不同輸入誤差下反饋-模糊推理全局算法的計算結果進行驗證和對比. 結果表明，該算法可以解決傳熱學規律復雜或未知的傳熱學反問題，計算結果不受初始值影響. 該算法在解決此類問題時擁有良好的魯棒性和抗不適定性，可以為反問題、結構設計和優化提供參考.

關鍵詞：傳熱;反問題;模糊推理;純電動汽車;全局優化

中圖分類號：TK124 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

A Feedback-fuzzy Inference Global Algorithm for Thermal Design

LEI Fei?，ZHANG Tianhao

（State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University，Changsha 410082，China）

Abstract：Conventional fuzzy inference algorithms cannot effectively solve the inverse heat transfer problems with complex or unknown heat transfer laws. In this paper， a feedback-fuzzy inference global method is proposed. Based on the basic process of fuzzy inference， variable universe method， feedback thought and simulated annealing algorithm are combined. The dependence of fuzzy rules on heat transfer law is reduced by feedback unit， and the local optimum is prevented by simulated annealing unit. This method was employed to solve the geometric structural design problem of air-cooled radiator fins. The results were compared with those of conventional fuzzy inference and simulated annealing algorithm. And the results of feedback-fuzzy inference global method under different initial values and input errors were verified and compared. The results showed that the proposed method could solve the inverse heat transfer problem with complicated or unknown heat transfer law， and the results were not affected by initial values. The method demonstrates robustness and resistance to ill-posed problems， which can provide a reference for inverse problems， structural design and optimization.

Key words：heat transfer;inverse problem;fuzzy inference;battery electric vehicle;global optimization

電動汽車電機控制器內部的集成化程度越來越高，控制器內元器件的發熱量不斷增加. 在有限的物理空間內，多合一控制器中大功率元件的熱通量可達200 ～ 300 W/cm2. 過高的溫度會直接損壞元器件，熱設計和熱管理成為集成控制器設計的關鍵環節[1].

熱設計問題通常是已知目標溫度來求解相關設計參數，本質上屬于已知目標溫度求解幾何邊界的傳熱學反問題[2]. 通常基于傳熱系統的局部測量溫度信息，求解系統的熱流密度、熱源參數、熱物理參數和幾何參數等難以測量的未知參數的問題. 在控制器熱設計問題中，由于大量電子電器元件高度集成導致其傳熱規律復雜，難以得到傳熱學規律的定性描述. 復雜的傳熱規律是該問題的典型特點之一.

不適定性是傳熱學反問題的另一特點. 這種不適定性是指該問題在Hadamard意義下解的唯一性、存在性和穩定性不能同時得到滿足[3]. 一方面，由于輸入信息不全面，反問題的解可能不存在或不唯一;另一方面，由于輸入信息存在偏差，輸入信息的誤差在反問題的求解過程中會被放大，從而導致反問題的解往往存在不穩定性. 反問題的不適定性為求解帶來了較大挑戰.

傳熱學反問題的求解方法可分為非迭代法和迭代法. 非迭代法依據已知的測點信息和待求解量之間的數學關系，直接通過已知量計算待反演參數，無需反復計算正問題以修正計算結果，可實現較高的計算速度. 吳國鵬等[4]基于最小二乘法和誤差函數反演了功能梯度材料熱源發熱功率;Yu等[5]將最小二乘法和邊界元法相結合提高算法的抗不適定性并對鍋爐內壁的幾何邊界進行了反演;Yu等[6]利用邊界元法分別在穩態下和瞬態下對爐內壁的邊界條件進行識別. 對于復雜傳熱學問題，由于已知條件和待求解量之間的數學關系建立存在困難，該類方法應用有限，同時存在不適定性問題.

迭代法可分為梯度法和非梯度法，其中經典的梯度法有最速下降法（Steepest Descent Method，SDM）、共軛梯度法（Conjugate Gradient Method，CGM）、Levenberg-Marquardt 法（L-M）等. Huang等[7]通過SDM成功反演了翅片換熱器的換熱系數;Yang等[8]采用改進的L-M法估算了傳熱學反問題中的導熱系數;Xiong等[9]應用CGM反求了二維傳熱系統中的熱流量;王堃等[10]用正則化CGM估計了二維穩態傳熱邊界溫度分布.

梯度法可以解決部分傳熱學反問題，但當傳熱規律較為復雜時會陷入局部最優，且問題的可微性不能保證. 此外，如果測量信息不完整或存在測量誤差，梯度法的求解結果可能出現惡化[11].

非梯度法具有良好的抗不適定性能力和全局搜索能力，但計算量較大. 這類方法有遺傳算法、蟻群算法等，近年來隨著計算技術的發展而得到較廣泛應用. Lee等人[12]利用粒子群優化方法估計介質的輻射特性;Liu[13]用一種改進的遺傳算法估算瞬態傳熱系統的平板熱源功率;Parwani[14]等人利用差分進化算法估算了傳熱系統中熱源的發熱功率和位置.

模糊推理是20世紀60年代Zadeh提出的一種啟發式算法[15]. 它是在模糊集合論基礎上對人腦的決策和判斷做定量研究的一種不確定推理方法. 該算法只需從單一起始點開始計算，相對于蟻群算法、遺傳算法等需要多個初始點的非梯度類算法而言計算成本較低，具有良好的抗不適定性，能有效抵抗輸入信息的干擾[16]. 此外，模糊推理算法可以有效利用不精確和不完整的信息[17]. 這些特點在解決包括傳熱學反問題在內的不適定問題時具備優勢. Wang等[18]提出了分散模糊推理算法用來求解熱傳導反問題中的幾何參數;Krzywanski等[19]利用模糊推理算法預測了大型循環流床的導熱系數;Chen等[20]提出一種具有目標跟蹤能力和降噪性能的智能加權模糊推理算法，并將其應用于空心復合管的熱傳導幾何參數反演問題中;姜曙等[21]利用分散模糊推理對圓筒熱傳導問題的幾何邊界進行了反演. 在以上傳熱規律明確的問題中，模糊推理方法均取得了較好的結果.

但是，常規模糊推理方法中模糊規則的制定對傳熱學規律的認知依賴程度較高，在求解傳熱學規律未知或其定性描述為非單調的傳熱學反問題時，常規模糊推理算法會由于無法制定模糊規則而失效.

本文針對傳熱學規律未知或非單調的傳熱學反問題提出一種改進的模糊推理算法，該算法以變論域模糊推理方法為基礎，結合反饋算法和模擬退火算法的優勢，不僅降低對初始論域依賴性，同時降低模糊規則對傳熱規律認知的依賴性. 使用該方法對電動汽車集成控制器的風冷散熱器進行設計，并討論初始值和測量誤差對該方法的影響.

1 ? 算法描述

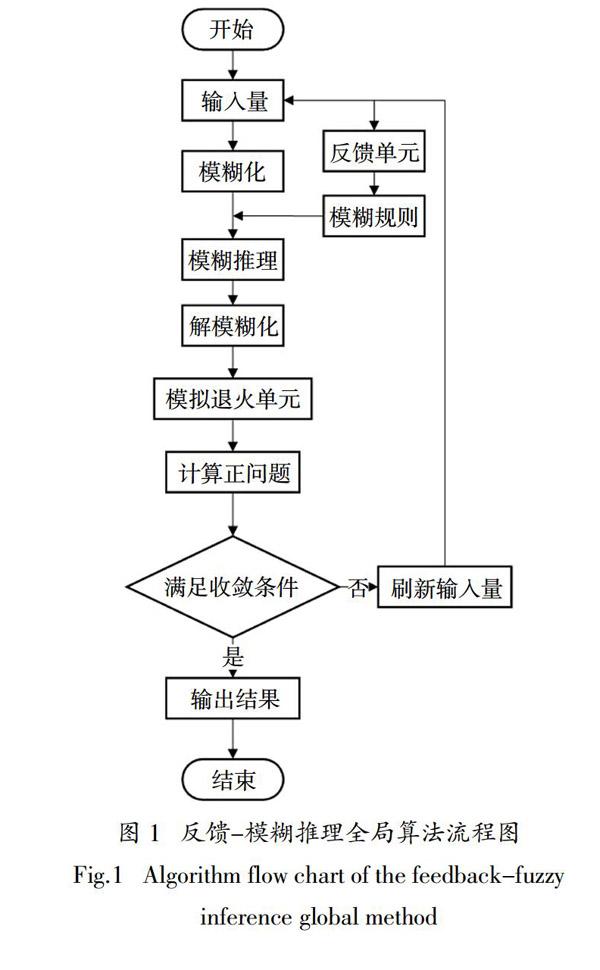
反饋-模糊推理全局算法由模糊推理單元，反饋單元和模擬退火單元組成.

該算法的輸入輸出為：輸入量e = Tmea0 - Tcal，其中Tmea0為測點溫度，Tcal為每次迭代過程的計算溫度. 對應輸入、輸出論域的語言值有零（ZO）、正小（PS）、正中（PM）、正大（PB）. 輸出量的大小由其對應的論域和模糊規則決定，符號由反饋單元根據前一步迭代的計算結果決定. 這種輸出決定方式可以降低模糊推理輸出值對傳熱學規律的依賴.

若傳熱學反問題的傳熱規律較復雜或未知，則可以通過模擬退火單元防止結果陷入局部最優. 記uk（i）為模糊推理單元第i次迭代的輸出，n（i）為待求解量第i次迭代的計算結果，Tcal（i）為第i次迭代的計算溫度，迭代結束條件為Tmea0 - Tcal≤ε，ε為收斂條件. 算法的流程如圖1所示.

2 ? 問題描述

圖2為某電動汽車集成控制器的簡化幾何模型，該控制器箱體外形尺寸為388 mm×288 ?mm×124 mm，芯片為方形均勻體熱源，為模擬芯片封裝，在元件外部增加聚苯硫醚（Polyphenylene sulfide，PPS）材料外罩;用各向異性材料模擬印制電路板（Printed Circuit Board，PCB）;IGBT為導熱性良好的均勻方形體熱源;為模擬IGBT的水冷，將箱體底部設為333 K恒溫邊界，其余的面設為298 K恒溫邊界;箱體材料及翅片散熱器材料選用鋁材，各材料物性參數見表1;系統內熱源及其發熱功率見表2;風冷散熱器尺寸結構如圖3所示.

未安裝風冷散熱器時1、2、3號芯片溫度分別為392、411、389 K，其中2號芯片的溫度超過了設計要求的393 K，故對安裝在PCB下方風冷散熱器的翅片數量進行設計，使2號芯片溫度降至378 K. 該問題本質上屬于已知測點溫度求解幾何邊界的傳熱學幾何反問題，即求解翅片數量n使得Tmea - Tcal≤ε，其中Tmea為2號芯片的目標溫度，Tcal為每次迭代過程的計算溫度，ε為迭代停止閾值或收斂條件，由于該問題中的目標溫度精度要求為1 K，故在此ε取值為1.

該傳熱系統中同時存在熱傳導、熱對流、熱輻射，假定在控制器內的空氣為理想氣體，其流動為三維湍流流動，且忽略輻射換熱，則正問題的控制方程如下.

熱傳導方程：

[Δ]2T = 0 ? ? ?（1）

熱對流質量守恒方程：

[Δ]V = 0 ? ? ?（2）

熱對流動量守恒方程：

ρ = F - [Δ]P + η[Δ]2V ? ? ? ? ? （3）

熱對流能量守恒方程：

ρcp = λ[Δ]2T ? ? ? ? ? （4）

式中：V為流體速度;T為流體溫度;F為體積力;P為壓力;τ為時間;ρ、λ、η和cp分別為流體的密度、熱導率、動力黏度和比熱容.

由式（1）～式（4）可知，由于該問題為熱傳導和熱對流共存的復合傳熱問題，傳熱規律較為復雜.

3 ? 反饋-模糊推理全局算法

3.1 ? 模糊推理單元

模糊推理是以模糊集合理論為基礎，結合計算機語言規則和先驗知識，模仿人類思維進行判決的不確定推理方法，其本質是將一個給定輸入空間通過模糊邏輯映射到一個特定的輸出空間的計算過程.

模糊推理算法的具體模塊有模糊化、模糊規則的制定、模糊推理和解模糊化，如圖4所示.

3.1.1 ? 模糊化

模糊推理的輸入變量e = Tmea - Tcal，其取值范圍是[0，15]，單位為K. 翅片數量為n，其取值范圍為[5，25]，模糊推理的輸出變量uk 是n的補償量，取值范圍為[0，q]. q的取值方式如下：

q = 5e0.3，e > 2

1，e ≤ 2 ? ? ? ?（5）

上述可變輸出域可以保證輸出域的大小與輸入量e正相關，從而在e較大時提高迭代速度，在e較小時提高推理精度并且保證推理的穩定性，減少初始域對輸出的影響.

輸入變量e和輸出變量uk的論域分別劃分為4個模糊等級，對應的語言值為零（ZO）、正小（PS）、正中（PM）、正大（PB）. 采用三角形隸屬度函數，此時輸入論域、輸出論域及其對應的隸屬度函數分別如圖5和圖6所示.

3.1.2 ? 模糊規則的制定

一般來說，帶翅片的風冷散熱器的傳熱規律可定性描述為：當底板面積一定，翅片數量在一定數量范圍內時，散熱效果隨翅片數量增加而增強;超過某一數量范圍，增加散熱翅片時，散熱效果會因風阻而降低. 理論上，這是一個單極值問題，但由于本傳熱系統中的眾多其他熱源會對翅片散熱效果產生影響，因此傳熱規律不能簡單地做定性描述. 這種情況下常規模糊推理會因模糊規則不明確而失效. 本文提出的反饋-模糊推理全局算法中模糊規則僅用來確定輸出值的大小，此時模糊規則的制定僅影響計算效率. 不考慮傳熱規律的模糊規則如下：

1）If e is PB then uk is PB，

2）If e is PM then uk is PM，

3）If e is PS then uk is PS，

4）If e is ZO then uk is ZO

3.1.3 ? 模糊推理和解模糊化

本文采用Mamdani法作為模糊推理方法，定義μA（e）、 μB（μk）分別為輸入變量和輸出變量對應模糊集的隸屬度函數，μC（uk）為模糊推理結果，計算過程可表示為：

μC（uk） = max{min[ μA（e）μB（uk）]} ? ? ?（6）

解模糊化方法采用重心法，計算公式為：

uk =μC（uk）ukdu /μC（uk）du ? ? ?（7）

3.2 ? 反饋單元

根據反饋的基本思想，每次迭代的計算結果都將傳遞給該單元進行判斷，若優于當前結果，則采納該結果;若劣于當前結果，則重新選取補償方向. 利用反饋單元對補償量符號進行判斷的代碼如下，其中r為隨機數.

Start

if i > 1，

if Tcal（i） - Tcal（i - 1） < 0，

uk（i）/uk（i）= uk（i - 1）/uk（i - 1）;

else if Tcal（i） - Tcal（i - 1） > 0，

uk（i）/uk（i）= -uk（i - 1）/uk（i - 1）;

else if Tcal（i） - Tcal（i - 1） = 0，

uk（i） = 2（r - 0.5）;

n（i） = n（i - 1） + uk（i）;

if n（i） < -4，

n（i + 1） = -4 + 0.5r;

if n（i + 1） > 16，

n（i + 1） = 16 - r;

End

End

3.3 ? 模擬退火單元

模擬退火算法是一種基于蒙特卡羅迭代求解策略的隨機優化方法. 該算法模擬了固體退火規律，結合溫度下降過程中的概率跳躍，隨機搜索目標函數的全局最優解. 當問題的傳熱學規律定性描述為單極值問題時可不使用此單元. 由于本研究中反問題的傳熱學規律未知，為避免陷入局部最優，故在反饋單元的基礎上加入模擬退火單元進行全局求解.

設置當前退火溫度為T，退火初始溫度 T2 = 90 ℃，退火結束溫度T3 = 89.9 ℃，降溫方式采用等比例降溫，比例系數j為0.999，結果接受準則為：

當Tcal（i） - Tcal（i-1） < 0時，接受當前結果;當Tcal（i） - Tcal（i-1） ≥ 0時，如果rand < e，接受結果，否則不接受.

3.4 ? 計算過程

Step1 ? 設置模糊推理的輸入量e與輸入論域，輸出量uk與輸出論域，初始化迭代次數i = 1;

Step2 ? 進入模糊推理模塊求解uk（i），令n（i+1）= n（i）+ uk（i）;

Step3 ? 根據n（i+1）計算正問題，得到Tcal（i+1）和e（i+1）;

Step4 ? 判斷e（i + 1）≤1或T < T3是否滿足，如果滿足，終止迭代并輸出n（i + 1），否則i = i + 1，迭代繼續;

Step5 ? 重復Step2—Step4，當i ≥ 2時進入反饋單元和模擬退火單元;

Step6 ? T2 = T2 × j;

Step7 ? 重復Step4;

Step8 ? 重復Step2—Step7.

4 ? 計算結果及討論

4.1 ? 計算結果及驗證

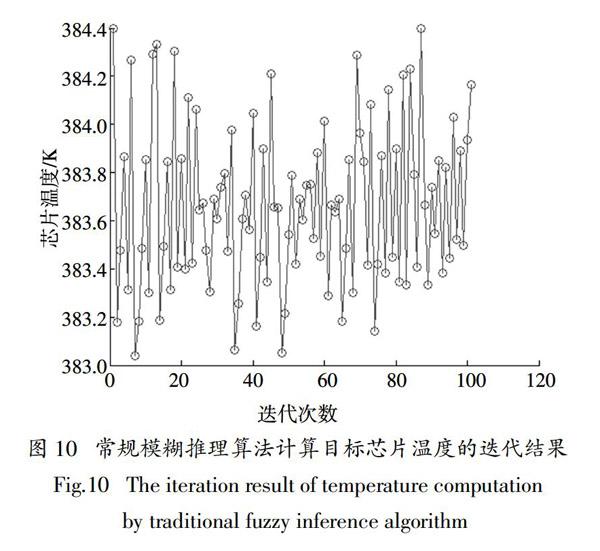
當初始翅片數為25時，使用反饋-模糊推理全局算法和模擬退火算法計算翅片數和目標芯片溫度的迭代結果分別如圖7和圖8所示. 在相同的輸入、輸出論域條件下，使用常規模糊推理計算翅片數和目標芯片溫度的迭代結果分別如圖9和圖10所示.

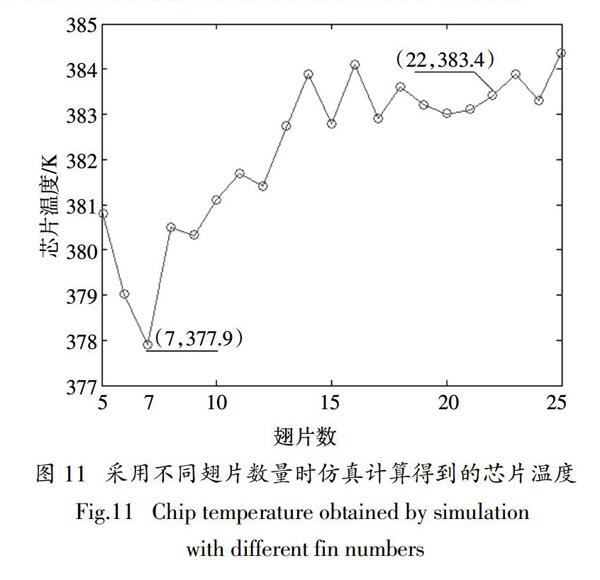
為了驗證算法的準確性，本文通過仿真計算了采用不同翅片數時芯片溫度的情況，如圖11所示.

由圖7和圖8可見，使用模擬退火算法得到翅片數量n=6.5，2號芯片溫度為378.6 K，取整數得n=7;使用反饋-模糊推理全局算法得到翅片數量n=6.9，2號芯片溫度為377.9 K，取整數得n=7. 反饋-模糊推理全局算法在第9次迭代時迭代終止，模擬退火算法在第19次迭代時終止，故反饋-模糊推理全局算法的計算效率高于模擬退火算法.

由圖9和圖10可見，使用常規模糊推理算法得到翅片數量n=22.34，2號芯片溫度為383.57 K，取整數得n=22. 由圖11可知n=22時2號芯片溫度為383.4 K，n=7時2號芯片溫度為377.9 K. 常規模糊推理算法在相同條件下無法得到正確結果.

由圖11可知，反饋-模糊推理全局算法結果準確且有效避免了局部最優，反演精度略高于模擬退火算法.

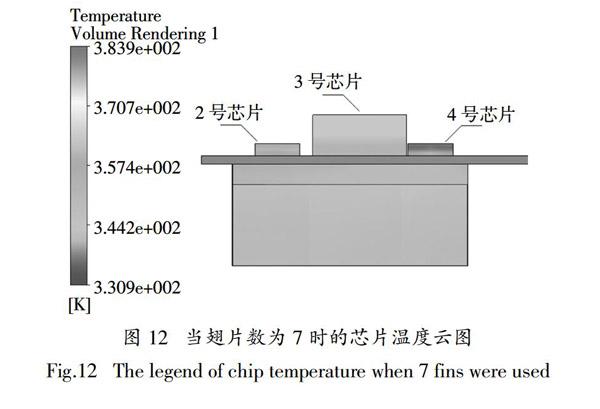
綜上所述，反饋-模糊推理全局算法可以有效求解傳熱學規律無法定量描述的傳熱學反問題，避免陷入局部最優，其計算精度和迭代效率均高于設置相同的模擬退火算法. 利用反求結果得到的最佳翅片數量n=7進行仿真，得到的芯片溫度云圖見圖12，3個芯片最高溫度均低于393 K，結果符合要求.

4.2 ? 初始值對結果的影響

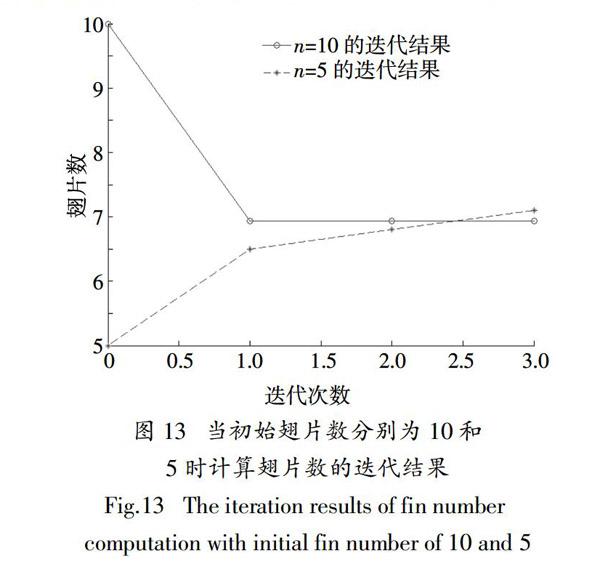
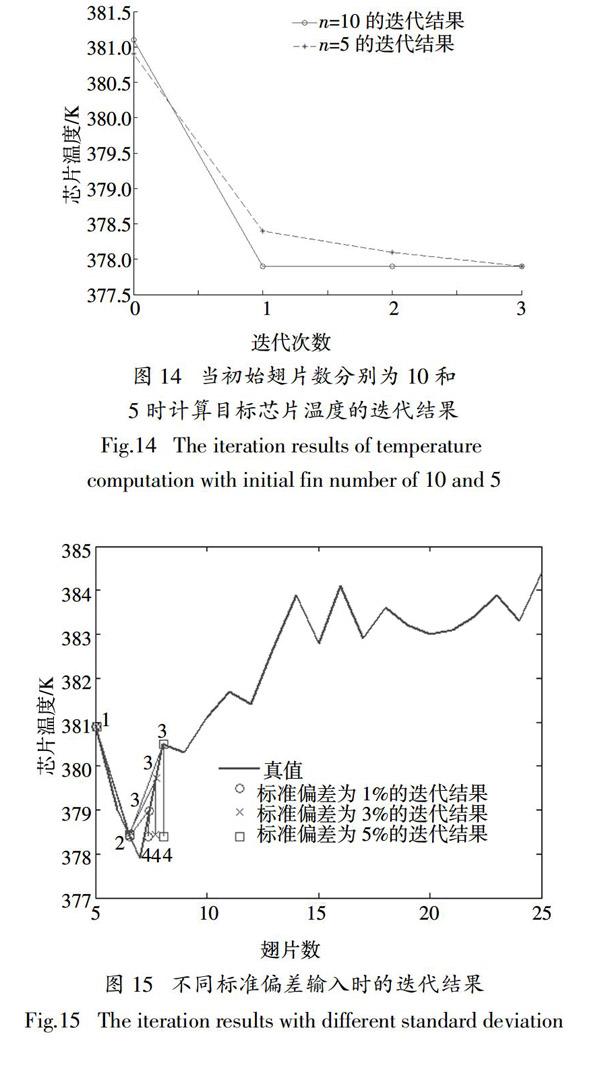
使用反饋-模糊推理全局算法在初始翅片數n（0）分別為10和5時，計算翅片數的迭代結果和目標芯片溫度的迭代結果分別如圖13和圖14所示.

由圖13可知，初始翅片數n（0）分別為10和5時的迭代結果均為n = 7，可見對于相同的設計問題，初始值只影響迭代次數，不影響迭代結果.

4.3 ? 溫度測量誤差對結果的影響

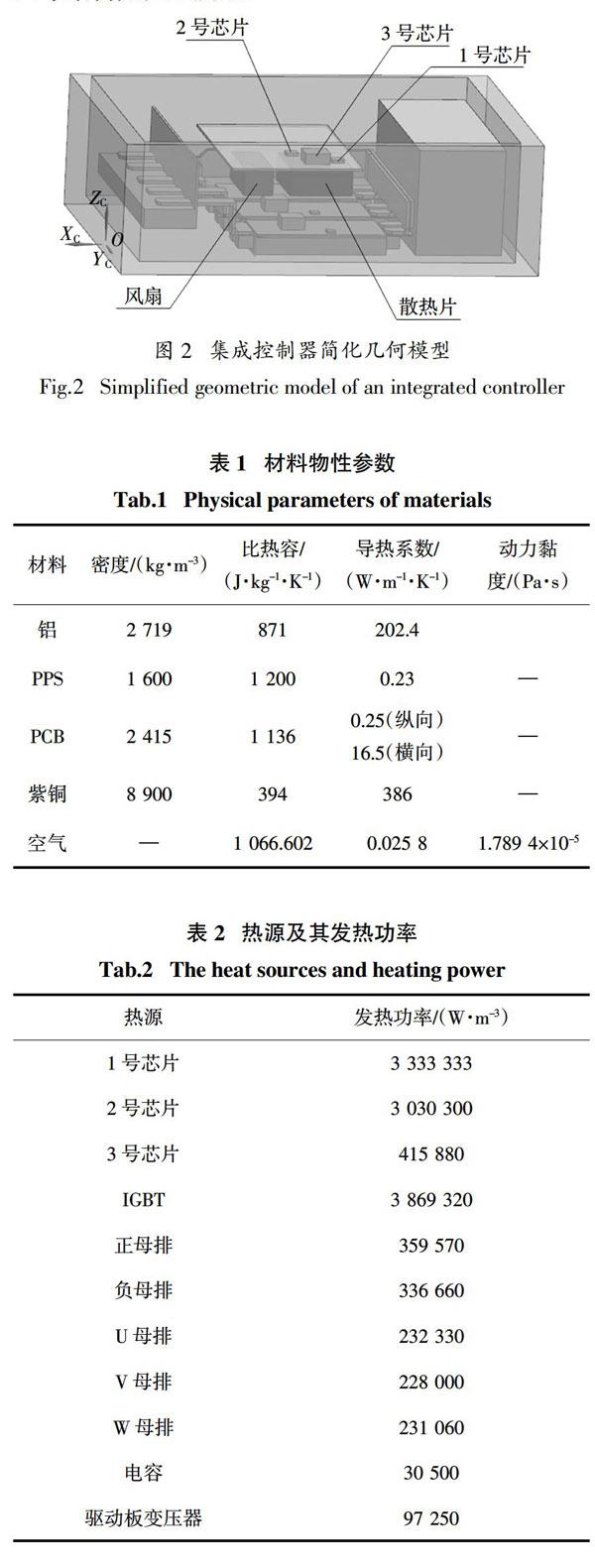
給2號芯片的溫度添加隨機測量誤差Tmea =Tmea + ξ × r，其中ξ是測量誤差的標準偏差，r是一個取值范圍在[-1，1]的隨機數，當ξ分別為1%、3%、5%時，迭代結果如圖15所示. 由圖15可知，在計算過程中隨迭代次數的增加，誤差對迭代結果的影響逐漸增大. 當ξ分別為1%、3%、5%時的最終迭代結果分別為n = 7.22、7.75、7.94，反演偏差在可接受范圍之內，該算法可以有效對抗輸入信息誤差.

5 ? 結 ? 論

本文針對常規模糊推理方法的局限性提出了一種結合模糊推理、反饋思想和模擬退火算法的反饋-模糊推理全局算法，并從傳熱學反問題的角度對電動汽車集成控制器中風冷散熱器的幾何結構設計問題進行了求解.

計算結果表明，相對常規模糊推理算法，反饋-模糊推理全局算法可以應用于非單調或無法定性描述傳熱學規律的熱設計問題中，且具有迭代精度高、收斂速度快、計算結果受初始值影響小等特點. 通過討論輸入誤差對計算結果的影響驗證了該算法具有良好的魯棒性和抗不適定性.

該反饋-模糊推理全局算法拓展了模糊推理方法的應用范圍，可以為反問題、結構設計和優化提供參考.

參考文獻

[1] ? ?楊東升，丁曉紅，季學榮，等. 基于自適應成長法的散熱通道構建技術[J]. 中國機械工程，2012，23（12）：1404—1407.

YANG D S，DING X H，JI X R，et al. Construction technology of cooling channel based on adaptive growth method[J]. China Mechanical Engineering，2012，23（12）：1404—1407. （In Chinese）

[2] ? ?劉慧開，楊立，孫豐瑞. 基于傳熱反問題的異步電機參數估計方法研究[J]. 中國電機工程學報，2006，26（22）：151—156.

LIU H K，YANG L，SUN F R. Estimate method for parameters of asynchronous motor based on inverse heat conduction problem analysis[J]. Proceedings of the CSEE，2006，26（22）：151—156. （In Chinese）

[3] ? ?ALIFANOV O M. Inverse heat transfer problems[M]. Berlin：Spring-Verlag，1994：33—35.

[4] ? ?吳國鵬，徐闖，李英健，等. 一種新的熱源強度識別的非迭代方法研究[J].工程熱物理學報，2020，41（9）：2233—2240.

WU G P，XU C，LI Y J，et al. Research on a novel non-iterative inverse method for identifying the strength of heat source[J]. Journal of Engineering Thermophysics，2020，41（9）：2233—2240. （In Chinese）

[5] ? ?YU B，ZHOU H L，GAO Q，et al. Geometry boundary identification of the furnace inner wall by BEM without iteration[J]. Numerical Heat Transfer，2016，69（11）：1253—1262.

[6] ? ?YU B，YAO W A，GAO Q，et al. A novel non-iterative inverse method for estimating boundary condition of the furnace inner wall[J]. International Communications in Heat and Mass Transfer，2017，87：91—97.

[7] ? ?HUANG C H，YUAN I C，AY H. A three-dimensional inverse problem in imaging the local heat transfer coefficients for plate finned-tube heat exchangers[J]. International Journal of Heat and Mass Transfer，2003，46（19）：3629—3638.

[8] ? ?YANG K，JIANG G H，PENG H F，et al. A new modified Levenberg-Marquardt algorithm for identifying the temperature-dependent conductivity of solids based on the radial integration boundary element method[J]. International Journal of Heat and Mass Transfer，2019，144：118615.

[9] ? ?XIONG P，DENG J，LU T，et al. A sequential conjugate gradient method to estimate heat flux for nonlinear inverse heat conduction problem[J]. Annals of Nuclear Energy，2020，149：107798.

[10] ?王堃，王廣軍，陳紅，等. 穩態傳熱邊界溫度分布的正則化共軛梯度反演[J]. 中國電機工程學報，2013，33（17）：78—82.

WANG K，WANG G J，CHEN H，et al. Regularization conjugate gradient inverse for the temperature distribution of steady-state heat transfer boundary[J]. Proceedings of the CSEE，2013，33（17）：78—82. （In Chinese）

[11] ?ELEGBEDE C. Structural reliability assessment based on particles swarm optimization[J].Structural Safety，2005，27（2）：171—186.

[12] ?LEE K H，BAEK S W，KIM K W. Inverse radiation analysis using repulsive particle swarm optimization algorithm[J].International Journal of Heat and Mass Transfer，2008，51（11/12）：2772—2783.

[13] ?LIU F B. A modified genetic algorithm for solving the inverse heat transfer problem of estimating plan heat source[J]. International Journal of Heat and Mass Transfer，2008，51（15/16）：3745—3752.

[14] ?PARWANI A K，TALUKDAR P，SUBBARAO P M V. Simultaneous estimation of strength and position of a heat source in a participating medium using DE algorithm[J]. Journal of Quantitative Spectroscopy and Radiative Transfer，2013，127：130—139.

[15] ?ZADEH L A. Fuzzy sets[J]. Information and Control，1965，8（3）：338—353.

[16] ?WANG G J，LUO Z M，ZHU L N，et al. Fuzzy estimation for temperature distribution of furnace inner surface[J]. International Journal of Thermal Sciences，2012，51：84—90.

[17] ?LI Y H，WANG G J，CHEN H，et al. A decentralized fuzzy inference method for the inverse geometry heat conduction problem[J]. Applied Thermal Engineering，2016，106：109—116.

[18] ?WANG G J，ZHU L N，CHEN H. A decentralized fuzzy inference method for solving the two-dimensional steady inverse heat conduction problem of estimating boundary condition[J]. International Journal of Heat and Mass Transfer，2011，54（13/14）：2782—2788.

[19] ?KRZYWANSKI J，NOWAK W. Modeling of bed-to-wall heat transfer coefficient in a large-scale CFBC by fuzzy logic approach[J].International Journal of Heat and Mass Transfer，2016，94：327—334.

[20] ?CHEN T C，LEE M H. Intelligent fuzzy weighted input estimation method applied to inverse heat conduction problems[J]. International Journal of Heat and Mass Transfer，2008，51（17/18）：4168—4183.

[21] ?姜曙，朱震宇，萬世斌. 基于邊界元和分散式模糊推理的圓筒內壁形狀識別算法[J]. 世界科技研究與發展，2015，37（2）：122—126.

JIANG S，ZHU Z Y，WAN S B. Geometry estimation of furnace inner wall based on BEM and decentralized fuzzy inference method[J]. World Sci-Tech R & D，2015，37（2）：122—126. （In Chinese）

收稿日期：2021-01-19

基金項目：國家重點研發計劃資助項目（2018YFB0104501），National Key Research and Development Program of China（2018YFB0104501）

作者簡介：雷飛（1981—），男，河南淅川人，湖南大學副教授，博士

通信聯系人，E-mail：fea_lei@163.com