Exact analytical propagators for anisotropic quantum dots under magnetic field with atomic spin-orbital coupling

CHEN Yin, GUO Wei, PAN Xiaoyin

Exact analytical propagators for anisotropic quantum dots under magnetic field with atomic spin-orbital coupling

CHEN Yin, GUO Wei, PAN Xiaoyin*

( School of Physical Science and Technology, Ningbo University, Ningbo 315211, China )

In quantum mechanics, there are very few systems whose propagators can be obtained exactly, especially in the case of taking spin-orbital coupling (SOC) effects into account. Using the group theoretical method in phase space, we start with deriving exact analytical expressions for the propagators of anisotropic quantum dots with atomic spin-orbital coupling (ASOC). As an example of application, the evolution of spin-dependent Gaussian wave packets is calculated using the propagator, along with which the corresponding probability densities, the effects of ASOC and magnetic field on the expectations of the distances are also investigated.

path-integral method; spin-orbital coupling; quantum dot; magnetic field

1 Introduction

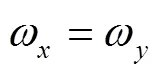
However, because the presence of asymmetry in the confining potential is experimentally more realistic, there exist lots of works on the anisotropic QDs with the broken rotational symmetry, thereby altered electronic and dynamical properties[3,16-20]. In order to study the magnetic properties of such QDs, the FD model has also been generalized to the elliptical parabolic potential case and been solved exactly[21]. Consequently, various physicalproperties, such as the quantization of the conductance[22]and the electronic properties, can be studied[23]. Moreover, this model also can be used to study rotating droplets of electrons trapped in quasi-two-dimensional quantum dots and rotating Bose-Einstein condensates[24].

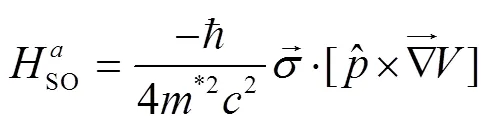
Hence, it will be interesting to understand the spin- dependent evolution of wave packets for electrons confined in quantum dots under a perpendicular magnetic field with ASOC. In order to get a better handle on the evolution of the corresponding physical systems, the propagator method[31-32]is regarded as a powerful tool and shall be a good choice. It is well known in quantum mechanics that the propagator as a Green’s function of the Schr?dinger equation contains all the information about the system and plays a central role in Feynman’s path integral approach[31-32]to solve non-relativistic quantum mechanical problems. However, due to the difficulty of obtaining the analytical expressions for the propagators, to our knowledge there are very few such investigations and are solely limited to the isotropic cases[33]. To study the more interesting anisotropic case with broken rotational symmetry, in the present work we derive analytical expressions for the propagator of such systems using the group theoretical method on phase space[34], then the effects of the ASOC and magnetic field on the evolution of the spin-dependent wave packets and the expectations of distances for spin-up and down components are investigated as an example of application.

2 The Hamiltonian

Consider a 2D system of an electron of charge= -,>0 and effective mass*confined in an anisotropic QD, under a perpendicular constant magnetic fieldalong the-direction. Then the Hamiltonian takes the form,

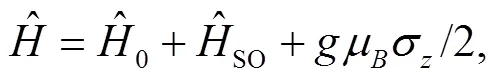
where

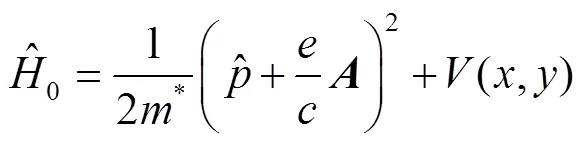
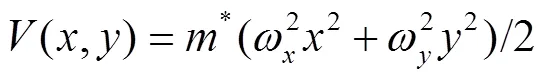
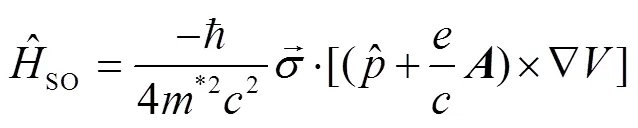
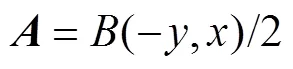
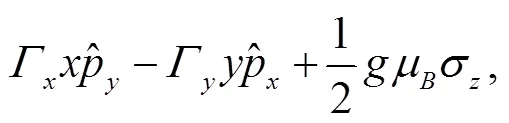
where the coefficients are matrices,

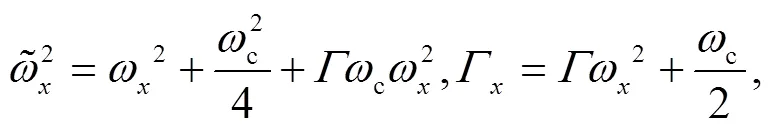
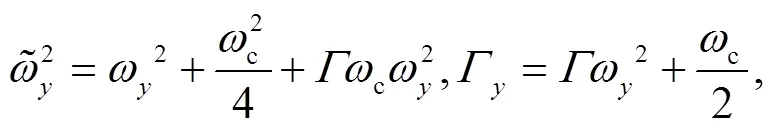
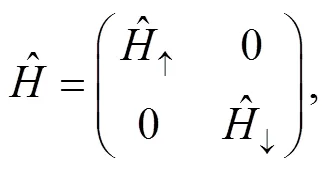
3 Calculations of the exact analytical propagator

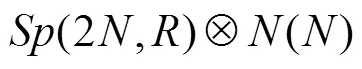
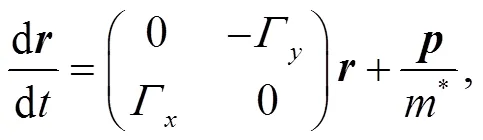
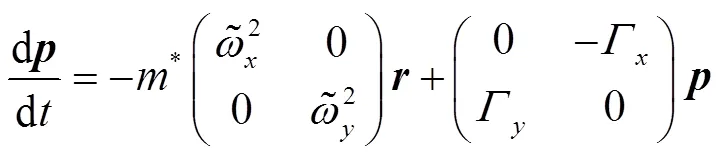
or in matrix form as

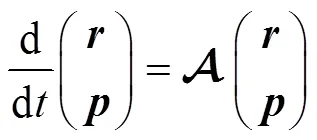
where the matrix

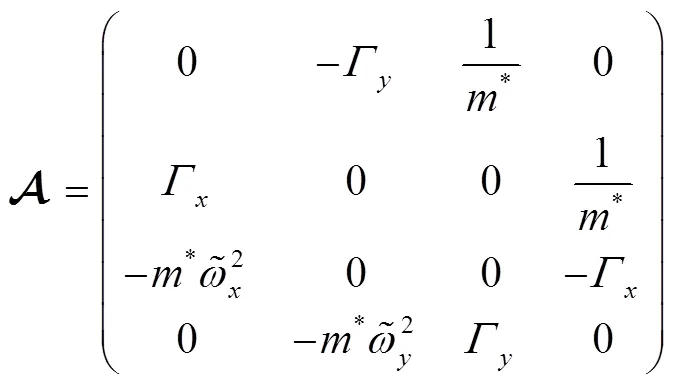
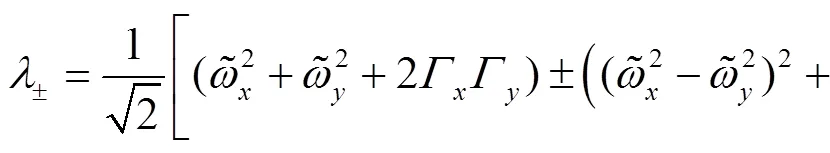
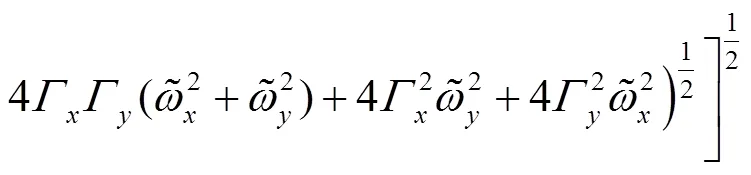
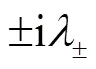
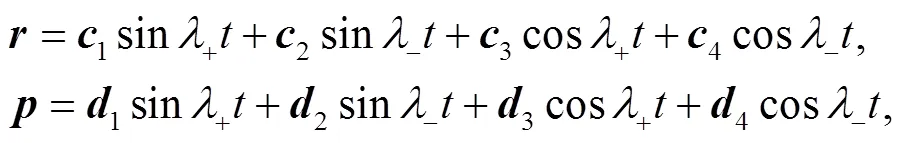
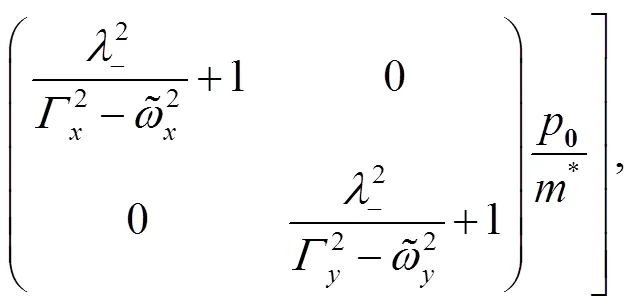
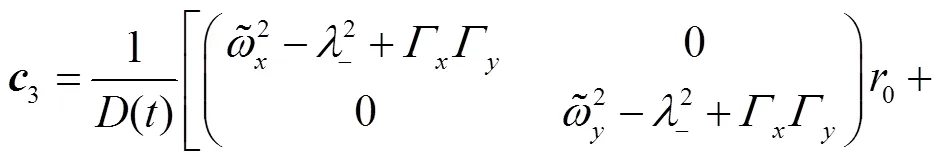
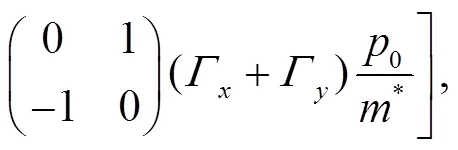
and

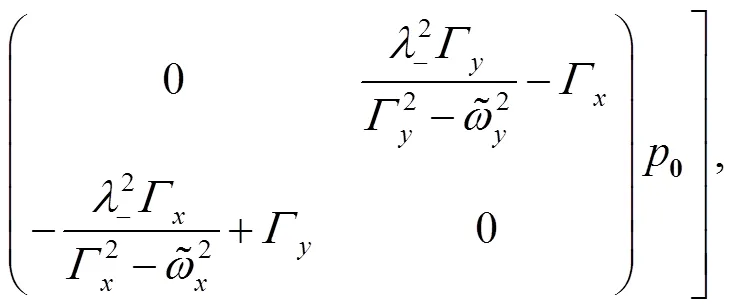
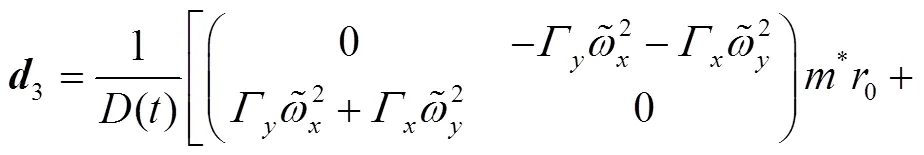
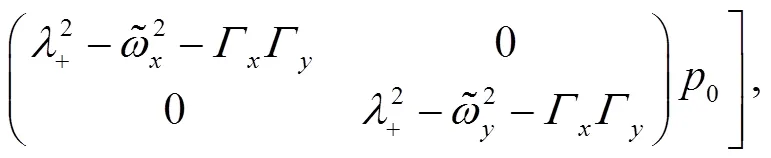
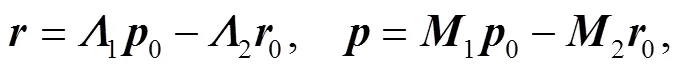
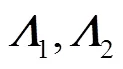
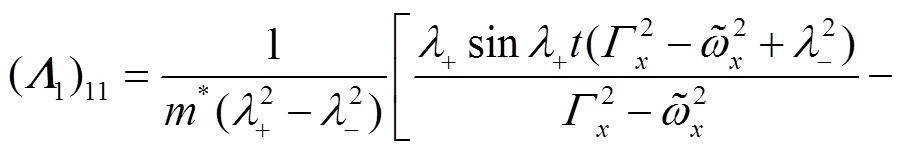
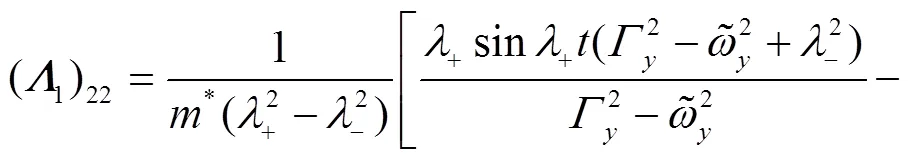
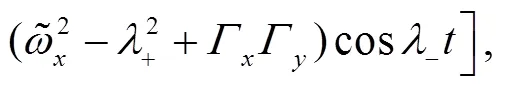
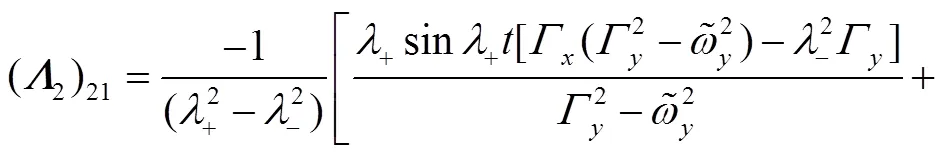
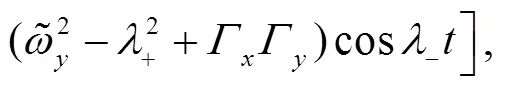
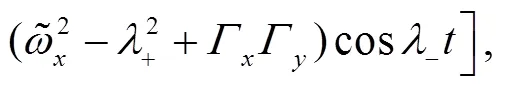
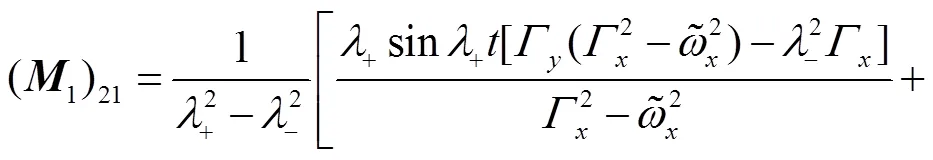
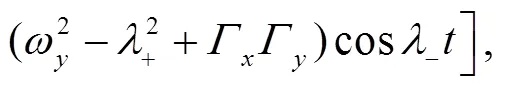
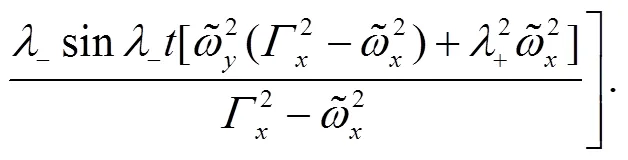
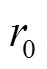
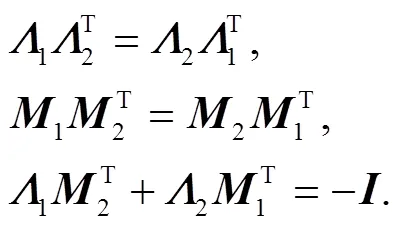
These identities shall be useful later on.

Having obtained the solutions for EOM, we can obtain the propagator directly by the group theoretical method on phase space[34],

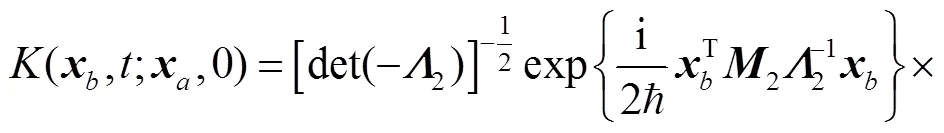
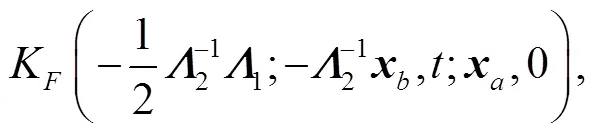
where the second term on the r. h. s of above equation is defined as

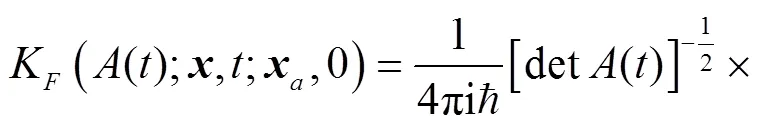
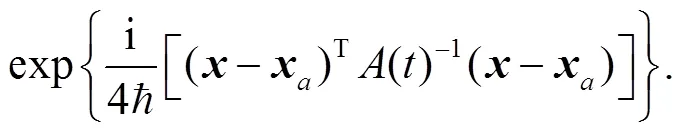
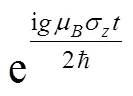
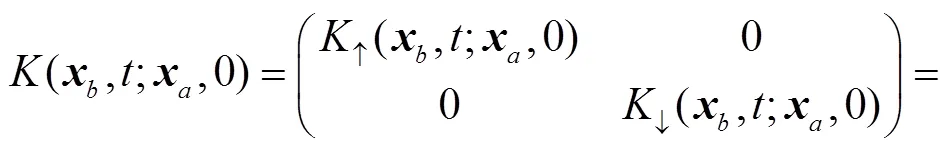
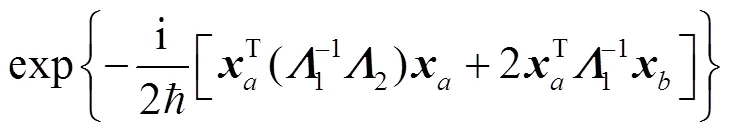
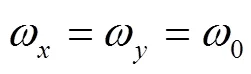
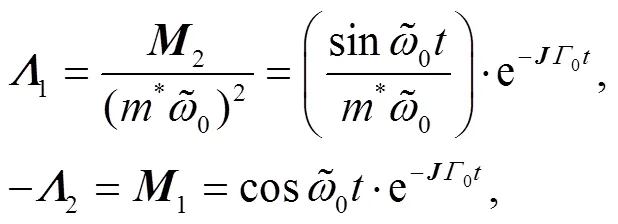
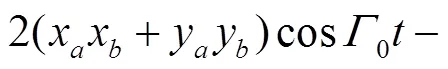
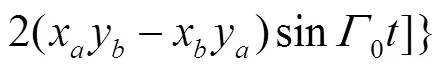
4 The ASOC effects on the evolution of spin-dependent wave packets

As an example of application, next let us consider the evolution of a 2D Gaussian wave packet that has the following form initially at=0,

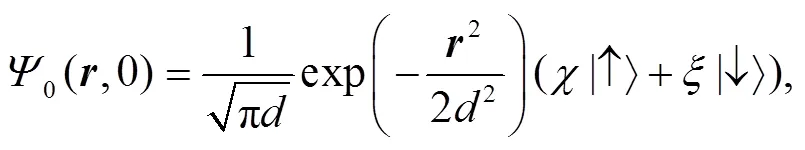
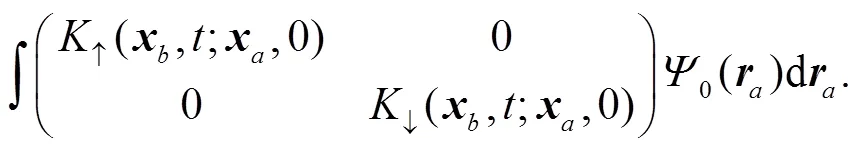
Inserting the expression for the propagator into above equation, and performing the integral we obtain

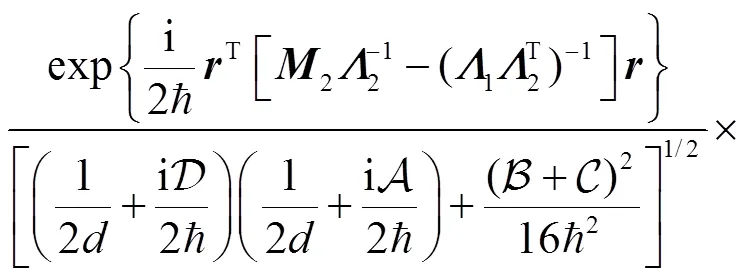
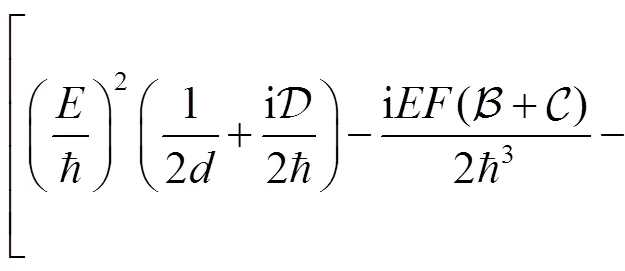
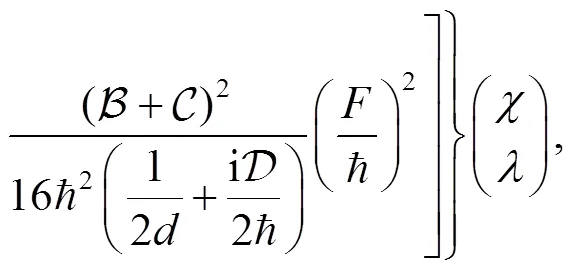
where,are functions of (,), i.e.,

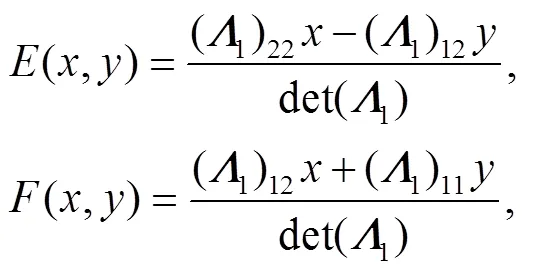
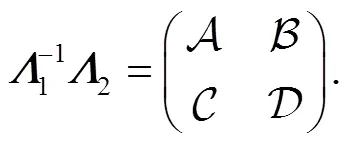
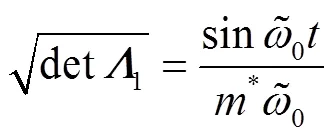
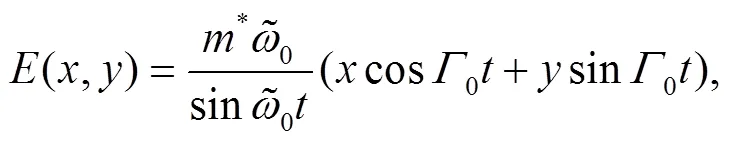
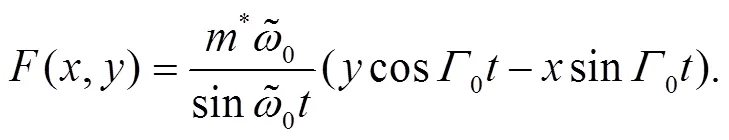
Thus, Eq. (28) reduces to

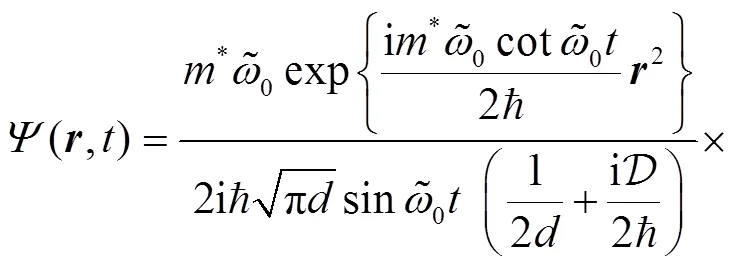
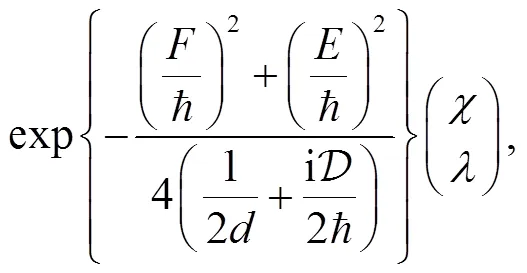
and the spatial density is

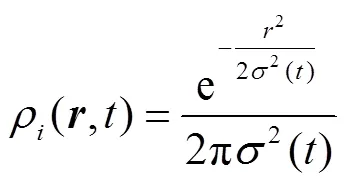
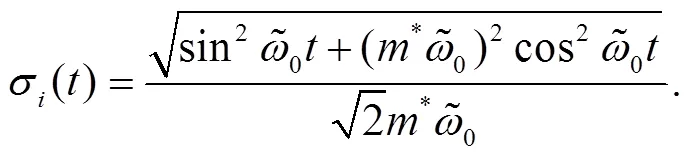
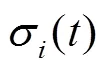
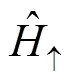
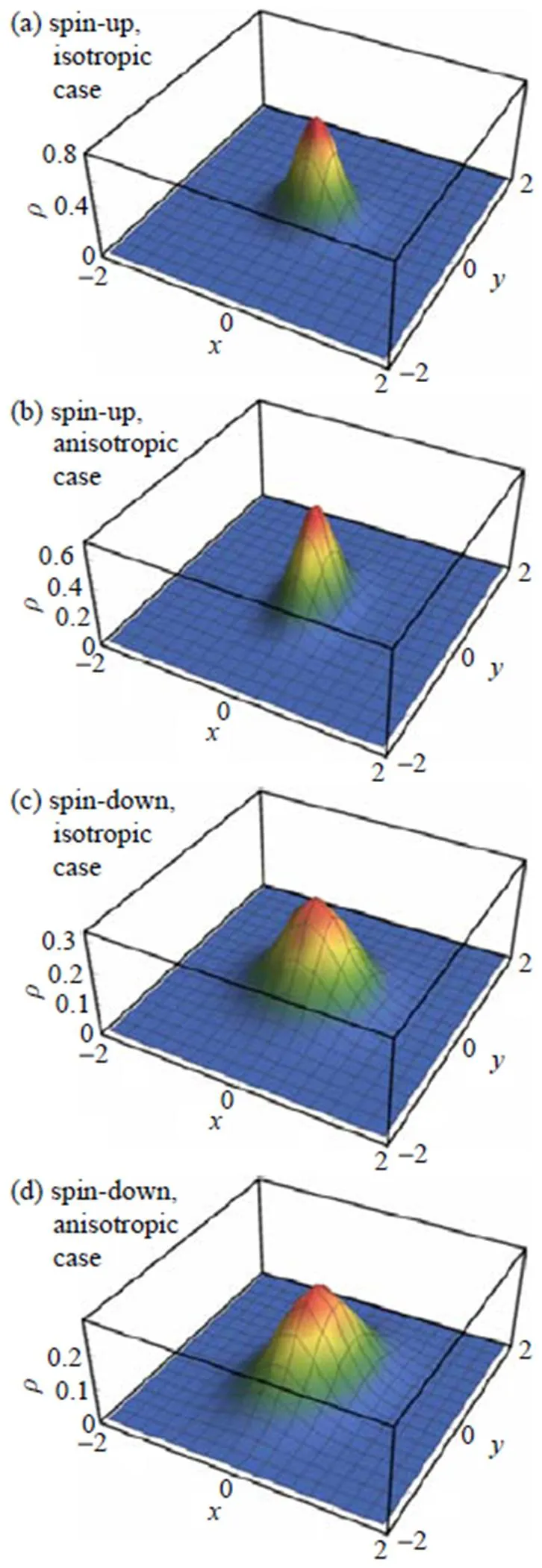
Fig. 1 The probability densities for the QD with |Γ|=0.25

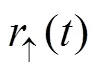
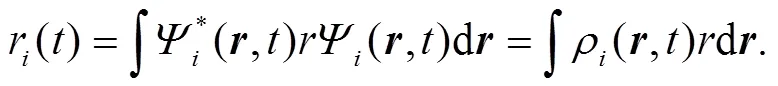
In the isotropic cases, the substitution of Eq. (33) into (35) yields the following analytical expression,

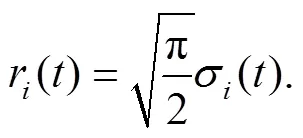
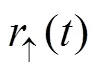
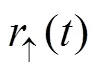
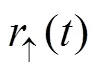
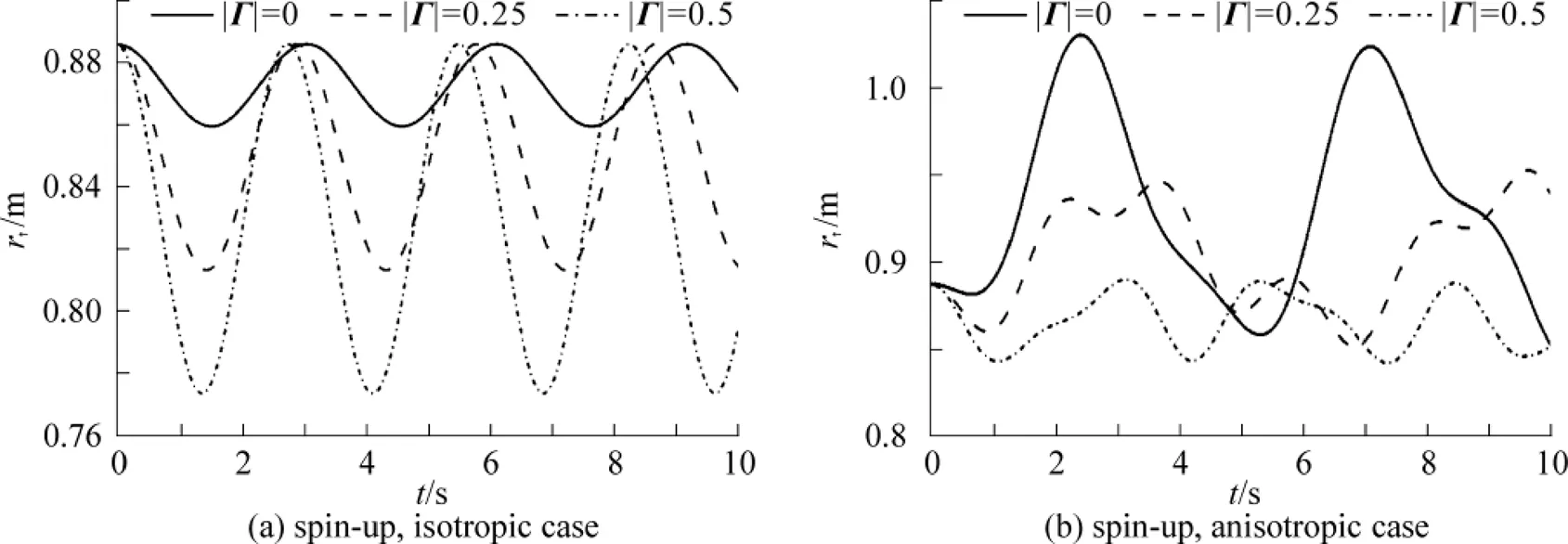
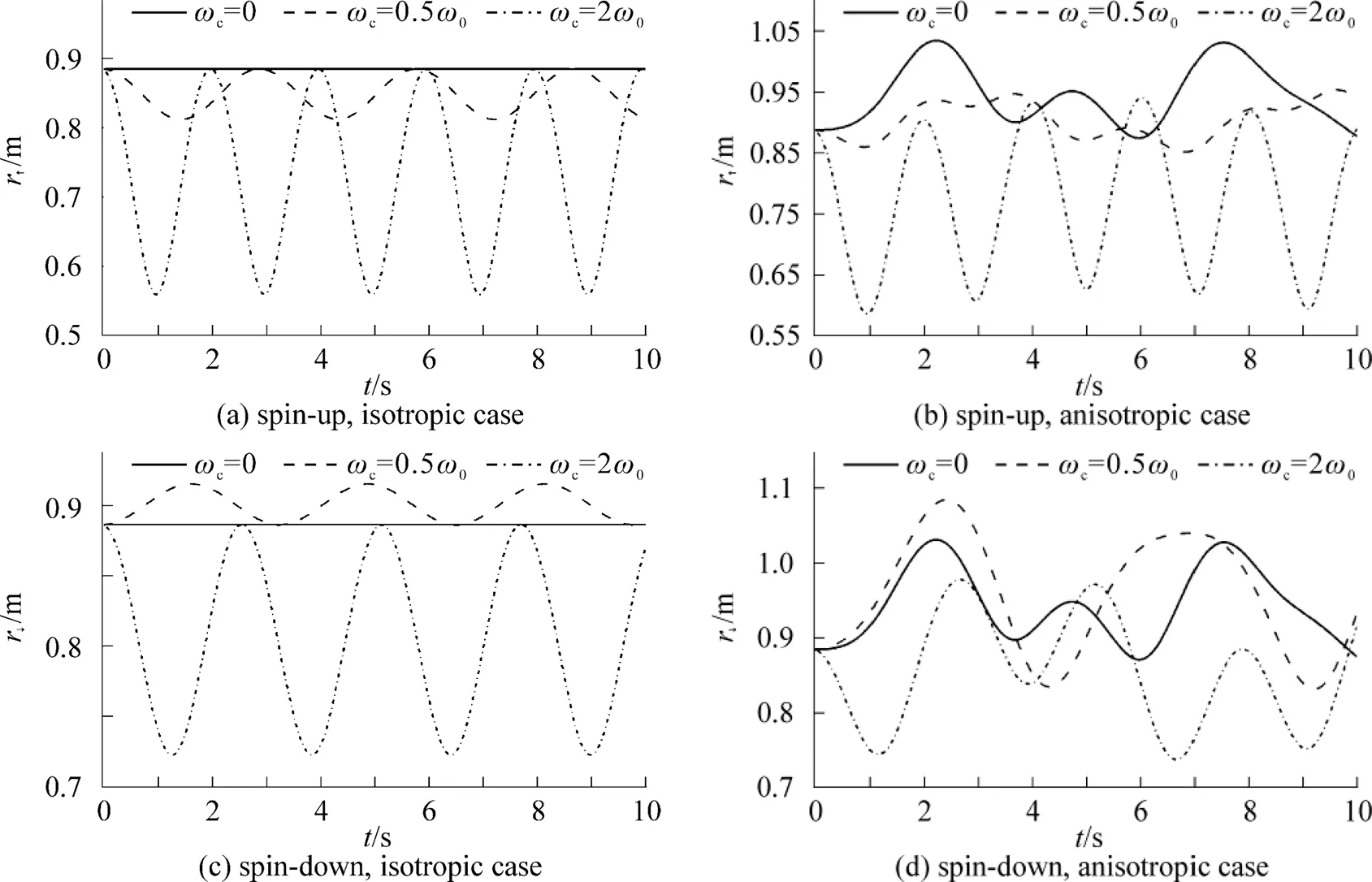
Fig. 3 and for the quantum dot at fixed strength of the ASOC |Γ|= 0.25

5 Conclusions

By employing the group theoretical method, we have obtained analytical expressions for the propagators of anisotropic quantum dots with atomic SOC, then as an example of application, the propagator is applied to calculate the evolution of spin-dependent Gaussian wave packets. Consequently, the corresponding probability densities, expectations of the distances are investigated for the anisotropic and isotropic cases. The wave packet splits into two components, one for spin-up and the other for spin-down, and they evolve differently. It is shown that in the isotropic cases, a Gaussian wave packet is always a Gaussian and the cylinder symmetry of the probability densities is kept all the time, and the expectations of the distances are periodic functions of time. While in the anisotropic case, this symmetry of the probability densities is broken and the expectations of the distances become quasi-periodic functions of time. Nevertheless, the strength of the ASOC and the magnetic field in the anisotropic case have similar effects on the averages of the expectations of the distances to those in the isotropic case. But their effects on spin-up component are quite different from those on spin-down one. It must be stressed that this group- theoretical method relies on the solutions to the quite complicated equation of motion of the system, and this may not be achieved for other forms of SOC like Rashba SOC or Dresselhaus SOC. Finally, it is worthy to mention that the propagator we obtained may also be applied to study the evolution of spin-dependent atomic wave packets in a harmonic magnetic trapping potential in the area of Bose-Einstein condensates[36-37].

[1] Chakraborty T. Quantum Dots[M]. Amsterdam: Elsevier, 1999.

[2] Jack L, Harylak P, Wojs A. Quantum Dots[M]. Heidelberg: Springer-Verlag, 2013.

[3] Reimann S M, Manninen M. Electronic structure of quantum dots[J]. Reviews of Modern Physics, 2002, 74(4):1283-1342.

[4] Hanson R, Kouwenhoven L P, Petta J R, et al. Spins in few-electron quantum dots[J]. Reviews of Modern Physics, 2007, 79(4):1217-1265.

[5] Birman J L, Nazmitdinov R G, Yukalov V I. Effects of symmetry breaking infinite quantum systems[J]. Physics Reports, 2013, 526(1):1-91.

[6] Bogachek E N, Landman U. Edge states, Aharonov- Bohm oscillations, and thermodynamic and spectral properties in a two-dimensional electron gas with an antidot[J]. Physical Review B, 1995, 52:14067-14077.

[7] Hornberger K, Smilansky U. Magnetic edge states[J]. Physics Reports, 2002, 367(4):249-385.

[8] Matulis A, Pyragien? T. Magnetic edge states of an impenetrable stripe[J]. Physical Review B, 2003, 67(4): 045318.

[9] Harrison P, Valavanis A. Quantum wells, wires and dots: theoretical and computational physics of semiconductor nanostructures[M]. Hoboken, NJ: John Wiley & Sons, Inc, 2016.

[10] Viefers S, Koskinen P, Singha Deo P, et al. Quantum rings for beginners: energy spectra and persistent currents[J]. Physica E: Low-dimensional Systems and Nanostructures, 2004, 21(1):1-35.

[11] Fock V. Bemerkung zur quantelung des harmonischen oszillators im magnetfeld[J]. Zeitschrift fur Physik, 1928, 47(5/6):446-448.

[12] Darwin C G. The diamagnetism of the free electron[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1931, 27(1):86-90.

[13] MacDonald A H. Quantum Hall Effect: A Perspective[M]. Dordrecht: Springer Netherlands, 1989.

[14] Chakraborty T, Pietil?inen P. The Fractional Quantum Hall Effect[M]. Heidelberg: Springer, 1988.

[15] Prange R E, Girvin S M. The Quantum Hall Effect[M]. New York: Springer-Verlag, 1990.

[16] Tarucha S, Austing D G, Sasaki S, et al. Effects of Coulomb interactions on spin states in vertical semiconductor quantum dots[J]. Applied Physics A: Materials Science & Processing, 2000, 71(4):367-378.

[17] Maksym P. Quantum states of interacting electrons in a 2D elliptical quantum dot[J]. Physica B: Condensed Matter, 1998, 249/250/251:233-237.

[18] Ezaki T, Mori N, Hamaguchi C. Electronic structures in circular, elliptic, and triangular quantum dots[J]. Physical Review B, 1997, 56(11):6428-6431.

[19] Fujito M, Natori A, Yasunaga H. Many-electron ground states in anisotropic parabolic quantum dots[J]. Physical Review B, 1996, 53(15):9952-9958.

[20] Hirose K, Wingreen N S. Spin-density-functional theory of circular and elliptical quantum dots[J]. Physical Review B, 1999, 59:4604-4607.

[21] Schuh B. Algebraic solution of a non-trivial oscillator problem[J]. Journal of Physics A: Mathematical and General, 1985, 18:803-807.

[22] Madhav A V, Chakraborty T. Electronic properties of anisotropic quantum dots in a magnetic field[J]. Physical Review B, 1994, 49:8163-8168.

[23] Geyler V A, Margulis V A. Quantization of the conductance of a three-dimensional quantum wire in the presence of a magnetic field[J]. Physical Review B, 2000, 61:1716-1719.

[24] Saarikoski H, Reimann S M, Harju A, et al. Vortices in quantum droplets: Analogies between boson and fermion systems[J]. Reviews of Modern Physics, 2010, 82:2785- 2834.

[25] Bandyopadhyay S. Introduction to Spintronics[M]. Boca Rota, FL: CRC Press, 2008.

[26] Rashba E I. Properties of semiconductors with an extremum loop. I. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop[J]. Soviet physics - Solid state, 1960, 2:1109- 1131.

[27] Bychkov Y A, Rashba E I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers[J]. Journal of Physics C: Solid State Physics, 1984, 17:6039-6045.

[28] Kato Y K, Myers R C, Gossard A C, et al. Observation of the spin Hall effect in semiconductors[J]. Science, 2004, 306(5703):1910-1913.

[29] Sinova J, Culcer D, Niu Q, et al. Universal intrinsic spin Hall effect[J]. Physical Review Letters, 2004, 92:126603.

[30] Dresselhaus G. Spin-orbit coupling effects in zinc-blende structures[J]. Physical Review, 1955, 100:580-586.

[31] Feynman R P. Space-time approach to non-relativistic quantum mechanics[J]. Reviews of Modern Physics, 1948, 20:367-387.

[32] Feynman R P, Hibbs A R. Quantum Mechanics and Path Integrals[M]. New York: McGraw-Hill, 1965.

[33] Hsu B C,van Huele J F S. Analytic propagators for spin-orbit interactions[J]. Journal of Physics A: Mathematical and Theoretical, 2009, 42:475304.

[34] Howard S D, Roy S K. Group theoretical techniques on phase space and the calculation of quantum mechanical propagators[J]. Journal of Physics A: Mathematical and General, 1989, 22:4865-4876.

[35] Bernevig B A, Zhang S C. Quantum spin Hall effect[J]. Physical Review Letters, 2006, 96:106802.

[36] Wen L H, Liu M, Xiong H W, et al. Interference of Bose-Einstein condensates and entangled single-atom state in a spin-dependent optical lattice[J]. The European Physical Journal D, 2005, 36(1):89-94.

[37] Wen L H, Liu M, Kong L B, et al. Evolution of spin-dependent atomic wave packets in a harmonic potential[J]. Chinese Physics, 2005, 14(4):690-696.

磁場下有原子自旋軌道耦合的各向異性量子點的精確解析傳播子

陳 寅, 郭 偉, 潘孝胤*

（寧波大學 物理科學與技術學院, 浙江 寧波 315211）

量子力學中很少有系統能夠精確地計算傳播子, 特別是在考慮了自旋軌道耦合效應的情況下. 利用相空間的群論方法, 首先導出了有原子自旋軌道耦合的各向異性量子點傳播子的精確解析表達式. 隨后利用傳播子來計算自旋高斯波包的演化與相應的概率密度, 并研究了原子自旋軌道耦合效應和磁場強度對距離期望值的影響.

路徑積分方法; 自旋軌道耦合; 量子點; 磁場

2020?08?01.

寧波大學學報（理工版）網址: http://journallg.nbu.edu.cn/

國家自然科學基金（11375090）.

陳寅（1990－）, 男, 浙江寧海人, 在讀碩士研究生, 主要研究方向: 量子器件相關理論計算. E-mail: 15336698809@163.com

潘孝胤（1974－）, 男, 浙江寧海人, 研究員, 主要研究方向: 凝聚態理論. E-mail: panxiaoyin@nbu.edu.cn

O413.1

A

1001-5132（2021）01-0055-10

（責任編輯 韓 超）