含水合物地層井壁力學狀態的彈塑性解析分析

王華寧，郭振宇，高 翔，蔣明鏡

（1.同濟大學航空航天與力學學院，上海200092；2.同濟大學土木工程防災國家重點實驗室，上海200092；3.天津大學建筑工程學院，天津300350）

天然氣水合物是一種分布范圍廣、儲量豐富的新型清潔能源，目前發現的天然氣水合物超過90%存在于海底沉積物中［1］。包括中國在內的多個國家已提出水合物開采計劃并進行了開采試驗。由于鉆井和開采過程中環境和邊界條件改變造成的水合物分解和井周土體力學性能劣化，在多國試采中均出現過生產井周土層的垮塌失穩等事故［2-3］。井壁垮塌、破裂、縮徑等現象稱為井壁失穩，是水合物開采所面臨的主要問題之一［2-4］。水合物分解造成土體力學特性劣化是影響井壁穩定的關鍵因素，該過程涉及溫度場、滲流場等多個物理場與力場的相互作用。目前，針對水合物地層井壁穩定問題的研究多采用數值模擬的方法。Li等［5］利用數值方法研究了水合物儲層的深度、分解范圍和分解后的力學性能對井壁縱向沉降的影響。寧伏龍等［6］考慮了鉆井液特性對其侵入地層的影響，通過一維數值模型研究過壓鉆井條件下的井壁安全問題。Sun等［7］建立了數值模型研究鉆井液特性、儲層的滲透率及飽和度對井壁力學狀態的影響，并基于Mohr-Coulomb（MC）準則考慮了地層的屈服。相比之下，將關鍵因素抽象簡化后得到的解析解答能夠高效地進行參數分析，并可分析參數在解答中的作用，進行力學機理的探究。本文將建立解析模型，研究深海含水合物地層中井壁穩定問題。

傳統井壁、隧道/巷道力學分析的解析研究多針對彈/黏彈性［8-9］、彈塑性問題展開［10-16］。目前針對彈塑性模型的研究，一般考慮各向等壓圓形孔洞的受力問題（軸對稱問題）［10］。彈塑性問題的解答通常基于 M-C［11］、Hoek-Brown［12］屈服準則和統一強度理論［13］等，以及理想塑［14］、彈脆塑［15］和考慮非線性軟化［16］等本構關系得到力場的解析或半解析解答。上述研究主要針對孔洞周邊為單一巖土材料，部分解答中考慮滲流場對力場的影響。水合物井壁穩定問題的特殊性和復雜性主要在于①由于水合物對環境溫度和壓力的改變非常敏感，在鉆井過程中水合物可能發生分解，而分解造成微觀結構的變化（例如孔隙率變大）也影響溫壓分布；②水合物分解對土體力學特性影響顯著，導致井壁承載能力下降，必須在計算物理場和力場時區分對待分解和未分解域；③溫度和滲流場對力場存在多種影響。在凍結法施工［17］中凍結壁分析、支護隧道分析［18］［19］等屬于多域問題，但并未涉及溫度和滲流的共同作用，或是基于彈性本構的計算，且結構本身的尺度和特性與水合物地層中井壁問題有很大區別。Wang等［20］考慮上述多場關系，建立了水合物地層井壁穩定的彈性模型，并通過屈服準則進行井壁穩定的初步分析。

本文對實際問題進行合理簡化，考慮水合物分解對地層滲透、導熱和力學特性的影響，以及滲流場對力場的作用，基于M-C準則和理想彈塑性模型，推導了水合物地層中井周應力和位移的彈塑性解答，并利用解析模型對井壁的穩定性進行分析。

1 力學模型

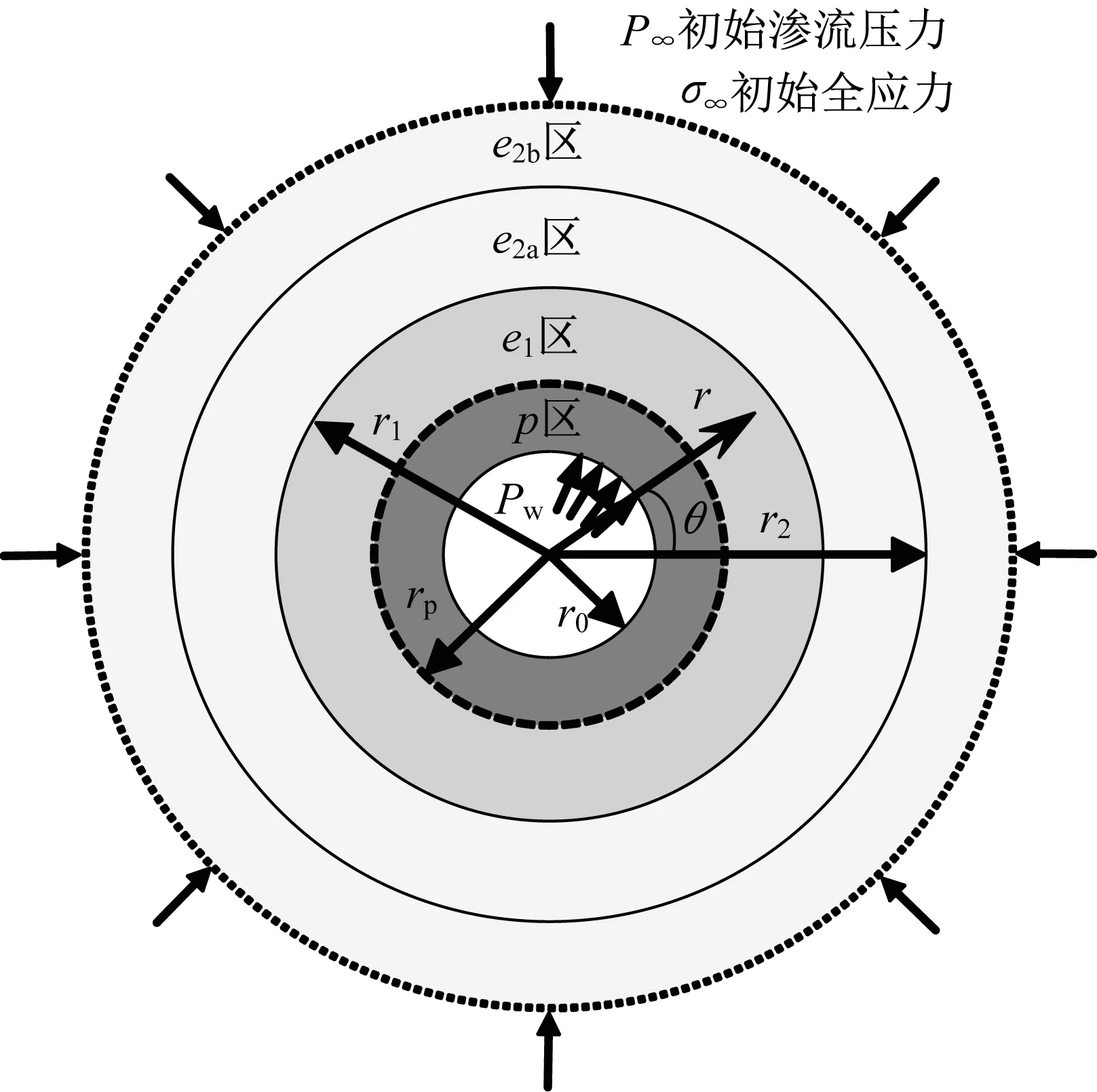
圖1 水合物地層中井壁穩定力學模型Fig.1 Mechanicalmodelforwellboredrillingin methane hydrate-bearing sediments

本文主要研究含水合物地層鉆井過程中，在井口橫截面內由于過大的應力/位移而導致的井壁失穩問題，未涉及井壁縱向失穩和開采過程中出砂淤堵等其他失穩方式。由于井軸向尺寸遠大于井口半徑，且儲層所處地應力較大，可忽略豎向重力梯度影響，因此簡化為水平截面內平面應變問題。有研究顯示，面內兩方向初始應力可認為近似相等［21］；上下有不透水層，假定溫度和滲流場也僅與徑向位置相關，為軸對稱問題。與傳統問題不同的是，鉆井引起的井周溫度和滲流壓力的改變導致一定區域內水合物分解，從而引起分解域土體參數改變，因此水合物井壁為多域問題。本文關注時間較大時刻的穩態問題，此時對應的力場最危險。根據以上簡化，幾何模型和受力情況見圖1，由內到外依次為：p區（r0≤r≤rp）：分解域塑性區；e1區（rp＜r≤r1）：分解域彈性區；e2a區（r1＜r≤r2）：未分解域彈性區（有溫壓變化）；e2b區（r＞r2）：無窮域（溫壓保持原始值）。在p區和e1區將考慮水合物分解對熱量和壓力傳遞參量以及力學參數（彈性模量和黏聚力）的影響。根據試采和數值分析結果［6］發現鉆井引發的溫度和壓力的改變僅在井壁有限范圍內，因此設置e2a區，其中r2為溫壓影響的最大半徑。而最外側的e2b區內的溫度和壓力未受到鉆井影響，均為原始值。圖中Pw為鉆井液壓力，總應力σ∞作用在無窮遠處。推導中多場相互影響關系見圖2。考慮滲流壓力對儲層有效應力的影響，未考慮應力場對滲流場和溫度場的影響；地層假定為滿足M-C準則的理想彈塑性模型。由于鉆井過程分解域較小，為簡化求解，忽略分解域和未分解域之間過渡區域的影響，并且僅考慮塑性區在分解域內的最常見情況（rp＜r1）。

2 溫度場/滲流壓力場解答

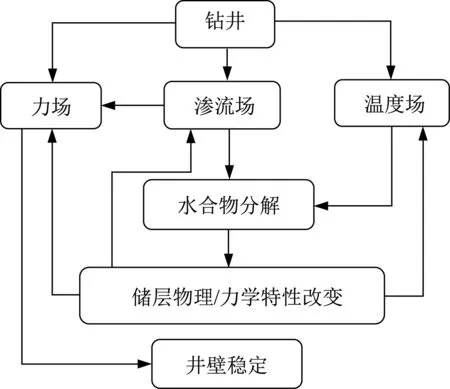
圖2 力場、滲流場和溫度場的耦合關系Fig.2 Coupling relationship between mechanics,seepage and temperature field

鉆井引發井周溫度和孔隙壓力變化，導致一定范圍內水合物發生分解，并使地層導熱和滲透系數變化，引起滲流場和力場的進一步改變。由于該階段分解域較小，且考慮時間足夠長的穩態問題，因此忽略水合物分解產生的水氣及熱量變化的影響。本節給出溫度場和滲流壓力場的解析表達式，并確定分解域范圍。

2.1 溫度場

根據假定，本問題為穩態軸對稱溫度分布。考慮熱傳導的熱量傳遞方式，存在的熱對流形式通過增大分解域內的導熱系數近似考慮［22］。穩態熱傳導問題的控制方程和定解條件為（軸對稱）：

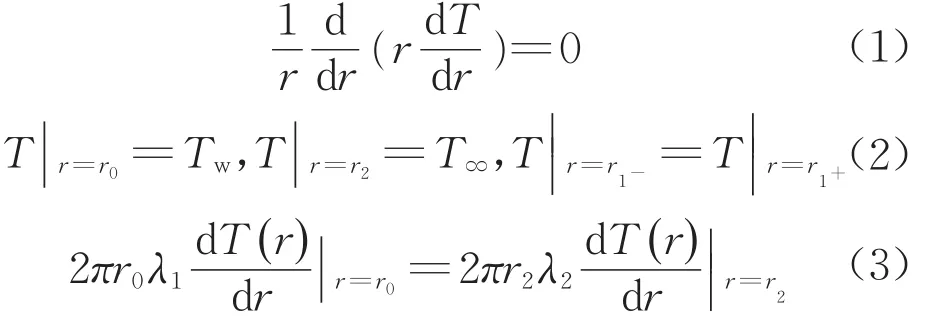
式中，Tw表示鉆井液溫度，T∞表示儲層初始溫度，λ1和λ2分別表示分解域和未分解域的熱傳導系數。無窮域內（r≥r2）溫度保持在初始值。求解式（1）得到含有待定系數的通解，得

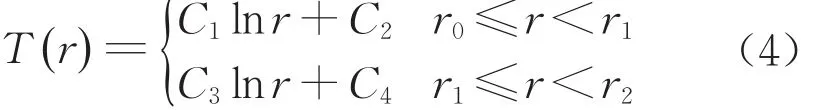
將式（4）代入式（2）～式（3）中可確定待定系數C1～C4，最終得到溫度場

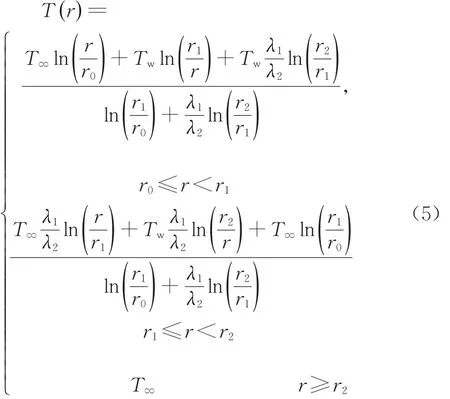
2.2 滲流壓力場

認為孔隙中流體流動滿足達西定律，穩態滲流場的控制方程和定解條件為

式中，k1和k2分別表示分解域和未分解域的滲透系數。與溫度場的數學求解過程相似，由式（6）～（8）可確定孔隙壓力分布規律為

與未考慮分解域的單域問題不同，上式中溫度/壓力場均與分解域的相對熱傳導系數（λ1/λ2）和相對滲透系數（k1/k2）相關。

2.3 分解域的確定

水合物的相平衡方程可通過海水中純水合物的相平衡試驗數據［23］擬合得

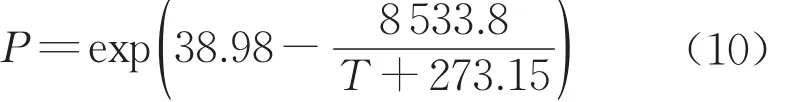
式中：P的單位為kPa；T的單位為oC。在r=r1處溫度與壓力應恰好滿足上述關系，在分解域內，實際滲流壓力小于上式的計算值。將T(r1)和P(r1)代入式（10）可求解分解域半徑r1。

3 應力和位移場解答

當鉆井液壓力在一定范圍內時，井壁全域處于彈性階段，當鉆壓過小或者過大時，井壁將進入塑性［20］。本節將推導彈性階段和塑性階段應力及位移場的解析表達式。規定壓應力為正，位移朝向井眼為正。

3.1 力學模型與基本方程

試驗結果顯示，在較高的圍壓下含水合物土體進入塑性階段后，沒有出現明顯的應變軟化或硬化［24］，因此本文采用理想彈塑性模型模擬水合物地層。井壁附近水合物的分解引起分解域彈性模量和黏聚力發生變化，即

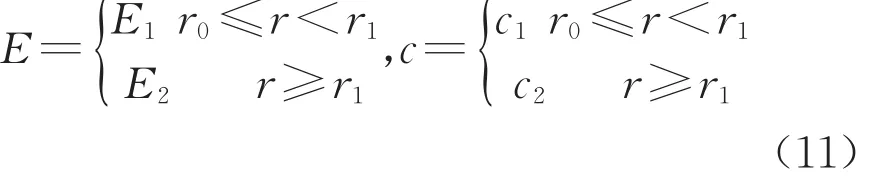
式中：E1和c1表示分解域的彈性模量和黏聚力；E2和c2表示水合物地層的原始彈性模量和黏聚力，均為常數。水合物分解對儲層泊松比（ν）和內摩擦角（φ）影響很小，可以忽略［25］。

極坐標系下的平衡方程為

式中：σri和σθi表示徑向和環向正應力（有效應力），α為有效應力系數。幾何方程為

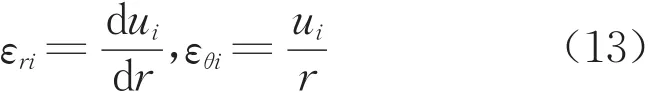
式中：εri和 εθi表示徑向和環向應變；ui表示徑向位移。上標i=p，e1，e2a，e2b分別表示塑性區以及三個彈性區中的變量。

彈性區有效應力與應變關系滿足胡克定律：

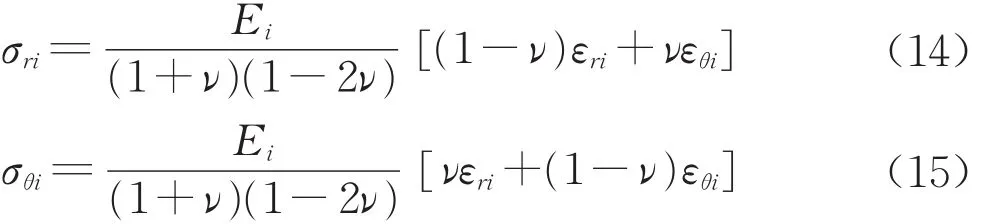
式 中 ：i=e1，e2a，e2b，彈 性 模 量 滿 足認為地層滿足Mohr-Coulomb屈服準則，用主應力表示的屈服準則為

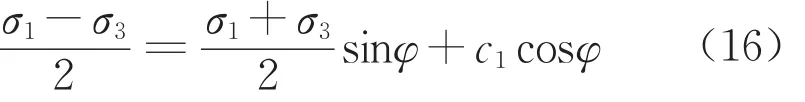
塑性應變滿足非關聯的流動法則為

式中：εrpa和εθpa表示塑性區的徑向和環向塑性應變，當徑向應力為第一主應力時，β=(1-sinψ)/(1+sinψ)，當環向應力為第一主應力時，β=(1+sinψ)/(1-sinψ)，ψ表示剪脹角。

以上是本文解析模型涉及的基本方程。此外，模型需要滿足邊界條件和連續性條件。井壁和無窮遠處的邊界條件（有效應力）為

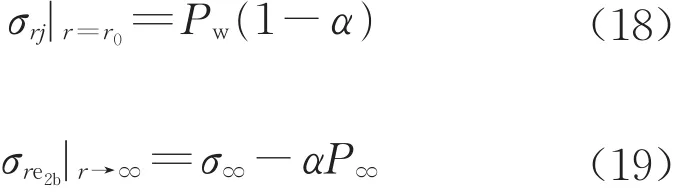
對于彈性問題j=e1，對于彈塑性問題j=p。相鄰區域在交界面處的應力和位移協調條件包括：

井壁穩定問題關注的是全部有效應力（初始應力和鉆井引發的增量應力之和）和鉆井引起的增量位移。圖3a為增量問題的計算模型，可通過圖3b給出的全量模型減去圖3c模型得到。其中σef1=σ∞-αP∞為無窮遠處初始有效應力；σef2=Pw(1-α)為井周鉆井液壓力提供的有效應力。根據上述模型的關系，應力有如下疊加關系，即

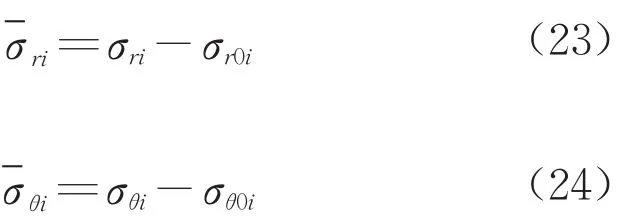
式中：i=p，e1，e2a，e2b。和表示增量應力（圖3a）；σri和 σθi表示全量應力（圖3b）；σr0i和σθ0i表示圖3c所示彈性模型的應力。三個模型彈性區的應力和位移都各自滿足式（12）～式（15）的基本方程，圖3b塑性區有效應力滿足屈服準則。

3.2 彈性階段應力/位移

首先求解圖3c所示模型的應力與位移。由于鉆井前地層孔隙壓力為常數（P∞），e2a和e2b區可以合并為一個e2區。此時全域處于彈性階段，將式（13）代入式（14）～（15），得到應力與位移的關系式，再將應力表達式代入式（12）得到關于位移的微分方程為

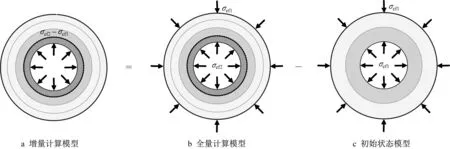
圖3 應力與增量位移計算Fig.3 Models for stress and incremental displacement calculation

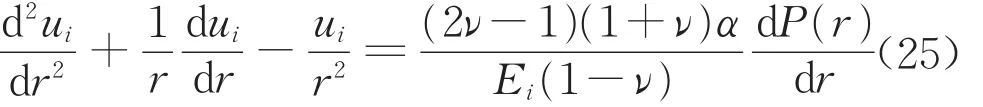
此時dP(r)/dr=0，求解該微分方程可得到i區（i=e1，e2）的位移表達式，再代回到式（14）～式（15），可得到相應的應力表達式，結果如下所示：

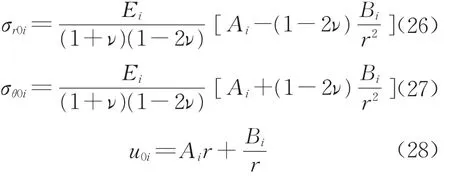
式中：Ai，Bi為待定系數。由邊界條件σr0e1|r=r0=σr0e2|r→∞=σef1=σ∞-αP∞以及分區交界面r=r1處的連續性條件σr0e1|r=r1=σr0e2|r=r1，u0e1|r=r1=u0e2|r=r1可求解系數Ai，Bi，并得到σr0i，σθ0i和u0i的解答。

下面求解彈性階段井壁的全量應力及增量位移，共有三個分區（e1、e2a、e2b）。與推導式（26）～式（28）的過程相似，通過聯立式（12）～式（15），可得各分區位移的微分方程，求解后得到含有待定系數的表達式。

當i=e1，e2a時，dP(r)/dr≠0，應力及位移表達式為

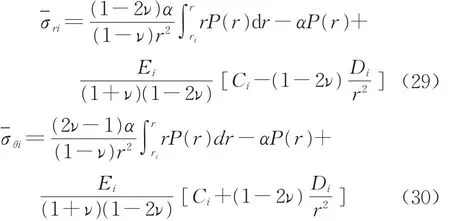
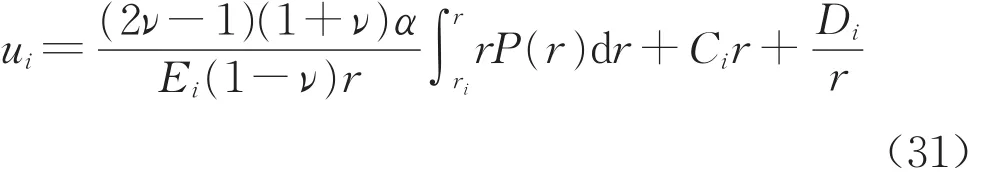
式中：Ci，Di為待定系數，積分下限re1=rp，re2a=r1。

無窮域（i=e2b）內的孔壓為常數，因此應力和位移的表達式在形式上與式（26）～式（28）相同，即

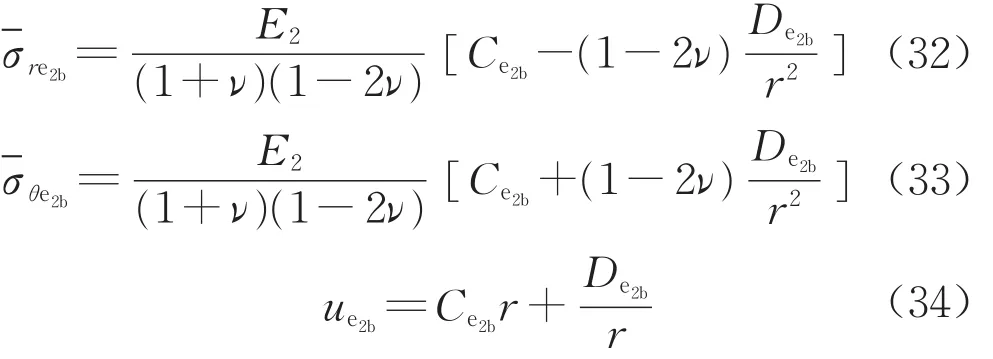
對于彈性問題，將已求解待定系數的表達式（26）和還未求解含有待定系數的表達式（29）、（32）代入式（23）得到徑向全應力σri，再將σri與增量位移表達式（31）、（34）代入彈性問題的定解條件（18）、（19）、（21）、（22），求解待定系數Ci，Di（i=e1，e2a，e2b），可得到彈性問題應力和位移的解析表達式。限于篇幅，文中未列參數具體表達式。

3.3 彈塑性階段應力/位移

平面應變條件下，塑性區的軸向應力σz為中間主應力［26］，而徑、環向應力的大小關系可通過井壁彈性解答中井口處的徑向應力和環向應力大小進行判斷。確定主應力順序后，聯立式（12）和式（16），并將滲流場表達式（9）代入，求解關于塑性區應力的微分方程，得到塑性區主應力的表達式。當環向應力為第一主應力時，微分方程為

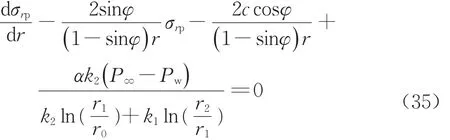
求得塑性區應力表達式為

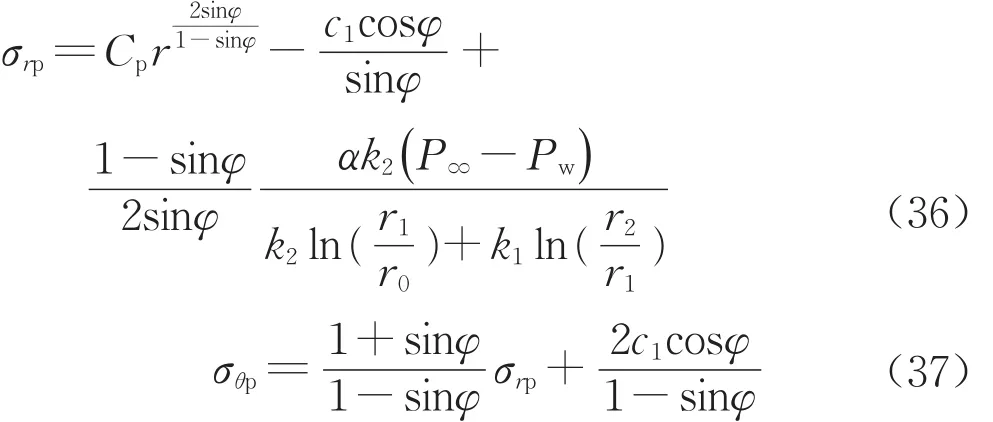
當徑向應力為第一主應力時，微分方程為

求得塑性區應力表達式為

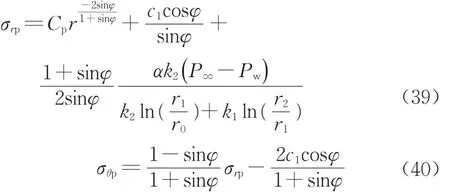
式中：Cp為待定系數，通過式（18）的邊界條件確定。可以看出塑性區應力與塑性區半徑沒有直接關聯。

下面求解增量位移。認為塑性區的總應變為塑性應變和彈性應變之和，可表示為

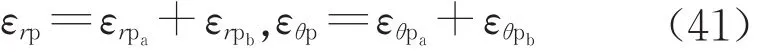
式中：εrpb和εθpb為塑性區的徑向和環向彈性應變。聯立式（17）和式（41）可得εrp+βεθp=εrpb+βεθpb，將式（13）代入該式左端后得到塑性區位移需滿足的微分方程如下：

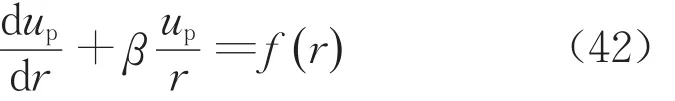
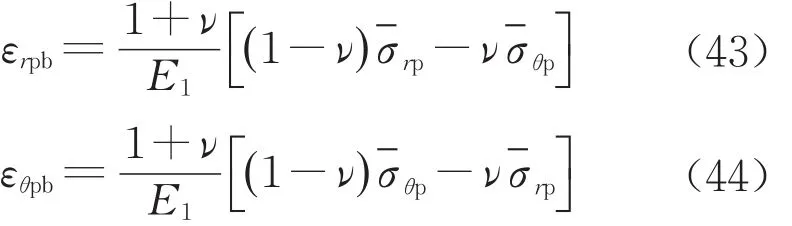
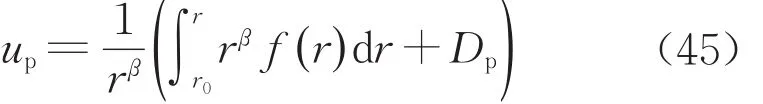
式中：Dp為待定系數。

在彈塑性階段，三個彈性區的應力和位移的控制方程與4.2節一致，將已求解待定系數的塑性區應力表達式（36）、（37）（或（39）、（40））和含待定系數的彈性區應力、位移表達式（29）～式（32）、（34），塑性區位移表達式（45）代入定解條件式（19）～式（22），得到關于待定系數Dp以及Ci、Di（i=e1，e2a，e2b）和塑性區半徑rp的方程組，待定系數可直接求解或寫成關于rp的表達式，最終可得到關于rp的超越方程，用數值方法求解rp后可確定各個待定系數的值，得到彈塑性問題的應力及位移解答。限于篇幅，此處未給出具體方程和結果。

3.4 模型驗證

為了驗證推導過程的正確性和模型的適用性，本節將數值模型的結果與本文解答進行比對。

利用ABAQUS軟件建立同等假設下的有限元模型進行比對驗證，如圖4所示。有限元模型選擇軸對稱的建模方式，分區從內到外依次為分解域、未分解域和無窮域。分解域大小需根據3.3節計算得到。首先給模型施加初始地應力和滲流壓力，并進行地應力平衡，第二步改變r=r0處的應力和滲場邊界條件，得到最終的應力和位移分布。參數設置如下：孔徑r0=0.2m，未分解域半徑r2=3m，彈性模量E1=40MPa，E2=100MPa，泊松比ν=0.3，黏聚力c1=0.5MPa，c2=2MPa，內摩擦角φ=23°，剪脹 角 ψ=0°，滲 透 系 數 k1/k2=4，熱 傳 導 系 數λ1/λ2=4，無窮遠處的應力、滲流壓力和溫度分別為σ∞=15.6MPa，P∞=12MPa，T∞=8°C，有效應力系數α=0.7。分解域半徑r1按第3節的推導過程計算，另取r3=150r0作為有限元模型的外邊界。在本文分析的參數范圍內，計算發現欠壓條件下環向應力為第一主應力，過壓條件下徑向應力為第一主應力。圖5a、圖5b分別給出欠壓模型（Pw=8MPa，Tw=18°C，r1=8.2r0）和過壓模型（Pw=21MPa，Tw=23°C，r1=4r0）的比對情況。在r=r1處由于分解域彈模劣化引起環向應力突變。結果表明解析解與有限元模型的應力、位移曲線及塑性區半徑均吻合較好。

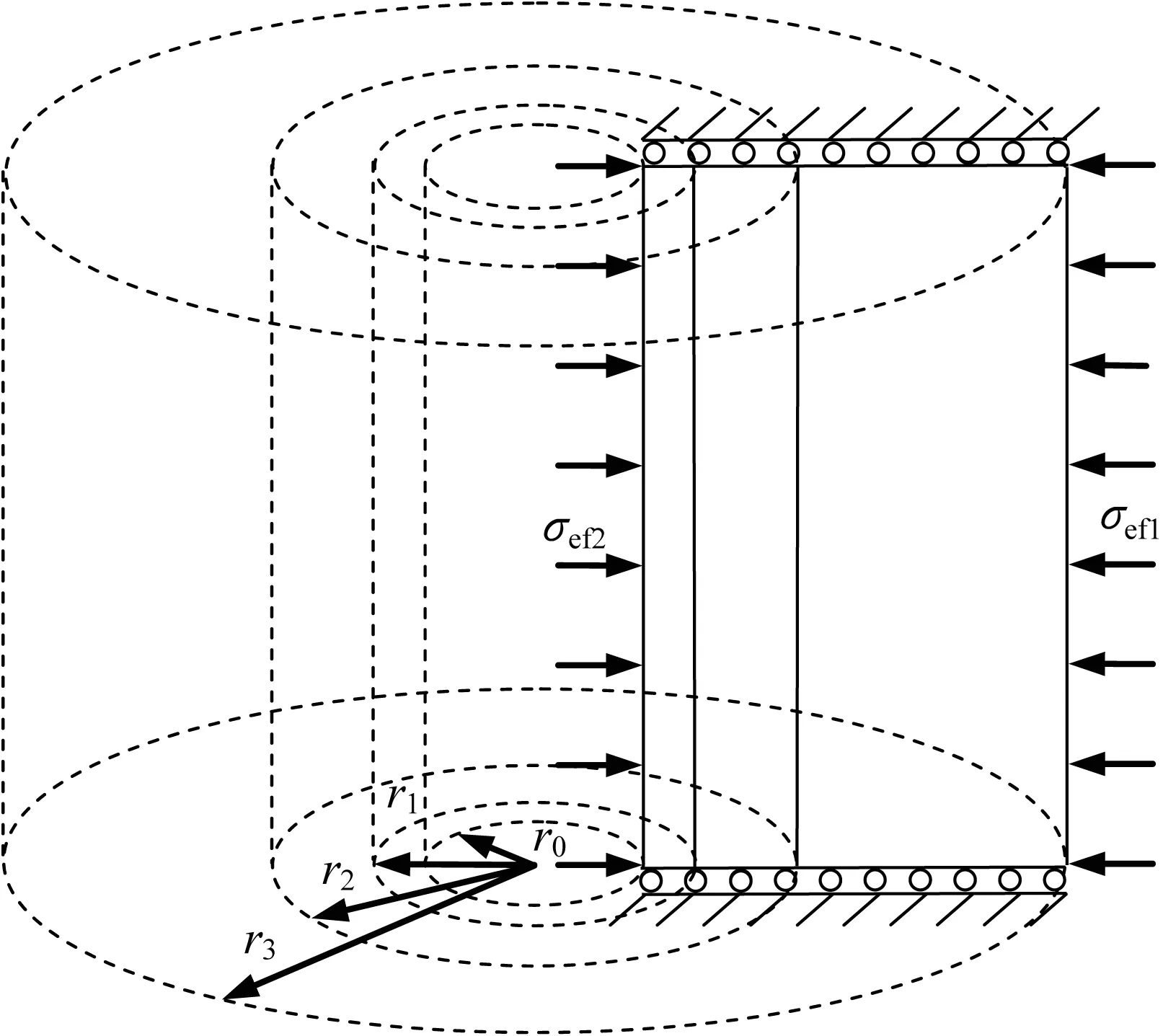
圖4 軸對稱有限元模型Fig.4 Axisymmetric model in finite element method

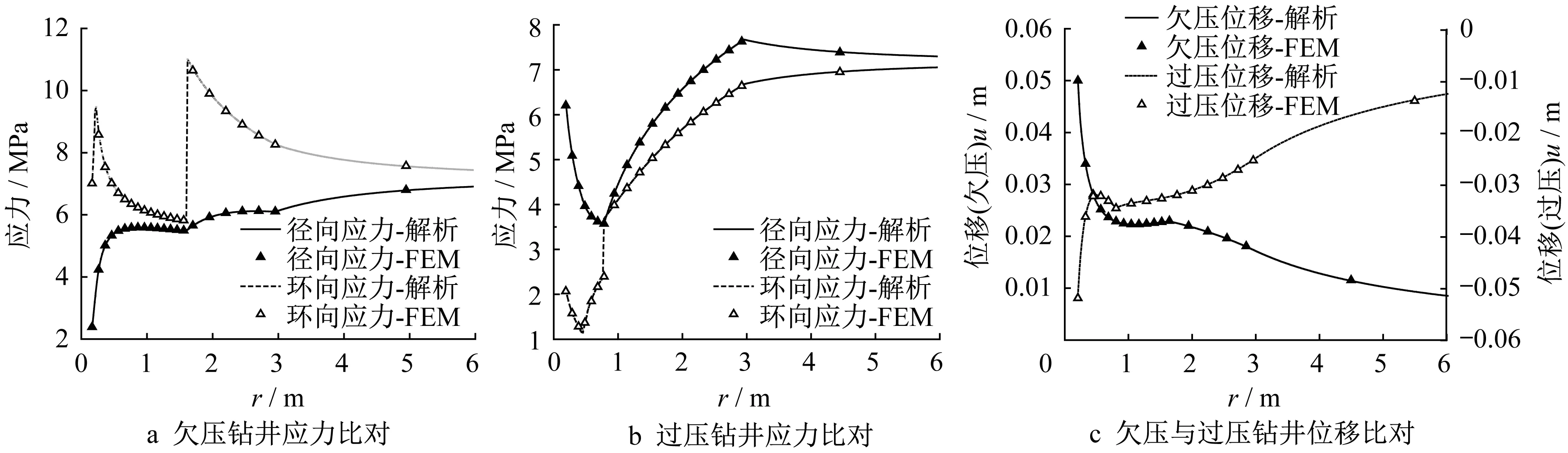
圖5 解析解與有限元結果比對Fig.5 Comparison between analytical solution and finite element results

由于目前缺乏含水合物地層井壁穩定的實驗和工程測量數據，本文通過與數值模型進行比對，驗證解析解答的適用性。圖6為本文應力解答與文獻［6］中基于復雜數值模型力場部分的結果比對。該數值模型基于南海神狐海域含水合物地區的測井數據，考慮了氣液兩相流，以及水合物分解和二次生成引起的熱量變化，求解了非穩態的滲流、溫度等物理場影響下的地層應力。選取t=24h的時刻，結果表明本文提出的解析解與數值解的徑向應力吻合較好，解析解的環向應力在近井壁處的塑性區內（A、B點）與數值解誤差較小，在距離井壁較遠的彈性區內（C點）略低于數值解，總體上應力沿徑向的變化趨勢與數值解一致，且塑性區半徑的結果相近。

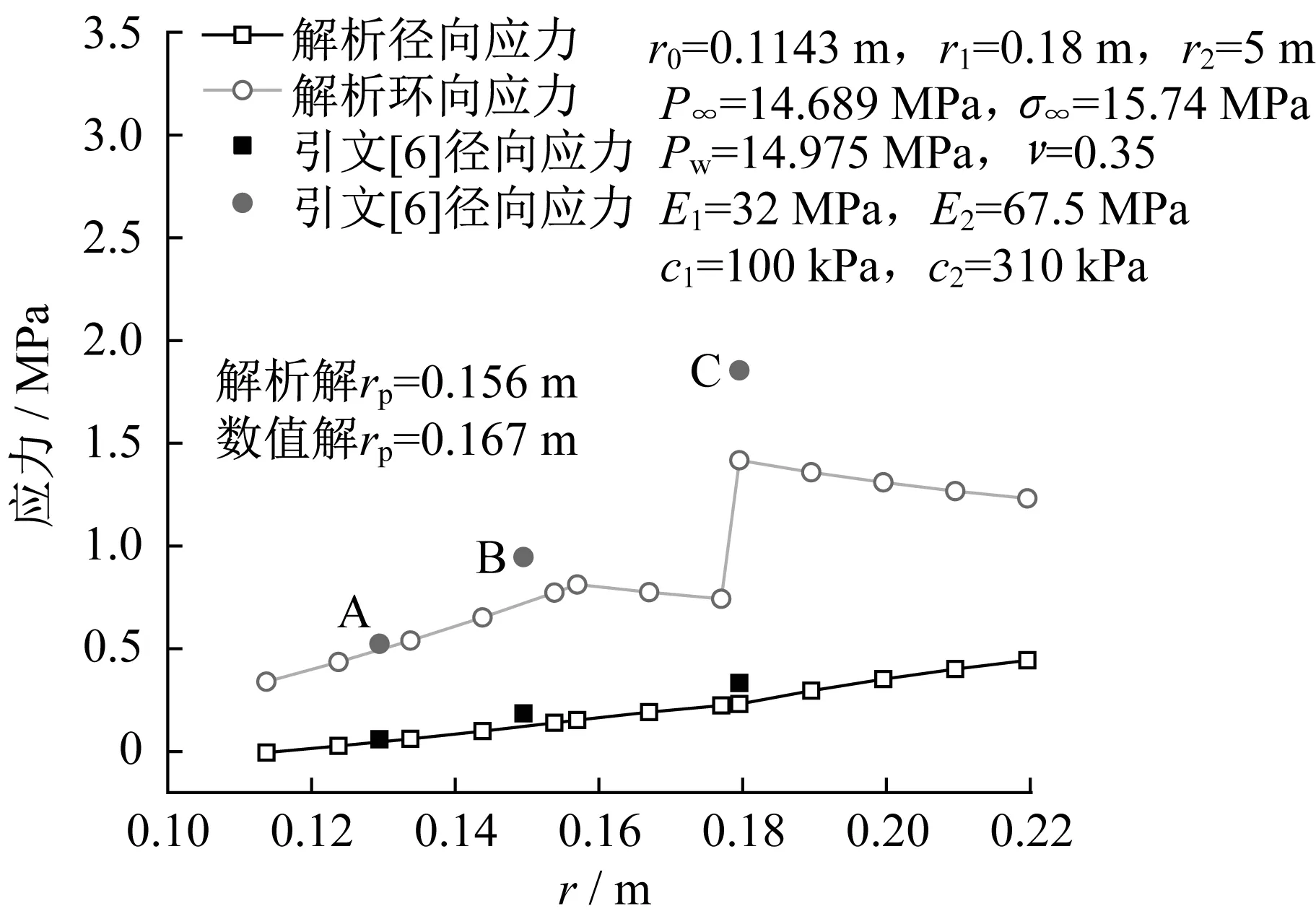
圖6 解析解與復雜模型數值結果比對Fig.6 Comparison between analytical solution and numerical solution under complex conditions

4 參數分析

儲層進入塑性或發生較大的位移會增大井壁失穩的風險，本文將用塑性區的大小和儲層的徑向位移反映井壁的穩定性。本節利用解析模型分析鉆井液壓力Pw、分解域大小r1、彈性模量劣化程度E1/E2以及黏聚力劣化程度c1/c2等因素對含水合物地層井壁穩定性的影響。取E2=100MPa，c2=2MPa，φ=18°，其它參數與4.4節相同。位移均采用量綱為一形式u/u0，其中u0=σ∞r0/2G2為無滲流、無鉆井液壓力、無水合物分解情況下井壁處位移，G2=E2/(1+2ν)為未分解域的剪切模量。

4.1 鉆井液壓力對力場的影響

鉆井液壓力對保持井壁穩定非常重要，過大或過小均會引起井壁失穩。為僅凸顯鉆井液壓力的影響，通過調節溫度Tw使分解域半徑均為r1=4r0。圖7～圖8分別給出欠壓和過壓鉆井情況不同鉆井液壓力下位移和應力隨位置的變化。不同情況的Pw和Tw已在圖中給出。可以看出鉆井液壓力對徑向應力影響較小，對環向應力的影響較為明顯。由位移變化可知，欠壓鉆井時，井眼附近塑性變形較為嚴重，隨著與井壁距離的增大位移逐漸減小；當鉆井液壓力增大時，井壁的徑向位移和塑性區半徑逐漸減小。過壓鉆井時，由于井壁附近孔隙壓力較高，水合物不易分解，井壁不易進入塑性。只有當鉆井液溫度和壓力值非常高時才會出現明顯的分解域和塑性區。由圖8b可知，過壓條件下最大徑向位移不一定出現在井壁邊緣（r=r0），當鉆井液壓力較小時可能出現在未分解域（r1＜r≤r2）中，且塑性區位移相比于欠壓鉆井時更小；塑性區位移對鉆壓的變化較為敏感，隨著鉆井液壓力增大，井壁的徑向位移和塑性區半徑逐漸增大。

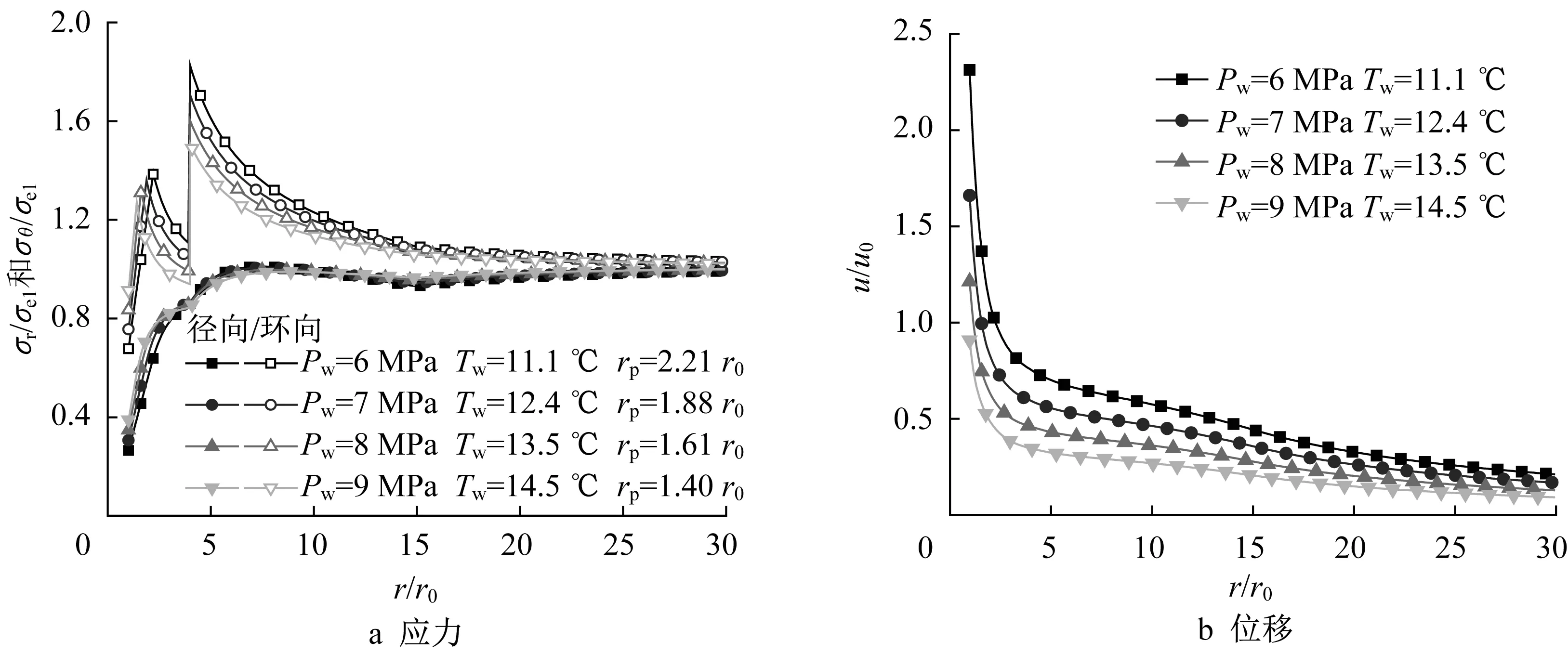
圖7 欠壓鉆井時鉆井液壓力對應力和位移的影響Fig.7 Influence of drilling fluid pressure on stress and displacement under underbalanced drilling condition

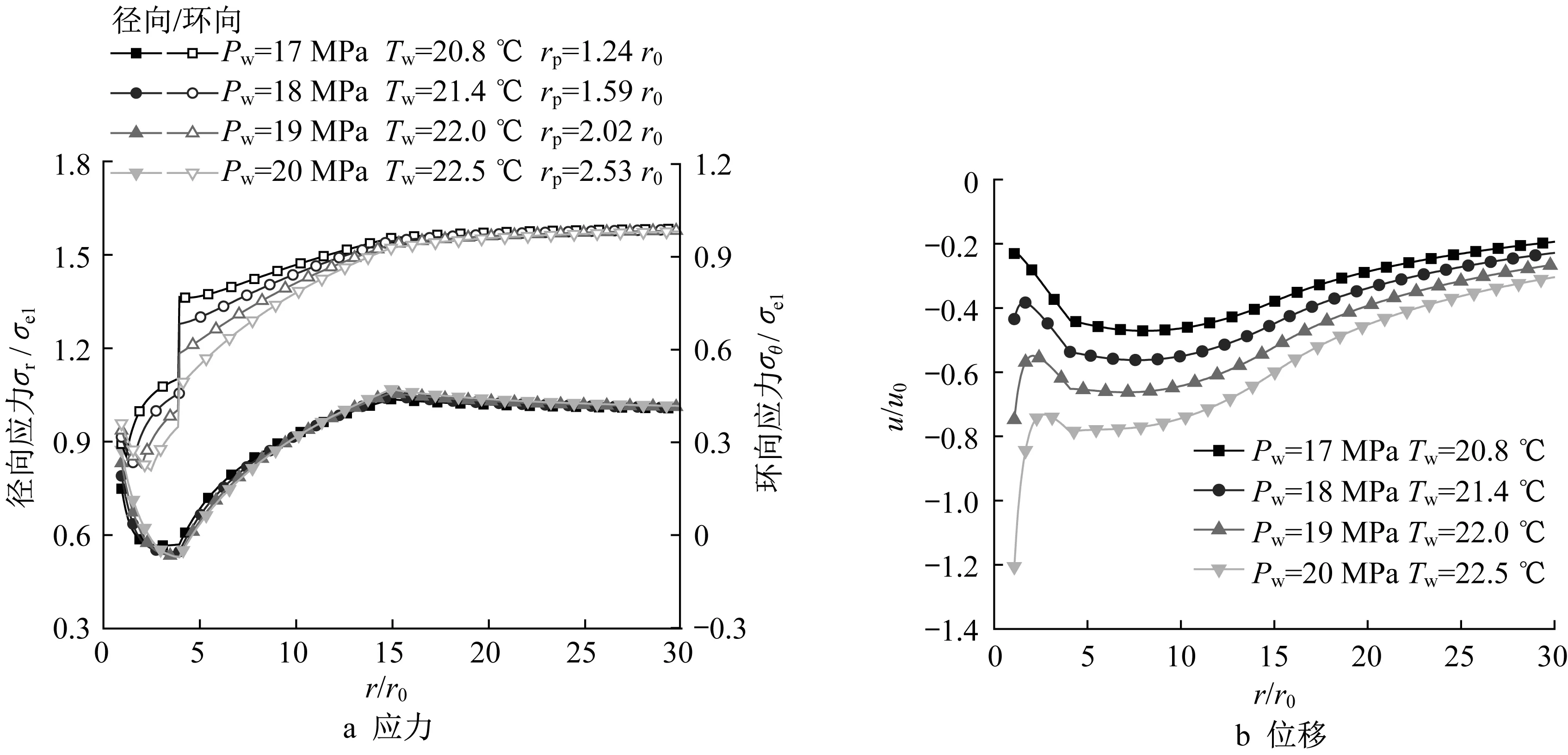
圖8 過壓鉆井時鉆井液壓力對應力和位移的影響Fig.8 Influence of drilling fluid pressure on stress and displacement under overbalanced drilling condition

4.2 分解域半徑對塑性區范圍的影響

當分解域變大時，塑性區變大的程度是水合物地層鉆井時關注的重要問題。保持鉆井液壓力不變，通過調節Tw改變分解域范圍，圖9給出欠壓和過壓鉆井下塑性半徑（rp）隨分解域半徑的變化，其中分解域的黏聚力和彈性模量分別為c1=0.25c2，E1=0.5E2。當r1/r0=1時表示水合物未分解，由圖可見，隨著分解域范圍的擴大，塑性區先是急劇增大，然后增大趨勢逐漸變緩，且始終沒有超出分解域，與本文的假設一致。對比兩組數據可以發現，隨著分解域的擴大，過壓鉆井模型的塑性區比欠壓鉆井模型增長更快。

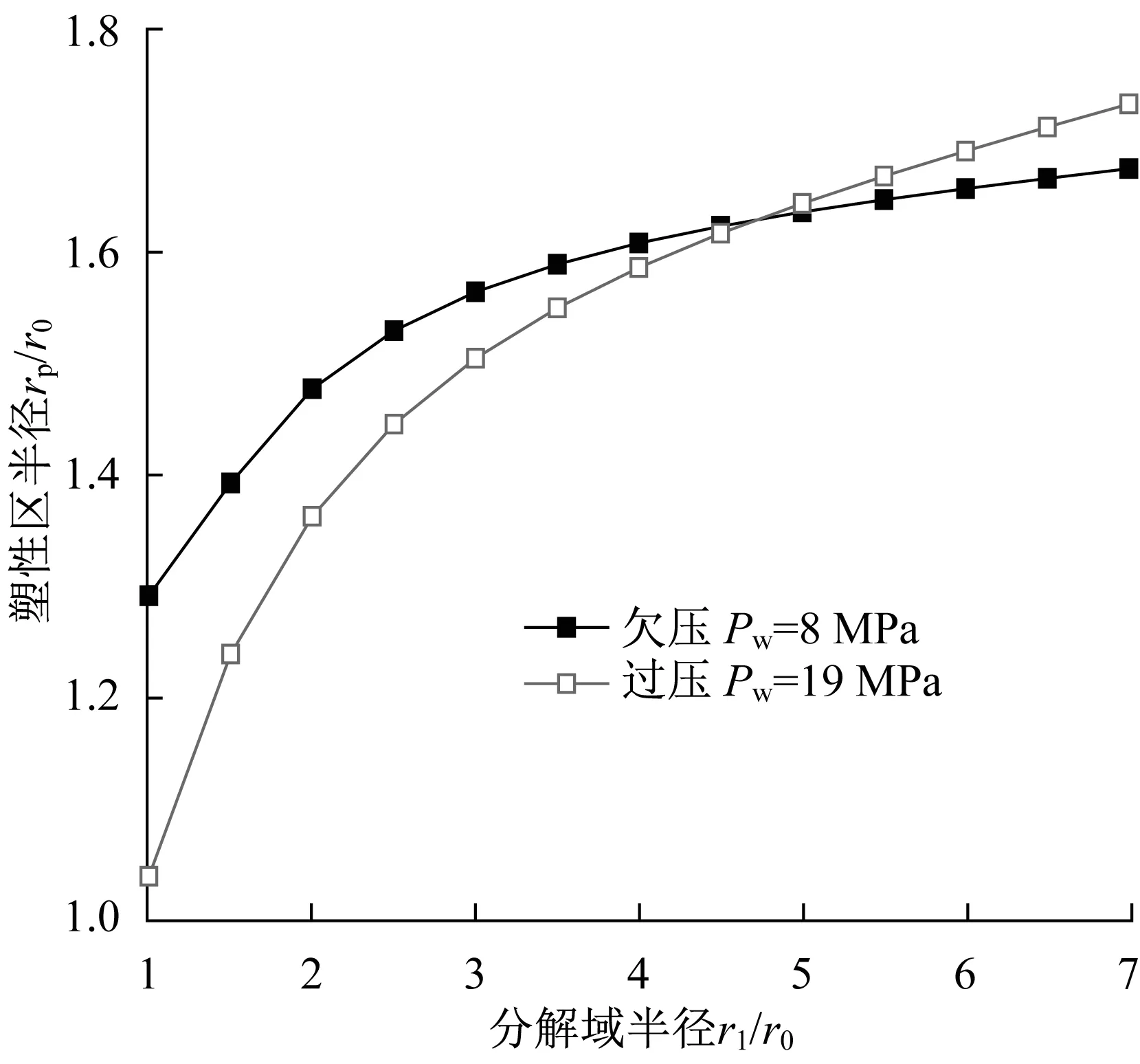
圖9 分解域大小對塑性區半徑的影響Fig.9 Influence of the size of dissociation region on the radius of plastic zone

4.3 彈性模量/黏聚力劣化程度對力場的影響

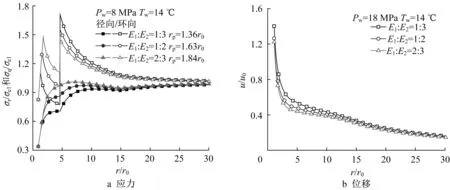
圖10 欠壓鉆井時彈性模量劣化程度對應力和位移的影響Fig.10 Influence of the reduction of elastic modulus on stress and displacement under underbalanced drilling condition

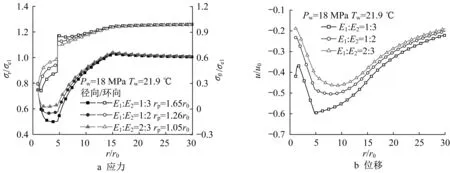
圖11 過壓鉆井時彈性模量劣化程度對應力和位移的影響Fig.11 Influence of the reduction of elastic modulus on stress and displacement under overbalanced drilling condition

考慮到實際情況由于水合物分解所引起的彈模劣化程度有限，僅在一定范圍內對參數進行討論。保持分解域半徑一致（r1=4.7r0），取c1=0.25c2，圖10～圖11給出欠壓和過壓鉆井時不同彈模劣化程度下的應力和位移分布。可見彈模變化對塑性區應力值無影響，但對塑性區大小有影響。欠壓鉆井時，隨著彈性模量劣化程度的提高，塑性區逐漸減小；過壓鉆井時，隨著劣化程度的提高塑性區逐漸增大。兩種情況下，隨著彈模劣化程度提高，徑向應力在全域內逐漸減小，而環向應力在分解域內逐漸減小，在未分解域內逐漸增大。位移方面，隨著彈模劣化程度的提高，地層的徑向位移有小幅增長，對欠壓情況的影響更為明顯。黏聚力劣化程度對塑性區的影響如圖12所示，保持分解域半徑一致（r1=4.7r0），取E1=0.5E2。可以看出，欠壓和過壓鉆井下分解域內黏聚力劣化越嚴重，塑性區半徑rp越大，且呈現近似線性的關系。水合物有多種賦存類型，其中膠結型水合物的分解對儲層的黏聚力影響最大，因此分解引起的塑性區增長相比于其它類型的水合物儲層將更為顯著。

圖12 黏聚力劣化程度對塑性區大小的影響Fig.12 Influence of the reduction of cohesive on plastic radius

5 結論

本文采用Mohr-Coulomb屈服準則和理想彈塑性模型模擬水合物地層，給出鉆井過程井壁穩定模型力學響應解析解答，與同假定和復雜模型的有限元結果吻合很好，可以進行含水合物地層中井壁穩定的分析。利用解析模型進行的參數分析顯示：

（1）鉆井液壓力對環向應力和徑向位移的影響較為明顯。過壓鉆井情況下，當鉆井液壓力較低時徑向位移的峰值可能出現在彈性區。

（2）水合物分解使塑性區范圍顯著增大，隨著分解域范圍的擴大，塑性區的增長呈現先快后慢的趨勢，且過壓情況下塑性區的增長更快，當分解域半徑達到3r0～4r0后塑性區的增長速度較小并趨于穩定。

（3）彈模劣化程度的提高在欠壓情況下將引起塑性區減小，在過壓情況下將引起塑性區增大。而黏聚力的劣化則必然導致塑性區增大，且劣化程度與塑性區半徑之間近似線性關系。

本文在建立解析模型時選取的強度準則與本構關系較為簡單，后續工作將考慮鉆井過程的化學因素及分解域完全變塑的情況，并結合水合物儲層的力學特性，建立更加符合實際情況的解析模型，為工程問題提供建議。