城市軌道交通正線列車故障發生概率預測模型

王鎮波，葉霞飛，沈 堅，施董燕

（1.同濟大學道路與交通工程教育部重點實驗室，上海201804；2.同濟大學上海市軌道交通結構耐久與系統安全重點實驗室，上海201804；3.上海申通地鐵集團有限公司技術中心，上海201103）

城市軌道交通列車故障是造成正線運營延誤甚至中斷的主要原因之一［1-2］，不僅影響乘客正常出行，還埋下許多安全隱患。為此，《地鐵設計規范》［3］規定正線上每隔5～6座車站或8～10 km設置停車線，以確保列車在正線任何位置發生故障后，將其處理下線的救援時間控制在30 min以內。但是整個城市軌道交通生命周期內因停車線起作用而降低故障列車對正線運營影響程度所帶來的效益是否高于額外修建停車線所產生的土建及維護成本一直是個值得關注的問題。其中，列車故障發生概率的高低對正線運營的影響程度差異很大，應是設置停車線時除了救援時間之外需要考慮的一個重要參數。因此，深化列車故障發生概率的合理預測方法意義重大，可為停車線設置方法的進一步完善提供列車故障發生概率參數取值的依據。

在理論上，一起列車故障就是一次貝努利試驗的結果，每一列車在開行某個班次時，它如果順利完成即成功，如果發生列車故障即失敗。而城市軌道交通列車每日發生故障一般屬于小概率事件，這使得出現一次失敗所需的貝努利試驗次數十分巨大。針對這一特點，很多學者往往采用離散型分布中的泊松分布［4］或負二項分布［5-6］構建模型，其中泊松分布要求均值等于方差，負二項分布則適用于方差明顯大于均值的情況。隨著研究與應用的進一步深入，出現了有零過多現象的數據，如每列車短時期內發生故障的次數，這種數據中0的個數要明顯多于由泊松分布與負二項分布隨機產生的個數，因而采用零膨脹泊松分布［7-8］、零膨脹負二項分布［9］的研究逐漸興起。

考慮到在停車場等非正線上發生的列車故障不影響列車正常運營，本文選擇城市軌道交通列車在正線上發生故障的概率作為重點研究對象（以下提及的列車故障發生概率若無特別說明，均指城市軌道交通列車在正線上發生故障的概率）。首先定性分析列車故障發生概率的主要影響因素，之后基于實際數據生成包含這些影響因素的離散型數據集，在此基礎上從泊松分布、負二項分布、零膨脹泊松分布、零膨脹負二項分布中選擇合適的分布及可能的函數形式構建備選模型并標定，最后通過模型比選確定最終的城市軌道交通正線列車故障發生概率預測模型。

1 列車故障發生概率主要影響因素

從產品構成的角度來看，城市軌道交通列車由多節車廂串聯而成，任一車廂的部件出現損壞時，均視作該列車的一起故障，而編組越多的列車擁有的部件會越多，出現故障的可能性也就越高。因此城市軌道交通列車的編組數應對其故障發生概率產生顯著影響，且列車故障發生概率會因列車編組數增加而變高。

從產品使用的角度來看，城市軌道交通列車具有系統集成度高、設備種類多、設備工況復雜等特點，剛投入使用的列車需要經歷一段部件磨合期才能達到最佳使用狀態［10］，所以整列車的故障發生概率在使用初期往往會比較高。在部件磨合期結束后，整列車的故障發生概率應處于相對較低的階段，之后隨著列車走行公里的累計，部件老化及磨損的問題則可能會使整列車的故障發生概率有所回升。由此可見，城市軌道交通列車自投入運營開始的累計走行公里應對其故障發生概率產生顯著影響，且列車故障發生概率會因累計走行公里增加而呈現先高后低再高的特點。

需要注意的是，城市軌道交通列車在整個壽命周期中會經歷各種類型的維修，目前計劃修是國內外城市采用的主流列車維修方式［11-13］，即只要設備到了規定時期就需進行維修與替換。在國內計劃修的維護規程中，架修和大修均需要對車輛解體并更換一系列設備重新組裝，架修涉及車輛的大部分部件，而大修則是全面性深層修理［10］。經過架修或大修后的列車幾乎接近新車，所有因累計走行公里產生的部件損耗及老化將全部消除，應對其故障發生概率產生顯著影響。

考慮到城市軌道交通列車每日發生故障一般屬于小概率事件，需要在一定的走行公里范圍內對其進行觀察。根據《地鐵設計規范》［3］，新建地鐵工程的車輛架修和大修周期分別應為60萬km、120萬km，在無法得到詳細行車資料的情況下可分別采用5年、10年的時間間隔，則走行公里與時間間隔之間的關系可依此推算為12萬km對應1年。為此，本文在生成離散型數據集時選擇以12萬km為間隔劃分每列車的累計走行公里，觀測其在每個12萬km內發生故障的次數。在這個觀測范圍下，可以減小季節氣候、列車擁擠度［8，14］等因素對列車故障發生概率預測精度的影響程度。

綜上所述，最終通過定性分析得到的列車故障發生概率的主要影響因素為列車編組數、累計走行公里、架修或大修經歷。下面將基于實際數據生成包含上述影響因素的離散型數據集。

2 數據來源及處理

2.1 數據來源

本文數據由某城市軌道交通公司提供，具體包括全網各線列車的首次正式投入使用日期、2011至2019年間架修和大修記錄、2017至2019年間故障記錄（含故障發生的時間、地點及原因）、編組情況以及全網各線2011至2019每年總列車運營里程。

經過初步數據整理，共有910列對象列車、600起在正線上發生的列車故障記錄。首先，剔除了其中投入運營時間不明（35列）、列車編組有變更（2列）、架修和大修記錄缺失（76列）的對象列車。其次，考慮到因偶然因素造成的列車故障隨機性太強，為了避免各類偶然因素對主要影響因素的干擾，剔除了因異物卡阻（30起）、乘客沖門（15起）、其余偶然因素（56起）造成的列車故障記錄。最終保留了797列對象列車、499起列車故障記錄作為后續研究的基礎數據。

2.2 數據處理

基礎數據未直接給出列車的累計走行公里，需要通過列車的累計運營時間乘以日均走行公里進行推算。

列車的累計運營時間可根據列車的首次正式投入使用日期、架修和大修記錄確定。首先用列車首次正式投入使用日期作為累計運營時間的起始日期，之后查詢列車是否有過架修或大修經歷，如果有，則累計運營時間的起始日期需更換為列車完成最近一次架修或大修后正式投入使用的日期，以重置其累計運營時間。至于是否應對架修后的列車和大修后的列車進行區分，考慮到架修和大修的本質都是對列車部件進行更新，只是大修更全面徹底，所以如果造成列車故障的部件均在架修和大修時涉及檢修和更換，則無需對兩者進行區分。為此，對列車故障成因進行統計，如圖1所示。基于文獻［15］并結合圖1可知，除“其他”以外的列車故障成因所涉及的部件均會在架修和大修中進行檢修和更換，故本文不再對兩者進行區分。

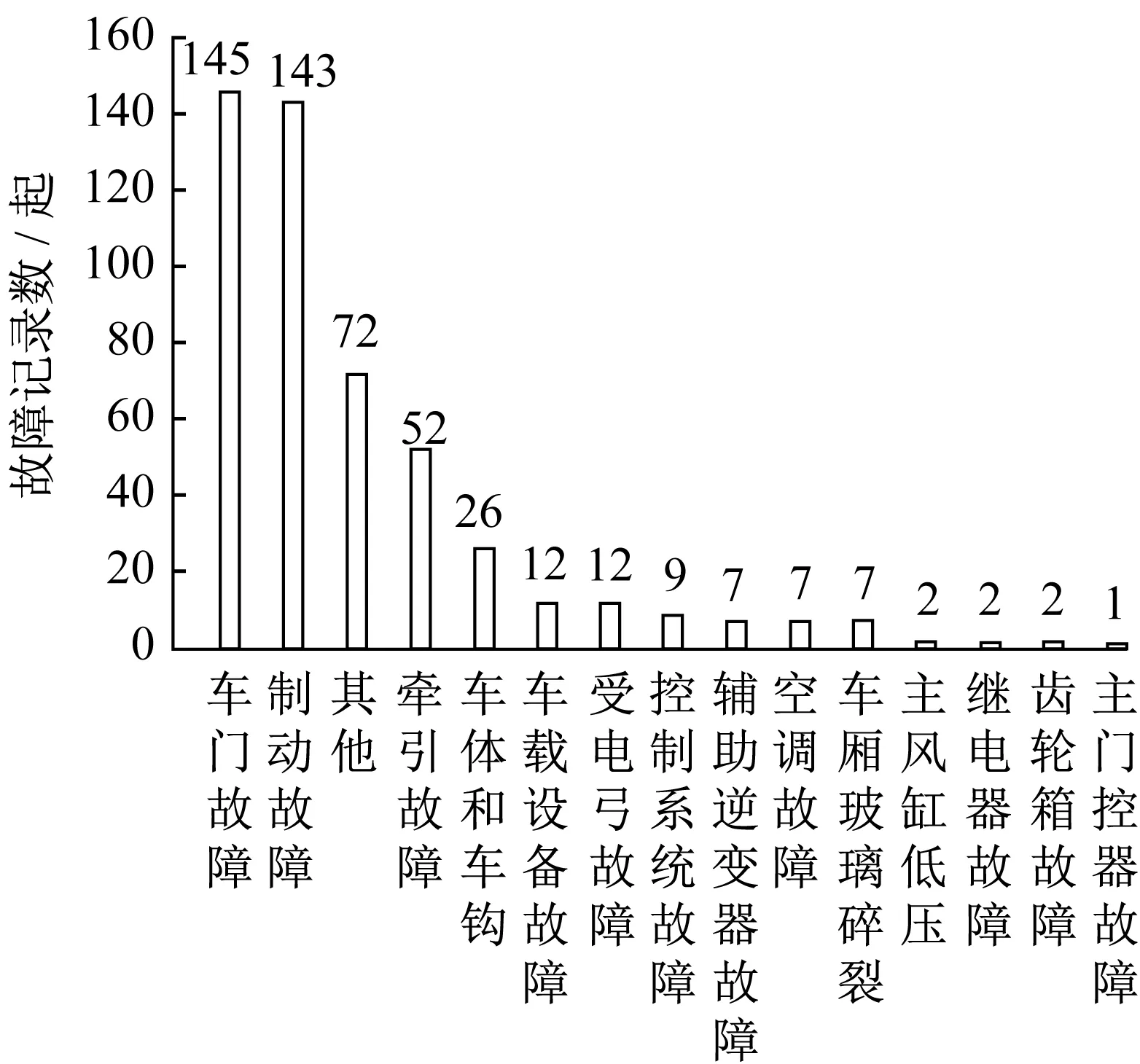
圖1 列車故障成因統計Fig.1 Statistics of train fault cause

日均走行公里通常由年總列車運營里程除以年總列車數再除以365d得到，但其忽略了該年新上線列車實際開行天數不到365d的問題，從而導致日均走行公里偏小。本文在計算日均走行公里時對此做了改進，即

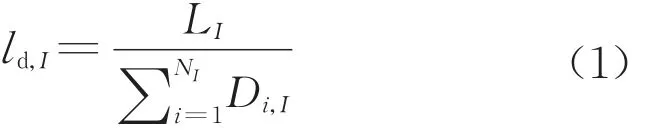
式中：ld，I為列車在第I年日均走行公里，km·d-1；LI為第I年總列車運營里程，km；NI為第I年總列車擁有數，列；Di，I為第i列列車在第I年實際開行天數。

在實現列車累計走行公里的可推算后，以12萬km為間隔將其依次劃分出多個累計走行公里階段并確定每個階段的起止日期。由于列車故障記錄的時間范圍為2017至2019年，因此只能將起止日期均在2017至2019年內的累計走行公里階段作為統計對象，對列車在該階段發生故障的次數進行計數，具體步驟如圖2所示。

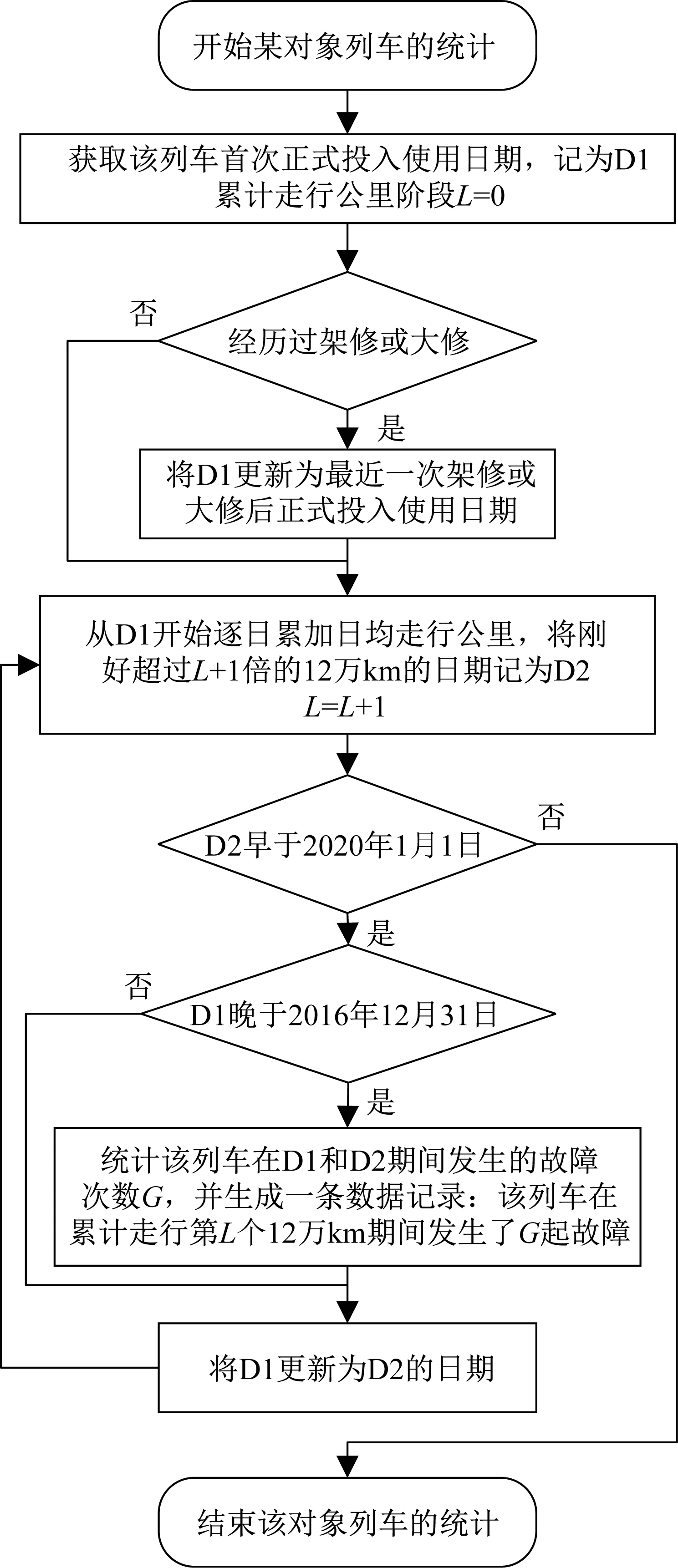
圖2 單列車在各累計走行公里階段故障發生次數的數據生成Fig.2 Data generation of fault occurrence number for single train in each cumulative running kilometer period

在基礎數據的797列對象列車中，有130列因正式投入運營時間較晚未在2017至2019年完成第1個12萬km階段，未被計入數據集。在剩余的對象列車中，分別有271、325、71列在2017至2019年完成了1、2、3個12萬km階段，在數據集中相應地被計入1、2、3次。在基礎數據的499起列車故障記錄中，有254起的發生日期未在其關聯的對象列車于2017至2019年完成任一12萬km階段的起止日期范圍內，未被計入數據集。因此，最終生成的數據集中共有1134列對象列車（重復的對象列車因所處累計走行公里階段不同而具有獨立性，故視作一列新的對象列車），245起列車故障記錄。各累計走行公里階段的統計情況如表1所示。

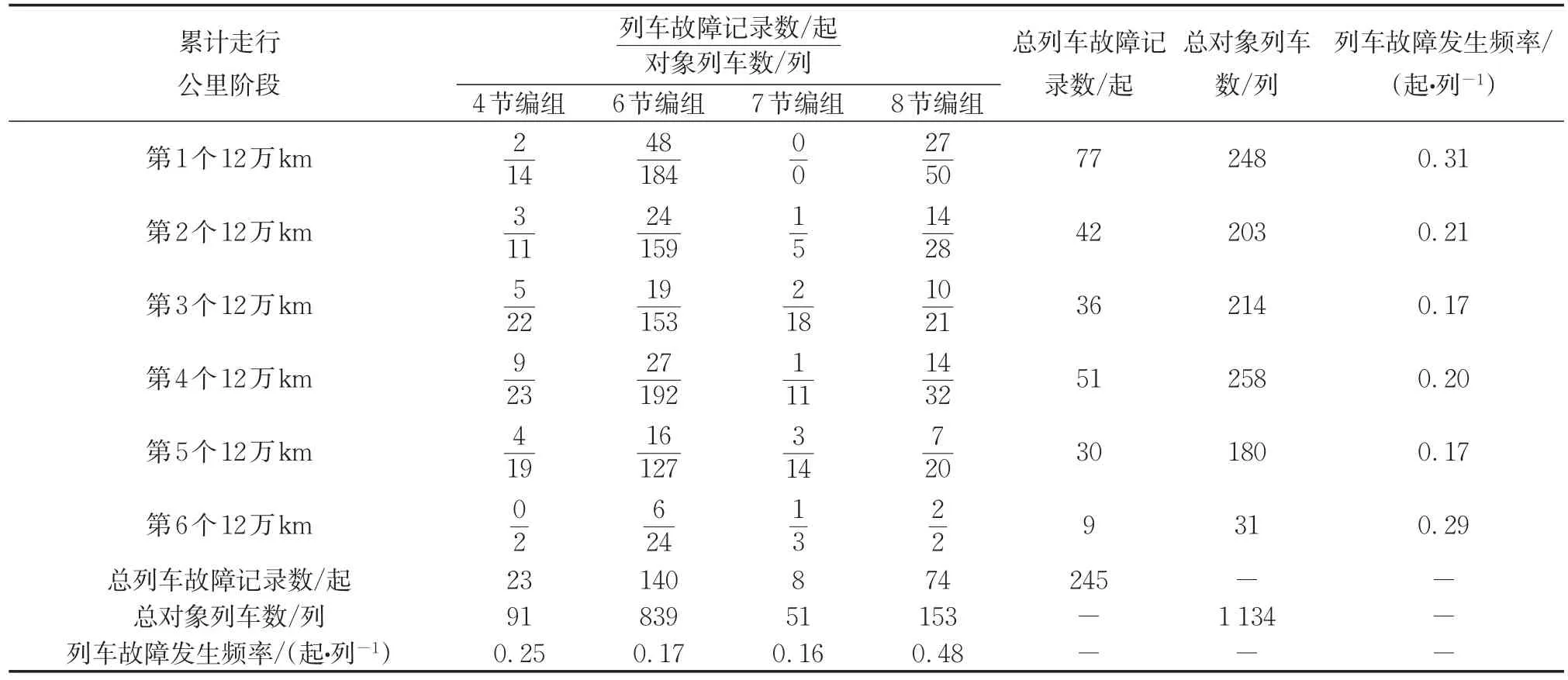
表1 各累計走行公里階段統計情況Tab.1 Statistics of each cumulative running kilometer period

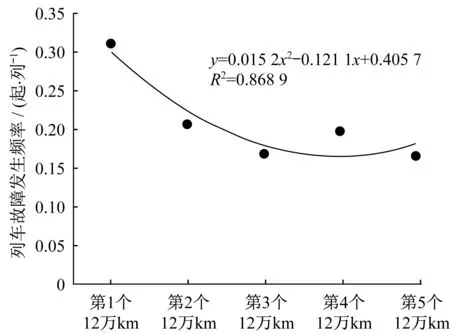
圖3 列車故障發生頻率隨累計走行公里階段變化的趨勢Fig.3 Trend of train fault frequency with cumulative running kilometer period

從表1可知，隨著累計走行公里階段的推移，列車故障發生頻率基本符合先減少再回升的規律，二次拋物線形式較適合描述該影響規律，如圖3所示。8節編組的列車故障發生頻率最高，但整體來看不同列車編組數的列車故障發生頻率之間沒有明顯的遞變規律，這可能是由于4、7節編組的總對象列車數較少導致其頻率有一定的異常和不穩定性，從而干擾了變化規律的直觀判斷。為此采用專門描述定序分類變量間相關程度的Kendall相關系數［16］分析列車編組數與列車故障發生次數之間的影響規律，結果兩者的Kendall相關系數為0.13，p值為5.65×10-6小于0.05，由此可認為列車編組數與列車故障發生次數正相關，一定程度上印證了之前關于列車編組數對列車故障發生概率影響的定性分析。

3 列車故障發生概率預測模型

3.1 備選模型

為了從泊松分布、負二項分布、零膨脹泊松分布、零膨脹負二項分布中選擇合適的分布構建模型，需觀測離散型數據集內不同列車故障發生次數的出現頻數，并計算列車故障發生次數總體均值及方差，結果如圖4所示。從中可知，列車故障發生次數總體均值與方差十分接近，這符合泊松分布的要求，而列車故障發生0次的數據占比達到81.2%，不能忽視可能存在的零過多現象，故零膨脹泊松分布也值得嘗試。因此，選擇泊松分布與零膨脹泊松分布構建相應的備選模型。

泊松分布在離散數據分析中相當常用。假定隨機變量Y服從泊松分布，則其概率函數如下：

式中：λ為泊松參數，一旦確定即可計算隨機變量Y取不同值的概率；y為列車走行一個12萬km期間在正線上發生故障的次數。

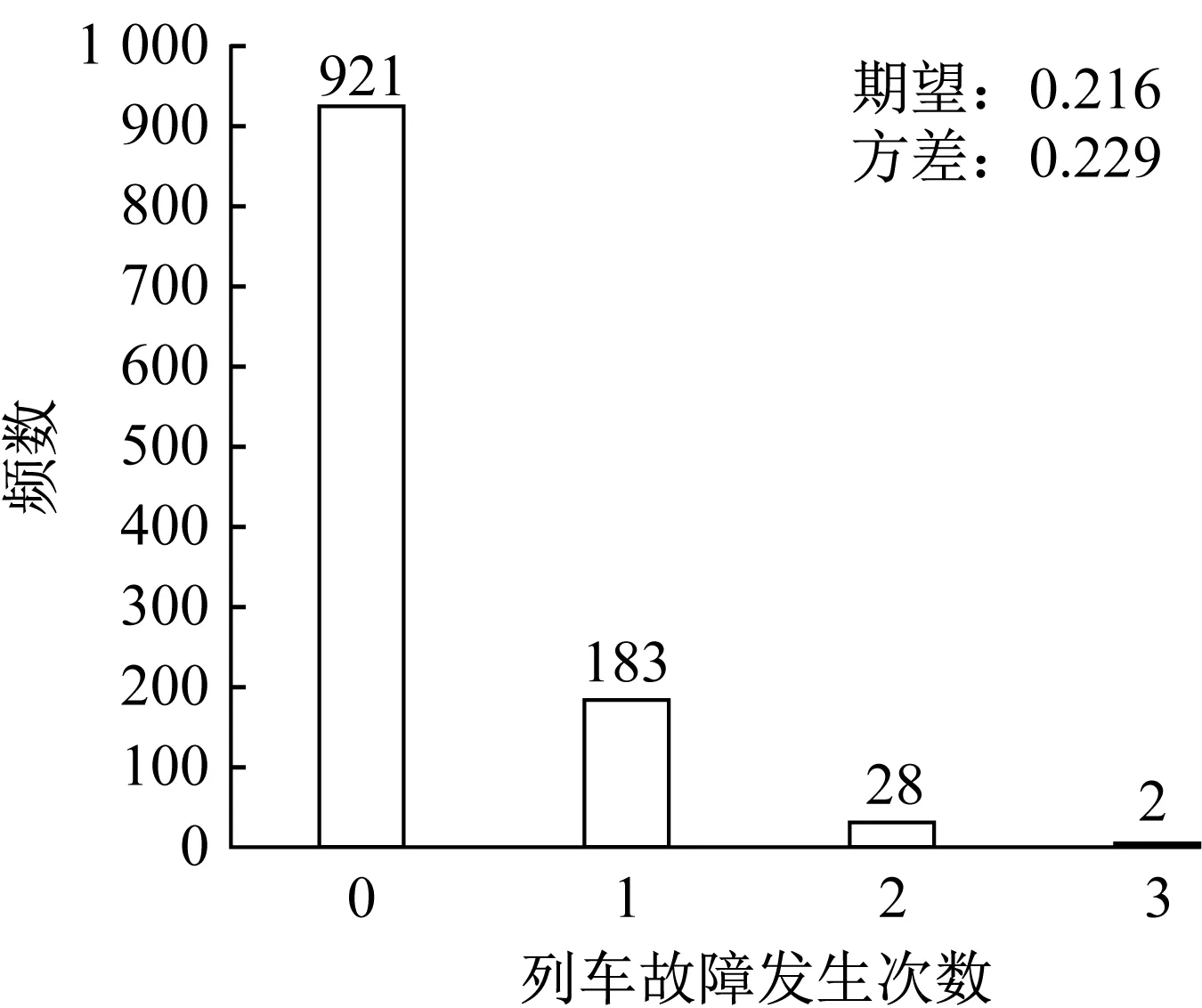
圖4 列車故障發生次數的觀測頻數Fig.4 Observation frequencies for different train fault occurrence numbers

只要建立泊松參數與列車編組數、列車當前所處累計走行公里階段的序號之間的回歸方程，即可實現考慮各主要影響因素情況下列車故障發生概率的預測。泊松參數與自變量之間的回歸通常采用對數線性模型［17］，且累計走行公里階段推移對列車故障發生概率的影響規律較適合用二次拋物線描述，由此得到模型一如下：

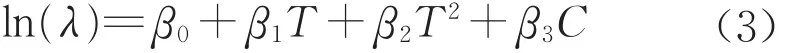
式中：T為列車當前所處累計走行公里階段的序號，取值為1，2，…，對應第1，2，…個12萬km階段，在架修或大修后需重新累計；C為列車編組數，根據國內常 用 的 編組 形式 ，取 值 一 般 為 4，5，6，7，8；β0，β1，β2，β3為待估系數。

零膨脹泊松分布是在泊松分布的基礎上考慮數據集存在零過多現象而提出的分布。假定隨機變量Y服從零膨脹泊松分布，則其概率函數如下：

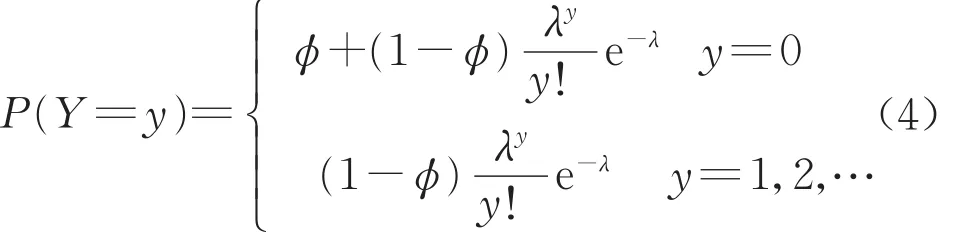
式中：φ為零膨脹參數，表示取值為0的非泊松數據所占的比例。當0＜φ＜1時，數據集存在零過多現象，若φ=0，則式（4）將退化為式（2）。當泊松參數與零膨脹參數都確定后，才可計算隨機變量Y取不同值的概率。

泊松參數與零膨脹參數應彼此獨立并均與主要影響因素有所關聯，為此需對泊松參數、零膨脹泊松參數與列車編組數、列車當前所處累計走行公里階段的序號進行兩兩組合來建立回歸方程，共有2種可能的組合方案。泊松參數與自變量之間的回歸依舊采用對數線性模型，零膨脹參數與自變量之間的回歸通常采用logistic回歸模型［17］，且累計走行公里階段推移對列車故障發生概率的影響規律仍用二次拋物線描述，由此得到模型二、模型三，分別如下：

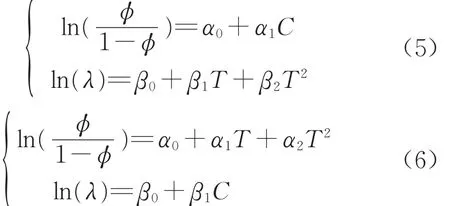
式中：α0，α1，α2為待估系數。

3.2 系數標定

三個備選模型中待估系數的標定基于極大似然估計，通過Gauss-Newton迭代法獲得數值解［17］，顯著性水平取0.05，具體計算過程由Stata數據分析軟件完成。

各備選模型的估計結果如表2所示，各模型中變量C的系數均反映了列車編組數的增加會提高列車故障發生概率，變量T和T2的系數均反映了累計走行公里的增加會使列車故障發生概率先降低后回升。其中，模型一中所有變量均通過顯著性檢驗，模型成立；模型二中泊松參數與零膨脹參數的常數項未通過顯著性檢驗，在經過各種可能的嘗試后，發現剔除泊松參數的常數項可使剩余變量均通過顯著性檢驗，由此得到改進后的模型二；模型三中零膨脹參數的變量均未通過顯著性檢驗，在經過各種可能的嘗試后，發現模型三始終無法成立，故在后續模型比選時不再考慮。

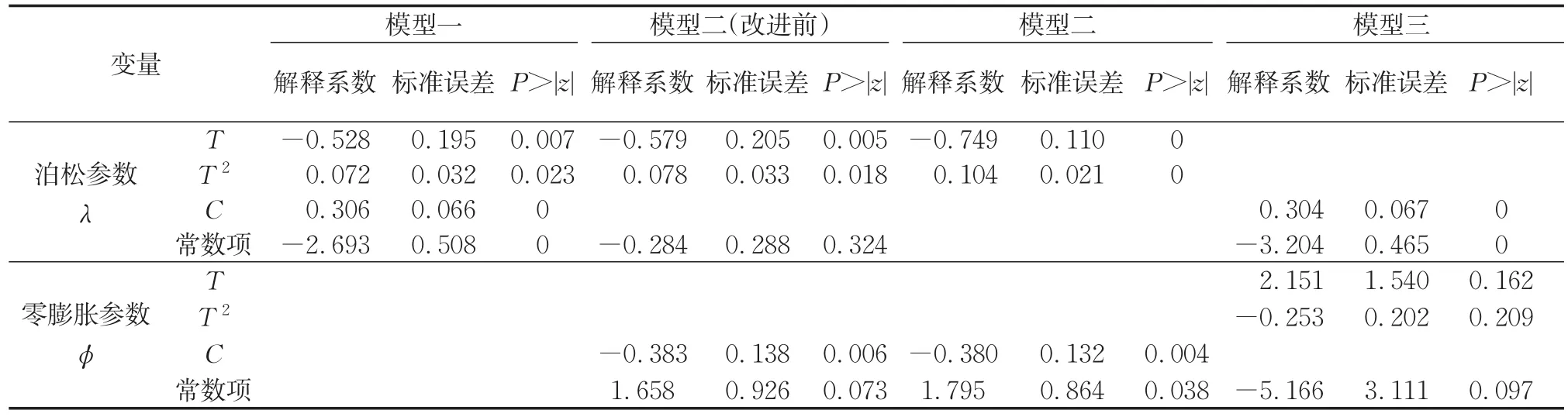
表2 模型估計結果Tab.2 Estimated results of alternative models

3.3 模型比選

針對模型一和模型二，從兩方面定量比較兩者的優劣。首先，比較兩個模型所預測的不同累計走行公里階段總列車故障記錄數與實際值的平均差異程度δ，計算方法見式（7）。該數值越低說明模型預測效果越好，具體結果見表3。

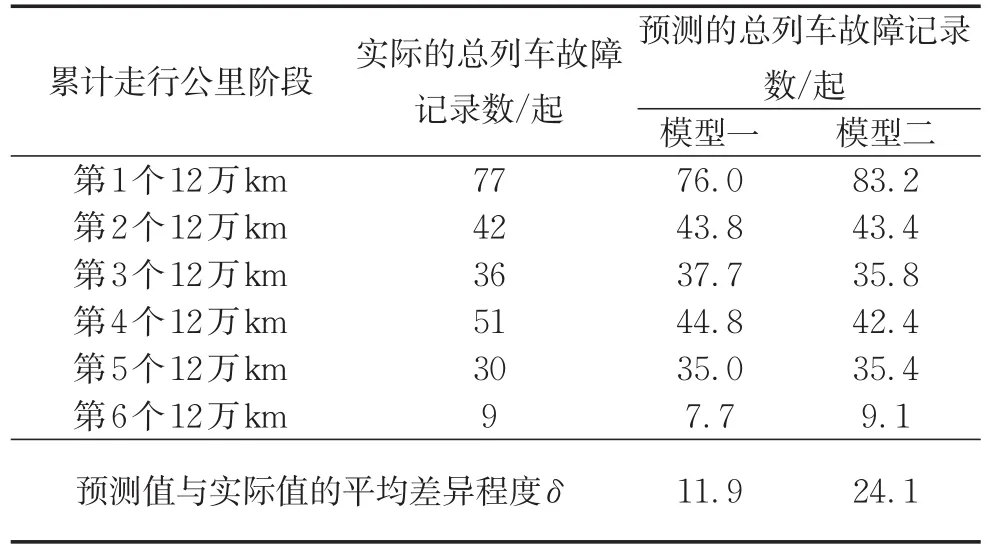
表3 各累計走行公里階段總列車故障記錄數的預測結果Tab.3 Predicted results of total train fault records in each cumulative running kilometer period

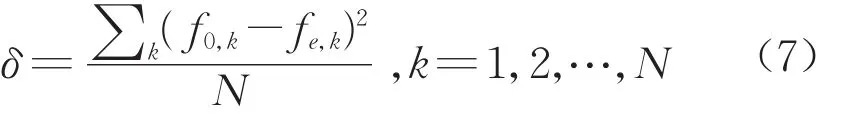
式中：f0，k為第k個階段實際的總列車故障記錄數；fe，k為第k個階段預測的總列車故障記錄數；N為階段個數。

其次，繪制ROC曲線比較兩個模型的泛化能力，ROC曲線下包含的面積越大，模型泛化性能越好［8］。需要注意的是，ROC曲線的適用范圍是二分類問題，而兩個模型中列車故障發生次數存在0、1、2、3起的類別，屬于多分類問題，所以需要進行二分類的轉化：列車未發生故障（0起）、列車發生了故障（1起以上）。繪制得到的ROC曲線如圖5所示。

從比較結果來看，模型一無論是預測效果還是泛化能力均優于模型二。因此，最終的城市軌道交通正線列車故障發生概率預測模型如下：

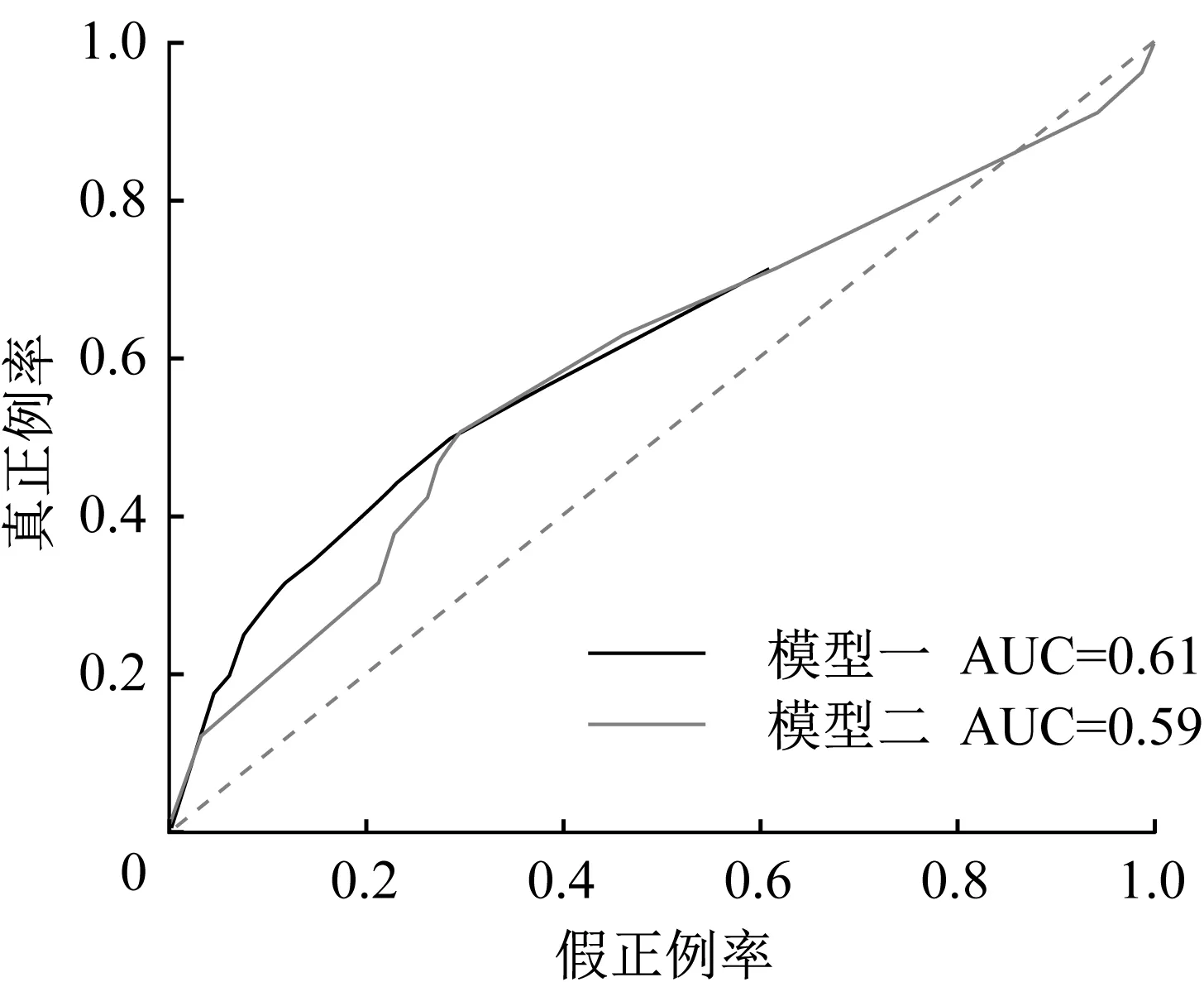
圖5 各備選模型的ROC曲線Fig.5 ROC curves for each alternative model

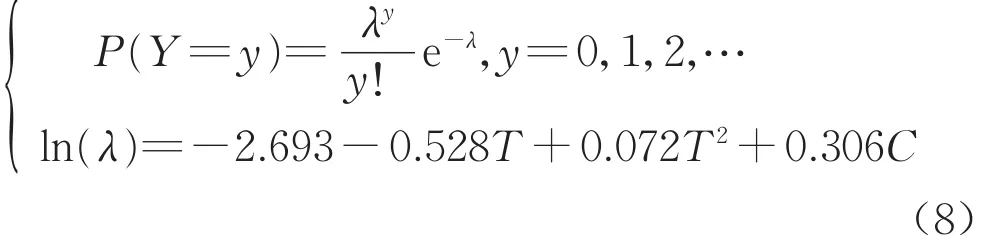
確定泊松參數后，便可通過1-P(Y=0)得到列車故障發生概率。不同列車編組數、累計走行公里階段組合下的列車故障發生概率如表4所示。通過比較列車故障發生概率在橫向、縱向的增長情況可知，在城市軌道交通列車處于第6個12萬km階段之前，相比于累計走行公里階段的推移，列車編組數的增加對列車故障發生概率的影響更大。這可能是因為整列車可視為由多節車廂組成的串聯系統，車廂數越多整列車的可靠性越低，而每節車廂的可靠性只有在達到一定使用程度后才會發生大的變化，從而導致了很長一段時間內整列車的故障發生概率更容易受列車編組數的影響。

表4 不同影響因素組合下的列車故障發生概率Tab.4 Train fault probabilities corresponding to different combinations of influencing factors

4 結論

以城市軌道交通列車為研究主體，綜合考慮多方因素，提出了基于泊松分布的城市軌道交通正線列車故障發生概率預測模型。主要研究工作總結如下：

（1）通過定性分析得到列車編組數、累計走行公里、架修或大修經歷為列車故障發生概率的主要影響因素。當列車經歷架修或大修后，需重新累計其走行公里。

（2）探究了各影響因素對列車故障發生概率的影響規律：列車編組數的增加會提高列車故障發生概率；累計走行公里的增加會使列車故障發生概率先降低后回升。

（3）以每12萬km為觀測范圍生成單列車在一定走行公里內故障發生次數的離散數據集，基于數據呈現的分布特征選擇泊松分布、零膨脹泊松分布構建了3個備選模型。之后根據顯著性檢驗、預測值與實際值的平均差異程度以及ROC曲線進行模型比選，結果顯示基于泊松分布的模型最優。由此提出了基于泊松分布的城市軌道交通正線列車故障發生概率預測模型。

（4）根據模型結果可推斷：在列車編組數固定的情況下，列車故障發生概率會在列車投入運營后的第4個12萬km階段達到最低值，在第7個12萬km階段超過初始值。