計算覆蓋粗糙集最大和最小描述的矩陣新方法

劉財輝,謝德華,溫燕軍,凌敏

(贛南師范大學 數學與計算機科學學院,江西 贛州 341000)

0 引言

經典粗糙集理論是由波蘭著名學者Pawlak[1]于20世紀80年代初提出來的,是一種處理不精確和不確定性的分析理論。由于它能高效地處理不確定性數據,目前已被廣泛運用于機器學習、模式識別和數據挖掘等領域。近年來,隨著數據量的劇增和數據分析的廣泛應用,關于粗糙集理論的研究也越來越受到重視[2]。隨著研究的深入,人們發現建立在等價關系基礎上的經典粗糙集理論在某些情況下并不適用,因此,覆蓋粗糙集的概念應運而生。它將經典粗糙集中的等價劃分拓展為一般的覆蓋,是粗糙集理論的一種重要擴展,不僅拓寬了粗糙集理論的應用領域,也增強了處理復雜數據的能力[3-4]。

在覆蓋粗糙集理論中,許多基本問題的研究都涉及最大、最小描述,因而如何計算最大和最小描述成為研究的熱點之一。對于數據量較小的數據集而言,計算其最大、最小描述,可以采用集合的方法,但對于體量較大的數據集,直接用集合的方法計算會有計算量大、效率低下等問題。因此,人們試圖借助在計算機上易操作的可分辨矩陣方法來解決此類問題[5-8]。陳文[9]等分析了基于覆蓋的上近似定義方法,并提出最小上近似的概念。陳文等[10]從對偶性、正域可定義性、負域可定義性及邊界可定義性等幾個方面對覆蓋上、下近似算子進行了分類,為提出矩陣方法提供了理論基礎;王磊等[11]利用論域子集的布爾列矩陣、等價關系矩陣及其誘導矩陣三者的數量積運算,提出了一種基于矩陣的粗糙集上、下近似的計算方法;汪小燕[12]等提出了多粒度粗糙集二進制矩陣,并通過實例證明了用矩陣表示上、下近似的有效性。程燕等[13]則利用覆蓋粗糙集的特征布爾矩陣、鄰域矩陣以及新定義的三種矩陣運算,探索了覆蓋粗糙集的上、下近求解問題;林姿瓊等[14]給出了覆蓋的矩陣、特征矩陣、重量矩陣,通過定義的新運算“?”以及最小、最大描述的計算函數求解最大、最小描述;最近,Wang等[15]以及Liu等[16]對覆蓋粗糙集的最大和最小描述的矩陣方法進行了深入和系統的研究。本文受文獻[15]和[16]的啟發,提出了一種改進的計算覆蓋粗糙集的最大和最小描述的矩陣方法,該方法能夠減少運算量,降低運行時間復雜度。

本文在第1節中,給出了覆蓋粗糙集和最大、最小描述的相關定義;第2節主要回顧了Wang等和Liu等提出的基于覆蓋的粗糙集中極小描述和極大描述問題的矩陣方法,并在此基礎上提出了一種改進方法;在第3節中,為了驗證本文所提方法的正確性和有效性,我們在6個UCI數據集上進行了實驗分析比較,結果表明我們的方法在保證正確性的前提下,計算時間要優于已有方法；第4節進行了總結和展望。

1 基本概念

最大、最小描述是覆蓋粗糙集中兩個重要的概念,為了后述方便,本節定義了覆蓋粗糙集最大、最小描述。

定義1 (覆蓋[17]) 設U為論域,C為U的一個子集簇,如果C中所有的集合均不為空且有∪C=U,那么稱C為U上的一個覆蓋。

定義2 (最小描述[4,18]) 給定覆蓋近似空間U是論域C是U的一個覆蓋對任意的x∈U稱mdC(x)={K∈C|x∈K∧(?S∈C∧x∈S∧x∈S∧S?K?K=S)}為x的最小描述。

定義3 (最大描述[4,18]) 給定覆蓋近似空間U是論域,C是U的一個覆蓋,對任意的x∈U稱MDC(x)={K∈C:x∈K∧(?S∈C)(x∈S∧K?S?K=S)}為x的最大描述。

2 計算覆蓋粗糙集最大和最小描述的矩陣方法及其改進

首先介紹了文獻[15]和文獻[16]所提的計算方法,并分析其時間復雜度,在此基礎上提出一種改進方法。通過分析新方法的時間復雜度,可以發現,與文獻[15]和文獻[16]的方法相比較,新的方法計算量大大降低,時間復雜度大大下降。新方法為計算最大和最小描述,特別是在較大數據集的情形下計算最大和最小描述,提供了新思路和新技術。

2.1 計算覆蓋粗糙集最大和最小描述的Wang方法

定義4[10]設U={x1,…,xm}為論域,C={K1,K2,…,Kn}為U上的一個覆蓋,則矩陣A(C)=(aij)m·n稱為覆蓋C的一個矩陣表示,其中

下面用一個例子來說明如何獲得覆蓋的矩陣表示。

例1 論域U={x1,x2,x3,x4,x5},覆蓋集C={K1,K2,K3,K4},其中K1={x1,x2},K2={x1,x3},K3={x1,x2,x3}K4={x2,x4,x5},根據定義4,C可用矩陣表示如下:

x1x2x3x4x5

定義5[11]設C={K1,…,Kn}為論域U={x1,…,xm}的一個覆蓋,則

(1)當bij=|Ki∩Kj|,我們有A(C)·AT(C)=(bij)n×n;

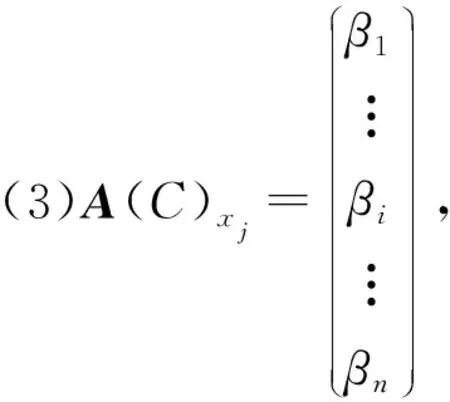
例2 (接例1)

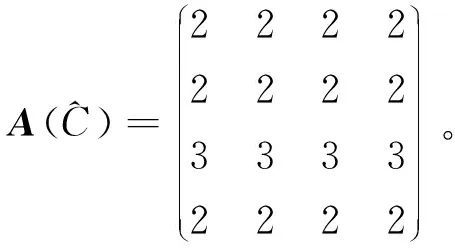
定義6[15]設C={K1,…,Kn}為U={x1,…,xm}的一個覆蓋,A(C)xj·AT(C)xj=(ast)n×n,則有ast=|Ks∩Kt|,且ast>0當且僅當xj∈Ks∩Kt,其中“·”表示矩陣的乘法, “AT”表示矩陣A的轉置。

定義7[15]設A1=(aij)m·n以及A2=(bij)m·n為兩個矩陣,定義操作“?”為A3=A1?A2=(di)n×1,而此時

定義8[15]設C={K1,…,Kn}為U={x1,…,xm}的一個覆蓋,對于任意C1?C可定義

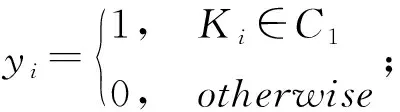
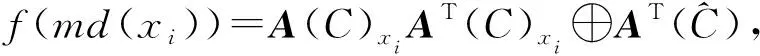
因此md(x1)={K1,K2}。

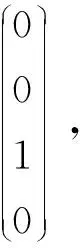
同理可以求出關于x2,x3,x4,x5的最大、最小描述。我們將文獻[15]的計算方法歸納為算法1,經過分析可以得到算法1的總時間復雜度為O(|C||U|+(|C|+|C|2)|U|),其中第12-30步為該算法的主要步驟,其時間復雜度為O((|C|+|C|2)|U|)。

2.2 計算覆蓋粗糙集最大和最小描述的Liu方法

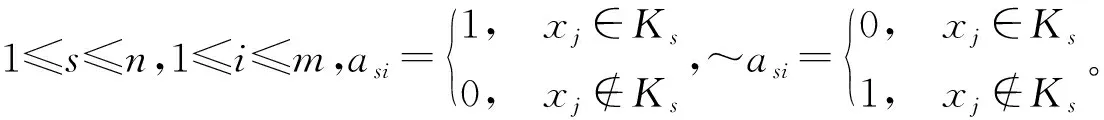
定理1[16]令C={K1,K2,…,Kn}為全集U={x1,…,xm}上的一簇覆蓋,A(C)=(aij)m×n是C的矩陣表示對于任一Ks,Kt∈C(s≠t),A(Ks)·AT(～Kt)=0當且僅當Ks?Kt.

定義10[16]令C={K1,K2,…,Kn}為U={x1,…,xm}上的一簇覆蓋,Ks∈C。

定義

定理2[16]令C={K1,K2,…,Kn}為全集U={x1,…,xm}上的一簇覆蓋,Ks∈C,特征函數ψ(md(xj))=(φt)n×1。若φt=1則Kt∈md(xj)否則Kt?md(xj)。

算法1 計算最大和最小描述的Wang方法輸入:論域U={x1,…,xm}U上的一個覆蓋C={K1,…,Kn}A(C)=(aij)mn輸出:md(xj),MD(xj)Begin1:m←|U|2:n←|C|∥輸入論域U和覆蓋C3: for i=1→n do4: for j=1→m do5: if xj∈Ki then aij=16: else aij=07: end if8: computeA(C)A(^C)∥計算C的矩陣描述9: end for10: end for11: compute AT(^C)12: for j=1→m do13: for i=1→n do14: computeA(C)xj15: computeAT(C)xj∥計算覆蓋C中xj的矩陣描述及其轉置矩陣16: end for17: computeA(C)xj·AT(C)xj18: for i=1→n do19: for k=1→n do20: if((A(C)xj·AT(C)xj(i,i)=AT(^C)(i,i))∧(i≠k?(A(C)xj·AT(C)xj(i,k)≠AT(^C)(i,k)))21: thenf(md(xj)(i))←1,md(xj)←Ki∥計算得到xj的最小描述22: else f(md(xj)(i))←023:end if24:if((A(C)xj·AT(C)xj(i,i)=A(^C)(i,i))∧(i≠k?(A(C)xj·AT(C)xj(i,k)≠A(^C)(i,k)))25: then f(MD(xj)(i))←1,MD(xj)←Ki∥計算得到xj的最大描述26: else f(MD(xj)(i))←027: end if28: end for29:end for30:end for31:return md(xj),MD(xj)

定義11[16]令C={K1,K2,…,Kn}為全集U={x1,…,xm}上的一簇覆蓋,Ks∈C, 定義

定理3[16]令C={K1,K2,…,Kn}為全集U={x1,…,xm}上的一簇覆蓋,Ks∈C,特征函數ζ(MD(xj))=(ηs)n×1。若ηs=1,則Kt∈MD(xj),否則Kt?MD(xj)。

例4(接例1)結合上述定義,可知

A(K1)·AT(～K2)=

(1,1,0,0,0)·(0,1,0,1,1)T=1

A(K1)·AT(～K3)=

(1,1,0,0,0)·(0,0,0,1,1)T=0

A(K1)·AT(～K4)=

(1,1,0,0,0)·(1,0,1,0,0)T=1

A(K2)·AT(～K1)=

(1,0,1,0,0)·(0,0,1,1,1)T=1

A(K2)·AT(～K3)=

(1,0,1,0,0)·(0,0,0,1,1)T=0

A(K2)·AT(～K4)=

(1,0,1,0,0)·(1,0,1,0,0)T=2

A(K3)·AT(～K1)=

(1,0,1,0,0)·(1,0,1,0,0)T=2

A(K3)·AT(～K2)=

(1,1,1,0,0)·(0,1,0,1,1)T=1

A(K3)·AT(～K4)=

(1,1,1,0,0)·(1,0,1,0,0)T=2

A(K4)·AT(～K1)=

(0,1,0,1,1)·(0,0,1,1,1)T=2

A(K4)·AT(～K2)=

(0,1,0,1,1)·(0,1,0,1,1)T=3

A(K4)·AT(～K3)=

(0,1,0,1,1)·(0,0,0,1,1)T=2。

綜上,由定理1可得:K1?K3,K2?K3

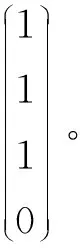
根據定義10和定義11,結合K1?K3,K2?K3,即可得到如下結論:

同理,

上面討論的方法可以概括為算法2,算法2的總時間復雜度為O(|C||U|+|C|+|C|2|U|)。 步驟10-20是算法2的主要部分,用于計算最小和最大描述,其時間復雜度為O(|C|+|C|2|U|)。

2.3 改進后的計算最大和最小描述的LXW方法

經過分析,我們發現要求元素xi的最大、最小描述只需在A(C)xi的基礎上進行分析計算即可,下面詳細介紹該方法。

定義12 設C={K1,…,Kn}為U={x1,…,xm}的一個覆蓋,我們定義

算法2 計算最大和最小描述的Liu方法輸入:論域U={x1,…,xm}U上的一個覆蓋C={K1,…,Kn}A(C)=(aij)mn輸出:md(xj),MD(xj)Begin1 m← |U|, n ← |C|;2 for i=1 → n do3 for j=1 → m do4 if xi∈K then5 aij=1;6 else7 aij=0;8 for i=1 → n do9 computeA(Ki) andAT(～Ki)∥計算得到Ki的矩陣描述10 for i=1 → n do11 for j=1 → m do12 for k=1 → n do13 if i≠k∧A(Ki)·AT(～Ki)=0 then14 ψ(md(xj)(k))←0;ζ(MD(xj)(i))←0;15 else16 ψ(md(xj)(k))←1;ζ(MD(xj)(i))←1;17 if ψ(md(xj)(k))≠0 then18 md(xj)←Ki∥計算得到最小描述19 if ζ(MD(xj)(i))≠0 then20 MD(xj)←Ki∥計算得到最大描述21 Return md(xj);MD(xj)

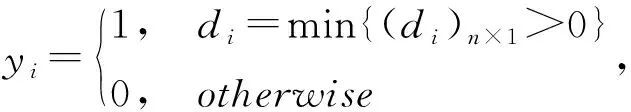
“min”表示取最小值,“min{(di)n×1>0}”表示先選擇出(di)n×1>0的一部分數值,然后計算其最小值。“max”表示最大值,“max{(di)n×1>0}”表示先選擇出(di)n×1>0的一部分數值,然后計算其最大值。當得到的為最小值時,將最小值賦值為1,其余的賦值為0,當得到的為最大值時,將最大值賦值為1,其余的賦值為0。

定理4 設C={K1,…,Kn}是U={x1,…,xm}上的一個覆蓋,給定特征函數g(md(xj))=(yi)n×1,如果yi=1,則有Ki∈md(xj),否則Ki?md(xj)。

若令dr,dt為其中兩個描述,假設dr為最小描述。則

dr=min(dr,dt)?dt-dr>0?

(dt1-dr1)+(dt2-dr2)+…(dtn-drn)>0?

(|Kt∩K1|-|Kr∩K1|)+

(|Kt∩K2|-|Kr∩K2|)+…

(|Kt∩Kn|-|Kr∩Kn|)>0

反之,若

(|Kt∩K1|-|Kr∩K1|)+

(|Kt∩K2|-|Kr∩K2|)+…

(|Kt∩Kn|-|Kr∩Kn|)>0

成立,則dt-dr>0成立,因此定理4成立。

定理5設C={K1,…,Kn}是U={x1,…,xm}上的一個覆蓋,給定特征函數h(MD(xj))=(zi)n×1,如果hi=1,則有Ki∈md(xj),否則Ki?md(xj)。

證明與定理4證明類似。

例5 (接例1)

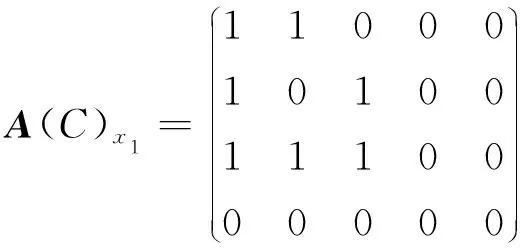
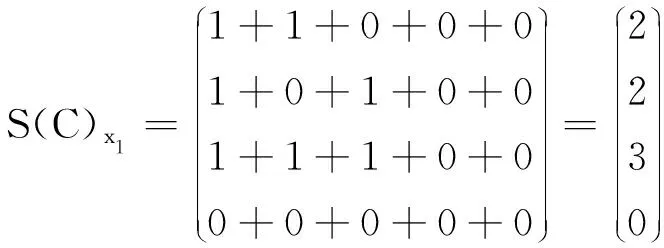
根據定理4和定理5,我們有md(x1)={K1,K2},MD(x1)={K3};

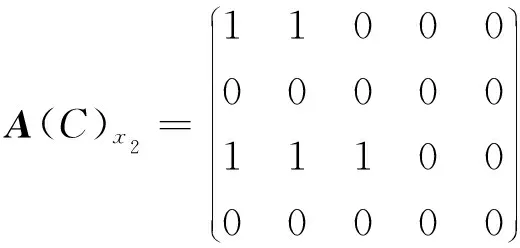
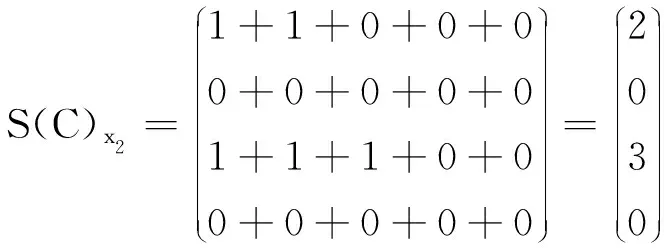
根據定理4和定理5,我們有md(x2)={K1},MD(x2)={K3};

因此md(x3)={K2},MD(x3)={K3};

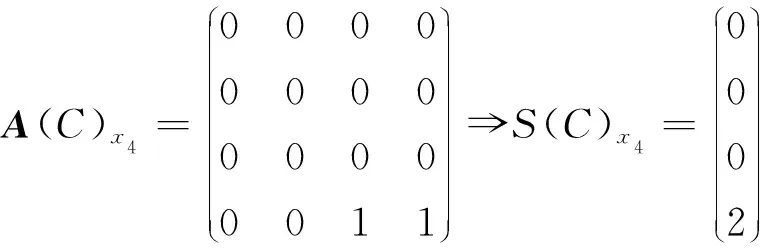
因此md(x4)={K4},MD(x4)={K4};

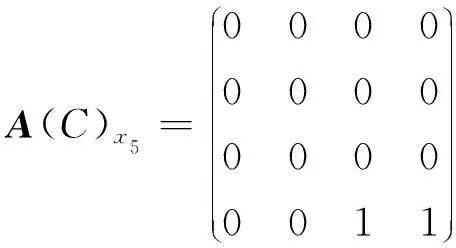
因此md(x5)={K4},MD(x5)={K4}。

通過例5我們可以發現,利用改進之后的矩陣方法也能求出最大和最小描述,而且改進方法計算簡單,僅僅只需要對A(C)xi中矩陣各行進行累加得到S(C)xi,然后再根據特征函數,計算就可以得到所需的最大和最小描述。與文獻[14]和文獻[15]中的方法相比,改進后的方法算法3不需要進行復雜的矩陣運算,時間復雜度降為O((|C||U|)。

算法3 改進后的計算最大和最小描述的LXW方法輸入:論域U={x1,…,xm}U上的一個覆蓋C={K1,…,Kn}A(C)=(aij)mn輸出:md(xj),MD(xj)Begin1:m←|U|∥輸入論域U2:n←|C|∥輸入論域C3: for i=1→n do4: for j=1→m do5: if xj∈Ki then aij=16: else aij=07: end if8: computeA(C)∥計算C的矩陣描述9: end for10: end for11: for j=1→m do12: for i=1→n do13: compute S(C)xj∥計算得到S(C)xj14: end for15: for i=1→n do16: if S(C)xj(i)=min([S(C)xj(i)]n×1>0)17: then g(md(xj)(i))←1,md(xj)←Ki∥計算得到最小描述18: else g(md(xj)(i))←019: end if20:if S(C)xj(i)=max([S(C)xj(i)]n×1>0)21: then h(MD(xj)(i))←1,MD(xj)←Ki∥計算得到最大描述22: else h(MD(xj)(i))←023: end if24: end for25:end for26:return md(xj),MD(xj)

3 實驗比較分析

為了進一步驗證新方法在時間復雜度、計算效率等方面的有效性,我們在Iris等6個UCI數據集(見表1)上進行了求最大、最小描述的比較實驗,由于我們的方法只能解決具有離散屬性的數據,我們使用Rosetta軟件(http:∥www.lcb.uu.se/tools/rosetta/)進行填充輸入一些缺失值,并將數值和連續屬性轉換為離散屬性。實驗環境為64位、英特爾(R)酷睿(TM)i5-4210U處理器、2.7 GHz、2 GB獨顯和8 GB內存的筆記本電腦,實驗軟件為Matlab R2019a。

將每個數據集樣本按照10%,20%,30%,…,90%,100%等比例取樣進行比較實驗,分別比較算法1、算法2、算法3的最大和最小描述的運行時間,實驗結果如圖1和圖2所示。

實驗采取的十次等比例分取樣比較實驗,即將原來的6個UCI數據集等比例劃分成60個大小不一的數據子集。在這60個數據子集上比較三種計算最大化描述和最小化描述的算法結果,分析如下:

第一,新方法(算法3)在Statlog,Chess,Bach Chorals Harmony 和 Anuran Calls(MFCCs)上的計算效率要明顯優于現有的兩種算法(文獻[9]與文獻[12]所提出的方法)。特別地,算法3在大數據集上的計算效果優勢更為顯著。第二,算法3比算法1的計算效果更好。而與算法2的比較過程中,在小數據集中出現計算時長高于算法2的情況,例如在Iris,German以及各大數據集中的部分小的子數據集,效果優勢不明顯,基于數據大小規模在70～1 699不等的數據集中,其計算效果始終與算法2的計算效果保持相近,但卻優于算法1。但當數據集大小超過1 699時,算法3的計算效率優勢較為明顯,即計算時長都要低于算法1與算法2。具體數據比較過程詳細請參見表2至表5,其中A1為算法1,A2為算法2,A3為算法3,運行時間之差分別為算法3的運行時間減去算法2的運行時間與算法3的運行時間減去算法1的運行時間。

綜上所述,實驗結果表明隨著數據集大小的不斷增加,新算法的運行時間明顯少于Wang方法的運行時間;在較大數據集的情況下,新算法的計算效率要明顯高于Liu方法。由此可以得出結論,改進后的算法,時間復雜度顯著降低,計算效率大大提高,更具有現實意義。

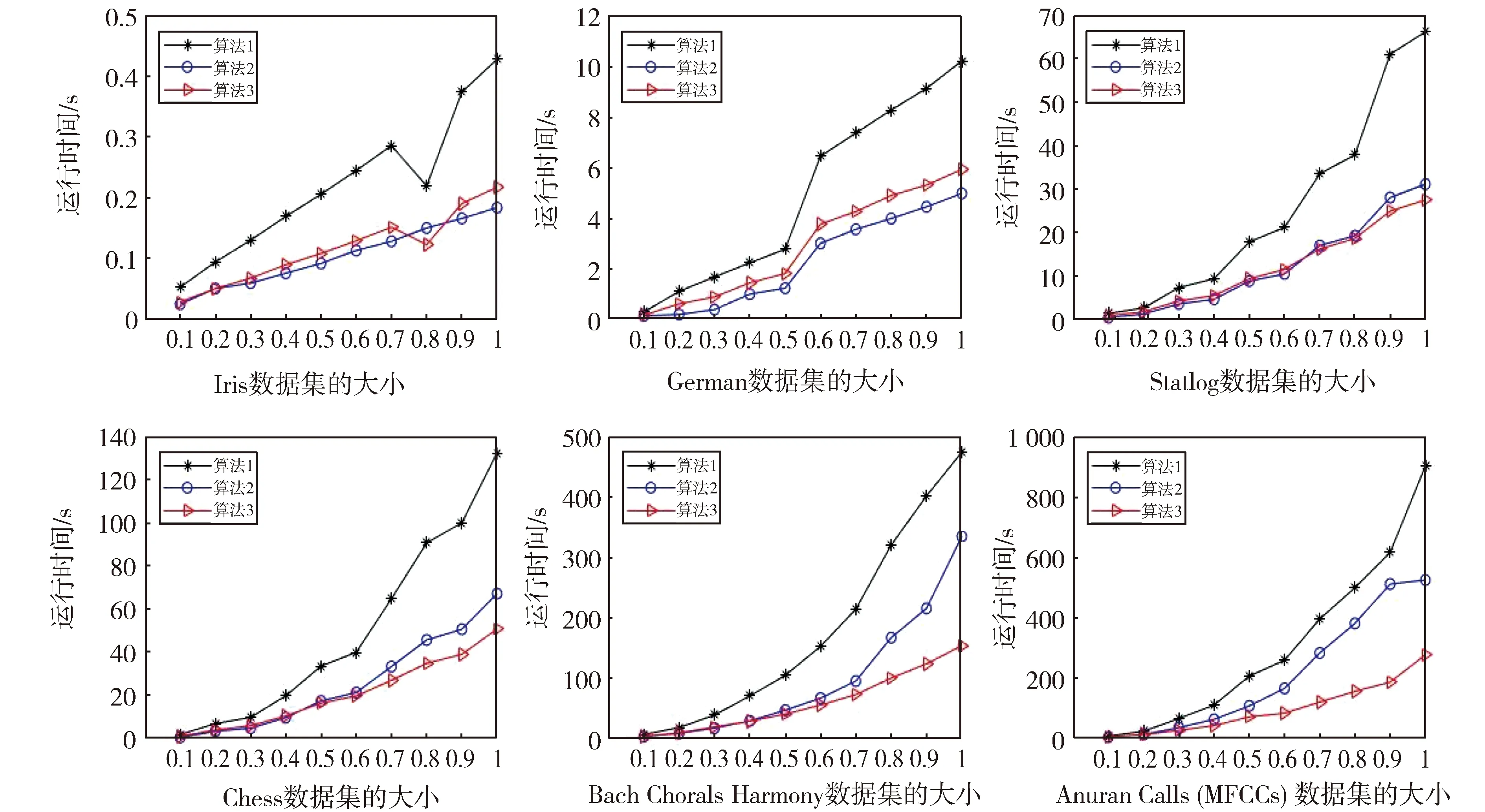
圖1 計算最小描述運行時間的比較Fig.1 Comparison of calculated min-description runtimes

表2 計算最小化描述運行時間之差(1)

表3 計算最小化描述運行時間之差(2)

表4 計算最大化描述運行時間之差(1)

4 結論

本文提出了一種計算最小描述和極大描述的改進方法。理論和實驗證明該方法不僅可以求得覆蓋粗糙集的最小描述和最大描述,還能簡化計算過程,節約計算時間。這為覆蓋粗糙集的最大和最小描述求解提供了新思路和新方法,為覆蓋粗糙集的進一步實際應用提供了技術支持。