富水隧道圍巖穩定性的數值模擬研究

孫學超

(中鐵十九局集團第三工程有限公司，遼寧 沈陽 110136)

0 引言

進行富水區隧道開挖時，經常會遇到突水突泥的情況。在富水區開挖隧道不僅需要考慮地下水對隧道力學參數的減損，同時還需要考慮流固耦合作用對隧道圍巖產生的力學效應。關于流固耦合作用對隧道圍巖穩定性的影響問題逐漸引起相關人員的關注。李術才等[1]開發了可用于模擬準三維平面應力和平面應變的新型流固耦合模型試驗系統，該系統既能保證試驗要求的密封性，又便于可視化觀察施工過程中海底隧道圍巖滲流、變形特征。采用該流固耦合模型試驗系統，以及獨立研制的新型流固耦合相似材料并依托青島膠州灣海底隧道開展流固耦合模型試驗研究，揭示海底隧道施工過程中洞壁壓力和圍巖位移場、滲流場等的變化規律。榮傳新等[2]應用統一強度理論和彈塑性損傷力學模型，推導出立井混凝土井壁彈性區和塑性損傷區應力的解析表達式，以及井壁承受的地下水壓與塑性損傷區半徑之間關系的解析表達式。單鵬飛等[3]通過位移反演方法對區域地應力特征進行理論分析，建立研究煤巖內部裂隙時空演化規律的力學實驗系統，設計了區域地應力作用下裂隙煤巖流固耦合計算模型，初步揭示裂隙煤巖流固耦合特性。姚多喜等[4]根據五溝煤礦1018工作面地質及水文地質條件，應用三維快速拉格朗日(FLAC-3D)流固耦合分析模塊，采用變滲透系數方法，對該工作面底板巖體采動滲流應變機制進行數值模擬研究。李順才等[5]利用承壓破碎巖石非Darcy滲流的滲透特性試驗規律,對破碎巖體滲流動力系統進行了應力場與滲流場耦合的分岔行為研究。

流固耦合作用對隧道圍巖的安全穩定性具有重要的影響。楊林地區地下水豐富，圍巖穩定性相對較差。本文采用MIDAS/GTS NX流固耦合模塊建立計算模型，分析研究流固耦合作用對圍巖應力場和位移場的影響規律，為隧道開挖后的支護條件提供可靠依據。

1 模型建立

隧址區地下水充足，巖性多樣，裂隙較發育，巖體多為碎裂狀，圍巖等級較低，穩定性差，隧道開挖時產生嚴重的變形。根據工程地質勘測資料顯示，隧道圍巖主要含大理巖、石灰巖、花崗巖以及混合巖等多種巖性的巖體。隧道橫斷面為馬蹄形，采用噴錨支護。

由于隧道軸向長度遠大于橫斷面尺寸，因此，在分析隧道應力場和位移場時僅對斷面方向進行研究。隧道寬度方向左右各取3倍洞跨，模型地邊界距離隧道底板2倍洞高，頂部取至地表，距離隧道拱頂140 m。計算模型及測點布設見圖1，圖中A點代表隧道底板測點，B點代表設定拱頂測點，C、D點分別代表隧道左右邊墻測點，E點代表地表沉降測點。計算參數見表1，模型計算參數均取自室內試驗。

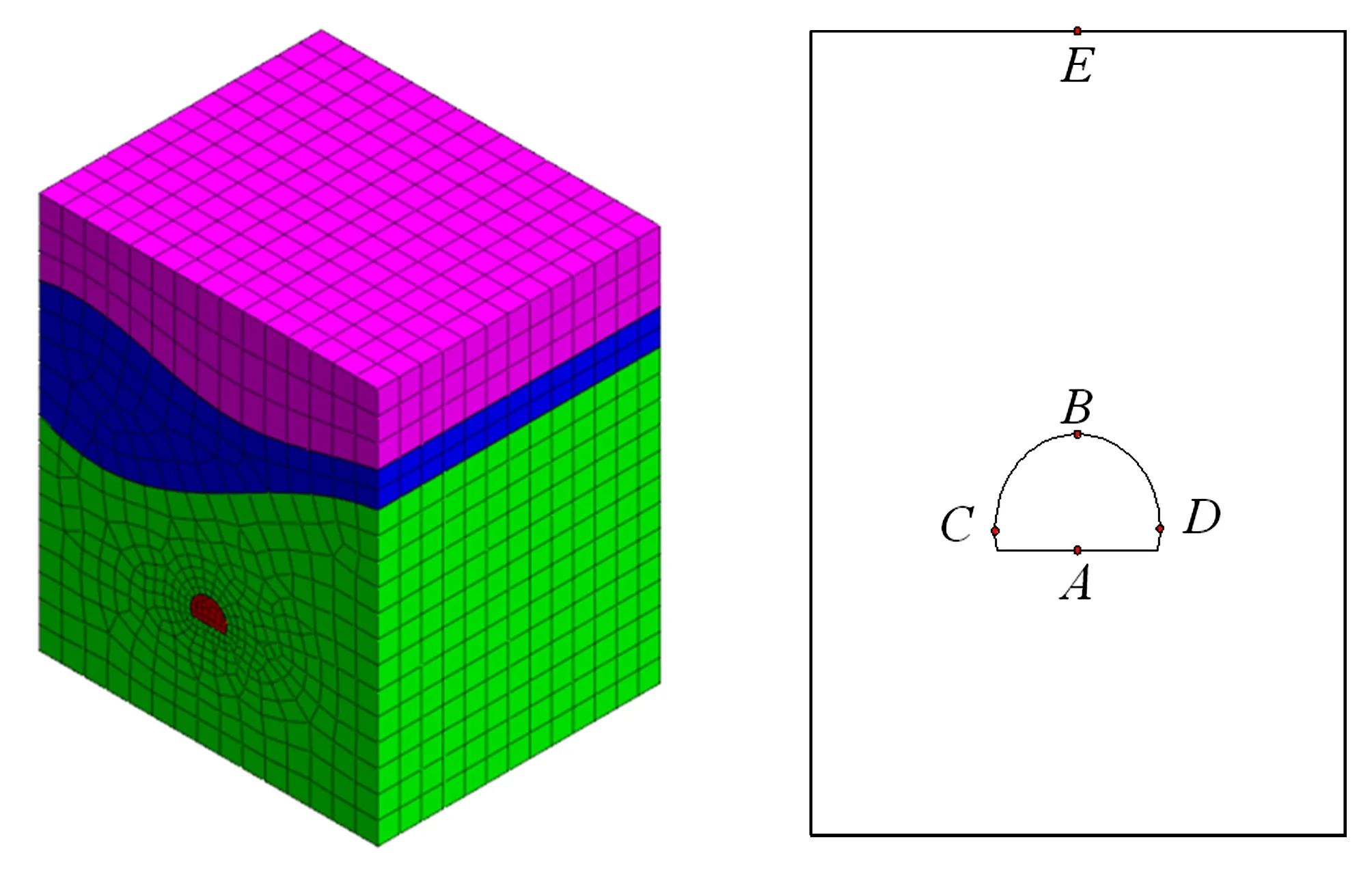
圖1 數值計算模型及測點布設

表1 模型計算參數

由于本文試驗參數均由Mohr-Columd強度準則計算得出，數值模擬過程中假定巖體為各向同性材料，地層之間的應力-應變關系均在彈性范圍內變化。根據連續介質力學中的位移邊界、應力邊界以及混合邊界條件的設定原則，模型左右兩側對水平方向位移進行約束，底面位移對數值方向進行約束，頂部為自由面。用模型進行流固耦合計算時，假設隧道開挖前各巖體均處于飽和狀態，滲流邊界水頭為距離隧道拱頂140 m位置，左右兩側和底部均假定為不透水邊界，設定孔隙水壓力值為零[6]。在隧道拱頂、底板、左右邊墻以及地表布設監測點，測點分布如圖所示，并與實際測量結果進行對比分析。

2 圍巖應力場分析

隧道開挖后，最大主應力分布如圖2所示，可以看出隧道周邊的應力場在有無滲流條件下均發生了應力重分布現象，且在隧道周邊區域較為明顯。其原因可能是由于隧道開挖后破壞了原有巖層的應力場，使隧道周邊圍巖向開挖面積聚。對比發現，無滲流條件下的最大主應力為5.72 MPa，滲流條件下的最大主應力為1.77 MPa，且滲流條件下整體最大主應力均較無滲流條件下小，其原因可能是由于地下水滲流作用使巖體自身強度減弱，加之開挖后裂隙擴大，滲流進入巖體內部的更多，致使巖體的最大主應力較小。因此，在地下水發育區域修建隧道等地下工程時，應及時進行支護或超前支護。

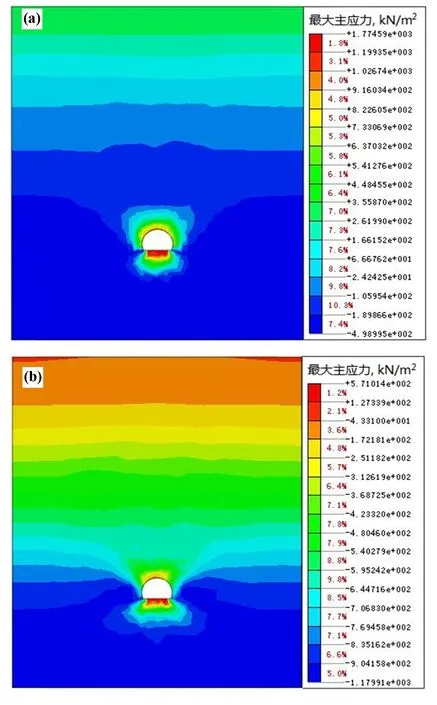
圖2 最大主應力分布云圖

滲流條件下，隧道開挖前和開挖后的孔隙水壓力等值線如圖3所示，可以看出，隧道開挖前，孔隙水壓力成層分布；開挖后，孔隙水壓力逐漸向隧道開挖面轉移，成漏斗狀分布，與實際情況類似。隧道開挖打破了原巖應力和孔隙水壓力的分布，使圍巖向隧道內部調整和轉移，同時形成開挖松動區，使松動區圍巖損傷產生裂隙，地下水在重力的作用下，沿開挖裂隙滲流，最終使得開挖形成臨空面。隧道開挖也導致開挖區域周邊的位置水頭迅速下降，滲流最終成漏斗狀分布。

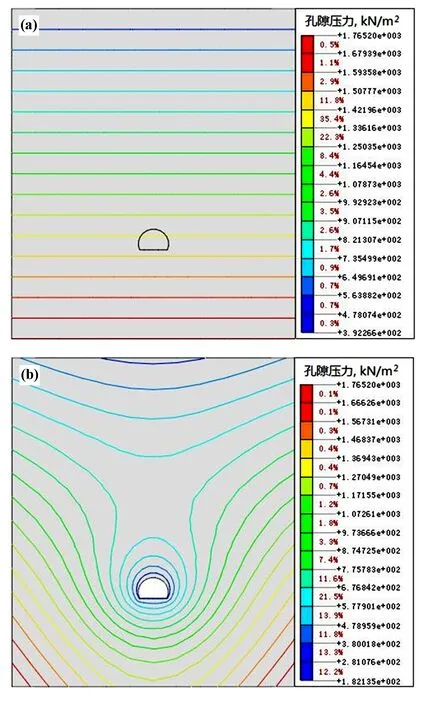
圖3 孔隙壓力等值線云圖

3 圍巖位移場分析

3.1 豎直方向位移分析

隧道開挖后，圍巖位移場豎直(Z)方向位移等值線如圖4所示，其中豎直向上為正值，豎直向下為負值，從圖中可以看出，滲流狀態下豎直方向的位移變化量明顯大于無滲流狀態的變化量，滲流情況下最大豎直方向位移值為72.27 mm，發生在隧道底板處，拱頂最大沉降為67.16 mm。無滲流狀態下最大豎直方向位移發生部位與滲流情況相同，其中隧道底板隆起值為61.03 mm，拱頂沉降值為59.21 mm。從位移分布等值線圖可以看出，滲流狀態下的整體沉降范圍大于無滲流狀態下的整體沉降。

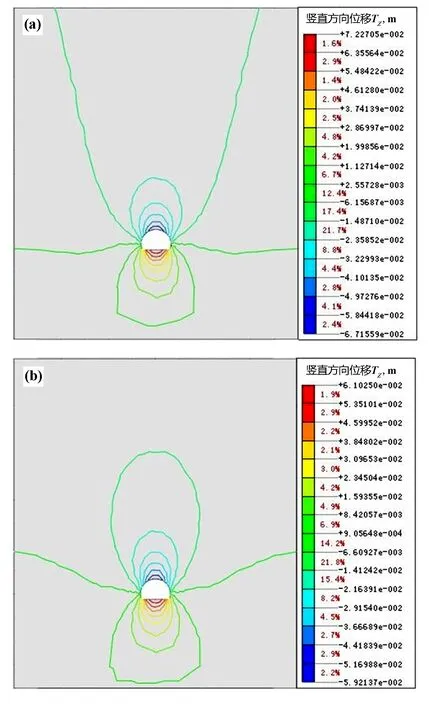
圖4 豎直方向(Z)位移等值線云圖

如圖5所示，分別為拱頂沉降和底板位移隨開挖時步變化曲線，根據現場實測數據與滲流和無滲流情況進行對比分析可知，隨著開挖時步的增加，拱頂沉降和底板位移均逐漸增大，并且逐漸趨于平緩，滲流狀態下拱頂和底板位移均大于無滲流狀態。現場實測數據與滲流狀態較為接近。現場條件復雜，操作流程、現場環境以及檢測儀器的誤差導致實測數據與滲流狀態下有些誤差。

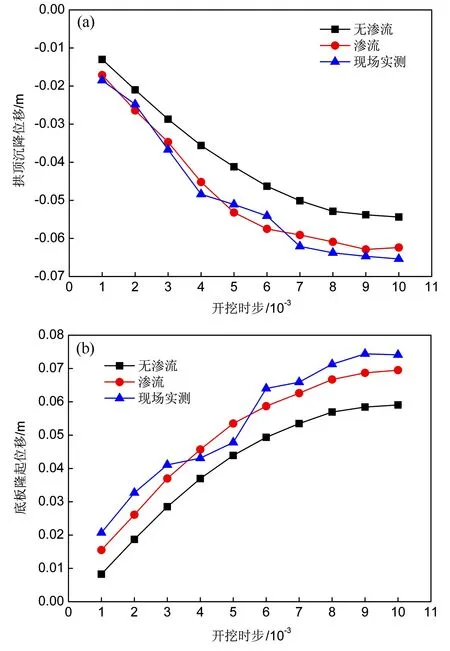
圖5 豎直方向(Z)位移曲線隨開挖時步分布曲線

3.2 水平方向位移分析

隧道開挖后，圍巖位移場水平(Z)方向位移等值線如圖6所示，其中水平向右為正值，水平向左為負值，滲流狀態下水平位移略大，但與無滲流狀態相比變化不大。滲流狀態下最大水平位移值為30.65 mm，發生在隧道左邊墻位置，右邊墻水平位移為30.58 mm，左右兩側水平位移均向隧道內部收斂，且大體成對稱分布。無滲流狀態下水平位移的總體變化情況與滲流狀態類似，左側邊墻最大水平位移為29.74 mm，右側邊墻最大水平位移為29.95 mm。

圖6 水平方向(X)位移等值線云圖

如圖7所示，分別為左邊墻和右邊墻水平位移隨開挖時步變化曲線，根據現場實測數據與滲流和無滲流情況進行對比分析可知，隨著開挖時步的增加，左邊墻與右邊墻收斂值均隨著開挖時步的增大而增加，并且逐漸趨于平緩。滲流狀態下的水平位移變化量略大于無滲流狀態，但變化并不明顯。現場實測數據與滲流狀態較為接近，因現場情況復雜，操作流程，現場環境以及檢測儀器的誤差導致實測數據與滲流狀態下有些誤差。

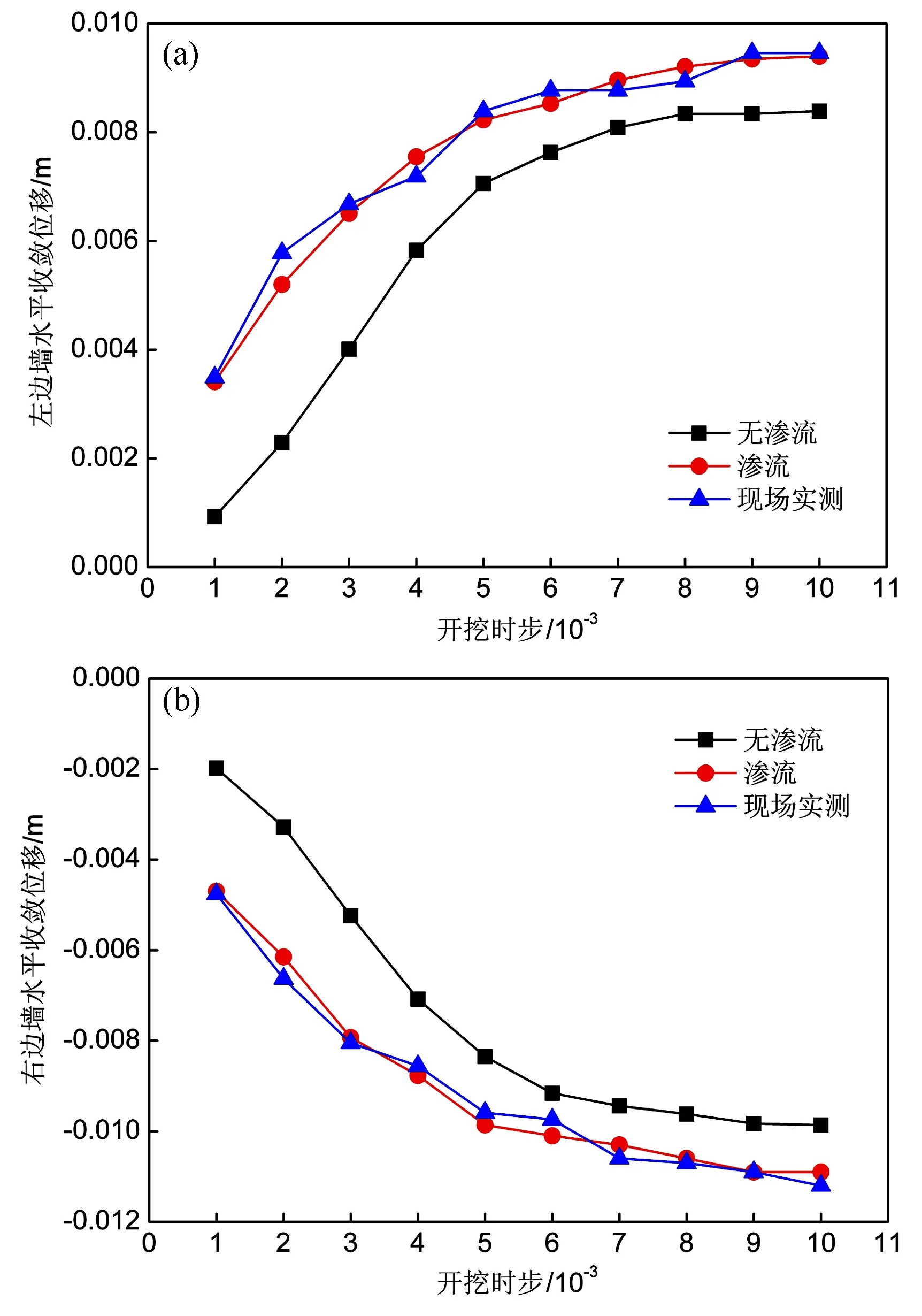
圖7 水平方向(X)位移隨開挖時步分布曲線

3.3 地表沉降分析

如圖8所示，地表沉降最大值位于隧道開挖中心處，整體呈漏斗狀塌陷，深流狀態較無滲流狀態變化明顯。在無滲流狀態下時，其原因可能是由于開挖導致拱頂下沉，隨之產生連帶反應，致使地表下沉。而滲流狀態更主要的原因是開挖導致大范圍內的孔隙水壓力減小所致。

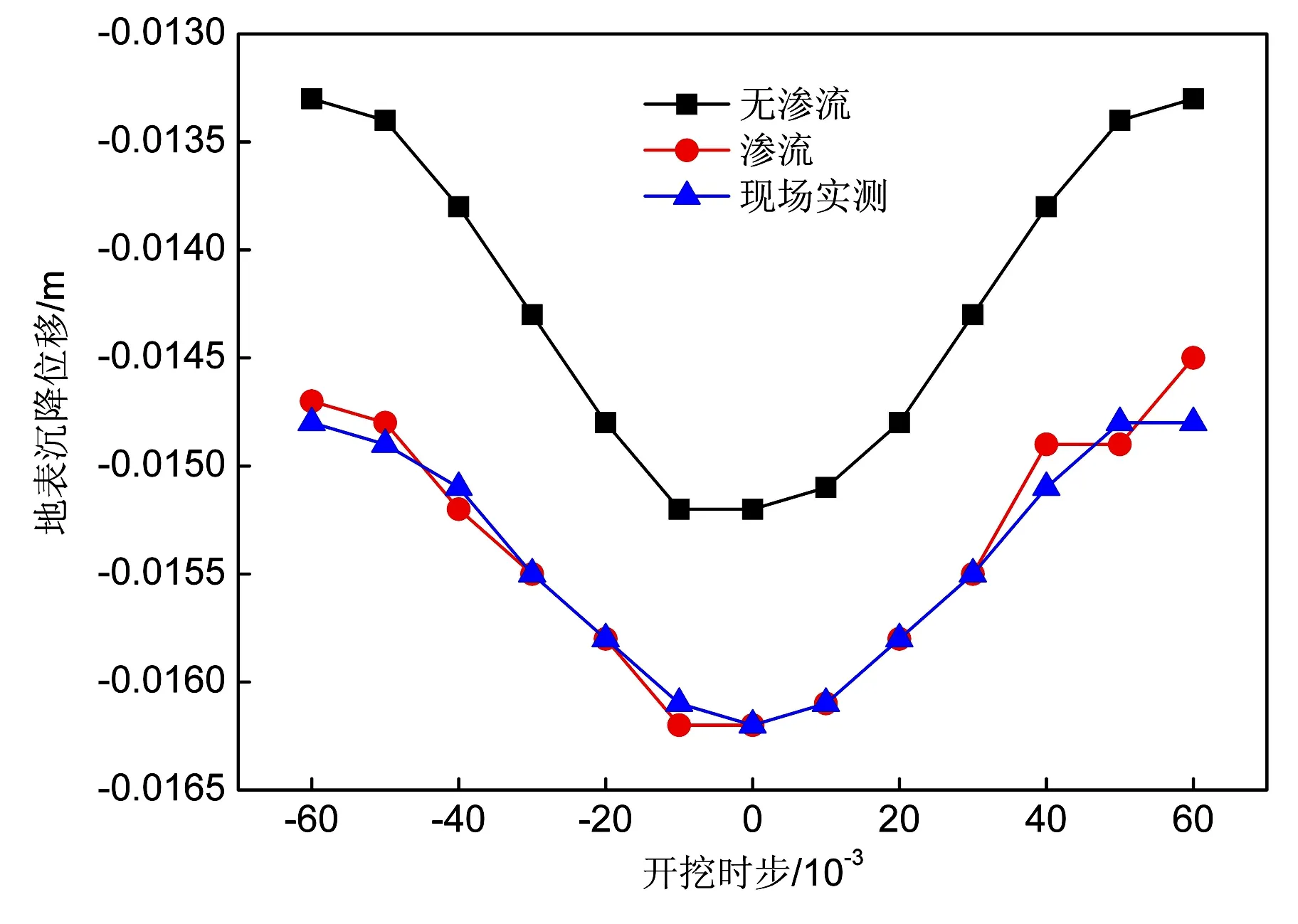
圖8 地表沉降距隧道中心位移

4 結論

通過對楊林隧道考慮流固耦合與不考慮流固耦合數值模擬研究以及實測數據對比分析得到如下結論：

(1)滲流作用下隧道周圍巖體應力重分布范圍較無滲流狀態下更大，由于水對巖體的滲流作用，導致巖體強度降低。滲流狀態下最大主應力明顯小于無滲流狀態下的最大主應力。由此可見，滲流作用將給隧道圍巖穩定性帶來不利影響。

(2)隧道圍巖變形研究可知，滲流作用對水平位移變化影響不大，其中滲流狀態略大于無滲流狀態。而滲流作用對豎直方向的位移變化情況影響較大，滲流作用下的拱頂沉降和底板隆起均明顯大于無滲流狀態。其中，隧道拱頂沉降位移從59.21 mm增加到61.75 mm，隧道底板隆起從61.03 mm增加到72.27 mm，左側隧道邊墻水平收斂從29.73 mm增加到30.64 mm，右側隧道邊墻水平收斂從29.95 mm增加到30.59 mm。

(3)根據地表沉降分析結果可知，在無滲流狀態下，可能是由于開挖導致拱頂下沉，隨之產生連帶反應，致使地表下沉，而滲流狀態更主要的原因是開挖導致大范圍內的孔隙水壓力減小所致。