基于相容關(guān)系的局部多粒度粗糙集模型

周悅麗,林國平*

(1.閩南師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,福建 漳州 363000;2.數(shù)字福建氣象大數(shù)據(jù)研究所,福建 漳州 363000)

0 引言

粗糙集理論是我們對于不確定信息進(jìn)行近似處理的一種模型。該理論[1]的主要內(nèi)容是通過不可分辨關(guān)系對信息系統(tǒng)進(jìn)行粒化，從而構(gòu)建目標(biāo)概念中有關(guān)樣本的上下近似集。

為了適應(yīng)社會(huì)的發(fā)展要求，粗糙集模型的推廣與應(yīng)用是許多學(xué)者討論和研究的重點(diǎn)。由經(jīng)典粗糙集的定義可以了解到經(jīng)典粗糙集是在等價(jià)關(guān)系的基礎(chǔ)上進(jìn)行定義的，且主要是面對屬性值完備且單一的信息系統(tǒng)，利用上下近似集來探尋信息系統(tǒng)中數(shù)據(jù)的相關(guān)性。但是實(shí)際應(yīng)用中，由于考慮到現(xiàn)實(shí)問題的復(fù)雜性、數(shù)據(jù)的不完整性與不精確性，許多學(xué)者通過擴(kuò)展等價(jià)關(guān)系建立了許多擴(kuò)展粗糙集模型，比如:建立鄰域關(guān)系和鄰域粗糙集模型[2-3]來處理數(shù)值型數(shù)據(jù);建立相容關(guān)系和相容類[4-5]來處理集值型的數(shù)據(jù)問題;建立容差關(guān)系和相似關(guān)系[6-7]等來處理缺失數(shù)據(jù)。此外，因?yàn)榻?jīng)典粗糙集模型的主要缺點(diǎn)是欠缺對噪聲數(shù)據(jù)和分類的容錯(cuò)能力，因此眾多學(xué)者將概率論與經(jīng)典粗糙集結(jié)合起來并進(jìn)行推廣，例如Pawlak建立了概率粗糙集模型[8],Ziako提出了變精度粗糙集模型[9]。同時(shí)在實(shí)際生活的應(yīng)用中，考慮到從不同角度觀察和分析同一問題，錢宇華等研究了多粒度粗糙集模型[10]。

大數(shù)據(jù)時(shí)代已經(jīng)到來，在監(jiān)督學(xué)習(xí)的策略下，經(jīng)典粗糙集及其擴(kuò)展模型需要大量標(biāo)記數(shù)據(jù)。面對大數(shù)據(jù)時(shí)代帶來的挑戰(zhàn)，標(biāo)記數(shù)據(jù)無疑會(huì)耗費(fèi)大量時(shí)間, 所以錢宇華提出了局部粗糙集模型[11]和局部多粒度決策粗糙集模型[12]。因?yàn)橐陨夏Ｐ途⒃诘葍r(jià)關(guān)系的基礎(chǔ)上，過于嚴(yán)格，不適用于其他數(shù)據(jù)類型。于是,Wang等人提出了局部鄰域粗糙集模型[13],Zhang等人在有序信息系統(tǒng)上建立了基于優(yōu)勢關(guān)系的局部粗糙集和局部多粒度決策粗糙集[14]。為了處理集值型的數(shù)據(jù)問題,Xu等人提出了兩類基于相容關(guān)系的多粒度粗糙集模型[15]。當(dāng)這兩類模型在處理數(shù)據(jù)的時(shí)候，要通過預(yù)覽整個(gè)論域中全部樣本的相容類才能進(jìn)行處理，這樣的處理方式在面對海量數(shù)據(jù)時(shí)，其效率比較低。于是本文在文獻(xiàn)[15]的基礎(chǔ)上，在集值信息系統(tǒng)上建立兩類局部多粒度相容粗糙集模型，進(jìn)一步有效處理此類數(shù)據(jù)，這樣可以把我們篩選的信息范圍縮小至局部，排除那些與目標(biāo)概念完全無關(guān)的全局中冗余的信息，減少時(shí)間的消耗和簡化計(jì)算步驟。

基于以上分析，本文首先基于集值信息系統(tǒng)給出局部多粒度相容粗糙集模型的定義，并探討了該模型的有關(guān)性質(zhì), 然后給出下近似的算法，并通過具體實(shí)例說明算法的有效性。

1 相關(guān)基礎(chǔ)知識

如果一個(gè)系統(tǒng)不是一個(gè)單值信息系統(tǒng),那么稱之為集值信息系統(tǒng)。其定義如下:

定義2[16]設(shè)S=(U，AT，V，f)為一個(gè)集值信息系統(tǒng),U為論域,AT是屬性集,V為值域,f是U×AT到V的映射,而且滿足以下條件f:U×AT→2V是一個(gè)集值映射。在此條件下，?a∈AT，x∈U,|f(x,a)|≥1。

定義3[4-5]設(shè)S=(U,AT,V,f)為一個(gè)集值信息系統(tǒng),?b∈AT,相容關(guān)系Tb定義如下:

Tb={(x,y)|f(x,b)∩f(y,b)≠?}。

(1)

對?B?AT,相容關(guān)系TB定義為:

TB={(x,y)|?b∈B,f(x,b)∩f(y,b)≠?}

即

(2)

當(dāng)(x,y)∈TB,則x與y是不可分辨的或x與y是相容的。

定義TB(x)={y|y∈U,yTBx},則TB(x)為x在TB下對象x的相容類。

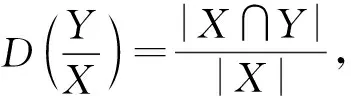
2 局部多粒度相容粗糙集模型

在現(xiàn)實(shí)中,集值型的數(shù)據(jù)問題比較常見,比如當(dāng)我們在對一個(gè)項(xiàng)目進(jìn)行投資之前,我們可以通過多位專家對項(xiàng)目的評價(jià)指標(biāo)進(jìn)行評估,這些評價(jià)指標(biāo)可以是收入、風(fēng)險(xiǎn)、社會(huì)效益、市場效應(yīng)等方面,當(dāng)不同的專家依次對各項(xiàng)指標(biāo)作出評價(jià)時(shí),可以得到對應(yīng)的評價(jià)意見。而將這些評價(jià)意見結(jié)合起來,這些不同意見也就成為對應(yīng)指標(biāo)的可能取值。因?yàn)槲墨I(xiàn)[10]中定義的多粒度粗糙集模型是在完備信息系統(tǒng)上提出的,對于集值信息系統(tǒng)上出現(xiàn)的集值型數(shù)據(jù),很顯然這些多粒度粗糙集模型并不適用。因此為了對比研究,在文獻(xiàn)[15]的基礎(chǔ)上,將論域U上第1型多粒度相容粗糙集模型和第2型多粒度相容粗糙集模型進(jìn)行推廣,提出集值信息系統(tǒng)上的樂觀多粒度相容粗糙集模型和悲觀多粒度相容粗糙集模型。

定義5 設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…，Tm(x),則X基于相容關(guān)系Ti,i=(1,2,…,m)的樂觀下近似和樂觀上近似分別為:

(3)

(4)

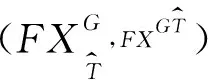
定義6 設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…,Tm(x),則X基于相容關(guān)系Ti,i=(1,2,…,m)的悲觀下近似和悲觀上近似分別為:

(5)

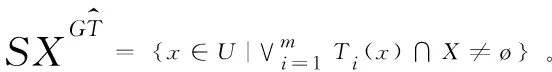
(6)

為了區(qū)分這兩種模型和接下來我們構(gòu)建的兩種模型,下文稱以上的樂觀多粒度相容粗糙集為全局樂觀多粒度相容粗糙集,悲觀多粒度相容粗糙集為全局悲觀多粒度相容粗糙集。

將局部粗糙集與多粒度相容粗糙集模型結(jié)合起來,建立以下兩種局部多粒度相容粗糙集,分別是局部樂觀多粒度相容粗糙集模型和局部悲觀多粒度相容粗糙集模型。

2.1 局部樂觀多粒度相容粗糙集模型

首先討論基于m種相容關(guān)系的局部樂觀多粒度相容粗糙集。

定義7 設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…,Tm(x),則X基于相容關(guān)系Ti,i=(1,2,…,m)的局部α-樂觀下近似和局部β-樂觀上近似分別為:

(7)

D(X/Ti(x))>β,x∈X}。

(8)

當(dāng)α=1,β=0時(shí),

D(X/Ti(x))>0,x∈X}=

從上述分析可知,當(dāng)α=1,β=0時(shí),局部樂觀多粒度相容粗糙集模型可退化為全局樂觀多粒度相容粗糙集模型,也就是說,局部樂觀多粒度相容粗糙集與全局樂觀多粒度相容粗糙集具有相同的形式與語義。從這個(gè)角度來看,這兩種模型具有一致的處理集值型數(shù)據(jù)的能力。因此,我們可以把全局樂觀多粒度相容粗糙集模型看作是局部樂觀多粒度相容粗糙集模型的一種特殊情形。

下面給出局部樂觀多粒度相容粗糙集的相關(guān)性質(zhì)及其證明。

性質(zhì)1設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…,Tm(x),則對于任意的X,Y?U,0≤β<α≤1,有以下性質(zhì)成立：

證明

(2)β∈[0,min{D(X/Ti(x)):

(3)a)|Ti(x)∩?|=0

?D(?/Ti(x))=0,?i≤m

?D(?/Ti(x))≤β<α,?i≤m

b)Ti(x)∩U=Ti(x)

?D(U/Ti(x))=1,?i≤m

?D(U/Ti(x))≥α>β,

?i≤m(0≤β<α≤1)

(4)X?Y

?D(X/Ti(x))≤D(Y/Ti(x)),?i≤m

??i≤m,s.t.D(Y/Ti(x))≥D(x|Ti(x))≥α

D(Y/Ti(x))≤D(Y|Ti(x))≤β

??i≤m,s.t.D((X∩Y)/Ti(x))≥α

??i≤m,s.t.D(X/Ti(x))≥α,

??i≤m,s.t.D((X∪Y)/Ti(x))≤β

??i≤m,s.t.D(X/Ti(x))≤β,

??i≤m,s.t.D(X/Ti(x))≥αor

D(Y/Ti(x))≥α

??i≤m,s.t.D(X∪T)/Ti(x))≥α

??i≤m,s.t.D(X∩Y/Ti(x))≤βor

D(Y/TB(x))≤β??i≤m,s.t.D((X∩Y)/Ti(x))≤β

??i≤m,s.t.D(X/Ti(x))≥α2

??i≤m,s.t.D(X/Ti(x))≥α1

??i≤m,s.t.D(X/Ti(x))≤β1

??i≤m,s.t.D(X/Ti(x))≤β2

2.2 局部悲觀多粒度相容粗糙集模型

定義8 設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…，Tm(x),則X基于相容關(guān)系Ti,i=(1,2,…,m)的局部α-悲觀下近似和局部β-悲觀上近似分別為:

D(X/Ti(x))≥α,x∈X},

(9)

D(X/Ti(x))>β,x∈X}。

(10)

性質(zhì)2設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…，Tm(x),則對于任意的X，Y?U，0≤β≤α≤1,有以下性質(zhì)成立:

(2)β∈[0,min{D(X/Ti(x)),

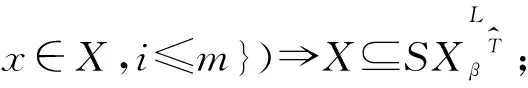
(7)0.5<α1<α2≤1

(8)0≤β1<β2<0.5

局部樂觀多粒度相容粗糙集和局部悲觀多粒度相容粗糙集聯(lián)系的分析：

定理1 設(shè)S=(U，AT，V，f)是一個(gè)集值信息系統(tǒng),T1,T2,…,Tm為論域U上的m個(gè)相容關(guān)系,由T1,T2,…,Tm誘導(dǎo)出的相容類為T1(x),T2(x),…，Tm(x),且X?U，則我們可以得到:

其實(shí),局部悲觀多粒度相容粗糙集模型和局部樂觀多粒度相容粗糙集模型類似。在一定條件下,也可以退化為全局悲觀多粒度相容粗糙集模型。因此,可以看出兩種局部多粒度相容粗糙集模型在本質(zhì)上并沒有改變兩種全局多粒度相容粗糙集模型。不過,在兩種局部多粒度相容粗糙集模型中,計(jì)算目標(biāo)概念的下、上近似不需要事先獲取論域中全部樣本的相容類,而只需要計(jì)算目標(biāo)概念中樣本的相容類,這大大減少了計(jì)算的時(shí)間。接下來用相關(guān)算法和例子分析對此進(jìn)行具體說明。

3 算法

與全局多粒度相容粗糙集模型進(jìn)行比較,可以發(fā)現(xiàn)局部多粒度相容粗糙集模型在對下近似的計(jì)算中效率較高,在這里給出局部樂觀多粒度相容粗糙集和全局樂觀多粒度相容粗糙集的下近似算法,并進(jìn)行比較。

算法1給定集值信息系統(tǒng)中的局部樂觀多粒度相容粗糙集的目標(biāo)概念的下近似

輸入：集值信息系統(tǒng)S=(U，AT，V，f)和目標(biāo)概念X?U以及參數(shù)α

輸出：目標(biāo)概念的局部下近似LLA。

1: 從i=1到m

從j=1到|X|進(jìn)行循環(huán)運(yùn)算,計(jì)算出xi的相容類Ti(xj)。

2:LLA??,j=1;

3: 從j=1到|X|做循環(huán)

{

如果∪D(X/Ti(xj))≥α,i=1,2,…,m

然后LLA?LLA∪{xj}

}

4. 返回LLA,算法結(jié)束。

算法2給定集值信息系統(tǒng)中的全局樂觀多粒度相容粗糙集的目標(biāo)概念的下近似

輸入：集值信息系統(tǒng)S=(U，AT，V，f)和目標(biāo)概念X?U以及參數(shù)α

輸出：目標(biāo)概念的全局下近似GLA.

1: 從i=1到m

從j=1到|U|進(jìn)行循環(huán)運(yùn)算,計(jì)算出xi的相容類Ti(xj)。

2:GLA??,j=1;

3: 從j=1到|U|做循環(huán)

{

如果∪D(X/Ti(xj))=1,i=1,2,…,m

然后GLA?GLA∪{xj}

}

4: 返回GLA,算法結(jié)束。

在算法1中只需要計(jì)算X中每個(gè)樣本在m個(gè)相容關(guān)系下的相容類，因此它的時(shí)間復(fù)雜度包括算法1中的步驟1，步驟3和其他步驟的時(shí)間復(fù)雜度。設(shè)其他步驟時(shí)間復(fù)雜度為常數(shù)，即計(jì)算其下近似的時(shí)間復(fù)雜度等于O(|m||X||U|)+O(|m||X|2)+常數(shù);在算法2中需要計(jì)算U中每個(gè)樣本在m個(gè)相容關(guān)系下的相容類，因此它的時(shí)間復(fù)雜度包括算法2中的步驟1，步驟3和其他步驟的時(shí)間復(fù)雜度，即O(|m||U|2)+O(|m||X||U|)+常數(shù)。

證明根據(jù)以上分析，可以得到:

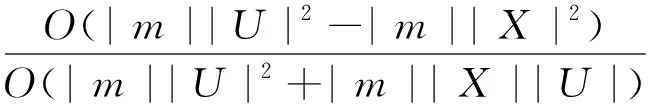
基于以上理論分析,可以得到局部多粒度下近似算法在處理大規(guī)模數(shù)據(jù)時(shí)是十分高效的。從上述結(jié)果看出時(shí)間效率t提升和時(shí)間節(jié)約率p均隨著論域U的增大而增大,U越大,算法1相比算法2越高效。

4 例子分析

通過一個(gè)例子來說明以上的有關(guān)概念，給定一個(gè)集值信息系統(tǒng)，如表1所示。

表1 集值信息系統(tǒng)

在S=(U,AT,V,f)中,取A={a1,a2},B={a2,a3},和C={a3,a4}為AT的屬性子集,這三個(gè)屬性子集可以確定論域U上三個(gè)相容關(guān)系,分別記為T1,T2和T3,對于給定目標(biāo)概念X={x1,x3,x4,x8,x9},取α=0.6,β=0.1,若計(jì)算X的局部樂觀多粒度相容粗糙集下、上近似,我們只需要計(jì)算X中樣本的相容類,通過定義計(jì)算可得:

T1(x1)={x1,x2,x3,x4},

T1(x3)={x1,x3},

T1(x4)={x1,x2,x4,x6,x7,x8,x9},

T1(x8)={x2,x4,x6,x8},

T1(x9)={x2,x4,x5,x6,x7,x9},

T2(x1)={x1,x2,x3,x4,x6},

T2(x3)={x1,x2,x3,x4,x6},

T2(x4)={x1,x2,x3,x4,x5,x6,x7,x8,x9},

T2(x8)={x2,x4,x6,x8},

T2(x9)={x2,x4,x7,x9},

T3(x1)={x1,x2,x3,x4,x6,x8},

T3(x3)={x1,x2,x3,x4,x6,x8},

T3(x4)={x1,x2,x3,x4,x5,x6,x7,x8,x9},

T3(x8)={x1,x2,x3,x4,x6,x8},

T3(x9)={x2,x4,x7,x9}。

因此根據(jù)包含度公式可得:

{D(X/T1(xn),n=1,3,4,8,9}=

{D(X/T2(xn),n=1,3,4,8,9}=

{D(X/T3(xn),n=1,3,4,8,9}=

由α=0.6,β=0.1可得:

對于全局樂觀多粒度相容粗糙集，需要計(jì)算全部樣本的相容類，通過計(jì)算可以得到:

T1(x1)={x1,x2,x3,x4},

T1(x2)={x1,x2,x4,x6,x7,x8,x9},

T1(x3)={x1,x3},

T1(x4)={x1,x2,x4,x6,x7,x8,x9},

T1(x5)={x5,x6,x7,x9},

T1(x6)={x2,x4,x5,x6,x7,x8,x9},

T1(x7)={x2,x4,x5,x6,x7,x9},

T1(x8)={x2,x4,x6,x8},

T1(x9)={x2,x4,x5,x6,x7,x9},

T2(x1)={x1,x2,x3,x4,x6},

T2(x2)={x1,x2,x3,x4,x6,x7,x8,x9},

T2(x3)={x1,x2,x3,x4,x6},

T2(x4)={x1,x2,x3,x4,x5,x6,x7,x8,x9},

T2(x5)={x4,x5,x6},

T2(x6)={x1,x2,x3,x4,x5,x6,x8},

T2(x7)={x2,x4,x7,x9},

T2(x8)={x2,x4,x6,x8},

T2(x9)={x2,x4,x7,x9},

T3(x1)={x1,x2,x3,x4,x6,x8},

T3(x2)={x1,x2,x3,x4,x6,x7,x8,x9},

T3(x3)={x1,x2,x3,x4,x6,x8},

T3(x4)={x1,x2,x3,x4,x5,x6,x7,x8,x9},

T3(x5)={x4,x5,x6},

T3(x6)={x1,x2,x3,x4,x5,x6,x8}

T3(x7)={x2,x4,x7,x9},

T3(x8)={x1,x2,x3,x4,x6,x8},

T3(x9)={x2,x4,x7,x9}。

由包含度公式可得:

{D(X/T1(xn),n=1,2,3,4,5,6,7,8,9}=

{D(X/T2(xn),n=1,2,3,4,5,6,7,8,9}=

{D(X/T3(xn),n=1,2,3,4,5,6,7,8,9}=

由定義可得:

在例子中,我們可以看到計(jì)算目標(biāo)概念X的上下近似時(shí),局部樂觀多粒度相容粗糙集只需要計(jì)算15個(gè)相容類。然而,全局樂觀多粒度相容粗糙集則需要計(jì)算27個(gè)相容類。從這里可以看出,就計(jì)算相容類的個(gè)數(shù)而言,局部多粒度相容粗糙集降低了計(jì)算目標(biāo)概念X的上下近似的時(shí)間。

集值型數(shù)據(jù)的研究頗具實(shí)際意義,比如在對投資項(xiàng)目進(jìn)行風(fēng)險(xiǎn)評估時(shí),通過綜合不同專家對于各項(xiàng)評估指標(biāo)的評價(jià)意見,會(huì)降低投資失敗的風(fēng)險(xiǎn),爭取利益最大化。由以上例子可以看出,局部多粒度相容粗糙集模型處理集值型的數(shù)據(jù)問題時(shí)能夠提高計(jì)算效率,減少計(jì)算量。