四索股吊索尾流致振節段模型測振試驗研究

李壽英，張明哲, 2，鄧羊晨, 2，陳政清, 2

四索股吊索尾流致振節段模型測振試驗研究

李壽英1，張明哲1, 2，鄧羊晨1, 2，陳政清1, 2

(1. 湖南大學 風工程與橋梁工程湖南省重點實驗室，湖南 長沙 410082；2.湖南大學 土木工程學院，湖南 長沙 410082)

為研究大跨度懸索橋四索股吊索尾流致振現象，針對鋼絲繩吊索和平行鋼絲吊索，分別制作表面粗糙和表面光滑的圓柱節段模型，并進行四索股吊索尾流致振節段模型測振風洞試驗。試驗測得不同雷諾數、風攻角下尾流索股的風致振動響應，研究其隨風速的變化規律，分析發生大幅振動時的起振風速、振幅、運動軌跡、時程及振動頻率，并研究了阻尼比對四索股吊索尾流致振的影響。研究結果表明：光滑和粗糙尾流圓柱發生尾流致振的最不利攻角均在70°左右，但光滑圓柱的起振風攻角范圍更寬；在70°風攻角下，2類尾流圓柱的穩定振動軌跡均為順時針橢圓，但光滑尾流圓柱發生尾流致振時的氣動負剛度效應更加強烈；當阻尼比增大到0.67%時，可對粗糙圓柱的尾流致振起到很好的控制效果。

四索股吊索；風洞試驗；尾流致振；風攻角；阻尼比；振動頻率

懸索橋吊索長細比大、頻率低、阻尼小，常易發生風致振動現象[1]，如丹麥大帶東橋、日本明石海峽大橋及我國的舟山西堠門大橋均出現相關報道[2?4]。懸索橋吊索常由多根索股組成，在風的作用下索股之間將產生氣動干擾，尤其多根索相鄰布置時下游索通常會受上游索尾流的影響而發生尾流致振現象。懸索橋吊索的風致振動本質上屬于存在流體介質內的多圓柱繞流及彈性振動問題，國內外學者對多圓柱間的氣動干擾現象進行了系統的研究。Zdravkovich[5]在對不同排列方式的雙圓柱進行大量實驗的基礎上，將2個圓柱之間的氣動干擾分為3種類型。Kitagawa等[6]則采用數值計算方法研究了亞臨界雷諾數下串列雙圓柱之間的流態，討論了不同間距比下，上游圓柱尾流對下游圓柱的動力影響。Fujino等[7]采用足尺節段模型研究了2根和3根并列拉索模型的尾流致振發生條件和振動控制措施。Yagi等[8]進行單自由度和雙自由度自由振動試驗，將尾流致振現象分為尾流馳振和尾流顫振兩種類型。李永樂等[9]通過風洞測振試驗研究了遠距失穩區拉索尾流馳振現象，分析了拉索間距、風向角等對下游索振動特性的影響。杜曉慶等[10]分別在亞臨界和臨界雷諾數區域內研究了雙圓柱的平均氣動性能，發現在臨界雷諾數區域具有明顯的雷諾數效應。肖春云等[11]進行了鋼絲繩和平行鋼絲吊索的測力實驗，并對懸索橋雙吊索尾流致振的失穩區間進行研究；鄧羊晨等[12]則比較研究了鋼絲繩和平行鋼絲吊索的氣動特性。在上述試驗數據的基礎上，LI等[13?14]分別建立了準定常和非定常吊索尾流致振節段理論模型，均數值重現了吊索尾流致振現象；LI等[15]則進一步建立了吊索尾流致振三維連續理論模型。以上關于圓柱之間氣動干擾的研究多集中在最基本的雙圓柱，而如今隨著懸索橋跨徑的不斷增大，騎跨式四索股吊索得到越來越多的應用。由于多圓柱之間的氣動干擾具有高度的非線性，疊加原理并不適用，所以有必要對四索股吊索的氣動干擾現象進行研究。本文以西堠門大橋2號吊索的結構參數為工程背景，進行了矩形排列的四索股吊索的節段模型尾流致振風洞試驗，研究了在雷諾數0.2×105～1.2×105，風攻角0°～90°范圍內尾流索股風致振動響應，分析了尾流索股發生大幅振動時的起振風速、振幅、運動軌跡、時程及振動頻率，并對阻尼比的影響進行了研究。

1 風洞試驗概況

以西堠門橋2號吊桿的結構參數為工程背景，該吊桿包括4根鋼絲繩索股，直徑為=0.088 m，索股橫橋向中心間距為7.0,順橋向中心間距為3.5。采用粗糙圓柱和光滑圓柱來分別模擬懸索橋鋼絲繩和平行鋼絲吊索。其中，粗糙圓柱由尼龍繩纏繞制作，光滑圓柱采用PVC圓管。幾何縮尺比為1:1，2類圓柱模型直徑均為=0.088 m。試驗中，3根圓柱模型固定在移測架上，另一根尾流中圓柱模型由4根彈簧懸掛。為減小端部效應影響，3根固定的圓柱模型長1.54 m，彈性懸掛的尾流圓柱模型長1.33 m。彈性懸掛圓柱質量為5.4 kg/m，頻率在1.66～1.70 Hz之間，粗糙圓柱阻尼比為0.20%和0.67%，光滑圓柱為0.24%。在試驗過程中，彈性懸掛圓柱模型保持空間位置不變，采用移測架移動3根固定圓柱模型的位置和角度來調整試驗工況。4根圓柱模型的空間位置采用相對間距和風攻角來定義，如圖1所示。其中，圓柱模型之間的相對間距與西堠門橋2號吊桿完全相同，=7.0，=3.5；風攻角范圍為=0°～90°，攻角間隔=10°。試驗在均勻流場中進行，風速范圍=1～20 m/s，風速間隔=1 m/s，對應的雷諾數范圍為0.238× 105～1.189×105。具體試驗參數如表1所示，圓柱模型安裝在風洞中的照片如圖2所示。

試驗在湖南大學HD-2風洞試驗室的高速試驗段進行，該試驗段寬3 m，高2.5 m，長17 m，風速在0～58 m/s范圍內連續可調。風速采用澳大利亞TFI公司的眼鏡蛇風速儀測量。分別采用2個加速度傳感器測量尾流彈性懸掛圓柱順風向和橫風向振動響應。其中，加速度傳感器采樣頻率為1 000 Hz，采樣時間60 s。獲得加速度信號后，用頻譜轉化法得到尾流圓柱的位移響應時程。

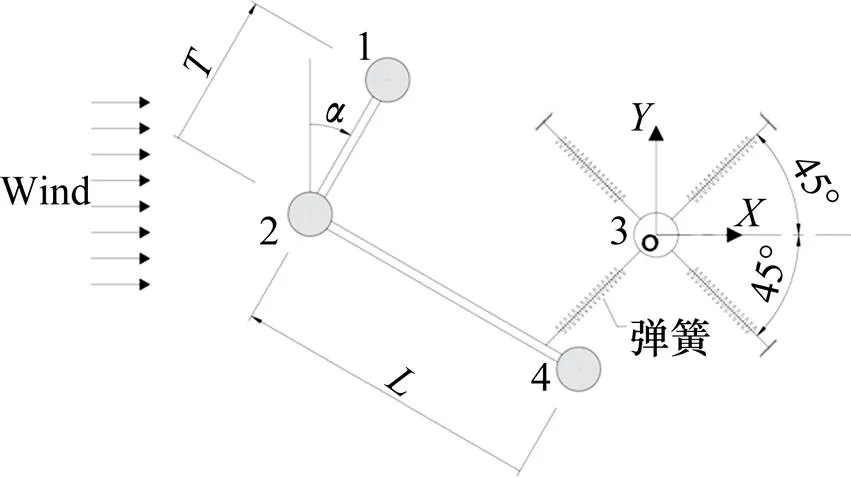
圖1 圓柱模型空間位置和風攻角定義

圖2 試驗模型在風洞中的安裝照片

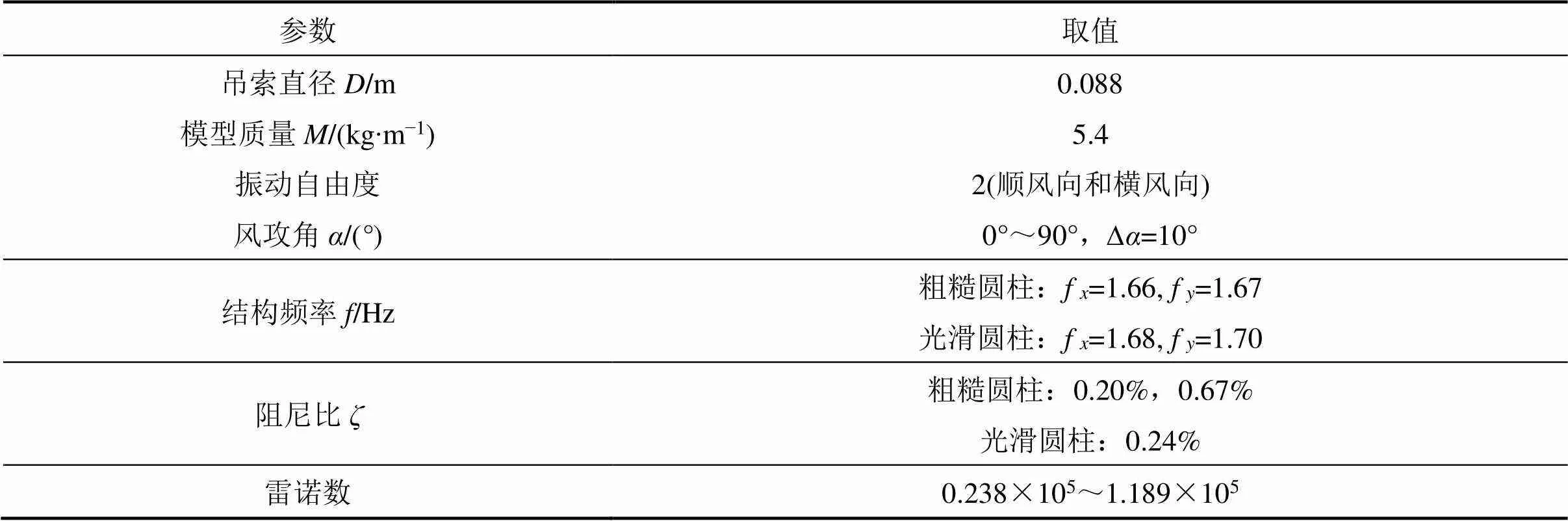
表1 風洞試驗參數

2 試驗結果與分析

2.1 吊索振幅隨風速變化規律

圖3給出了不同風攻角下、粗糙尾流圓柱振幅隨折減風速的變化曲線。其中，模型的結構阻尼比為=0.20%。從圖3可以看出，在0°～90°風攻角范圍內，僅當風攻角=70°時出現了大幅振動，起振折減風速為=82(=12 m/s)。風速達到起振風速后，隨著風速的進一步增加，粗糙尾流圓柱的順風向振幅急劇增長，呈明顯發散狀態；但橫風向振幅增長較為緩慢，甚至慢慢趨于穩定振幅。因此在起振初期(=82～96，振幅小于0.52)，尾流圓柱的橫風向振幅稍大于順風向振幅。但隨著風速繼續增大(＞102)，順風向振幅超過橫風向振幅，尾流圓柱表現為以順風向為主的大幅振動。當折減風速達到137時，順風向振幅約為3，橫風向振幅約為1.1。

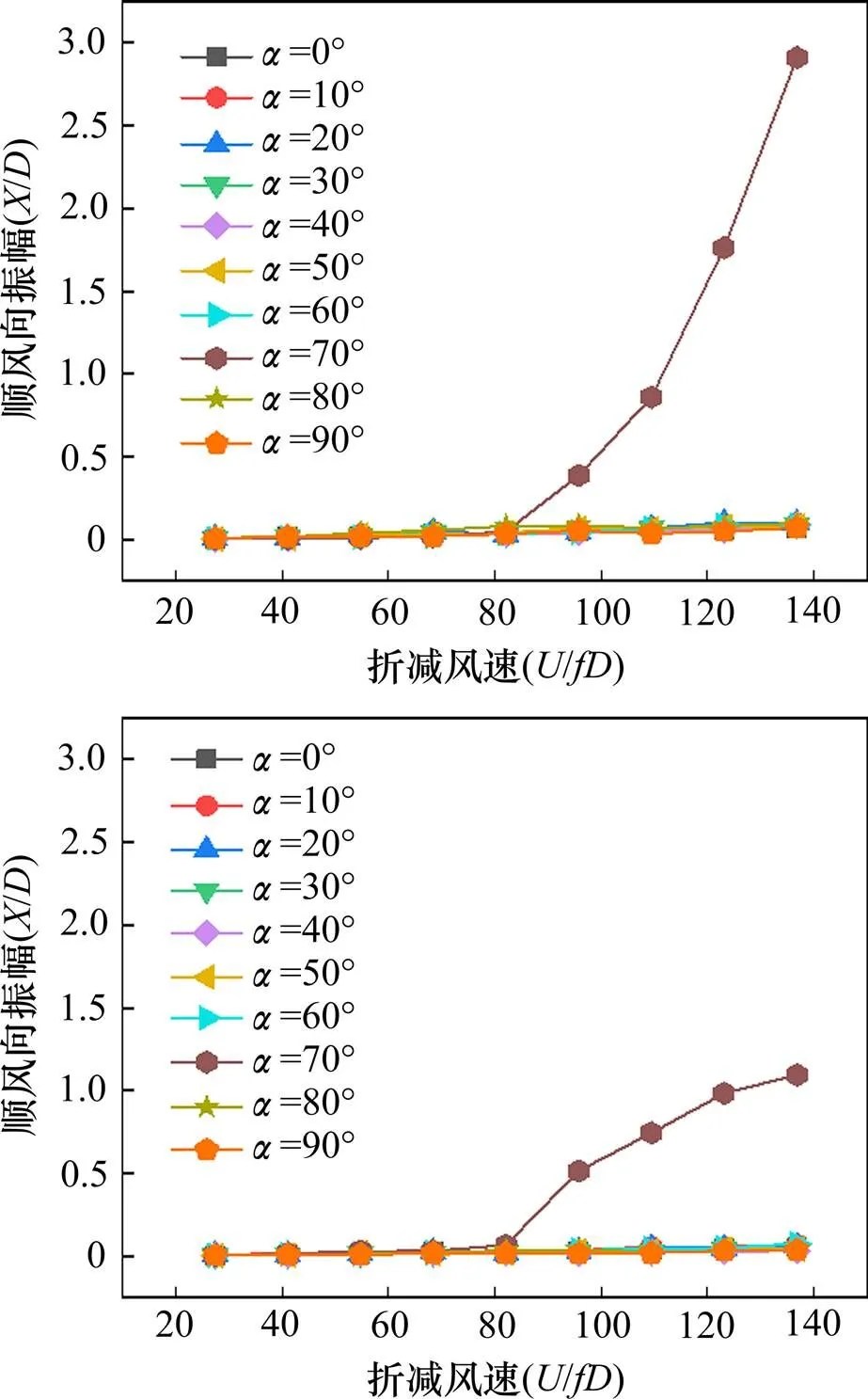
圖3 不同風攻角下粗糙尾流圓柱的振幅(ζ=0.20%)

圖4為不同風攻角下，光滑尾流圓柱的振幅隨折減風速變化曲線。其中，模型的結構阻尼比=0.24%，稍大于粗糙圓柱的值，其他試驗條件與光滑圓柱一致。結果表明，光滑圓柱在=10°與=70°時均出現明顯振動，且2個攻角下開始出現明顯振動時的折減風速均為=82。在=10°時，光滑尾流圓柱最大振幅隨折減風速增長緩慢，且振動表現為時大時小的不穩定狀態，當=137時最大振幅約為0.3。=70°時，在出現明顯振動初期(=82～108)，光滑圓柱的振幅隨風速的增長較為緩慢，且遠小于同等風速下粗糙圓柱的振幅。當折減風速=123時，光滑尾流圓柱出現大幅的振動。需要注意的是，圖4中記錄的=123時的數據點并非其穩定振幅，在試驗采集數據過程中，光滑圓柱的振幅隨時間推移不斷增大，最后超過圖3中同等折減風速下粗糙尾流圓柱的穩定振幅，并與臨近的4號圓柱(凈間距2.5)發生碰撞。

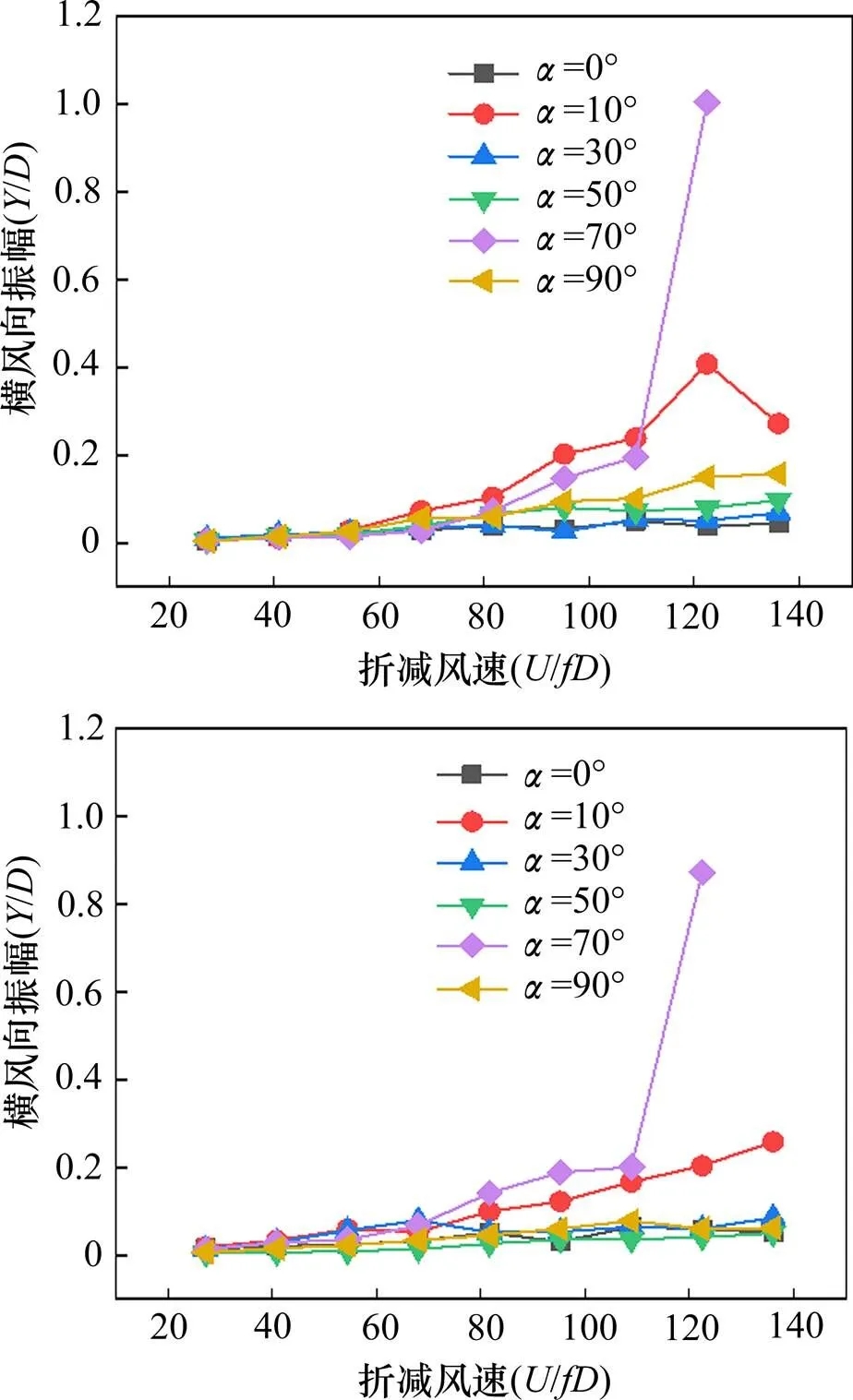
圖4 不同攻角下光滑尾流圓柱的振幅(ζ=0.24%)

2.2 振動軌跡與時程

圖5給出了70°攻角下，粗糙尾流圓柱分別在折減風速為96(觀察到穩定橢圓形振動的最小風速)和123時的振動軌跡，阻尼比為0.20%。橫坐標為順風向無量綱位移(/)，縱坐標為橫風向無量綱位移(/)，來流方向為從左向右。圖6給出了與圖5相對應的順風向和橫風向位移時程。從圖5和圖6中可以看出，粗糙圓柱起振后，在不同風速下均做順時針的橢圓形運動，橢圓形軌跡的長軸始終保持在1和3象限，這與文獻[13?15]的理論分析結果一致。另外，橢圓形運動軌跡的長軸與順風向的夾角隨著風速的增大而減小，且從圖6的位移時程可知，2個方向在不同風速下的相位差基本相同。風攻角為70°時，彈性懸掛尾流圓柱主要受4號圓柱的尾流影響。

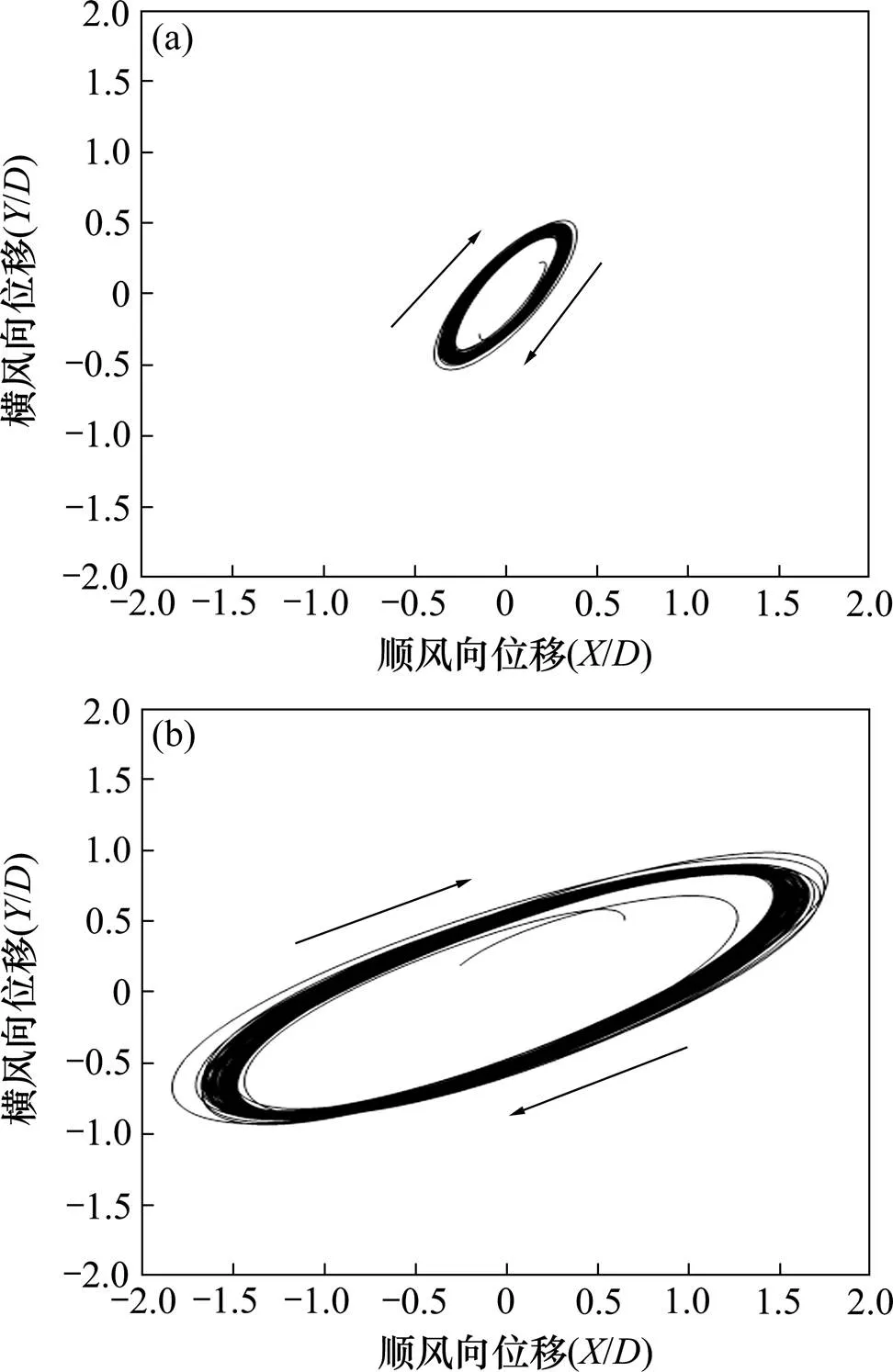
(a) U/f D=96 (Re=83 243)；(b) U/f D=123 (Re=107 030)

圖7給出了光滑尾流圓柱分別在=10°和=70°時出現大幅振動的振動軌跡，圖8給出了對應的位移時程，其中折減風速為123，阻尼比為0.24%。在10°風攻角下，彈性懸掛尾流圓柱(3號圓柱)處于1號和2號迎風圓柱的尾流中。從圖7和圖8可以看出，3號圓柱的振動軌跡不穩定，且振動軌跡為逆時針方向，這說明在10°風攻角下3號圓柱受1號圓柱的尾流影響更大。而在70°風攻角下，光滑圓柱的振動軌跡為接近直線的非常“窄”的橢圓；振動軌跡為順時針方向，與粗糙圓柱一致，長軸與順風向夾角約為45°。

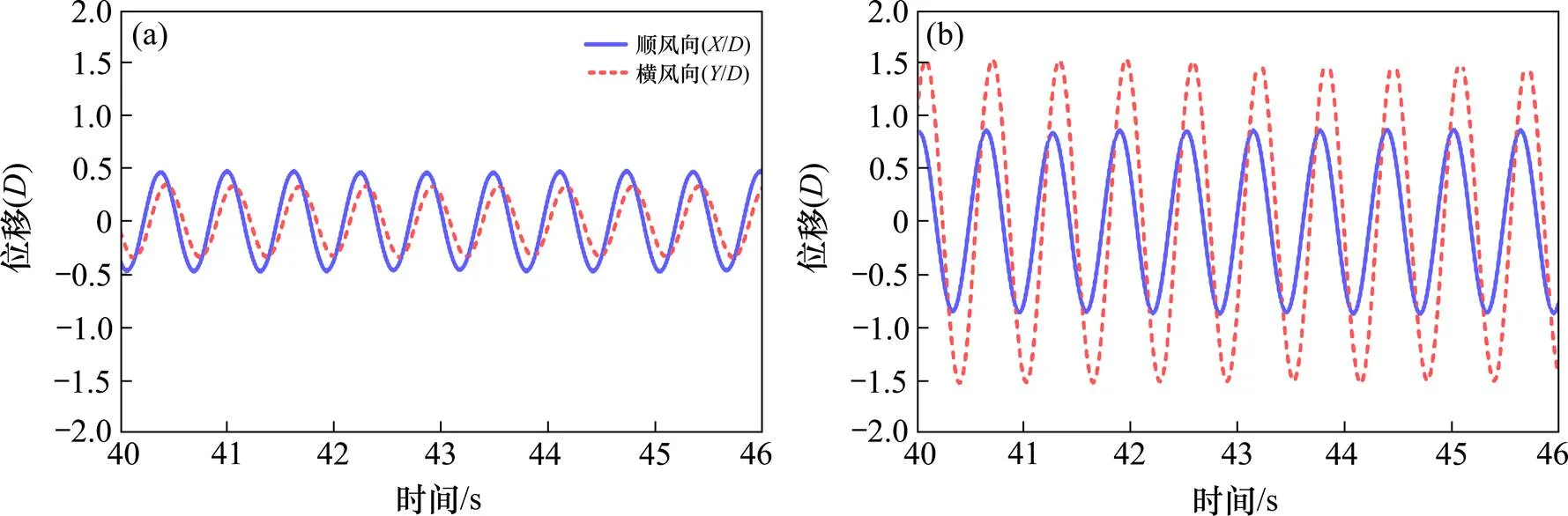
(a) U/fD=96 (Re=83 243)；(b) U/fD=123 (Re=107 030)

(a) α=10°；(b) α=70°

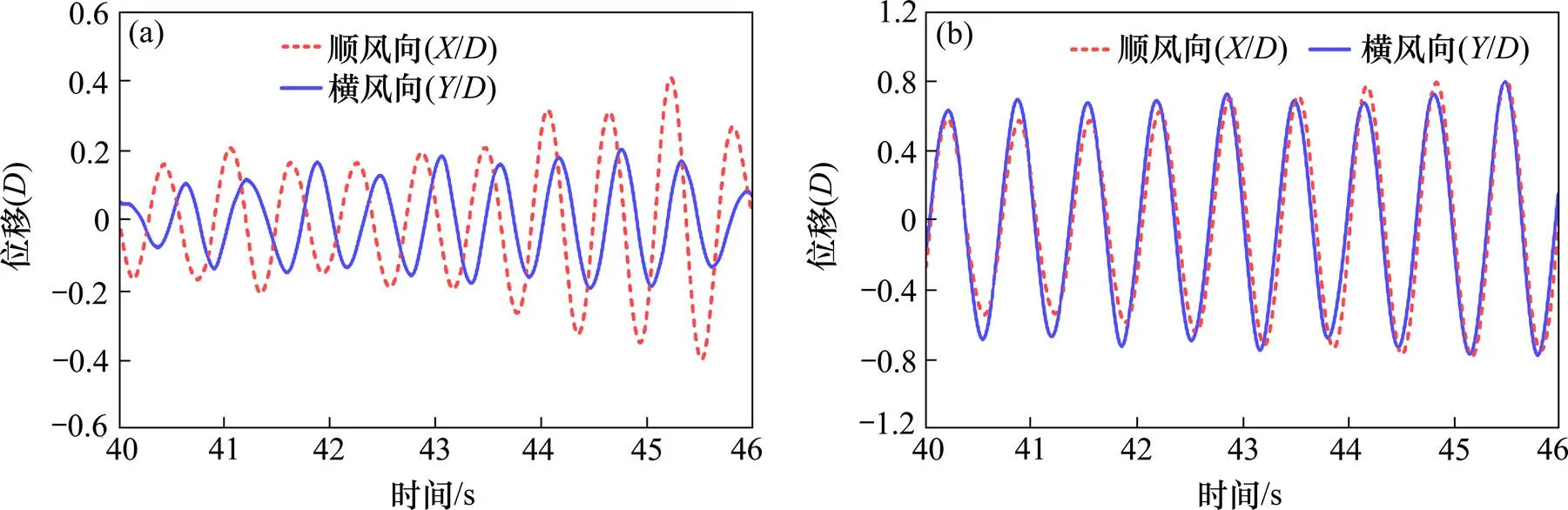
(a) α=10°；(b) α=70°

對比光滑和粗糙2種圓柱的試驗結果，可以發現，尾流圓柱發生大幅振動的最不利攻角均在70°左右，且振動軌跡均為順時針的橢圓形運動。不同的是，光滑圓柱的起振風攻角更多，且在風攻角=70°更呈現出發散狀態。

2.3 振動頻率

已有的研究結果表明[15]，尾流致振的穩定振動頻率略小于其結構頻率，氣動負剛度是尾流致振發生的主要原因。但已有文獻僅在特定風速下對上述機理進行分析。圖9給出了風攻角=70°時，彈性懸掛光滑圓柱、粗糙圓柱的穩定振動頻率隨折減風速/及雷諾數()的變化曲線。其中，方框內的數據點為出現大幅振動的工況，第1條和第2條虛線分別表示結構的順風向和橫風向的固有頻率。從圖9可以看出，當尾流圓柱發生大幅橢圓形振動時，其順風向與橫風向振動頻率相等且略小于自身結構固有頻率。表現出明顯的氣動負剛度效應。比較圖9(a)與圖9(b)，在=82時(起振風速)，2類圓柱模型的穩定振動頻率均為1.63 Hz；而當風速增大至/=123時，粗糙圓柱的穩定振動頻率為1.60 Hz，而光滑圓柱的穩定振動頻率為1.53 Hz，小于粗糙圓柱模型的值。這說明在本文的試驗工況下，平行鋼絲吊索的氣動負剛度效應比鋼絲繩吊索更加強烈。

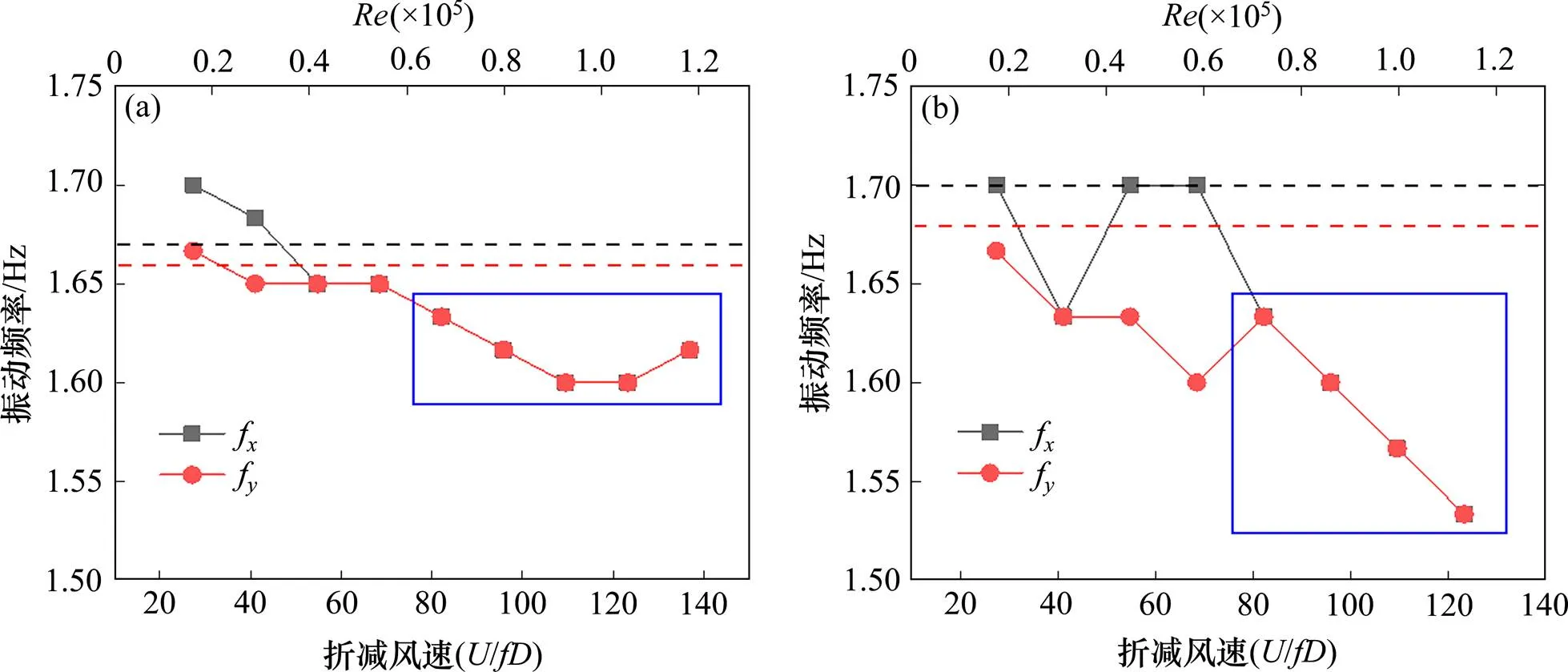
(a) 粗糙圓柱振動頻率，ζ=0.20%；(b)光滑圓柱振動頻率，ζ=0.24%

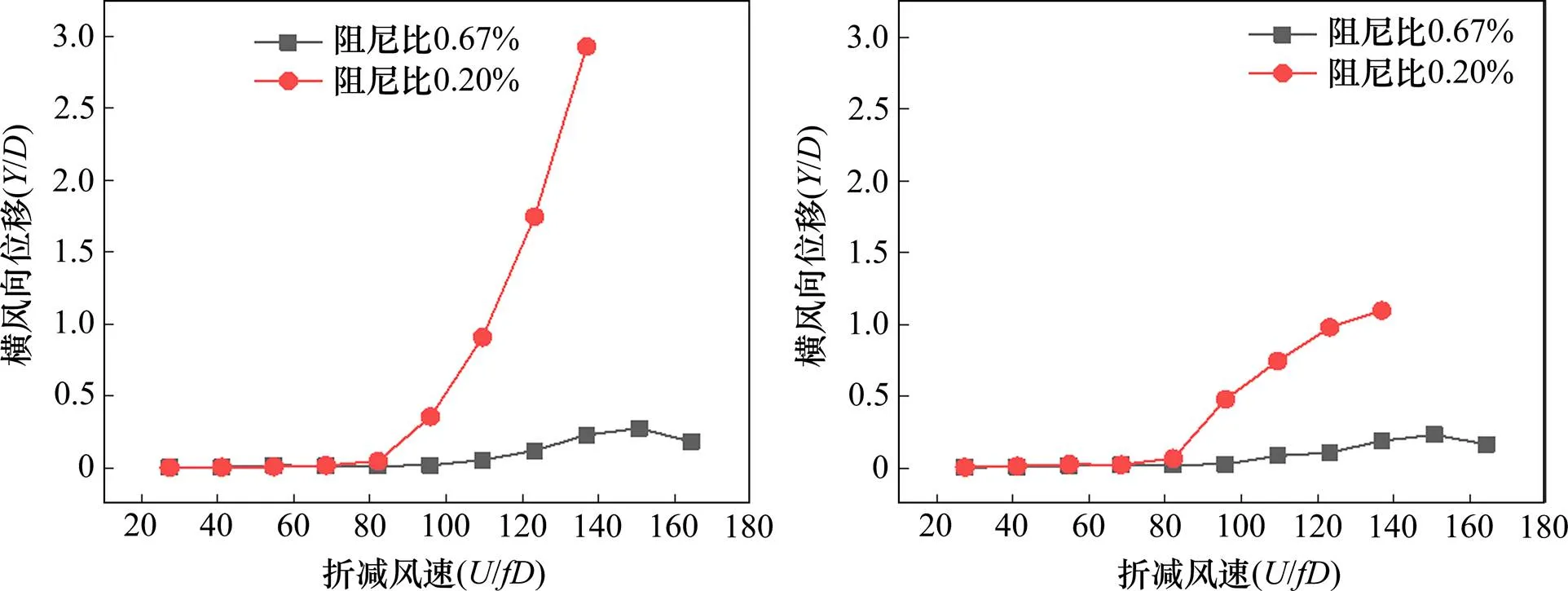
圖10 阻尼比對粗糙尾流圓柱振幅的影響(α=70°)

2.4 阻尼比影響

增大阻尼為抑制結構振動的常見方法。圖10給出了風攻角=70°時，2種阻尼比水平(0.20%和0.67%)下粗糙圓柱的順風向和橫風向振幅比較。從圖10中可以看出，在阻尼比提升至0.67%后，粗糙圓柱的尾流致振得到了很好的抑制。甚至當折減風速增大至=164(=24 m/s)的情況下，2個方向的振幅都不超過0.3。圖11給出了折減風速為/=137時尾流圓柱的振動時程。從圖11中可以看出，阻尼比較小時(如0.20%)，尾流圓柱的振動為穩定振幅，但當阻尼比增大至0.67%時，其振動形態從原來穩定的大振幅轉變為不穩定的小振幅。

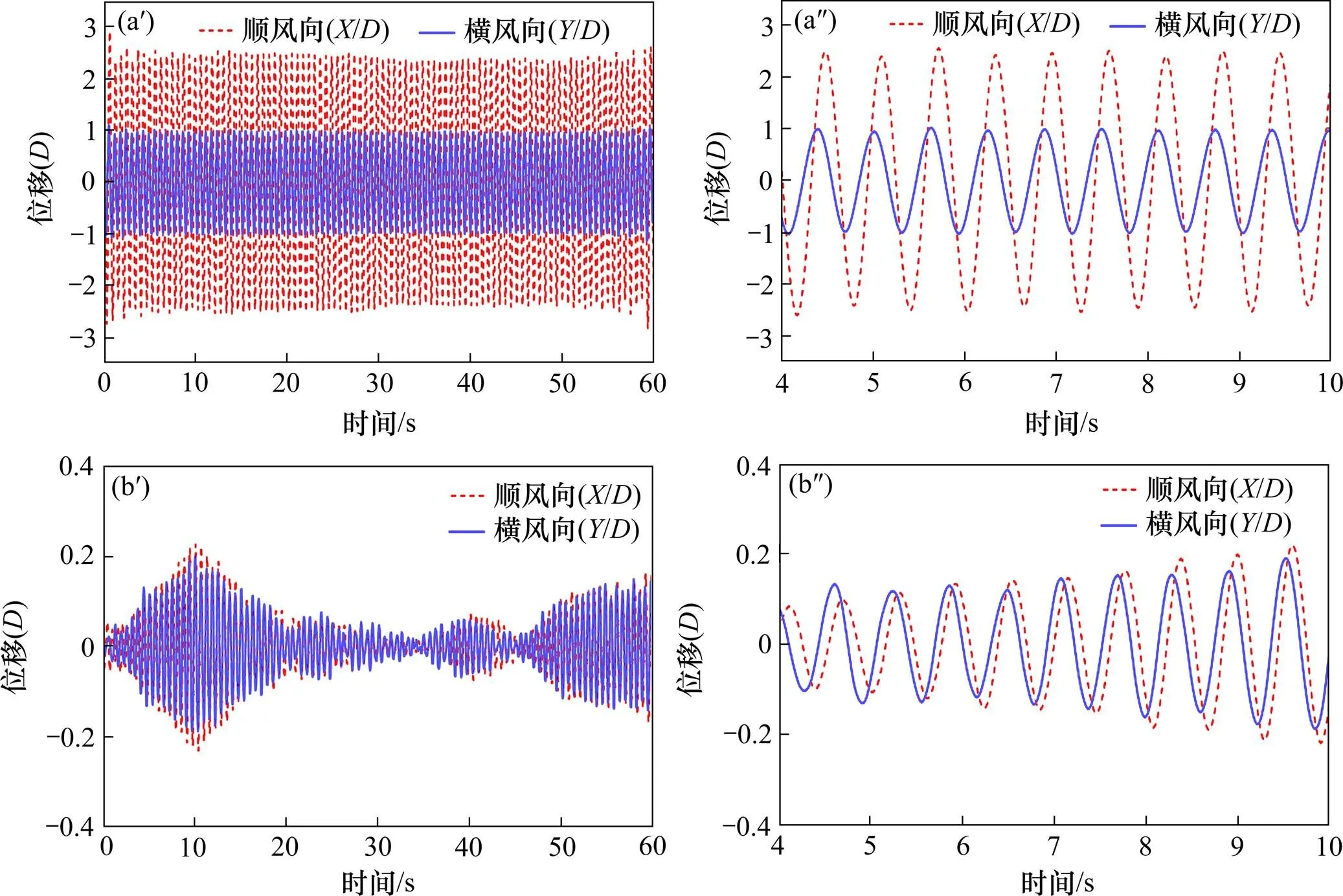
(a′)，(a″) ζ=0.20%；(b′)，(b″) ζ=0.67%

3 結論

1) 光滑和粗糙尾流圓柱發生尾流致振的最不利攻角均在70°左右；但光滑圓柱在風攻角=10°時也有較大振動，其起振風攻角范圍更寬。

2) 在70°攻角下，2類尾流圓柱的穩定振動軌跡均為順時針橢圓，但光滑尾流圓柱發生尾流致振時的氣動負剛度效應更加強烈。

3) 當阻尼比增大到0.67%時，可對粗糙圓柱的尾流致振起到很好的控制效果。

[1] Yoshimura T. Aerodynamic stability of four medium span bridges in Kyushu district[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 42(1?3): 1203?1214.

[2] Fujino Y, Kimura K, Tanaka H. Wind resistant design of bridges in Japan: developments and practices[M]. Springer Japan, New York, 2012.

[3] Laursen E, Bitsch N, Andersen J E. Analysis and mitigation of large amplitude cable vibrations at the great belt east bridge[J]. IABSE Symposium Report, 2006, 91(3): 64?71.

[4] 陳政清, 雷旭, 華旭剛, 等. 大跨度懸索橋吊索減振技術研究與應用[J]. 湖南大學學報(自然科學版), 2016, 43(1): 1?10.CHEN Zhengqing, LEI Xu, HUA Xugang, et al. Research and application of vibration control method for hanger cables in long-span suspension bridge[J]. Journal of Hunan University (Natural Science), 2016, 43(1): 1?10.

[5] Zdravkovich M M. The effects of interference between circular cylinders in cross flow[J]. Journal of Fluids and Structures, 1987: 239?261.

[6] Kitagawa T, Ohta H. Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number[J]. Journal of Fluids and Structures, 2008, 24(5): 680?699.

[7] Fujino Y, Ishihara T, Kubo Y, et al. Experimental study of wake galloping using full-scale parallel cable models for Higashi Kanjo bridge[C]// Proceedings of the 9th International symposium on Cable Dynamics, Shanghai, 2011: 191?198.

[8] Yagi T, Arima M, Araki S, et al. Investigation on wake-induced instabilities on parallel circular cylinders based on unsteady aerodynamic forces[C]// 14th International Conference on Wind Engineering-Porto Alegre. Brazil, 2015.

[9] 李永樂, 王濤, 廖海黎. 斜拉橋并列拉索尾流馳振風洞試驗研究[J]. 工程力學, 2010, 27(增1): 216?221, 227.LI Yongle, WANG Tao, LIAO Haili. Investigation on wake galloping of parallel cables in cable-stayed bridge by wind tunnel test[J]. Engineering Mechanics, 2010, 27(Suppl 1): 216?221, 227.

[10] 杜曉慶, 張利平, 劉慶寬, 等. 纜索承重橋并列索平均氣動性能的雷諾數效應[J]. 工程力學, 2017, 34(3): 189?196.DU Xiaoqing, ZHANG Liping, LIU Qingkuan, et al. Reynolds number effects on mean aerodynamic forces acting on parallel cables of cable-supported bridges[J]. Engineering Mechanics, 2017, 34(3): 189?196.

[11] 肖春云, 李壽英, 陳政清. 懸索橋雙吊索尾流馳振的失穩區間研究[J]. 中國公路學報, 2016, 29(9): 53?58, 67.XIAO Chunyun, LI Shouying, CHEN Zhengqing. Investigation on the instable region of wake galloping for twin hangers of suspension bridge[J]. China Journal of Highway and Transport, 2016, 29(9): 53?58, 67.

[12] 鄧羊晨, 李壽英, 嚴杰韜, 等. 兩類懸索橋吊索氣動穩定性比較研究[J]. 土木工程學報, 2019, 52(1): 82?88.DENG Yangchen, LI Shouying, YAN Jietao, et al. Comparation study on aerodynamic stability of two kinds of suspension bridge hangers[J]. China Civil Engineering Journal, 2019, 52(1): 82?88.

[13] LI Shouying, U T. Aerodynamic interference between the cables of the suspension bridge hanger[J]. Advances in Structural Engineering, 2019, 22(7): 1657? 1671.

[14] DENG Yangchen, LI Shouying, CHEN Zhengqing. Unsteady theoretical analysis on the wake-induced vibration of the hangers of suspension bridges[J]. Journal of Bridge Engineering, 2019, 24(2): 04018113.

[15] LI Shouying, DENG Yangchen, LEI X, et al. Wake- induced vibration of the hanger of a suspension bridge: Field measurement and theoretical modeling[J]. Structural Engineering and Mechanics, 2019, 72(2): 169? 180.

Experimental study on wake induced vibration of four-cable hangers of suspension bridges

LI Shouying1, ZHANG Mingzhe1, 2, DENG Yangchen1, 2, CHEN Zhengqing1, 2

(1. Hunan Provincial Key Lab for Wind Engineering & Bridge Engineering, Hunan University, Changsha 410082, China;2. College of Civil Engineering, Hunan University, Changsha 410082, China)

In order to study the mechanism of wake-induced vibration of four-cable hanger of long span suspension bridges, segmental cylinders with rough and smooth surfaces were adopted to respectively simulate the wire rope and parallel wire hangers. A series of wind tunnel tests were carried out to obtained the responses of wake-induced vibration of the four-cable hangers. The wind-induced vibration responses of the wake cable under different Reynolds numbers and wind attack angles were measured, and the variation law of the wake cable with the wind velocity was studied. The onset wind velocity, amplitude, trajectory, time history and vibration frequency of the wake-induced vibration of the four-cable hanger were specially studied, together with the effect of damping ratio on the wake induced vibration. The results show that the most unfavorable wind attack angle of wake-induced vibration for both smooth and rough cylinders is about 70°. But obvious large amplitude vibration of the smooth cylinder can be also found under the wind attack angle of=10°. For=70°, the stable vibration trajectories of the two types of cylinders are both clockwise ellipse. It appears that the aerodynamic negative stiffness of the smooth cylinder is stronger than that of the rough cylinder. When the damping ratio reaches 0.67%, the wake-induced vibration of the rough cylinder can be well mitigated.

four-cable hanger; wind tunnel tests;wake-induced vibration; wind angle of attack; damping ratio; vibration frequency

U441.3

A

1672 ? 7029(2020)12 ? 3118 ? 08

10.19713/j.cnki.43?1423/u.T20200097

2020?02?13

國家自然科學基金資助項目(51578234)；國家重點研發計劃項目(2017YFC0703600，2017YFC0703604)

李壽英(1977?)，男，江西萍鄉人，教授，博士，從事大跨橋梁抗風與建筑結構抗風、結構振動控制研究；E?mail：shyli@hnu.edu.cn

(編輯 陽麗霞)